آموزش ریاضی پایه هفتم
جذر و ریشه ریاضی هفتم ✖️✅ – سیر تا پیاز!
در درسنامهٔ جذر و ریشه ریاضی هفتم ریشهٔ دوم یا جذر یک عدد را تعریف میکنیم. همچنین، تعداد ریشههای دوم یک عدد را بررسی کرده و در مورد نماد رادیکال توضیح میدهیم. سعی میکنیم با حل مثالهای مختلف، به درک بهتر شما از این مبحث کمک کنیم. با ما تا انتهای درسنامه همراه باشید.
توان دوم یا مجذور
همان طور که در درسنامهٔ تعریف توان ریاضی هفتم خواندید، به توان دوم یک عدد، مجذور آن میگوییم. مثلاً، توان دوم یا همان مجذور عدد \(\Large 5\) برابر با \(\Large 5^2\) است. بنابراین، نسبت \(\Large 5^2\) با \(\Large 5\) را با عبارت “توان دوم” یا “مجذور” مشخص میکنیم. اما نسبت \(\Large 5\) با \(\Large 5^2\) را با چه عبارتی مشخص کنیم؟ در قسمت بعدی از درسنامهٔ جذر و ریشه ریاضی هفتم به این سؤال پاسخ خواهیم داد.
ریشهٔ دو یا جذر
اگر \(\Large a^2=b\) باشد، آنگاه اصطلاحاً \(\Large a\) را “ریشهٔ دوم” یا “جذر” \(\Large b\) مینامیم. با توجه به این تعریف، \(\Large 5\) ریشهٔ دوم یا همان جذر \(\Large 5^2\) است. یا مثلاً، عدد \(\Large 3\) ریشهٔ دوم (جذر) عدد \(\Large 9\) است؛ زیرا \(\Large 3^2=9\). یا به عنوان مثالی دیگر، عدد \(\Large -0.2\) جذر عدد \(\Large 0.04\) است؛ زیرا \(\Large (-0.2)^2=0.04\). از مثال اخیر میتوان فهمید که اعداد منفی نیز میتوانند ریشهٔ دوم یک عدد باشند. در قسمت بعدی از درسنامهٔ جذر و ریشه ریاضی هفتم به بررسی تعداد ریشههای دوم اعداد میپردازیم.
تعداد ریشههای دوم اعداد
به طور کلی، تعداد ریشههای دوم هر عدد، بسته به اینکه مثبت، منفی و یا صفر باشد، متفاوت است. بر این اساس میتوان دسته بندی زیر را انجام داد:
- هر عدد مثبت، دو ریشهٔ دوم دارد.
- عدد \(\Large 0\) تنها یک ریشهٔ دوم دارد.
- اعداد منفی، ریشهٔ دوم ندارند.
اینکه چرا اعداد منفی، ریشهٔ دوم ندارند، روشن است؛ زیرا هر عددی را چه مثبت باشد و چه منفی، اگر به توان \(\Large 2\) برسانیم، مثبت خواهد شد. بنابراین هیچ عددی نیست که اگر به توان \(\Large 2\) برسد، منفی شود. بنابراین، اعداد منفی، ریشهٔ دوم ندارند. در مورد \(\Large 0\) هم که واضح است؛ تنها عددی که توان دوم آن برابر با \(\Large 0\) میشود، خود \(\Large 0\) است. اما ریشههای دوم اعداد مثبت، نیاز به بررسی بیشتر دارند. در قسمت بعدی از درسنامهٔ جذر و ریشه ریاضی هفتم به ریشههای دوم اعداد مثبت میپردازیم.
برای علاقهمندان: تمام آنچه که در مورد تعداد ریشههای دوم گفتیم، در مجموعهٔ اعداد حقیقی صادق است. با اعداد حقیقی در درسنامهٔ اعداد حقیقی ریاضی نهم آشنا خواهید شد. آنچه که گفتیم، برای دورهٔ دبیرستان صادق و کافی است. اما به طور کلی در ریاضیات میتوان ریشهٔ دوم اعداد منفی را در میدان اعداد مختلط یافت. در صورتی که مایلید، در مورد اعداد مختلط مطالعه کنید.
ریشههای دوم اعداد مثبت و نماد رادیکال
هر عدد مثبتی، دو ریشهٔ دوم دارد. یک ریشهٔ مثبت و یک ریشهٔ منفی که قرینهٔ یکدیگر هستند. به طور مثال، اعداد \(\Large 6\) و \(\Large -6\)، ریشههای دوم عدد \(\Large 36\) هستند. ریشهٔ دوم مثبت یک عدد را با استفاده از علامت \(\Large \sqrt{}\) نشان میدهیم. به علامت \(\Large \sqrt{}\) رادیکال میگوییم. مثلاً، \(\Large \sqrt{9}\) ریشهٔ دوم \(\Large 3\) است. یا به طور مثال، \(\Large \sqrt{25}\) که همان \(\Large 5\) است، ریشهٔ دوم عدد \(\Large 25\) است. بنابراین، با استفاده از نماد رادیکال، میتوانیم ریشههای دوم یک عدد مثبت مانند \(\Large a\) را با \(\Large \sqrt{a}\) و \(\Large -\sqrt{a}\) نشان دهیم. مثلاً، اعداد \(\Large \sqrt{49}\) و \(\Large -\sqrt{49}\) که همان اعداد \(\Large 7\) و \(\Large -7\) هستند، ریشههای دوم عدد \(\Large 49\) هستند.پس هر عدد مثبت دو ریشه دارد ولی با توجه به تعریف وقتی می نویسیم \(\Large \sqrt{a}\) منظور ما ریشه مثبت \(\Large a\) است .در جدول زیر، ریشههای دوم چند عدد را نشان دادهایم.
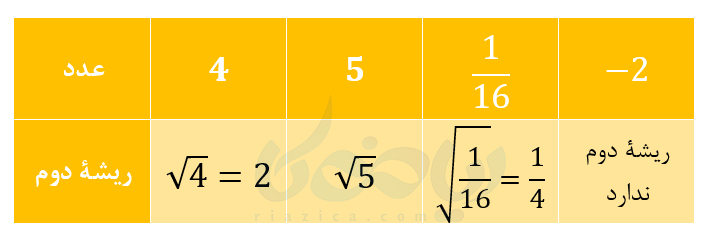
مثال از درسنامهٔ جذر و ریشه ریاضی هفتم
مثال 1: مقدار \(\Large \sqrt{\frac{1}{16}}\) و \(\Large \sqrt{\frac{16}{49}}\) را به دست آورید.
حل: همان طور که گفتیم، منظور از علامت رادیکال، ریشهٔ دوم مثبت یک عدد است. اگر \(\Large \frac{1}{4}\) را دوبار در خودش ضرب کنیم، \(\Large \frac{1}{16}\) حاصل خواهد شد. بنابراین \(\Large \sqrt{\frac{1}{16}}=\frac{1}{4}\). دقت کنید، \(\Large -\frac{1}{4}\) جواب \(\Large \sqrt{\frac{1}{16}}\) نیست. درست است که \(\Large -\frac{1}{4}\) ریشهٔ دوم \(\Large \frac{1}{16}\) است، اما همان طور که گفتیم، وقتی از علامت رادیکال استفاده میکنیم، منظورمان ریشهٔ دوم مثبت یک عدد است. بنابراین هیچگاه جواب رادیکال منفی نخواهد شد. البته در آینده، ریشههای سوم و دیگر ریشه ها را خواهید آموخت که در آنجا منظور از علامت رادیکال متفاوت خواهد بود.
در مورد \(\Large \sqrt{\frac{16}{49}}\)، پاسخ برابر با \(\Large \frac{4}{7}\) خواهد شد. زیرا داریم:
\(\LARGE (\frac{4}{7})^2=\frac{4}{7} \times \frac{4}{7}=\frac{16}{49}\)
\(\LARGE \Rightarrow \sqrt{\frac{16}{49}}=\frac{4}{7} \)
در سال آینده در درسنامهٔ خواص ضرب و تقسیم رادیکالها با ضرب رادیکالها و نحوهٔ محاسبهٔ آنها بیشتر آشنا خواهید شد. اما فعلاً میتوانید با توجه به تعریف رادیکال، پاسخ مسائل ساده را به دست آورید.
مثال از درسنامهٔ جذر و ریشه ریاضی هفتم
مثال 2: مقدار \(\Large \sqrt{-16}\) را به دست آورید؟
حل: همان طور که گفتیم، اعداد منفی، ریشهٔ دوم ندارند. بنابراین مقدار خواسته شده توسط مسئله وجود ندارد.
مثال از درسنامهٔ جذر و ریشه ریاضی هفتم
مثال 3: مقدار \(\Large \sqrt{43}\) بین کدام دو عدد طبیعی قرار میگیرد؟
حل: مقدار \(\Large \sqrt{43}\) برابر با عدد مثبتی است که اگر به توان \(\Large 2\) برسد، برابر با \(\Large 43\) خواهد شد. از آنجاییکه \(\Large 6^2=36\) و \(\Large 7^2=49\) است و عدد \(\Large 43\) بین \(\Large 36\) و \(\Large 49\) قرار دارد، میتوان حدس زد که \(\Large \sqrt{43}\) بین دو عدد \(\Large 6\) و \(\Large 7\) قرار دارد. یعنی داریم:
\(\LARGE 6<\sqrt{43}<7\)
مثال از درسنامهٔ جذر و ریشه ریاضی هفتم
مثال 4: مساحت قسمت سبز رنگ در شکل زیر را به دست آورید.
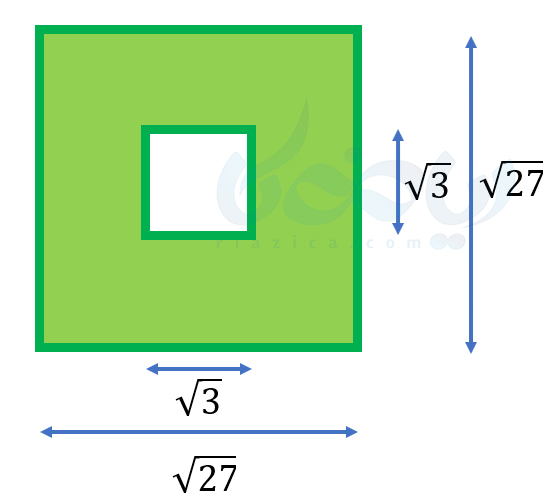
حل: کافی است مساحت مربع بزرگ و کوچک را به دست آورده و تفاضلشان را محاسبه کنیم. اگر مساحت مربع بزگرتر را با \(\Large S_l\) و مساحت مربع کوچکتر را با \(\Large S_s\) نشان دهیم، داریم:
\(\LARGE S_l= \sqrt{27} \times \sqrt{27}\)
\(\LARGE S_s= \sqrt{3} \times \sqrt{3}\)
توان دوم ریشهٔ دوم یک عدد، برابر با خود عدد میشود. بنابراین اگر یک رادیکال را در خودش ضرب کنیم، حاصل برابر با عدد زیر رادیکال خواهد شد. بنابراین داریم:
\(\LARGE S_l= \sqrt{27} \times \sqrt{27}=27\)
\(\LARGE S_s= \sqrt{3} \times \sqrt{3}=3\)
\(\LARGE \Rightarrow S_l-S_s=27-3=24\)
بنابراین، مساحت قسمت هاشورخورده برابر با \(\Large 24\) است.
برای یادگیری جذر تقریبی به پست جذر تقریبی هشتم مراجعه کنید.همچنین توصیه می شود پستهای تعریف توان و محاسبه اعداد تواندار و ساده کردن عبارتهای تواندار رو قبلش مطالعه کنید
زنگ آخر کلاس جذر و ریشه ریاضی هفتم
در درسنامهای که از ریاضی هفتم خواندیم، با ریشهٔ دوم یا همان جذر آشنا شدیم. دیدیم که اعداد مثبت دارای دو ریشه هستند و این دو ریشه قرینهٔ یکدیگرند. همان طور که گفتیم، برای نشان دادن ریشهٔ دوم مثبت اعداد از علامت رادیکال استفاده میکنیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با جذر و ریشه ریاضی هفتم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





خیلی عالی بود من توایناواقعا مشکل داشتم برام جا افتاد?
با سلام وقت به خیر
خدا رو شاکریم که تونستیم در راه تعلیم دانش آموزان عزیز کشورمون قدمی برداریم
خوب بود مخصوصا سوالاتتون ?
با سلام وادب
ممنون از نظر شما
سلام خسته نباشید خلیی خوب بود
سلام ممنون از انرژی که به ما میدهید بزای ادامه کار
عالی
عالی بود
واقعا کامل و درست بود ?
ممنون ?????
با سلام
ممنون از لطف شما
عالی تشکر
ولی کاشکی راجبه جذر تقریبی بیشتر توضیح میدادید
سلام دوست عزیز در این پست گفته شدهhttps://riazica.com/approximate-square-root/
عالییی بود
میشه بگید چرا جذر عدد رادیکال ۹ برابر ۳نیست
میشه بگید چرا جذر عدد رادیکال ۹ برابر ۳نیست
با سلام
جذرش ۳ هست ولی ریشه های دومش مثبت ومنفی ۳ میشه چون هر دو اگه به توان دو برسن میشن نه
سلام خسته نباشید
در بالا گفته بودین ها رادیکال هارو در یکدیگر ضرب کنیم همان عدد میشود آیا در جمع و منفی هم همان کار انجام میگردد؟؟؟؟؟
با سلام وادب
خیر
عالی
سلام واقعا از زحماتتون متشکرم خیلی خوب و عالی بود??
فقط آگه میشه جذر تقریبی روبیشتر توضیح بدید ممنون میشم??
با سلام وادب
در مطالب پایه هشتم ونهم توضیح دادیم
توم مث من صبح روز امتحان داری میخونی ?
سلام دوست عزیز میتونید در این پست جذر تقریبی رو یاد بگیرید.https://riazica.com/approximate-square-root/
سلام
عالین
من واقعا ب خوبی یاد گرفتم درحالی ک وقتی معلم میگف نمی فهمیدم اما باخوندن اینا درست یادگرفتم
و این سوالات رو هم ک گذاشتید عالی بودن;-)
با سلام وادب
ممنون از انرژی که به ما می دهید.
عالیه ??
سپاس دوست عزیز
از نظر من مطالب خیلی عالی بود ??
سپاس از دیدگاه شما
خیلی خیلی خیلی خوب بود
عالی بود😊❤
فقط کاش در مورد سوال آخر که شکل داشت بیشتر توضیح می دادید 🙏🏻
سلام خیلی آموزش خوبی دا شت ممنون 👌👌👌👌👌👌👌👍👍👍کجا می تونم روش جزر تقریبی را هم مطالعه کنیم
سلام دوست عزیز به لینک زیر مراجعه کنید
https://riazica.com/approximate-square-root/
سلام خسته نباشید خیلی عالی بود ممنون
کاش نمونه سوال هم داشتید به همراه پاسخنامه
با سلام وادب
با حمایت دوستان انشاالله در آینده قرار میدهیم
خیلی توضیحات کامله مرسی 🌟
اگر تو ساده کردن پایه و توان برابر نبود چیکار کنیم؟
با سلام اگهاصلا نشه برابرشون کرد فقط میشه مقدار بدست آورد
ذکات علم نشر آن است .سپاس از امور خیریه شما استاد عزیز
عالی بود
ممنون دوست عزیز
ممنون
من واقعا هیچی متوجه ۳
با سلام
دقیقا کجاش رو متوجه نشدید؟
همه جاش
پس مشکل از خودتونه
ممنون از لطفتون عالی بود
خوشحالیم که مفید واقع شده
علی بود
میشه لطفا جذر دقیق عدد47 رو بدست بیارین
عالی بود
میشه لطفا جذر دقیق عدد47 رو بدست بیارین