آموزش ریاضی پایه هشتم
خط و دایره : از سیر ➖ تا پیاز 🔴
اردیبهشت
خب من که هم خط رو می‌شناسم، هم دایره رو! پس چی می‌تونه باشه این درس؟؟؟ در این درس‌نامه از دسته آموزش ریاضی پایه هشتم به آموزش تعریف ریاضی دایره، وضعیت‌های خط و دایره نسبت به هم، تعریف خط مماس بر دایره، بررسی ویژگی‌های خط مماس، تعریف وتر و بررسی مثلث‌هایی که یکی از اضلاع آن، خط مماس است می‌پردازیم و با حل چندین مثال به این مبحث مسلط می‌شویم.
تعریف دایره
به مجموعه نقاطی از صفحه که فاصله همه این نقاط از یک نقطه مشخص، به یک اندازه باشد، دایره گفته می‌شود.
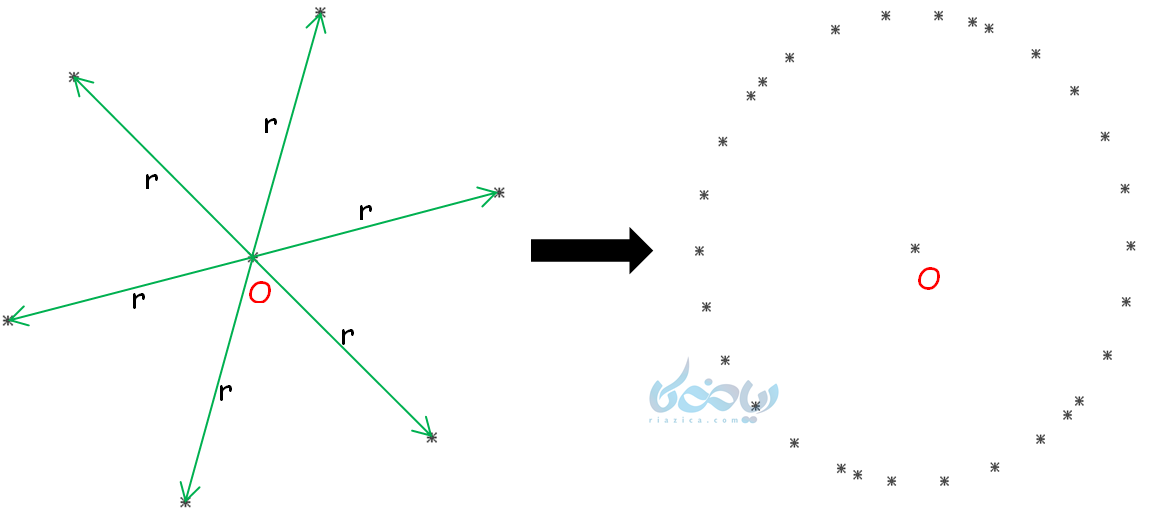
این نقطه مشخص، مرکز دایره \( \Large \ (O) \) و آن فاصله ثابت، شعاع دایره \( \Large \ (r) \) نامیده می‌شود.
یکی از کاربردهای اساسی دایره، در مبحث مثلثات است که تحت عنوان دایره واحد (مربوط به کتاب ریاضی دهم) بطور مفصل توضیح داده شده است.
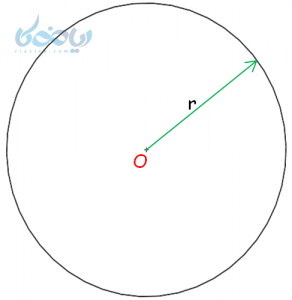
نکته: دایره‌ای به مرکز نقطه \( \Large \ O \) و شعاع \(\Large \ r \) را به اختصار بصورت \(\Large \ C(O,r) \) نشان می‌دهند. بنابراین \(\Large \ C(M,4) \) یعنی دایره‌ای به مرکز نقطه \(\Large \ M \) و شعاع 4.
وضعیت خط و دایره
یک خط و دایره می‌توانند نسبت به هم سه وضعیت مختلف داشته باشند:
الف) خط، دایره را در هیچ نقطه‌ای قطع نکند.
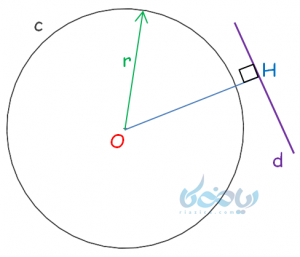
در این حالت، فاصله خط تا مرکز دایره (\(\Large \ \overline{OH} \)) از شعاع دایره \(\Large \ (r) \) بیشتر است: (\(\Large \ r<\overline{OH} \)).
نکته: فاصله خط تا یک نقطه، کوتاهترین فاصله آن‌هاست؛ به عبارتی برابر است با طول پاره خط عمود بین نقطه و خط.
ب) خط، دایره را در دو نقطه قطع کند.
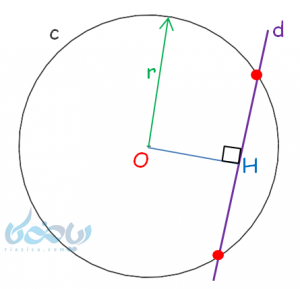
در این حالت، فاصله خط تا مرکز دایره (\(\Large \ \overline{OH} \)) از شعاع دایره \(\Large \ (r) \) کمتر است: (\(\Large \ r>\overline{OH} \)).
مثال 1: خط \(\Large \ d \)، دایره \(\Large \ c \) را در چند نقطه قطع میکند؟
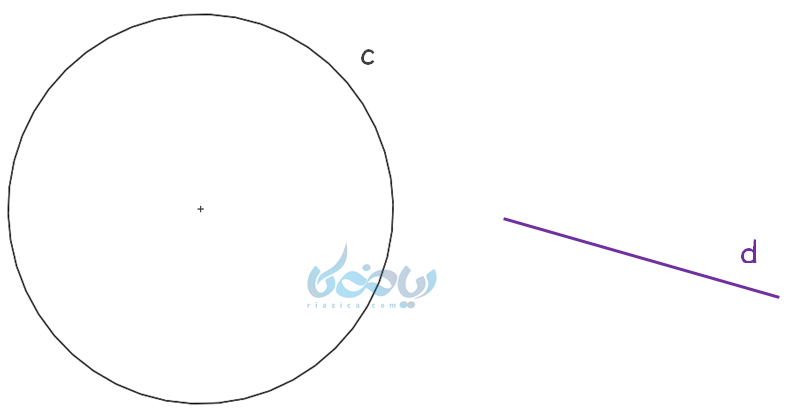
حل 1:
آیا پاسخ شما این بود که با توجه به شکل، خط دایره را قطع نمیکند؟
باید بگویم پاسخ صحیح نیست! اگر خط را امتداد دهید، خواهید دید که دایره را در دو نقطه قطع میکند.
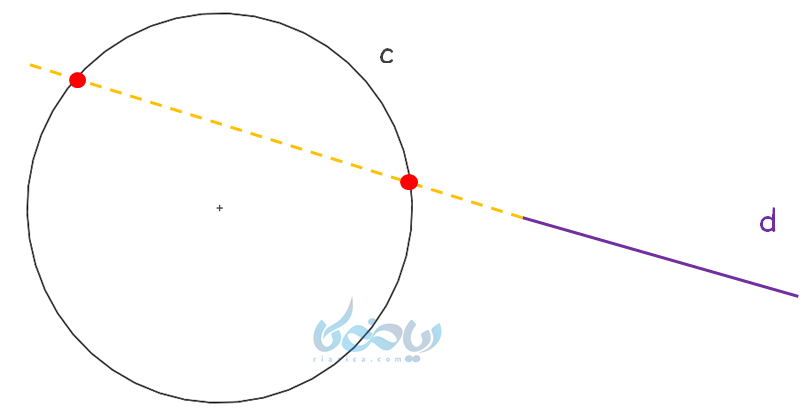
بنابراین:
نکته: در تعیین وضعیت خط و دایره نسبت به هم، باید خط را آن‌قدر امتداد داد تا نقاط برخورد در صورت وجود مشخص شوند.
ج) خط، دایره را تنها در یک نقطه قطع کند.
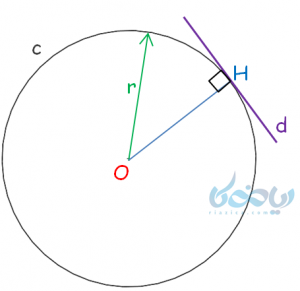
در این حالت، فاصله خط تا مرکز دایره (\(\Large \ \overline{OH} \)) برابر با شعاع دایره \(\Large \ (r) \) است: (\(\Large \ r=\overline{OH} \)). این حالت، در هندسه بسیار پرکاربرد است که در بخش بعد با آن بیشتر آشنا می‌شویم.
مثال 2: فاصله خطی تا مرکز دایره برابر با \(\Large\ \frac{2}{5}r \) است. خط و دایره چه وضعیتی نسبت به یکدیگر دارند؟
حل 2:
از آنجا که فاصله خط تا دایره از شعاع کمتر است (\(\Large \ \overline{OH}=\frac{2}{5}r<r \))، بنابراین خط در دو نقطه دایره را قطع میکند.
خط مماس بر دایره
تعریف خط مماس بر دایره
خطی که دایره را تنها در یک نقطه (نقطه تماس) قطع کند، خط مماس بر دایره نامیده می‌شود.
ویژگی‌های خط مماس
خط مماس بر دایره، ویژگی‌های منحصربفردی در ریاضیات دارد که در ادامه می‌بینیم:
- شعاع دایره در نقطه تماس بر خط مماس عمود است.
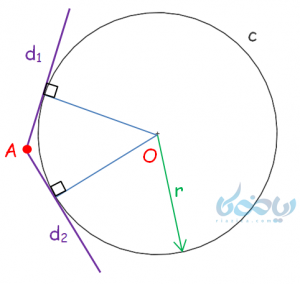
- از هر نقطه خارج دایره می‌توان 2 خط مماس بر دایره رسم کرد؛ به عنوان مثال در شکل زیر، از نقطه \(\Large \ A \) دو مماس بر دایره \(\Large \ C(O,r) \) رسم شده است.
مثال 3: زاویه خواسته شده در شکل زیر را پیدا کنید؟
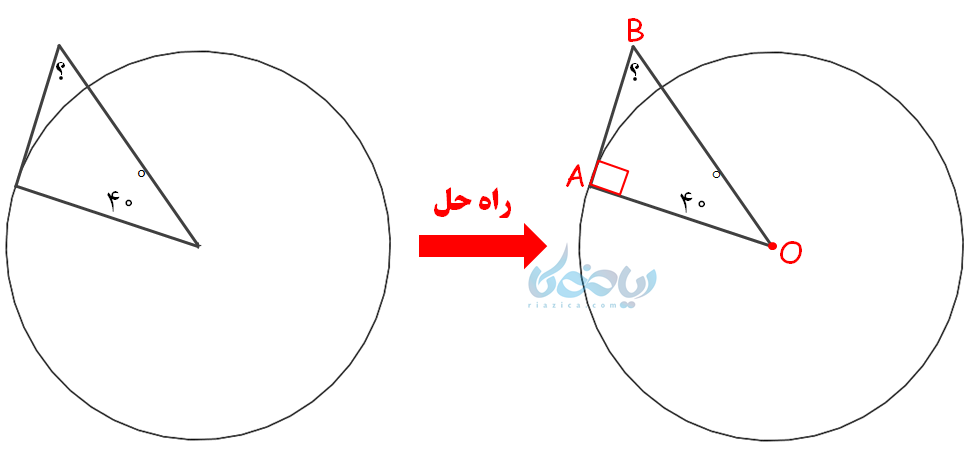
حل 3:
مثلثی داریم که در صورت سؤال، تنها اندازه یک زاویه از آن داده شده است.
با دقت به وضعیت خط و دایره، مشاهده می‌کنیم که پاره خط \(\Large \ \overline{AB} \) بر دایره در نقطه A مماس است؛ بنابراین طبق ویژگی خط مماس، این پاره خط در نقطه A بر شعاع دایره (پاره خط \(\Large \ \overline{OA} \)) عمود است، پس زاویه \(\Large \ \hat A \) قائمه است.
از سویی می‌دانیم مجموع زوایای داخلی مثلث، برابر با °180 است؛ بنابراین:
\(\Large \ \hat A + \hat O + \hat B = 180° \)
\(\Large \ → 90+40+ \hat B = 180 \)
\(\Large \ → \hat B =180- (90+40)= 50° \)
مثال 4: در شکل زیر، خطوط \(\Large \ a \) و \(\Large \ b \) موازیند. اندازه زاویه \(\Large \ \hat M \) را بدست آورید؟
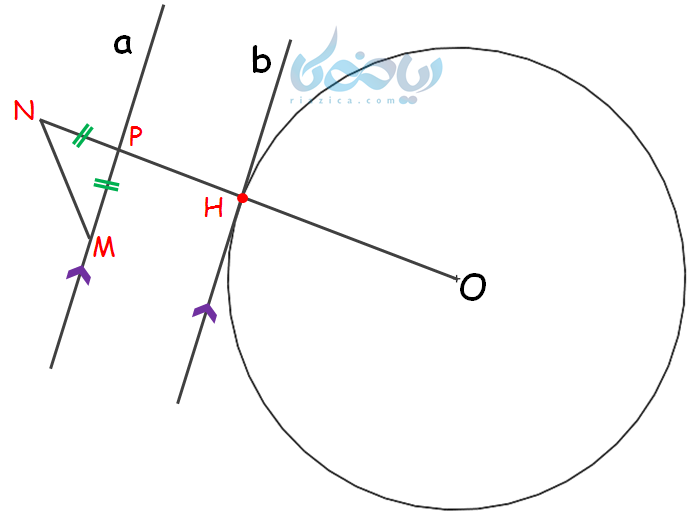
حل 4:
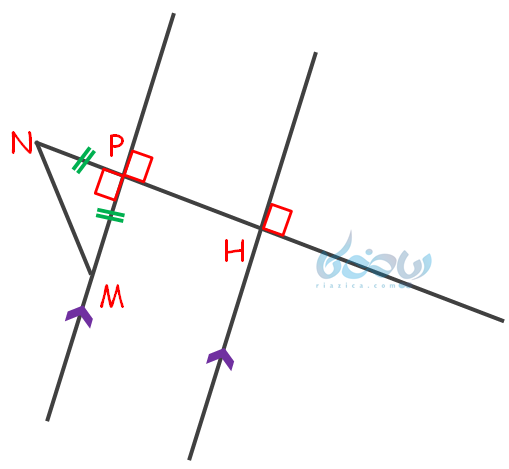
- می‌دانیم که خط b تنها دایره را در یک نقطه قطع کرده است، پس خط مماس بر دایره است.
- می‌دانیم شعاع دایره در نقطه تماس بر خط مماس عمود است؛ بنابراین خط رسم شده از مرکز دایره \(\Large \ (O) \) به نقطه تماس \(\Large \ (H) \) بر خط b عمود است.
- با توجه به موازی بودن خطوط a و b، می‌توان قائمه بودن زاویه \(\Large \ \hat P \) را نتیجه گرفت؛ چون خطی که دو خط موازی را قطع کند با آن‌ها زاویه‌های مساوی می‌سازد (یادآوری: خطوط موازی ومورب).
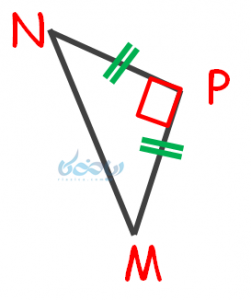
در مثلث قائم‌الزاویه \(\Large \ PMN \)، دو ضلع برابرند؛ بنابراین این مثلث متساوی الساقین بوده و دارای یک زاویه قائمه و دو زاویه برابر است. پس:
\(\Large \ \hat P + \hat M + \hat N = 180° \)
\(\Large \ →90+2 \hat M =180 \)
\(\Large \ → 2 \hat M= 180-90=90\)
\( \Large \ →\hat M= 45° \)
وتر ؛ یک نمونه جذاب از مبحث خط و دایره
تعریف وتر
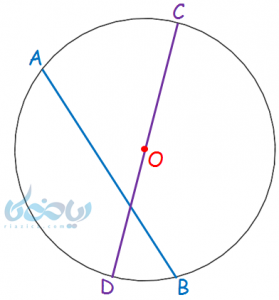
پاره‌خطی است که دو نقطه روی محیط دایره را به یکدیگر وصل میکند و با دو حرف نشان داده می‌شود. مانند وتر \(\Large \ AB \) در شکل زیر، که پاره‌خط بین دو نقطه \(\Large \ A \) و \(\Large \ B \) روی محیط دایره است.
ویژگی‌های وتر
وتر دایره، تعدادی ویژگی دارد که به شرح زیر می‌باشد:
- دایره دارای تعداد بی‌شماری وتر است.
- بزرگترین وتر دایره، وتری است که از مرکز دایره عبور میکند و قطر نام دارد. (مانند قطر \(\Large \ CD \) در شکل)
- دایره دارای تعداد بی‌شماری قطر است.
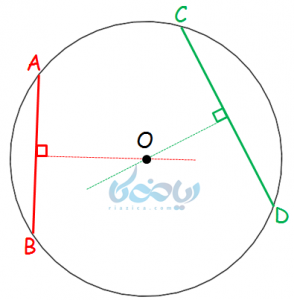
- فاصله هر وتر تا مرکز دایره، عمود منصّف آن وتر است. (به عبارت دیگر، پاره‌خطی که از مرکز دایره بر یک وتر عمود می‌شود، آن وتر را نصف میکند.
- برای پیدا کردن مرکز یک دایره، کافی است عمود منصّف دو وتر غیر موازی را رسم کرده و امتداد دهید. نقطه تقاطع این دو عمود منصّف، مرکز دایره خواهد بود.
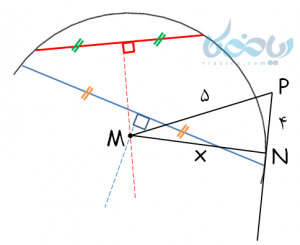
مثال 5: در دایره ناقص زیر، مقدار \(\Large \ x \) را بدست آورید.
حل 5:
توجه شود که در این دایره ناقص، دو وتر رسم شده است و عمود منصّف هر یک از این وترها نیز رسم شده است. همان‌طور که یاد گرفتیم، محل تقاطع عمود منصّف‌های وترهای دایره، مرکز دایره است. بنابراین نقطه \(\Large \ M \) مرکز دایره است.
از طرفی مشاهده می‌شود که خط شامل پاره‌خط \(\Large \ PN \)، تنها دایره را در یک نقطه قطع کرده و بنابراین، مماس بر دایره است.
پس \(\Large \ MN \) شعاع دایره است و بر خط مماس عمود است، بنابراین زاویه \(\Large \ \hat N \) قائمه و مثلث \(\Large \ PNM \) قائم‌الزاویه است.
حال برای یافتن \(\Large \ x \) کافی است از رابطه فیثاغورس استفاده کنیم:
\(\Large \ x^2 + 4^2 = 5^2 \)
\(\Large \ → x^2 = 25 – 16 = 9 \)
\(\Large \ → x = 3 \)
اثبات ویژگی شماره 4 از ویژگی‌های وتر
قبلاً گفته شد که فاصله یک نقطه تا یک خط، پاره‌خطی است که از نقطه بر خط عمود می‌شود. بنابراین برای این که ویژگی 4 را اثبات کنیم باید پاره‌خطی از مرکز دایره \(\Large \ (O) \) بر وتر \(\Large \ (\overline {AB}) \)عمود کرده \(\Large \ (\overline {OH}) \) و سپس بررسی کنیم که آیا این پاره‌خط، وتر را نصف میکند یا خیر؟
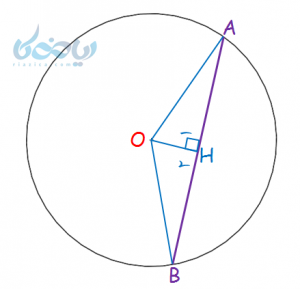
مشاهده می‌شود که مثلث‌های \(\Large \ AOH \) و \(\Large \ BOH \) که هر دو قائم‌الزاویه هستند (چون پاره‌خط بر وتر عمود است) به حالت وتر و یک ضلع (و ض) هم‌نهشت هستند (یادآوری: فصل ششم، درس چهارم کتاب درسی)؛ چون:
الف) برابری وترهای دو مثلث: \(\Large \ (\overline {OA} = \overline {OB}) \) ؛ چون هر دو شعاع دایره‌اند.
ب) برابری یک ضلع: ضلع \(\Large \ \overline {OH} \) در هر دو مشترک است.
از هم‌نهشتی این دو مثلث نتیجه می‌شود که: \(\Large \ \overline {OH} = \overline {BH} \) (یعنی پاره‌خط \( (r) \)، وتر را نصف کرده است).
بنابراین پاره‌خط \(\Large \ OH \)، عمود منصّف وتر \(\Large \ AB \) می‌باشد.
ویدیو آموزش مبحث خط و دایره
در این ویدیو مبحث خط ودایره فصل نهم کتاب ریاضی هشتم یه طور کامل با مثالهای متعدد تدریس شده
زنگ آخر
در این درس، تعریف ریاضی دایره به عنوان مجموعه نقاط، وضعیت‌های سه‌گانه خط و دایره، ویژگی‌های خط مماس، تعریف وتر و ویژگی‌های آن و نحوه پیدا کردن مرکز دایره به کمک وتر را یاد گرفتیم. همچنین مثالهای مختلفی از این مباحث و نیز ترکیب آن‌ها با هم را مورد بررسی قرار دادیم. با در نظر داشتن همین چند نکته می‌توانیم به مسائلی که در این باره مطرح می‌شود، پاسخ بدهیم.
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاه‌ها برایمان بنویسید. کارشناسان ریاضیکا به سوالات شما پاسخ خواهند داد.
ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی هشتم به شما پیشنهاد می‌دهیم:
- زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعیها!
- اعداد صحیح ↔️➖➕– نمایش روی محور مختصات
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعیها!
- تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
- عدد اول ریاضی هشتم 1️⃣👨🎓 – کاملترین آموزشی که لازم داشتید.
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- خط و دایره : از سیر ➖ تا پیاز 🔴
- خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خط‌ها در چهارراه زاویه!
- چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!
- ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
- فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارتهای جبری استفاده کن!
- حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
- بردار و مختصات ریاضی هشتم ➡️⬅️ – جهتدار و کامل!
- بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
- شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
- مثلث های هم نهشت 🌷🔺 گل سرسبد شکلهای هم‌نهشت!
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
- همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد میگیرید
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!
برای نصف کردن دایره نیازی نیست خط از مرکز دایره بگذرد این جمله درست است یا نادرست ؟
سلام و عرض ادب
غلط چون قطر دایره آن را نصف می کند که از نرکز آن می گذرد.
موفق باشید.
سلام
خطی که از مرکز دایره عبور کند و دو نقطه از محیط دایره را به هم متصل کند قطر دایره است و تنها همین پاره خط دایره را قطع می کند.
آیا دایره هم یک پاره خط است
سلام و عرض ادب
خیر، دایره یک منحنی بسته است و پاره خط قسمتی از یک خط است که دو سر آن بسته است.
موفق باشید.
سلام.ببخشید روش رسم مماس مشترک خارجی برای دو دایره چیه؟
با سلام وعرض ادب
از محل تماس دو دایره یک خط عبور دهید
اگر فاصله خطی تا مرکز دایره مساوی قطر دایره باشد خط دایره را در چند نقطه قطع میکند
با سلام وعرض ادب
در این صورت اصلا خط دایره رو قطع نمیکند
سلام
واضح است که قطر از شعاع بزرگتر است و چون فاصله مرکز دایره تا خط بیشتر از شعاع دایره هست،خط هیچ نقطه مشترکی با دایره ندارد.
سلام وقتتون استاد، یه سوال داشتم از خدمتتون: فاصله خطی تا مرکز دایره نصف شعاع می باشد در این صورت خط و دایره چند نقطه مشترک دارند؟؟ باتشکر
با سلام ووقت به خیر
در این صورت خط دایره را در دو نقطه قطع میکند
سلام
وقتی فاصله نصف شعاع باشد،یعنی خط درون دایره می باشد،حال مهم نیست که در شکل،خط دایره را قطع کرده یا خیر،چون در هر صورت امتداد خط،دایره
را قطع می کند
سلام ببخشید استاد یه سوال داشتم :فاصله ی خطی تا مرکز دایره برابر 5 سانتی متر و شعاع دایره 2 سانتی متر می باشد خط و دایره نسبت به هم چه وضعیتی دارند؟
با سلام وعرض ادب
دوست عزیز اگه دقت کنید جواب خیلی واضحه که خط نمیتونه دایره رو قطع کنه و خارج دایره هست
سلام استاد پس بقیه ویدیو هاتون کو؟؟؟☹️
با سلام واحترام
بقیه اش رو تهیه کنید واستفاده کنید
ممنون از توضیحات کامل شما
با سلاموعرض ادب
خواهش میکنم خوشحالیم که مفید بوده
با سلام و عرض احترام
خواهش میکنم و ممنون از توجه شما
سلام
فاصله مرکز دایره تا خطی برابر قطر همان دایره است خط و دایره چه وضعیتی با هم دارند؟
به چه صورت شکل را باید رسم کرد؟
با سلام وعرض ادب
خط خارج از دایره هست وآن را قطع نمیکند
سلام
چگونه می توان با یک خط کش مرکز دایره را مشخص کرد؟
با سلام وعرض ادب
اگه قطر رو دارید وسط قطر میشه مرکز
سلام این کلا اشتباهه
با سلام واحترام
دوست عزیز میشه دقیقا بگید کجاش اشتباهه تا ما تصحیح کنیم ؟
درحالتی که خط بر دایره مماس است چند نقطه مشترک دارند؟
سلام یک سوال داشتم در حالتی که خط بر دایره مماس است چند نقطه مشترک دارند؟
با سلام
یک نقطه
اگر فاصله مرکز دایره تا یک خط برابر شعاع دایره باشد خط بر دایره ……. است
جواب جاخالی چیه ؟؟
با سلام وعرض ادب
بر دایره مماس هست
سلام
کوتاه ترین وتر که از یک نقطه درون دایره میکذرد چطور؟
با سلام وادب
بلندترین وتر قطر هست ولی کوتاهترین وتر مشخص نیست چون هر اندازه ای در نظر بگیرید اندازه ای کوچکند از آن می‌شود تصور کرد
سلام میشه لطفا جواب بدین رابطه ی خط و دایره چیه؟
با سلام وادب
یه خط یا یه دایره رو قطع نمیکنه ونقطه مشترک ندارن یا مماس میشن ویه نقطه مشترک دارن یا خط دایره رو در دو نقطه قطع میکنه