قانون احتمال کل 🔣✅ – هرآنچه که نیاز دارید بدانید ?

در این درسنامه به توضیح قانون احتمال کل خواهیم‌پرداخت. پیش از بیان این قانون، لازم است تا با مفهوم افراز آشنا شویم.

افراز

فرض کنید \(\Large U \) یک مجموعه است و \(\Large A_1, A_2, \dots, A_n \) زیر‌مجموعه‌های \(\Large U \) هستند به طوری که:

\(\LARGE 1) A_i \neq \emptyset,\)  \(1 \leq i \leq n \)

\(\LARGE 2) A_1 \cup A_2 \cup \dots A_n=U\)

\(\LARGE 3) A_i \cap A_j=\emptyset,\)  \(i \neq j, 1 \leq i,j \leq n \)

در این صورت می‌گوییم \(\Large A_1, A_2, \dots, A_n \) مجموعه‌ی \(\Large U \) را افراز کرده‌اند. شکل زیر، شهود خوبی از مفهوم افراز به ما می‌دهد. همان طور که می‌بینید، در این شکل، مجموعه به وسیله‌ی زیر‌مجموعه‌های \(\Large A_1\) تا \(\Large A_6\) افراز شده‌است.

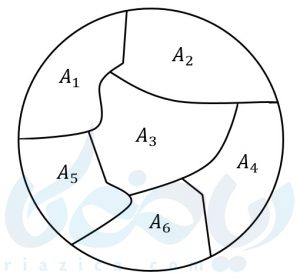
چند مثال برای درک افراز

در پست آموزش احتمال دهم، با مفهوم فضای نمونه و پیشامد آشنا شدید. می‌خواهیم با مفهوم افراز در فضای نمونه، با ذکر چند مثال آشنا شویم تا در انتها بتوانیم قانون احتمال کل را توضیح دهیم.

افراز در انداختن تاس

مثال 1: تاسی را پرتاب می‌کنیم. فضای نمونه برابر است با:

\(\LARGE S=\{1,2,3,4,5,6\}\)

پیشامد‌های زیر را در نظر بگیرید:

\(\LARGE A=\{1,3,5\}\)

\(\LARGE B=\{2,4,6\}\)

در این حالت، پیشامد‌های \(\Large A\) و \(\Large B\)، فضای نمونه را افراز کرده‌اند. زیرا سه شرطی که برای افراز گفتیم، برقرار است. یعنی داریم:

\( \LARGE 1)  A \neq \emptyset,\)  \(\Large B \neq \emptyset\)

\( \LARGE 2) A \cup B=S\)

\( \LARGE 3) A \cap B= \emptyset\)

مثال 2: در این قسمت به مثالی می‌پردازیم که در مسائل مربوط با قانون احتمال کل زیاد با آن سر‌و‌کار داریم. سه ظرف \(\Large A\) و \(\Large B\) و \(\Large C\) داریم که در هر کدام تعدادی مهره وجود دارد. چشم خود را می‌بندیم و از یکی از ظرف ها به تصادف، یک مهره بیرون می‌آوریم. می‌خواهیم پیشامد‌های ممکن در مورد انتخاب ظرف را بررسی کنیم. فضای نمونه برابر است با:

\(\LARGE S=\{A, B, C\}\)

پیشامد‌های \(\Large A\) و \(\Large B\) و \(\Large C\)، فضای نمونه را افراز کرده‌اند. زیرا اولا هیچ یک از پیشامد‌ها تهی نیستند. ثانیا، اجتماع پیشامد‌ها فضای نمونه را تشکیل می‌دهد. ثالثا، اشتراک آن‌ها تهی است. یعنی دستمان را همزمان در دو ظرف فرو نمی‌کنیم.

افراز در پرتاب سکه

مثال 3: حل این مثال نیز در فهم قانون احتمال کل، کمک زیادی به ما خواهد‌کرد. سکه‌ای را پرتاب می‌کنیم. پیشامد رو آمدن را با \(\Large F\) و پیشامد پشت آمدن را با \(\Large B\) نشان می‌دهیم. فضای نمونه برابر است با \(\Large S=\{F, B\}\). سه شرط افراز را بررسی می‌کنیم:

\( \LARGE 1)  F \neq \emptyset,\)  \(\LARGE B \neq \emptyset\)

\( \LARGE 2) F \cup B=S\)

\( \LARGE 3) F \cap B= \emptyset\)

پس در این حالت نیز، پیشامد‌های \(\Large F\) و \(\Large B\)، فضای نمونه را افراز می‌کنند.

اما اجازه دهید یک مثال هم از حالتی ببینیم که شرایط افراز برقرار نیست. درک درست افراز کمک شایانی به درک قانون احتمال کل خواهد‌کرد.

مثال 4: تاسی را پرتاب می‌کنیم. این بار پیشامد‌های زیر را در نظر بگیرید:

\( \LARGE A=\{1,2,3\}\)

\( \LARGE B=\{2,4\}\)

\( \LARGE C=\{5,6\}\)

هیچ یک از پیشامد‌ها تهی نیستند. از طرفی اجتماع آن‌ها، فضای نمونه را تشکیل می‌دهد. اما اشتراک دو پیشامد \(\Large A\) و \(\Large B\)، تهی نیست. یعنی داریم:

\( \LARGE A \cap B = \{2\}\)

پس پیشامد‌های \(\Large A\) و \(\Large B\) و \(\Large C\) فضای نمونه را افراز نمی‌کنند. حال که درک خوبی از مفهوم افراز داریم، می‌توانیم قانون احتمال کل را توضیح دهیم.

قانون احتمال کل

صورت قضیه:

فرض کنید \(\Large A_1, A_2, \dots, A_n \) پیشامد‌هایی باشند که فضای نمونه‌ی \(\Large S \) را افراز کنند و \(\Large B\) یک پیشامد دلخواه باشد. در این صورت، طبق قانون احتمال کل داریم:

\( \LARGE P(B)=P(A_1)P(B|A_1)\)

\( \LARGE +\dots+P(A_n)P(B|A_n)\)

\( \LARGE = \sum_{i=1}^{n}P(A_i)P(B|A_i)\)

همان طور که می بینید، علامت \(\Large \sum \) (بخوانید سیگما)در قانون احتمال کل، به معنی جمع چند جمله است. به همین خاطر از دیدن علامت \(\Large \sum \) نترسید.  همچنین \(\Large P(B|A_i) \) احتمال پیشامد \(\Large B\) به شرط \(\Large A_i\) است.

چند مثال برای درک قانون احتمال کل

شاید در نگاه اول، قانون احتمال کل کمی نا‌مفهوم به نظر برسد. با حل مثال‌های زیر، متوجه می شوید که استفاده از این قانون در حل مسائل مختلف، بسیار ساده است. همچنین با نمودار درختی در حل این مسائل آشنا می‌شویم که کارمان را بیش از پیش ساده می‌کند.

قانون احتمال کل در انتخاب مهره

مثال 5: دو ظرف داریم. در ظرف اول، 2 مهره‌ی آبی و 8 مهره‌ی قرمز داریم. در ظرف دوم، 4 مهره‌ی قرمز و 2 مهره‌ی آبی. چشممان را می‌بندیم و دست خود را به تصادف درون یکی از ظرف ها کرده و یک مهره بیرون می‌آوریم. احتمال اینکه مهره‌ی آبی بیرون بیاید چه‌قدر است؟

حل: برای حل مساله باید به دنبال پیشامد‌هایی باشیم که فضای نمونه را افراز کنند. همان طور که در مثال 2 دیدیم، پیشامد انتخاب ظرف‌ها فضای نمونه را افراز می‌کند. پیشامد انتخاب از ظرف اول را \(\Large A_1 \) و پیشامد انتخاب از ظرف دوم را \(\Large A_2 \) می‌نامیم. پیشامد خارج شدن مهره ی آبی را نیز با \(\Large B \) نمایش می‌دهیم. طبق قانون احتمال کل داریم:

\( \LARGE P(B)\)

\( \LARGE =\sum_{i=1}^{2}P(A_i)P(B|A_i)\)

\( \LARGE =P(A_1)P(B|A_1)\)

\( \LARGE +P(A_2)P(B|A_2)\)

پس باید رابطه‌ی بالا را محاسبه کنیم. احتمال انتخاب هر ظرف برابر با \(\Large \frac{1}{2} \) است. پس:

\( \LARGE P(A_1)=P(A_2)=\frac{1}{2}\)

پس تنها کافی است تا مقادیر \( \Large P(B|A_1)\) و \( \Large P(B|A_2)\) را به دست آوریم. \( \Large P(B|A_1)\) یعنی احتمال اینکه مهره‌ی آبی بیرون بیاید به شرط اینکه ظرف اول انتخاب شده باشد.

اگر ظرف اول انتخاب شده باشد، 2 مهره‌ی آبی و 8 مهره‌ی قرمز داریم. پس:

\( \LARGE P(B|A_1)=\frac{2}{8+2}=\frac{2}{10}\)

\( \Large P(B|A_2)\) یعنی احتمال اینکه مهره‌ی آبی بیرون بیاید به شرط اینکه ظرف دوم انتخاب شده باشد.

اگر ظرف دوم انتخاب شده باشد، 2 مهره‌ی آبی و 4 مهره‌ی قرمز داریم. پس:

\( \LARGE P(B|A_2)=\frac{2}{4+2}=\frac{2}{6}\)

حال می‌توانیم طبق قانون احتمال کل، مقدار\( \Large P(B)\) را به دست آوریم:

\( \LARGE P(B)=P(A_1)P(B|A_1)\)

\( \LARGE +P(A_2)P(B|A_2) \)

\( \LARGE  =\frac{1}{2} \times \frac{2}{10}+\frac{1}{2} \times \frac{2}{6}\)

\( \LARGE =\frac{4}{15}\)

حل مسائل قانون احتمال کل با نمودار درختی

مثال 6: سکه ای را پرتاب می‌کنیم. اگر رو بیاید، 2 بار دیگر و اگر پشت بیاید، 3 بار دیگر پرتاب می‌کنیم. احتمال اینکه دقیقا یکبار پشت بیاید چه قدر است؟

حل: پیشامد دقیقا یک بار پشت ظاهر شدن را با \( \Large R\) نمایش می‌دهیم. همچنین پیشامد رو ظاهر شدن در مرتبه ی اول را با \( \Large F_1\) و پشت ظاهر شدن در مرتبه ی اول را با \( \Large B_1\) نشان می‌دهیم. داریم:

\( \LARGE P(F_1)=P(B_1)=\frac{1}{2}\)

این دو پیشامد، فضای نمونه را افراز می‌کنند. اگر بار اول پشت بیاید، هر سه مرتبه ی بعدی باید رو بیاید. احتمال این پیشامد برابر است با:

\( \LARGE P(R|B_1)\)

\( \LARGE =\frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}=\frac{1}{8}\)

اگر بار اول رو بیاید، دقیقا یکی از دو مرتبه ی بعدی باید پشت بیاید. یعنی یا مرتبه ی دوم پشت، مرتبه ی سوم رو و یا بر عکس. احتمال این پیشامد برابر است با:

\( \LARGE P(R|F_1)=\frac{2}{4}\)

حال می‌توانیم طبق قانون احتمال کل، احتمال پیشامد \( \Large R\) را محاسبه کنیم:

\( \LARGE P(R)=P(B_1)P(R|B_1)\)

\( \LARGE +P(F_1)P(R|F_1)\)

\( \LARGE  =\frac{1}{2}\times\frac{1}{8}+\frac{1}{2}\times\frac{2}{4}\)

\( \LARGE =\frac{5}{16}\)

این مساله را می توانیم با رسم نمودار درختی نیز حل کنیم. به چه صورت؟ خیلی ساده. پیشامد‌های ممکن در هر مرحله‌ از مساله را در نظر می‌گیریم و احتمال هر پیشامد را روی شاخه می نویسیم. در انتها احتمال شاخه‌های مطلوب را در یکدیگر ضرب می کنیم. مانند شکل زیر:

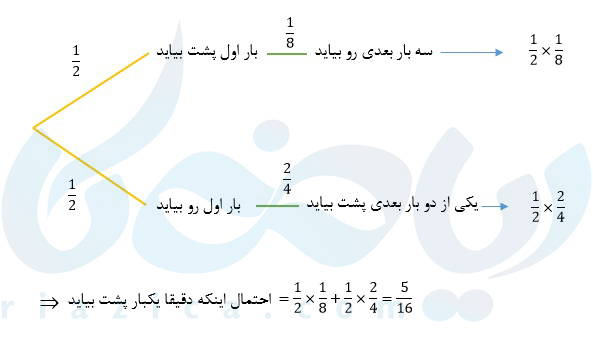
قانون احتمال کل در موفقیت و شکست

مثال 7: احتمال موفقیت فردی در آزمون اول \( \Large \frac{6}{10}\) و در آزمون دوم \( \Large \frac{4}{10}\)است. اگر این فرد در آزمون اول شکست بخورد، احتمال موفقیت در آزمون دوم \( \Large \frac{3}{10}\) است. احتمال اینکه حداقل در یکی از دو آزمون موفق شود چه قدر است؟

حل: با استفاده از قانون احتمال کل، مساله را حل خواهیم‌کرد. پیشامد موفقیت در یکی از دو آزمون را با \( \Large L\) نمایش می‌دهیم. همچنین پیشامد موفقیت در آزمون اول را با \( \Large A_1\) و پیشامد شکست در آزمون اول را با \( \Large F_1\) نشان ‌می‌دهیم. داریم:

\( \LARGE P(A_1)=\frac{6}{10},\) \( \Large P(F_1)=\frac{4}{10}\)

پیشامد موفقیت یا شکست در آزمون اول، فضای نمونه را افراز می‌کند. اگر در آزمون اول موفق شود، دیگر مهم نیست در آزمون دوم چه اتفاقی می‌افتد، چون شرط حداقلی مساله برآورده شده‌است. پس:

\( \LARGE P(L|A_1)=1\)

اما اگر در آزمون اول شکست بخورد، باید در آزمون دوم موفق شود. احتمال موفقیت در یکی از آزمون ها به شرط شکست در آزمون اول برابر است با:

\( \LARGE P(L|F_1)=\frac{3}{10}\)

حال می‌توانیم طبق قانون احتمال کل، احتمال پیشامد \( \Large L\) را محاسبه کنیم:

\( \LARGE P(L)=P(A_1)P(L|A_1) \)

\( \LARGE +P(F_1)P(L|F_1)  \)

\( \LARGE  =\frac{6}{10}\times 1+\frac{4}{10}\times\frac{3}{10} \)

\( \LARGE  =\frac{72}{100} \)

در تمام مسائل مربوط به قانون احتمال کل می‌توانید به عنوان راه حل جایگزین از نمودار درختی استفاده کنید. با در نظر گرفتن حالات مطلوب در این مساله و محاسبه‌ی احتمال هر شاخه، نمودار درختی این مساله به شکل زیر در می‌آید:

توصیه میشه قبل از خوندن این پست ،پست آموزش احتمال دهم رو مطالعه کنید.

زنگ آخر کلاس قانون احتمال کل

در این نوشتار مهم از مجموعهٔ آموزش ریاضی دوازدهم تجربی، ابتدا مفهوم افراز را معرفی کرده و سپس قانون احتمال کل را با هم مطالعه کردیم. با مثال‌های متنوعی که از مفهوم افراز و قانون احتمال کل حل کردیم، موضوع برایمان جا افتاد. حالا به سادگی می‌توانیم مسائل دیگر در این زمینه را حل کنیم. مطالب دیگری از آموزش ریاضی دوازدهم را نیز می‌تونید در وب‌سایت ریاضیکا مطالعه کنید.

هرچی سوال از این نوشتار آموزشی داشتید، زیر همین قسمت در بخش دیدگاه‌ها برای ما بنویسید. کارشناسان ریاضیکا به سوال‌های شما پاسخ می‌دهند.