آموزش ریاضی پایه هشتم
مثلث های هم نهشت 🌷🔺 گل سرسبد شکل‌های همنهشت!
تیر
یعنی مثلث ها رو هم مثل شکل های هم نهشت بچرخونم تا ببینم هم نهشت هستن یا نه؟ خب نه! مثلث های هم نهشت پارتی‌شون قویه… در این درس مهم از مجموعه آموزش ریاضی پایه هشتم ، ابتدا به بررسی مثلث های هم نهشت که حالتی خاص از شکل های هم نهشت هستند می‌پردازیم و حالت‌های هم نهشتی مثلث ها را معرفی می‌کنیم. همچنین حالت‌های دیگری برای مثلث‌های قائم‌الزاویه آموزش داده می‌شود تا ساده‌تر از این موضوع جذاب استفاده کنید.
مثلث های هم نهشت
همانطور که در درسنامه شکل های هم نهشت ریاضی هفتم خواندید مثلث های هم نهشت نوع خاصی از شکل های هم نهشت هستند که کاربرد زیادی در هندسه دارند. به همین دلیل در مثلث های هم نهشت ریاضی هشتم، حالت‌های هم نهشتی مثلث ها را یاد می‌گیریم. این موضوع در ریاضیات پایه‌های بالاتر مانند بحث تشابه مثلثها کاربرد دارد.
حالت‌های هم نهشتی مثلث ها – شاه‌کلید درس مثلث های هم نهشت
سه مثلث دلخواه در سه حالت مختلف با یکدیگر همنهشت هستند:
- برابری سه ضلع (ض ض ض): یعنی سه ضلع از یک مثلث با سه ضلع از مثلث دیگر برابر باشد؛
- برابری دو ضلع و زاویه بین (ض ز ض): یعنی دو ضلع و زاویه بین آنها با دو ضلع و زاویه بین مثلث دیگر برابر باشد؛
- برابری دو زاویه و ضلع بین (ز ض ز): یعنی دو زاویه و ضلع بین آنها با دو زاویه و ضلع بین مثلث دیگر برابر باشد.
این سه حالت را در شکل زیر به صورت خلاصه مشاهده می‌کنید:
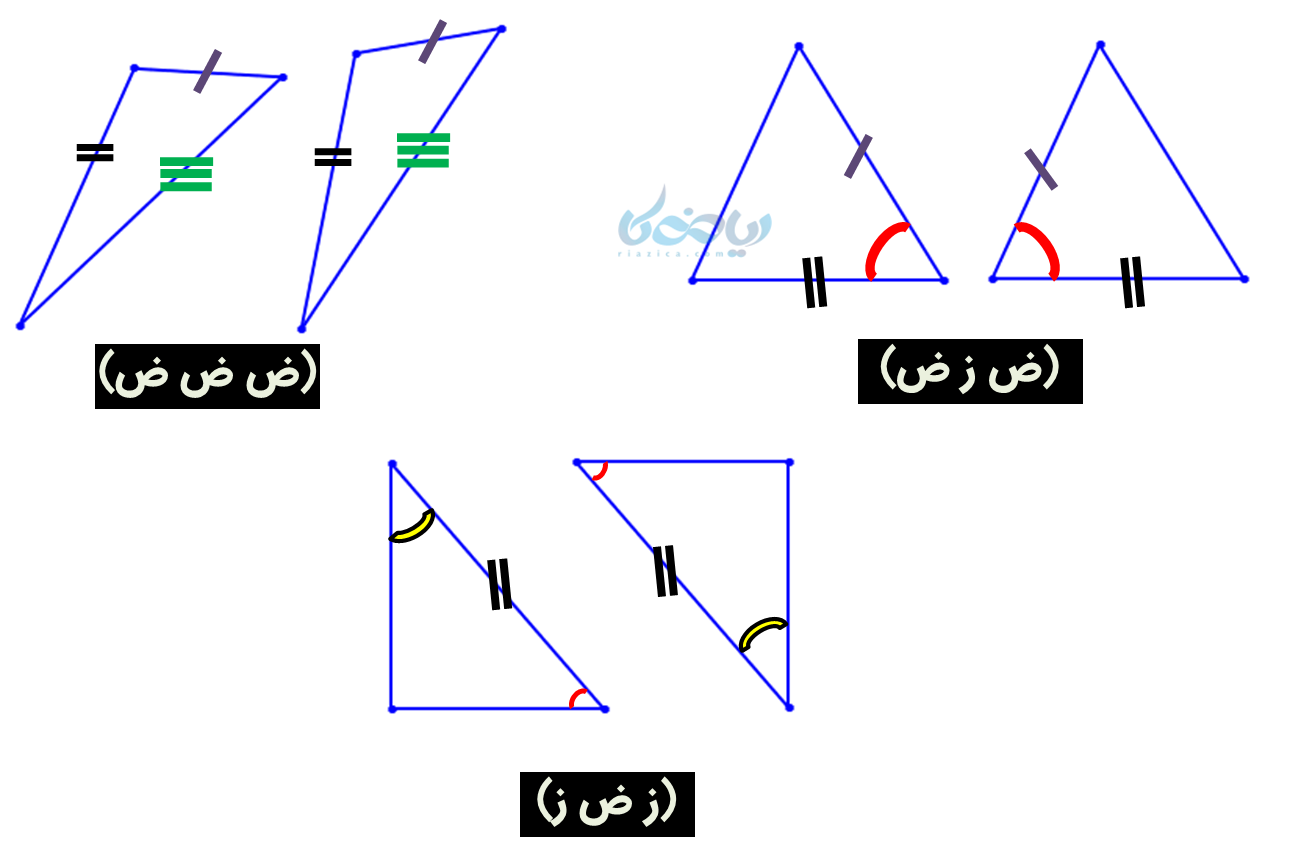
تذکر: برابری سه زاویه از دو مثلث (ز ز ز) لزوماً به معنای هم نهشتی مثلث ها نیست. مانند دو مثلث زیر:
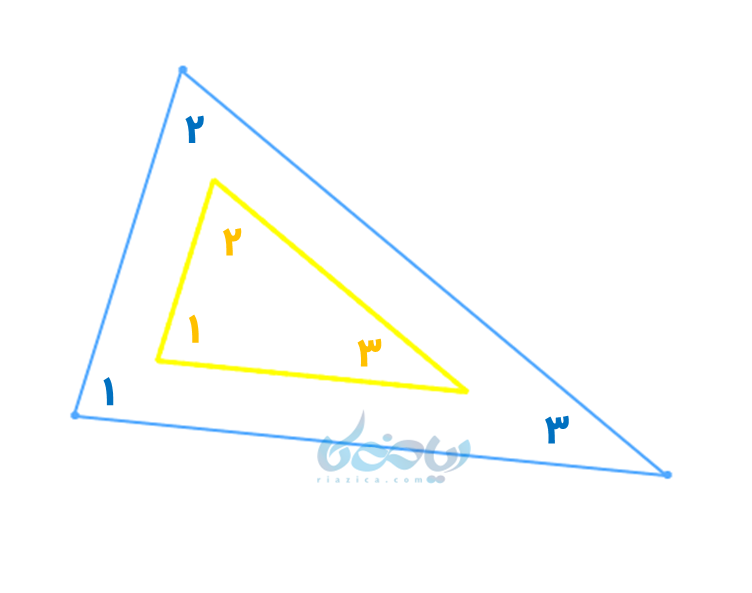
با این که زاویه‌های نشان داده شده (با نام‌های 1، 2 و 3) در دو مثلث برابرند، اما این دو، مثلث های هم نهشت نیستند.
مثال 1: حالت هم نهشتی مثلث ها را در شکل زیر تعیین کنید.
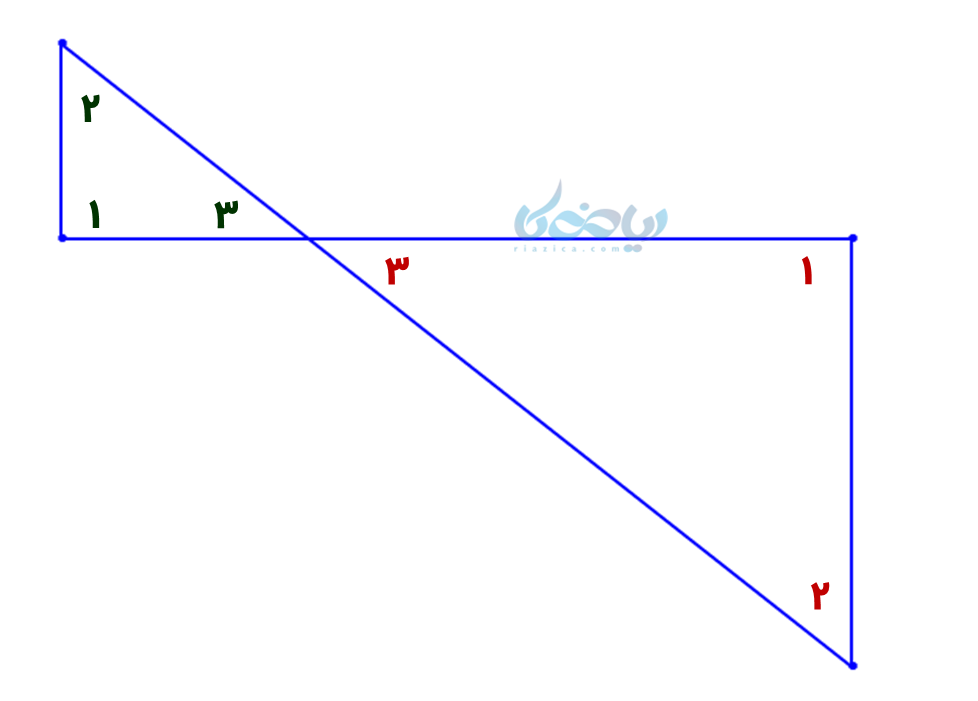
حل 1:
مشاهده می‌شود که سه زاویه از این دو مثلث با هم برابرند (ز ز ز) هم نهشت هستند؟؟؟ خیر!!! همنهشت نیستند. یادمان باشد … تعریف هم نهشتی این بود که با تبدیل‌های هندسی، دو شکل یکدیگر را کاملاً بپوشانند. این دو مثلث ضلع برابری ندارند. در درسنامه شکل های متشابه ریاضی نهم می بینید این دو مثلث متشابهند .
نکته (یادآوری از شکل‌های همنهشت): در مثلث های هم نهشت زاویه‌ها و ضلع‌های متناظر برابرند.
نکته: دقت کنید در حل مسائلی که از همنهشتی مثلثها استفاده می شود باید برای تساوی اضلاع وزاویه ها دلیل محکم طبق داده های مسئله داشته باشیم واز روی حدس وگمان وبدون دلیل نمی توان از حالت های هم نهشتی مثلث ها استفاده کرد.
مثال‌هایی ازکاربرد اثبات مثلث های هم نهشت
مثال 2: در هر یک از موارد زیر، حالت و دلیل هم نهشتی مثلث ها را بیان کنید.
الف) دو مثلث که از رسم یک قطر لوزی ایجاد شده است؛
ب) دو مثلث که از رسم یک قطر متوازی‌الاضلاع ایجاد شده است.
حل 2:
الف) یک لوزی مانند شکل زیر در نظر گرفته و یکی از قطرهای آن را (\( \Large \overline {AD} \)) رسم کرده‌ایم:
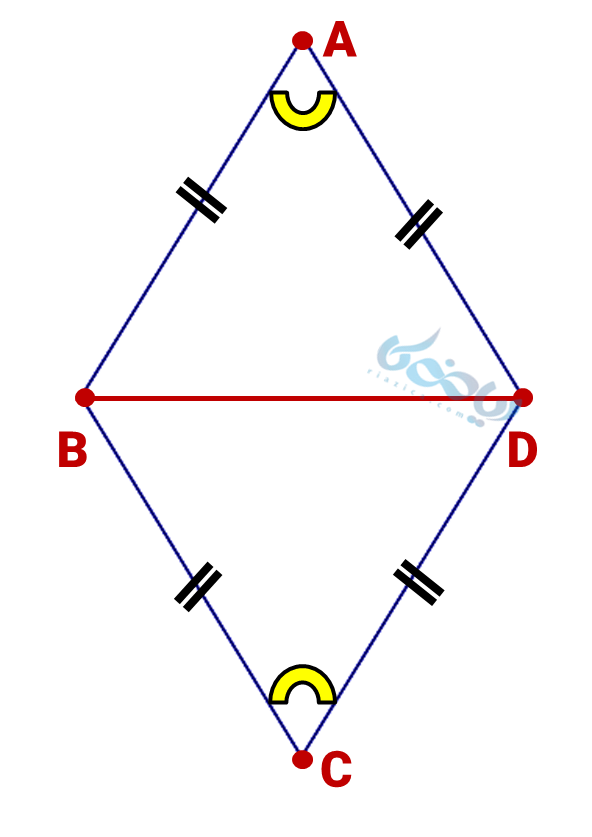
با توجه به ویژگی‌های لوزی که که در آن چهار ضلع برابر بوده و همچنین زاویه‌های روبرو با هم برابرند، دو مثلث \( \Large ABD \) و \( \Large CBD \) به حالت دو ضلع و زاویه بین (ض ز ض) همنهشت خواهند بود. به زیان ریاضی:
(برابری دو زاویه روبرو در لوزی) \( \Large \hat A = \hat C \)
(برابری اضلاع لوزی) \( \Large \overline{AB} = \overline{BC} \)
(برابری اضلاع لوزی) \( \Large \overline{AD} = \overline{CD} \)
\( \Large → \mathop {{\rm{ABD}}}\limits^\Delta \cong \mathop {{\rm{CBD}}}\limits^\Delta \)
ب) یک متوازی‌الاضلاع مانند شکل زیر در نظر گرفته و یکی از قطرهای آن را (\( \Large \overline {BD} \)) رسم کرده‌ایم:
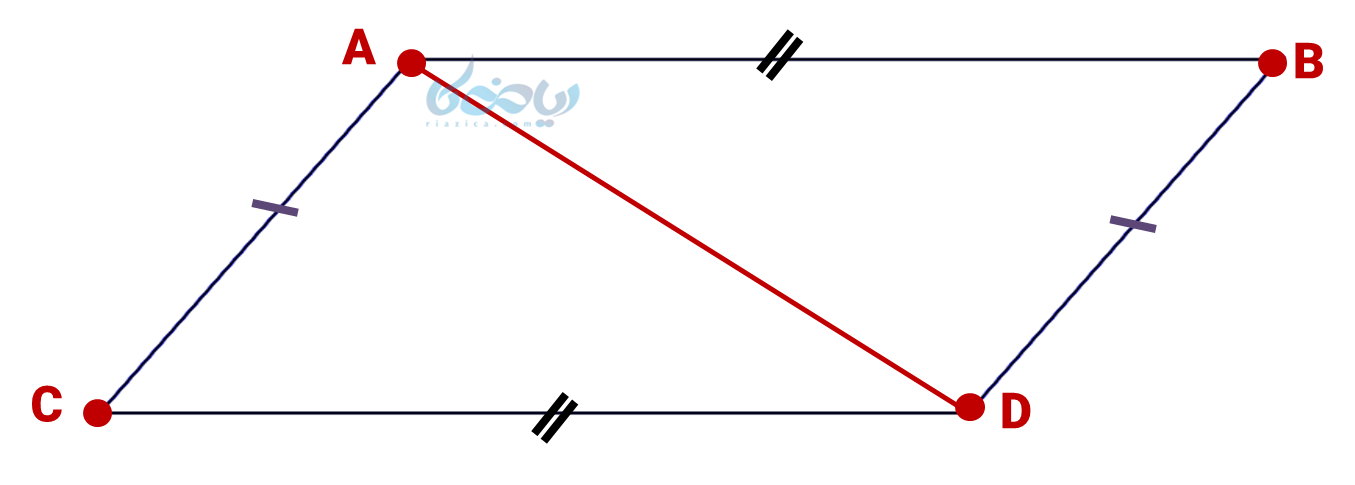
با توجه به ویژگی‌های متوازی‌الاضلاع که در آن اضلاع روبرو دو به دو برابرند، دو مثلث \( \Large ABD \) و \( \Large ACD \) به حالت برابری سه ضلع (ض ض ض) هم نهشت خواهند بود. به زیان ریاضی:
(برابری اضلاع روبرو متوازی‌الاضلاع)\( \Large \overline{AB} = \overline{CD} \)
(برابری اضلاع روبرو متوازی‌الاضلاع)\( \Large \overline{AC} = \overline{BD} \)
(ضلع مشترک دو مثلث)\( \Large \overline{AD} = \overline{AD} \)
\( \Large → \mathop {{\rm{ABD}}}\limits^\Delta \cong \mathop {{\rm{ACD}}}\limits^\Delta \)
مثال دایره‌ای این درس
مثال 3: در شکل زیر مشخص کنید که آیا این دو مثلث، مثلث های هم نهشت هستند؟ اگر جواب مثبت است، حالت هم نهشتی مثلث ها را مشخص کرده و سپس مجهولات مسأله را بدست آورید.
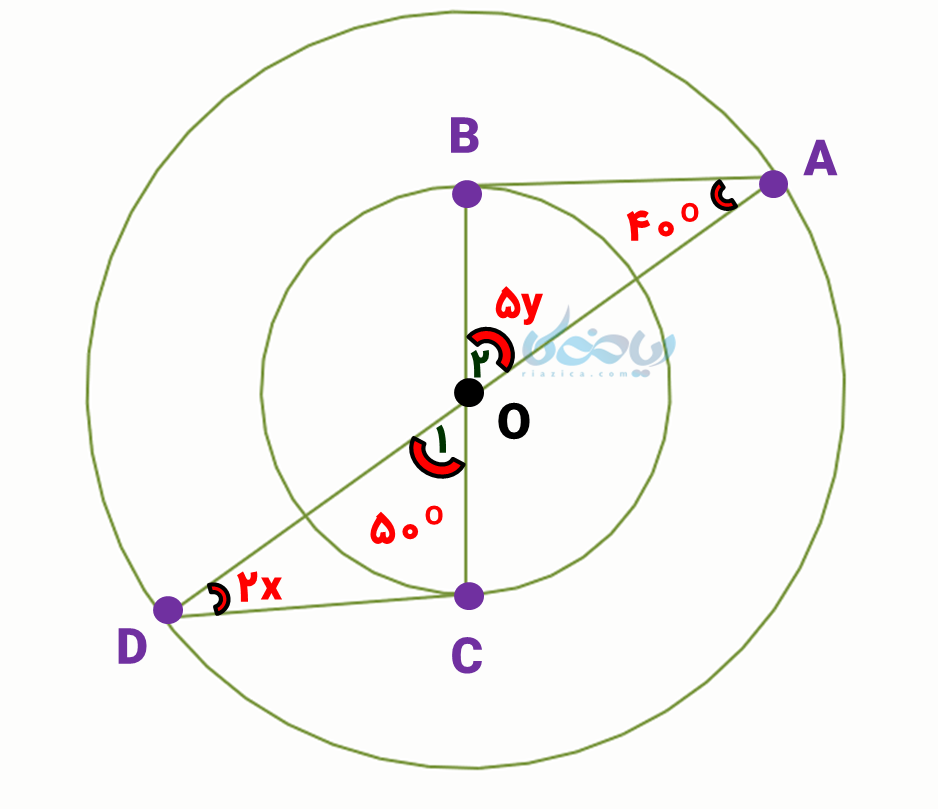
حل 3:
در این شکل دو دایره هم‌مرکز رسم شده‌اند و قطرهای دو دایره اضلاع دو مثلث \( \Large OAB \) و \( \Large OCD \) را تشکیل داده‌اند. برابری‌های زیر در این دو مثلث مشاهده می‌شود:
(شعاع‌های دایره کوچک) \( \Large \overline{OB} = \overline{OC} \)
(شعاع‌های دایره بزرگ) \( \Large \overline{OD} = \overline{OA} \)
(متقابل به راس)\( \Large \hat {O_1} = \hat {O_2} \)
\( \Large → \mathop {{\rm{OAB}}}\limits^\Delta \cong \mathop {{\rm{OCD}}}\limits^\Delta \)
بنابراین دو مثلث \( \Large OAB \) و \( \Large OCD \) به حالت برابری سه ضلع (ض ز ض) هم نهشت هستند.
با توجه به این نکته که در مثلث های هم نهشت اضلاع و زوایای متناظر برابرند، پس زاویه‌های روبرو به ضلع‌های برابر با هم برابرند؛ یعنی:
\( \Large \hat A = \hat D→ 40° = 2x \)
\( \Large → x = \frac {40}{2} = 20° \)
\( \Large \hat {O_1} = \hat {O_2}→ 50° = 5y \)
\( \Large → y = \frac {50}{5} = 10° \)
حالت‌های هم نهشتی مثلث های قائم‌الزاویه
علاوه بر 3 حالت قبلی (که برای هر نوع مثلثی کاربرد دارد)، دو مثلث قائم‌الزاویه، بنا به دو حالت با یکدیگر هم نهشت خواهند بود:
- برابری وتر و یک ضلع (و ض): یعنی وتر و یک ضلع از یک مثلث قائم‌الزاویه با وتر و یک ضلع از مثلث قائم‌الزاویه دیگر برابر باشد؛
- برابری وتر و یک زاویه تند (و ز): یعنی وتر و یک زاویه تند از یک مثلث قائم‌الزاویه با وتر و یک زاویه تند از مثلث قائم‌الزاویه دیگر برابر باشد.
حالت‌های هم نهشتی مثلث‌های قائم‌الزاویه را در شکل زیر به صورت خلاصه شده مشاهده می‌کنید:
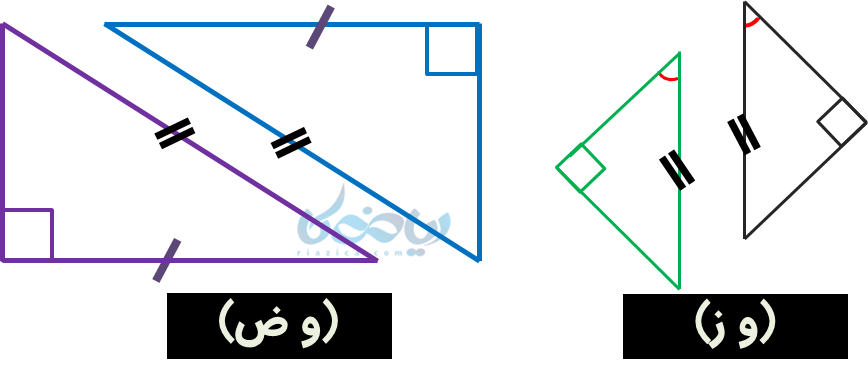
مثال 4: در دو مثلث زیر مقادیر \( \Large x \) و \( \Large y \) را بدست آورید.
حل 4:
طبق مفروضاتدر نظر گرفته شده در شکل در مثلث‌های \( \Large OAB \) و \( \Large OCD \) برابری‌های زیر برقرار است:
\( \Large \hat A = \hat C \)
\( \Large \overline {AB} = \overline {CD} \)
بنابراین با توجه به قائم‌الزاویه بودن، به حالت وتر و یک زاویه تند (و ز) هم نهشت هستند. از آنجا که اجزای متناظر در مثلث های هم نهشت با هم برابرند، خواهیم داشت:
\( \Large \hat D = \hat B→ x = 40° \)
\( \Large \overline {OB} = \overline {OD} → 5y = 20 \)
\( \Large → y = \frac {20}{5} = 4 \)
اثبات حالت هم نهشتی اول ( و ض)
در شکل زیر دو مثلث قائم‌الزاویه دیده می‌شود که وتر و یک ضلع آن دو برابرند. بیایید رابطه فیثاغورس را برای این دو مثلث بنویسیم:
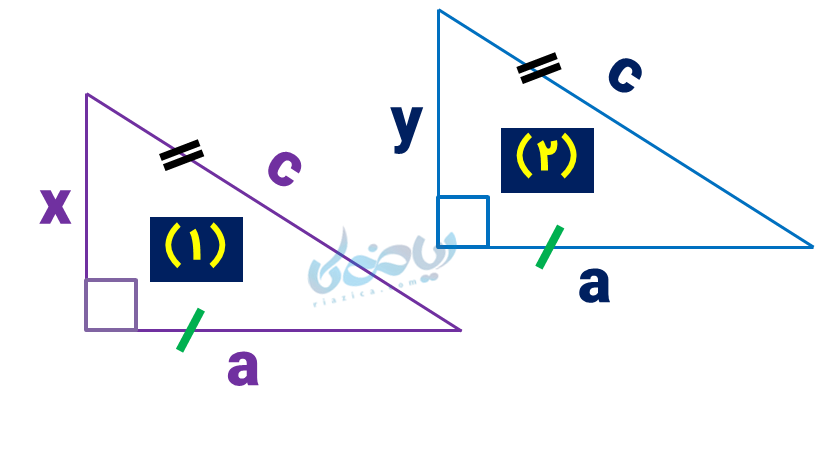
(مثلث 1) \( \Large x^2 + a^2 = c^2 \)
(مثلث 2) \( \Large y^2 + a^2 = c^2 \)
اگر این دو رابطه را مقایسه کنیم، خواهیم دید که \( \Large x = y \)؛ یعنی ضلع سوم دو مثلث هم برابر شده است. بنابراین مثلث‌های (1) و (2)، مثلث های هم نهشت از نوع (ض ض ض) خواهد بود.
اثبات حالت هم نهشتی دوم ( و ز)
در شکل زیر دو مثلث قائم‌الزاویه داریم که وتر و یک زاویه تند در آن دو برابرند (زاویه \( \Large \hat A \) در مثلث 1 و زاویه \( \Large \hat K \) در مثلث 2).
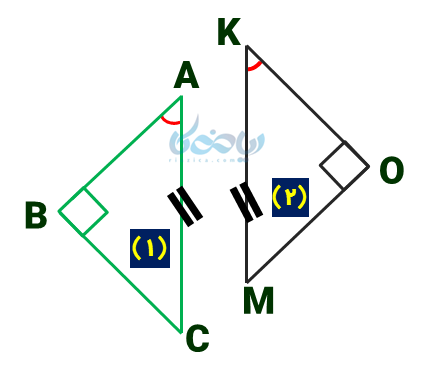
می‌دانیم که مجموع زاویه‌های داخلی مثلث برابر با °180 است (یادآوری: درس زاویه های داخلی). این رابطه را برای هر دو مثلث می‌نویسیم:
(مثلث 1) \( \Large \hat A + \hat B + \hat C = 180° \)
(مثلث 2) \( \Large \hat K + \hat O + \hat M = 180° \)
با توجه به این که زوایای \( \Large \hat B \) و \( \Large \hat O \) برابر با °90 بوده و زوایای زوایای \( \Large \hat A \) و \( \Large \hat K \) با هم برابرند، این دو رابطه را به این شکل می‌نویسیم:
(مثلث 1) \( \Large \hat A + 90° + \hat C = 180° \)
(مثلث 2) \( \Large \hat A + 90° + \hat M = 180° \)
اگر به این دو رابطه توجه کنیم، متوجه خواهیم شد که زوایای \( \Large \hat C \) و \( \Large \hat M \) برابرند، پس دو مثلث به حالت (ز ض ز) همنهشت هستند:
\( \Large \hat A = \hat K \)
\( \Large \overline {AC} = \overline {KM} \)
\( \Large \hat C = \hat M \)
میوه‌های درخت « مثلث های هم نهشت »
با استفاده از هم نهشتی مثلث ها، قضیه ها ومسئله های زیادی را می توان در هندسه اثبات کرد که ما در این درسنامه دو قضیه مهم واثبات آنها را برای شما آورده ایم.ابتدا به دو نکته مهم زیر توجه کنید:
یادآوری 1: فاصله دو نقطه از هم برابر طول پارهخطی است که آن نقاط را به هم وصل می کند.
یادآوری 2: فاصله یک نقطه از یک خط، برابر طول پارهخطی است که از آن نقطه بر آن خط عمود می شود.
قضیه اول
هر نقطه روی عمودمُنَصّف یک پاره خط از دو سر آن پاره‌خط به یک فاصله است.
اثبات قضیه اول:
پارهخطی مانند AB در نظر گرفته و عمودمنصف آن (یعنی OH) را رسم می‌کنیم. عمودمنصف، پاره‌خط را نصف کرده و بر آن عمود می‌شود.
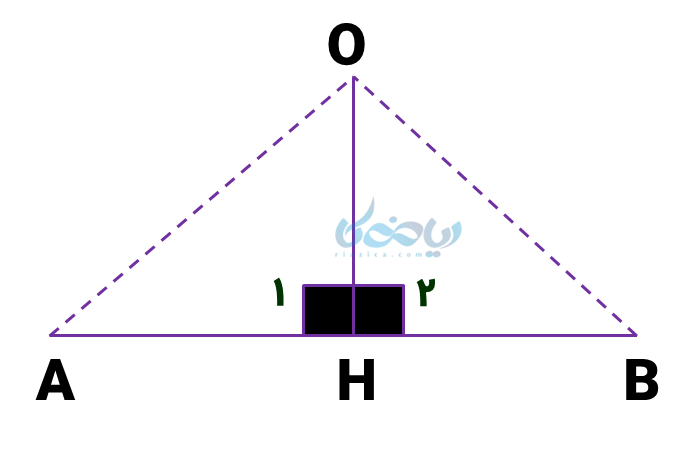
فاصله یک نقطه از عمودمنصف (مانند نقطه O) از دو سر پاره‌خط در این شکل، پاره‌خط‌های OA و OB هستند. در دو مثلث ایجاد شده، این برابری‌ها را می‌بینیم:
\( \Large \hat {H_1} = \hat {H_2} = 90° \)
(عمودمنصف) \( \Large \overline {AH} = \overline {HB} \)
(ضلع مشترک) \( \Large \overline {OH} = \overline {OH} \)
این روابط نشان می‌دهد که دو مثلث AOH و BOH به حالت (ض ز ض) مثلث های هم نهشت هستند. با توجه به تساوی اجزای متناظر: \( \Large \overline {OA} = \overline {OB} \)
عکس این قضیه نیز برقرار است یعنی هر نقطه که از دو سر یک پاره خط به یک اندازه باشد حتما روی عمود منصف آن پاره خط قرار دارد.
جالب است بدانید عکس این قضیه را هم می توان از راه هم نهشتی مثلث ها اثبات کرد.
قضیه دوم
هر نقطه روی نیمساز یک زاویه از دو ضلع زاویه به یک فاصله است.
اثبات قضیه دوم:
زاویه‌ای مانند \( \Large \hat O \) در نظر گرفته و نیمساز آن را رسم می‌کنیم (خط نقطه‌چین). فاصله نقطه‌ای مانند M بر روی نمیساز تا دو ضلع زاویه، طول پارهخطی است که از آن نقطه بر آن دو خط عمود می شود.
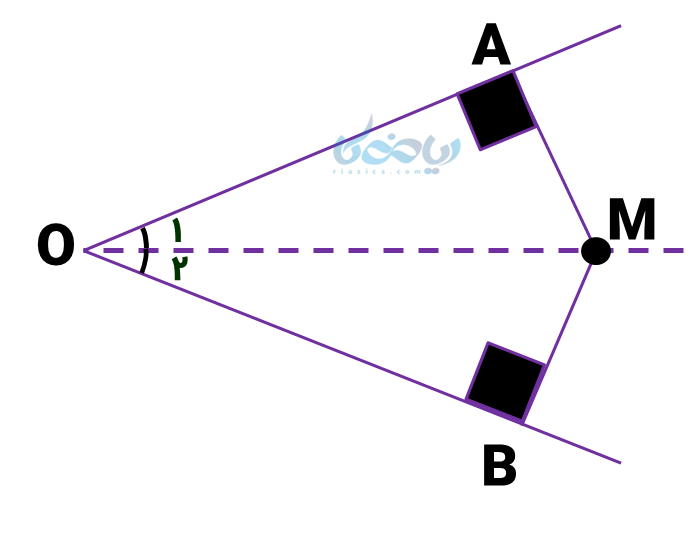
با رسم این دو پاره‌خط (یعنی AM و BM) دو مثلث قائم‌الزاویه ایجاد می‌شود که می‌توان برابری‌های زیر را برای آنها نوشت:
(نیمساز) \( \Large \hat {O_1} = \hat {O_2} = 90° \)
(ضلع مشترک) \( \Large \overline {OM} = \overline {OM} \)
این روابط نشان می‌دهد که دو مثلث قائم‌الزاویه AOM و BOM به حالت (و ز) مثلث های هم نهشت هستند. با توجه به تساوی اجزای متناظر: \( \Large \overline {AM} = \overline {BM} \)
نکته: عکس قضیه دوم هم برقرار است؛ یعنی نقطه‌ای که فاصله آن تا دو ضلع زاویه برابر است، روی نیمساز زاویه قرار دارد.
برای یادگیری بیشتر این مبحث می توانید به درسنامه هم نهشتی مثلث ها نهم مراجعه کنیدو
قسمتی از فایل ویدیویی مثلث های هم نهشت
برای خرید این دو ویدیو درباره مثلث های هم نهشت دکمه خرید زیر را بزنید:
زنگ آخر کلاس مثلث های هم نهشت
در این مطلب به یادگیری حالت خاص و مهمی از شکل‌های همنهشت یعنی مثلث های هم نهشت و حالت‌های هم نهشتی مثلث ها پرداختیم که در هندسه بسیار پرکاربرد هستند. برای مثلث‌های قائم‌الزاویه نیز حالت‌های دیگری معرفی کردیم و با استفاده از آن دو قضیه کاربردی در هندسه را یاد گرفتیم.مطمئناً با مثال‌های مختلفی که حل کردیم، از این به بعد می‌توانیم با قدرت با این‌گونه مسائل مواجه شویم.
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاه‌ها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.
ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی هشتم به شما پیشنهاد می‌دهیم:
- زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعیها!
- اعداد صحیح ↔️➖➕– نمایش روی محور مختصات
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعیها!
- تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
- عدد اول ریاضی هشتم 1️⃣👨🎓 – کاملترین آموزشی که لازم داشتید.
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- خط و دایره : از سیر ➖ تا پیاز 🔴
- خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خطها در چهارراه زاویه!
- چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!
- ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
- فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارتهای جبری استفاده کن!
- حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
- بردار و مختصات ریاضی هشتم ➡️⬅️ – جهتدار و کامل!
- بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
- شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
- مثلث های هم نهشت 🌷🔺 گل سرسبد شکل‌های همنهشت!
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
- همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد میگیرید
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!
سلام چرا سه زاویه برابر برای هم نهشتی استفاده نمی شود
سلام و عرض ادب
وقتی سه زاوبه برابر باشند متشابه هستند. نمی توان نتیجه گرفت که لزوما با هم برابرند.
موفق باشید.
سلا
چون هم نهشتی یعنی شکلی که هم ضلع های آن برابرباشد هم زاویه های آن اگر به مطالب بالا دقت میکردید متوجه می شدید که درشکی بزرگ و کوچک زاویه هاربر بود اگر باکاغذ پوستی یا طلق شکل ۱ را روی شکل۲ منطبق کنی برابر نیست .
پس رابطه ز ز ز نادرست می باشد.
علامت شکل های متشابه جدید چه جوریع
با سلام و ادب
علامتش ~ هست
تعداد مثلث های هم نهشت با یک مثلث؟
با سلام وعرض ادب
با یه مثلث ممکنه بی نهایت مثلث همنهشت باشن
سلام ممنون از شما
با سلام واحترام
خواهش می‌کنم دوست گرامی
سلام
میخواستم بدونم ممکنه دو مثلت به چند حالت همنهشت باشند واگر ممکنه ما اجازه داریم چندحالت رو بنویسیم
ممنون میشم اگرپاسخ بدین
با سلام وعرض ادب
بله میشه به چند حالت برابر بشن ومیتونید همه حالتها رو بنویسید اما لازم نیست یک حالت رو بنوبیید کافیه
سلام آیا در هر مثلث که مساحت های برابر داشته باشند هم نهشت هستند ؟
با سلام وادب
خیر مثلثها میتوانند دارای مساحتهای برابر باشند وهمنهشت نباشند
سلام چه جوری ثابت میشه که اگر وسط اضلاع یک مثلث را به هم وصل کنیم ۴ مثلث کوچک ایجاد شده همنهشت هستند و ۴ تا شون با مثلث بزرگ متشابه اند ؟
سلام خسته نباشید ممنون از مطالب خوبتون فقط یه سوال چطور مطمئن بشیم که حالت های هم نهشتی رو درست نوشتیم؟
با سلام وادب
اگه به اون ضلعها وزاویه هایی که تساویشون رو با دلیل منطقی نوشتید دقت کنید وبا سه حالت مقایسه کنید خودتون متوجهمیشید
عع یک عدد کیپاپر در سایت ریاضی پیدا شد?من خودم آرمی،بلینک،استی،موآ،وانس،اکسوال،و …ام
ممنونه از تون مطالب های خوب ومفید داشت بازم ممنونه از کمکتون که این سایت روزدیدمرسی❤
یا سلام ودرود
با معرفی سایت ما به دوستان ماررو یاری کنید
سلام میشه یه تعریف کلی و مختصر از قضیه‌ی فیثاغورس بکنید؟ ممنون
با سلام وادب
این قضیه میگه در مثلث قائم الزاویه مجذور وتر برابرست با مجموع مجذورت دوضلع دیگر
برای ثابت کردن اینکه مثلث قائم الزاویه است به کار میره
عالی، هایا
با سلام وادب
ممنون از انرژی شما
سلام ممنون از مطالب مفیدتون
سوالی داشتم ازخدمتتون که آیا اثبات مثلث ها قانون یا روش مشخصی داره؟
به طور مثال شما در مثال دایره ای هم نهشتی رو به حالت۳ض(ض ض ض)اثبات کردید.اما من به حالت(ض ز ض).{o1=o2},{oB=oC},{oD=oA}
پاسخ من هم میتونه درست باشه یا فقط یک پاسخ درست داریم اون هم به حالت۳ضلعی که شما اثبات کردید.
پیشاپیش ممنون از پاسخگوییتون??
سلام دوست عزیز
گاهی یک مسئله رو میشه از چند روش حل کرد مهم اینه که برای درستی تساویها دلیل داشته باشید