تعریف توان ریاضی هفتم ✳️📝 – مفهوم و کاربردش!

در درسنامهٔ تعریف توان ریاضی هفتم ابتدا توان را معرفی می‌کنیم. سپس، کاربرد توان در محاسبهٔ مساحت و تجزیهٔ اعداد را بررسی می‌کنیم. همان طور که خواهید دید، تجزیهٔ اعداد با استفاده از مفهوم توان به ما در یافتن ب.م.م و ک.م.م نیز کمک خواهد کرد. با ما تا انتهای درسنامه همراه باشید.

تعریف توان

وقتی می‌نویسیم \(\Large 2^3\) و می‌خوانیم “\(\Large 2\) به توان \(\Large 3\)” یعنی \(\Large 2\) را \(\Large 3\) بار در خودش ضرب کرده‌ایم. به عبارت دیگر، داریم:

\(\LARGE  2^3=2 \times 2 \times 2 \)

در عبارت \(\Large 2^3\) به \(\Large 2\)، پایه و به \(\Large 3\)  ،توان می‌گوییم.

ممکن است بپرسید نمایش با استفاده از اعداد توان دار چه کاربردی دارد؟ اولین کاربرد این نوع نمایش، خلاصه‌نویسی است. مثلاً اگر در یک مسئله مجبور بودیم عدد \(\Large 4 \) را \(\Large 5 \) بار در خودش ضرب کنیم، طبیعتا راحت‌تریم از عبارت \(\Large 4^5 \) استفاده کنیم. کاربرد نمایش با استفاده از اعداد توان دار به ساده سازی نوشتاری محدود نمی‌شود. یک کاربرد ابتدایی و مهم دیگر اعداد توان دار، در تجزیهٔ اعداد و پیدا کردن ب.م.م و ک.م.م است (در درسنامهٔ بزرگترین شمارنده مشترک با ب.م.م و در درسنامهٔ کوچکترین شمارندهٔ مشترک با ک.م.م آشنا شدیم). در انتهای درسنامهٔ تعریف توان ریاضی هفتم روش به دست آوردن ب.م.م و ک.م.م با کمک گرفتن از مفهوم توان را خواهیم دید.

مثال از محاسبهٔ توان

مثال 1: هر یک از مقادیر \(\Large (-2)^3 \) و \(\Large 1.2^2 \) و \(\Large (\frac{3}{5})^3 \) و \(\Large (-3)^2 \) را محاسبه کنید.

حل: کافی است از تعریف توان استفاده کنیم. برای محاسبهٔ \(\Large (-2)^3 \) باید \(\Large (-2) \) را \(\Large 3 \) بار در خودش ضرب کنیم:

\( (-2)^3=(-2) \times (-2) \times (-2) =-8 \)

برای محاسبهٔ \(\Large 1.2^2 \) باید \(\Large 1.2 \) را \(\Large 2 \) بار در خودش ضرب کنیم:

\(\LARGE 1.2^2=1.2 \times 1.2=1.44 \)

برای محاسبهٔ \(\Large (\frac{3}{5})^3 \) باید \(\Large \frac{3}{5} \) را \(\Large 3 \) بار در خودش ضرب کنیم:

\(\LARGE (\frac{3}{5})^3=\frac{3}{5} \times \frac{3}{5} \times \frac{3}{5}=\frac{27}{125} \)

برای محاسبهٔ \(\Large (-3)^2 \) باید \(\Large (-3) \) را \(\Large 2 \) بار در خودش ضرب کنیم:

\(\LARGE (-3)^2=(-3) \times (-3) =9 \)

مجذور و مکعب

اگر عددی را به توان \(\Large 2 \) برسانیم، اصطلاحاً مجذور آن را حساب کرده‌ایم. همچنین، اگر عددی را به توان \(\Large 3 \) برسانیم، اصطلاحاً مکعب آن را محاسبه کرده‌ایم. به طور مثال، مجذور عدد \(\Large 5 \) برابر است با:

\(\LARGE 5^2=5 \times 5=25 \)

یا مثلاً مکعب عدد \(\Large 4 \) برابر است با: 

\(\LARGE 4^3=4 \times 4 \times 4=64 \)

به قسمت بعدی از درسنامهٔ تعریف توان ریاضی هفتم توجه کنید.

نکات کلیدی توان هفتم

در محاسبهٔ اعداد توان‌دار، موارد زیر را نیز می‌توان با استفاده از تعریفی که کردیم نتیجه‌گیری کرد:

• عدد \(\Large 1 \) به توان هر عددی برابر با \(\Large 1 \) است. به عبارت دیگر، \(\Large 1^a=1 \)؛ زیرا \(\Large 1 \) را هر چند بار که در خودش ضرب کنیم، برابر با \(\Large 1 \) می‌شود.
• هر عددی به توان \(\Large 1 \) برابر با خودش است. به عبارت دیگر، \(\Large a^1=a \)؛ زیرا اگر یک عدد، در عدد دیگری ضرب نشود، برابر با خودش می‌شود.
• صفر به توان هر عددی به غیر از صفر، برابر با صفر است. به عبارت دیگر، \(\Large 0^a=0 \)؛ زیرا صفر را هر چند بار در خودش ضرب کنیم، باز هم حاصل صفر خواهد شد.
• هر عددی به توان صفر برابر با یک است. به عبارت دیگر، \(\Large a^0=1 \)؛ دلیل این امر را در درسنامهٔ ساده کردن عبارت های توان دار توضیح خواهیم داد.

برای علاقه‌مندان: اگر دقت کنید، در مواردی که بیان کردیم، در مورد صفر به توان صفر صحبتی نکردیم. در برخی از مباحث ریاضی، \(\Large 0^0 \) را برابر با \(\Large 1 \) و در برخی، \(\Large 0^0 \) را تعریف نشده در نظر می‌گیرند. اگر مایل بودید در مورد این مطلب مطالعه کنید.

در قسمت‌های بعدی از درسنامهٔ تعریف توان ریاضی هفتم به کاربرد توان در مباحث مختلف می‌پردازیم.

کاربرد توان در محاسبهٔ مساحت

مساحت مربعی به ضلع \(\Large a \) برابر است با \(\Large a \times a\). حال که توان را تعریف کرده‌ایم، می‌توانیم مساحت مربعی به ضلع \(\Large a \) را با \(\Large a^2 \) نمایش دهیم. همچنین، پیش از این مساحت دایره‌ای با شعاع \(\Large r \) را با عبارت \(\Large \pi \times r \times r \) نمایش می‌دادیم. اکنون می‌توانیم مساحت دایره‌ای با شعاع \(\Large r \) را با عبارت \(\Large \pi r^2 \) نشان دهیم. در شکل زیر، دو مطلبی که گفتیم نشان داده شده است.

کاربرد توان در تجزیهٔ اعداد

در درسنامهٔ شمارنده اول ریاضی هفتم با تجزیهٔ اعداد و یافتن شمارنده‌های اول آن‌ها آشنا شدیم. به طور مثال دیدیم که عدد \(\Large 12 \) به صورت زیر تجزیه می‌شود:

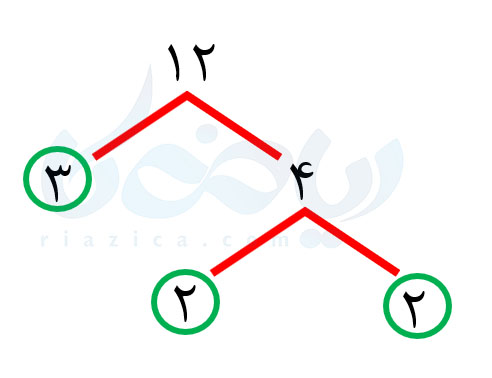
یعنی می‌توانیم عدد \(\Large 12 \) را به صورت حاصل ضرب شمارند‌ه‌های اول به شکل زیر بنویسیم:

\(\LARGE 12=2 \times 2 \times 3 \)

همان طور که می‌بینید، عدد \(\Large 2 \) دوبار در حاصل ضرب بالا آمده است. با استفاده از توان می‌توانیم عبارت بالا را به صورت زیر بازنویسی کنیم:

\(\LARGE 12=2 ^2 \times 3 \)

این نمایش به ما کمک می‌کند تا روش به دست آوردن ب.م.م و ک.م.م را با استفاده از تجزیهٔ اعداد، به زبان ساده‌تری بیان کنیم:

• ب.م.م دو یا چند عدد برابر است با حاصل ضرب پایه‌های مشترک با کوچکترین توان
• ک.م.م دو یا چند عدد برابر است با حاصل ضرب پایه‌های مشترک با بیشترین توان در پایه‌های غیر مشترک.

برای اینکه بهتر متوجه شوید، به مثال‌های بعدی از درسنامهٔ تعریف توان ریاضی هفتم دقت کنید.

مثال از درسنامهٔ تعریف توان ریاضی هفتم

مثال 2: ب.م.م و ک.م.م دو عدد \(\Large 72 \) و \(\Large 84 \) را بیابید.

حل: ابتدا دو عدد را با استفاده از آنچه که در درسنامهٔ شمارنده اول ریاضی هفتم خواندیم، تجزیه می‌کنیم. تجزیهٔ عدد \(\Large 72 \) به صورت زیر است:

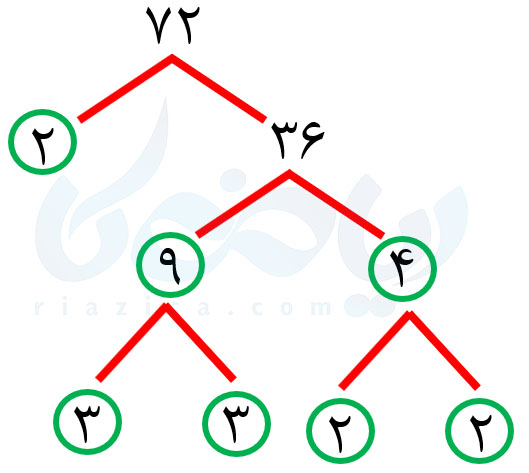
عدد \(\Large 84 \) نیز به صورت زیر تجزیه می‌شود:

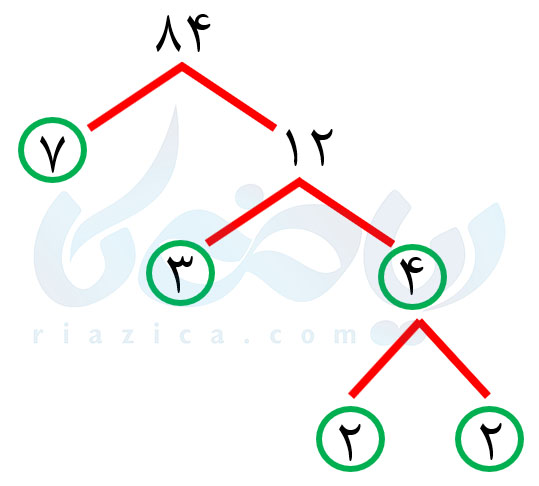
با استفاده از تجزیهٔ بالا و مفهوم توان، می‌توانیم دو عدد \(\Large 72 \) و \(\Large 84 \) را به صورت زیر بنویسیم:

\(\LARGE  72=2^3 \times 3^2 \)

\(\LARGE  84=2^2 \times 3 \times 7 \)

همان طور که گفتیم، برای به دست آوردن ب.م.م باید پایه‌های مشترک را با کوچکترین توان در هم ضرب کنیم. پایه‌های \(\Large 2 \) و \(\Large 3 \) بین دو عدد مشترک هستند. کوچکترین توان پایهٔ \(\Large 2 \) در عدد \(\Large 84\) وجود دارد و برابر با \(\Large 2\) است. کوچکترین توان پایهٔ \(\Large 3\) نیز در عدد \(\Large 84\) وجود دارد و برابر با \(\Large 1 \) است (در واقع چون پایهٔ \(\Large 3\) در عدد \(\Large 84\) توانی ندارد، توان آن را برابر با \(\Large 1\) در نظر می‌گیریم). بنابراین ب.م.م دو عدد برابر است با:

\(\LARGE  (72,84)=2^2 \times 3 =12 \)

برای به دست آوردن ک.م.م دو عدد باید هم پایه‌های مشترک و هم غیر مشترک را با بیشترین توان در هم ضرب کنیم. پایهٔ \(\Large 2\) در هر دو عدد مشترک است و بیشترین توان آن در عدد \(\Large 72\) وجود دارد و برابر با \(\Large 3\) است. پایهٔ \(\Large 3\) نیز، در هر دو عدد مشترک است و بیشترین توان آن در عدد \(\Large 72\) وجود دارد و برابر با \(\Large 2\) است. پایهٔ \(\Large 7\) مشترک نیست و تنها در عدد \(\Large 84\) وجود دارد. بیشترین توان آن نیز برابر با \(\Large 1\) است. بنابراین ک.م.م دو عدد برابر است با:

\(\Large [72,84]=2^3 \times 3^2 \times 7 =504\)

به قسمت بعدی از درسنامهٔ تعریف توان ریاضی هفتم دقت کنید.

کاربرد توان در حل مسائل

در حل مسائل مختلف نیز می‌توان از مفهوم توان کمک گرفت. به مثال زیر دقت کنید.

مثال 3: ضخامت یک مقوا، \(\Large 1\) میلی‌متر است. اگر آن را 10 بار تا بزنیم، ضخامت مقوای تا شده را با استفاده از توان نمایش دهید؟

حل: هر بار که مقوا را تا می‌زنیم، ضخامت آن دو برابر می‌شود. اگر یک بار آن را تا کنیم، ضخامت آن \(\Large 2\) میلی‌متر خواهد شد. اگر \(\Large 2\) بار تا بزنیم، ضخامت مقوای تا شده، \(\Large 2 \times 2\) یا همان \(\Large 2^2\) میلی‌متر خواهد شد. به همین ترتیب می‌توان فهمید که اگر \(\Large 10\) بار مقوا را تا کنیم، ضخامت مقوای تا شده برابر با \(\Large 2^{10}\) میلی‌متر می‌شود.

برای خوندن مطلب به پست محاسبه عبارت تواندار مراجعه کنید.

زنگ آخر کلاس تعریف توان ریاضی هفتم

در درسنامه‌ای که از ریاضی هفتم خواندیم، ابتدا با مفهوم توان آشنا شدیم. سپس کاربرد توان در محاسبهٔ مساحت مربع و دایره و همچنین تجزیهٔ اعداد را بررسی کردیم. همان طور که دیدید، تجزیهٔ اعداد به شمارنده‌های اول با استفاده از مفهوم توان به ما در یافتن ب.م.م و ک.م.م نیز کمک می‌کرد. 

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با تعریف توان ریاضی هفتم دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.