آموزش ریاضی پایه هفتم
بزرگترین شمارنده مشترک ریاضی هفتم ✳️📖 – ب.م.م پیدا کن!
در درسنامۀ بزرگترین شمارنده مشترک ریاضی هفتم ، روش به دست آوردن ب.م.م دو عدد را نشان میدهیم. همچنین، علاوه بر پیدا کردن ب.م.م اعداد مختلف، کاربرد محاسبۀ ب.م.م دو عدد در حل مسائل مختلف را نیز خواهیم دید.
بزرگترین شمارنده مشترک یا ب.م.م
بزرگترین شمارنده ی مشترک دو عدد چیست؟ از اسمش کاملاً پیداست. اگر تعدادی عدد و شمارندههایشان را داشته باشیم، برخی از شمارندهها بین آنها مشترک هستند. یعنی دقیقاً به نعداد یکسان در حاصل ضرب همۀ آن عددها وجود دارند. بزرگترینشان همان بزرگترین شمارنده مشترک است. مثلاً دو عدد \(\Large 4\) و \(\Large 6\) را در نظر بگیرید. تمام شمارندههای این دو عدد را مینویسیم:

اعداد \(\Large 1\) و \(\Large 2\)، شمارندههای مشترک هر دو عدد هستند. به همین خاطر آنها را با رنگ قرمز مشخص کردهایم. عدد \(\Large 2\) بزرگترین شمارندۀ مشترک دو عددِ \(\Large 4\) و \(\Large 6\) است. دقت کنید، هرعدد طبیعی بر \(\Large 1\) بخش پذیر است. بنابراین هر دو عددی حداقل یک شمارندۀ مشترک دارند که همان عدد \(\Large 1\) است.
به بزرگترین شمارنده مشترک دو عدد طبیعی \(\Large a\) و \(\Large b\)، ب.م.م (بخوانید بِ میم میم) دو عدد \(\Large a\) و \(\Large b\) نیز میگوییم و آن را با نماد \(\Large (a, b)\) نشان میدهیم. اما دلیل این نام گذاری چیست؟ عدد \(\Large a\) را در نظر بگیرید. به اعدادی که باقیماندۀ تقسیم عدد \(\Large a\) بر آنها صفر باشد، شمارندههای عدد \(\Large a\) میگوییم. اگر \(\Large a\) را بر یک عدد تقسیم کنیم، آن عدد مقسومٌ علیه نامیده میشود. از این رو به شمارندههای هر عدد، مقسوم علیههای آن نیز میگوییم. بنابراین بزرگترین شمارنده مشترک دو عدد را بزرگترین مقسوم علیه مشترک دو عدد نامیده و به اختصار به آن ب.م.م میگوییم. در قسمت بعدی از درسنامۀ بزرگترین شمارنده مشترک ریاضی هفتم روش یافتن ب.م.م دو عدد را بررسی میکنیم.
روش یافتن ب.م.م دو عدد
دو روش کلی برای یافتن بزرگترین شمارنده مشترک دو عدد وجود دارد:
- نوشتن تمام شمارندههای دو عدد
- تجزیۀ دو عدد به شمارندههای اول
هر کدام از این دو روش را در دو قسمت جداگانه معرفی کرده و از هر یک، مثالهایی حل میکنیم.
پیدا کردن ب.م.م با نوشتن تمام شمارنده ها
از این روش، در ابتدای درسنامه برای پیدا کردن ب.م.م دو عدد \(\Large 4\) و \(\Large 6\) استفاده کردیم. تمام شمارندههای هر عدد را نوشتیم. شمارنده های مشترک را پیدا کردیم. در نهایت، بزرگترینشان همان ب.م.م دو عدد بود. در مثال بعدی از درسنامۀ بزرگترین شمارنده مشترک ریاضی هفتم ب.م.م دو عدد دیگر را به همین روش پیدا میکنیم.
مثال از پیدا کردن ب.م.م با نوشتن تمام شمارنده ها
مثال 1: ب.م.م دو عدد \(\Large 18\) و \(\Large 30\) را با نوشتن تمام شمارندههای دو عدد بیابید.
حل: ابتدا تمام شمارندههای دو عدد را مینویسیم:

اعداد \(\Large 1\) و \(\Large 2\) و \(\Large 3\) و \(\Large 6\)، شمارندههای مشترک دو عدد هستند. به همین خاطر آنها را با رنگ قرمز نشان دادهایم. بزرگترینشان، عدد \(\Large 6\) است. بنابراین ب.م.م دو عدد \(\Large 18\) و \(\Large 30\) برابر با \(\Large 6\) است. همان طور که گفتیم میتوانیم از نماد \(\Large (18, 30)=6\) نیز استفاده کنیم. در قسمت بعدی از درسنامۀ بزرگترین شمارنده مشترک ریاضی هفتم روش دوم یافتن ب.م.م دو عدد را معرفی میکنیم.
پیدا کردن ب.م.م با تجزیۀ اعداد
در درسنامۀ شمارنده اول، روش تجزیۀ اعداد و پیدا کردن شمارندههای اول یک عدد را آموختیم. اگر دو عدد را به صورت حاصل ضرب شمارندههای اول بنویسیم، حاصل ضرب قسمتهای مشترک دو عدد، همان ب.م.م است. البته این جمله دقیق نیست؛ اما چون هنوز با مفهوم توان آشنا نشدهاید، مجبوریم از این عبارت استفاده کنیم. با استفاده از مفهوم توان میتوان این روش را به این صورت بیان کرد: ب.م.م چند عدد برابر است با حاصل ضرب شمارندههای مشترک بین تمام آنها با کوچکترین توان. برای اینکه بهتر متوجه شوید، به مثال زیر از درسنامۀ بزرگترین شمارنده مشترک ریاضی هفتم توجه کنید
مثال از پیدا کردن ب.م.م با تجزیۀ اعداد
مثال 2: ب.م.م دو عدد \(\Large 42\) و \(\Large 66\) را با تجزیۀ دو عدد به شمارندههای اول بیابید.
حل: ابتدا با استفاده از نمودار درختی، دو عدد را به شمارندههای اول تجزیه میکنیم (در صورتی که روش رسم نمودار درختی را فراموش کردهاید، درسنامۀ شمارنده اول را مرور کنید):
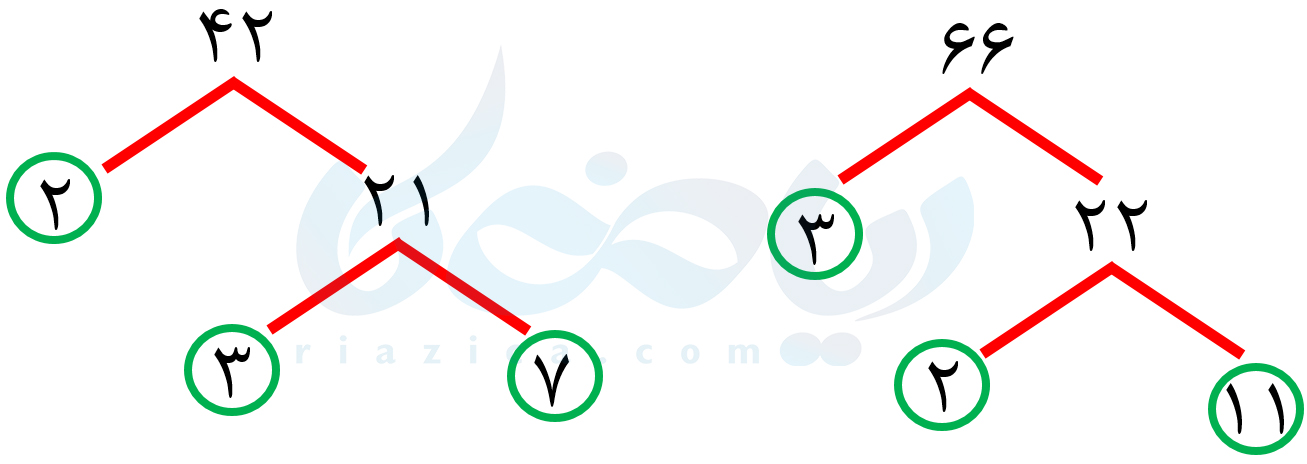
با توجه به دو نمودار بالا، دو عدد \(\Large 42\) و \(\Large 66\) را میتوانیم به صورت زیر بنویسیم:
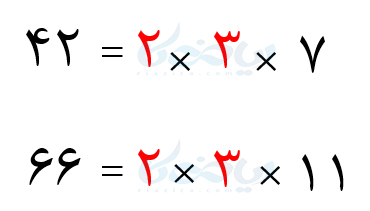
قسمتهای مشترک دو عدد را با رنگ قرمز مشخص کردهایم. با توجه به توضیحی که دادیم، ب.م.م دو عدد برابر است با حاصل ضرب قسمتهای مشترک. بنابراین داریم:
\(\LARGE (42, 66)=2 \times 3=6\)
استفاده از مفهوم توان
همین مثال (مثال 2) از درسنامۀ بزرگترین شمارنده مشترک ریاضی هفتم را میتوان با استفاده از مفهوم توان به این صورت حل کرد:
شمارندههای \(\Large 2\) و \(\Large 3\) بین دو عدد مشترک هستند و کمترین توان هر یک برابر است با \(\Large 1\). در نتیجه ب.م.م دو عدد برابر است با:
\(\LARGE (42, 66)=2 \times 3=6\)
به مثال بعدی از درسنامۀ بزرگترین شمارنده مشترک ریاضی هفتم توجه کنید
پیدا کردن ب.م.م سه عدد با تجزیۀ اعداد
مثال 3: حاصل \(\Large (24, 36, 84)\) را با تجزیۀ سه عدد به شمارندههای اول بیابید.
حل: برای به دست آوردن ب.م.م سه یا چند عدد نیز میتوانیم از روش اول یا دوم استفاده کنیم. با توجه به خواستۀ مسئله، از روش دوم استفاده میکنیم. ابتدا سه عدد داده شده را تجزیه میکنیم:
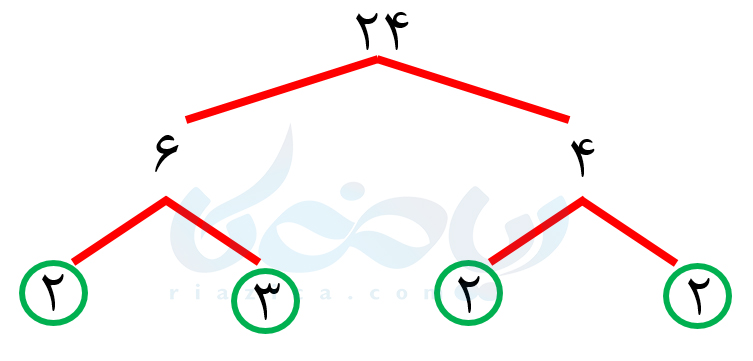
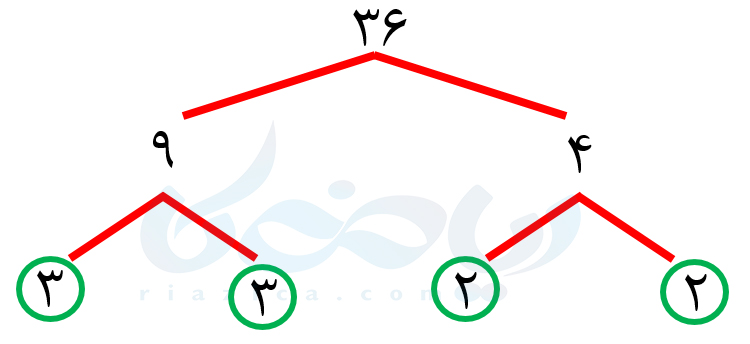
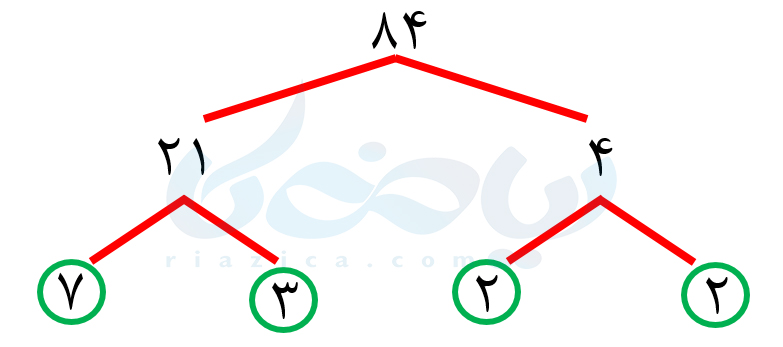
با توجه به نمودارهای بالا، سه عدد \(\Large 84\) و \(\Large 36\) و \(\Large 24\) را میتوانیم به صورت زیر بنویسیم:
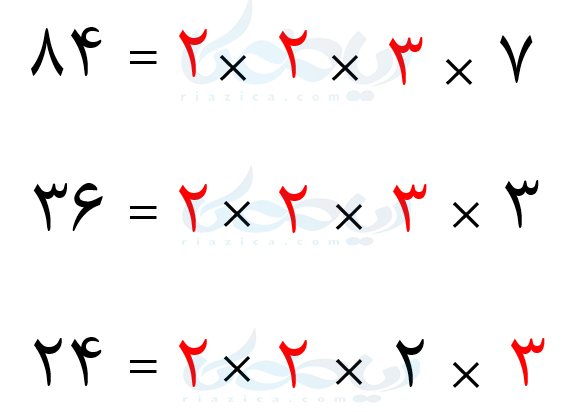
قسمتهای مشترک سه عدد را با رنگ قرمز مشخص کردهایم. با توجه به توضیحی که دادیم، ب.م.م اعداد داده شده برابر است با حاصل ضرب قسمتهای مشترک. بنابراین داریم:
\(\Large (24, 36, 84)=2 \times 2 \times 3=12\)
استفاده از مفهوم توان
همین مثال (مثال 3) از درسنامۀ بزرگترین شمارنده مشترک ریاضی هفتم را میتوان با استفاده از مفهوم توان به صورت زیر حل کرد:
ابتدا سه عدد \(\Large 84\) و \(\Large 36\) و \(\Large 24\) را به صورت زیر تجزیه میکنیم:
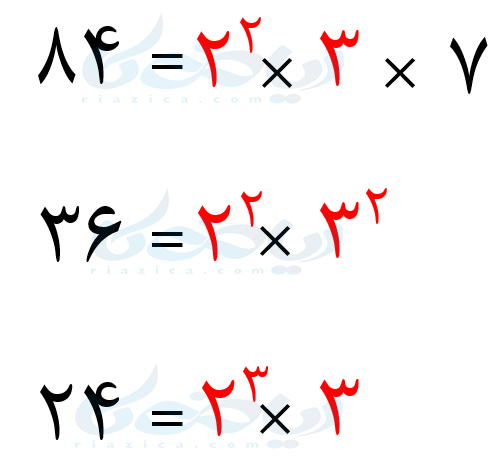
شمارندۀ \(\Large 2\) بین هر سه عدد مشترک است و کمترین توان آن برابر است با \(\Large 2\). شمارندۀ \(\Large 3\) نیز بین هر سه عدد مشترک است و کمترین توان آن برابر است با \(\Large 1\). در نتیجه داریم:
\(\Large (24, 36, 84)=2^2 \times 3=12\)
نکات کلیدی در مورد ب.م.م اعداد
۱-ب.م.م دو عدد اول عدد یک می باشد.مثال:\(\LARGE (3,11)=1 \)
۲-ب.م.م یک عدد اول مانند a با یک عدد غیر اول مانند b یا یک می شود یا خود عدد اول a.مثال: \(\LARGE (9, 3)=3\) یا \(\LARGE (12, 5)=1\)
۳- اگر دو عدد به هم بخش پذیر باشند ب.م.م آنها می شود عدد کوچکتر . مثال: \(\LARGE (22,11)=11 \)
۴-ب.م.م هر عدد با یک می شود یک . \(\LARGE (n,1)=n \)
۵- ب.م.م هر عدد با خودش می شود خودش. \(\LARGE (n,n)=n \)
کاربرد محاسبۀ ب.م.م در حل مسائلn
در صورت بعضی از مسائل به طور مستقیم از ما خواسته نشده که ب.م.م چند عدد را محاسبه کنیم، اما برای حل انها لازم است تا چنین محاسبهای انجام شود. برای اینکه با این دسته از مسائل بیشتر آشنا شوید، در ادامۀ درسنامۀ بزرگترین شمارنده مشترک ریاضی هفتم دو نوع از این مسائل را حل خواهیم کرد.
مثال از کاشی کاری استخر
مثال 4: میخواهیم یک استخر با ابعاد \(\Large 24\) و \(\Large 88\) را با استفاده از کاشیهای مربع شکل یک اندازه، کاشی کاری کنیم. برای این کار، حداقل و حداکثر به چه تعداد کاشی نیاز داریم؟
حل: از آنجاییکه کاشیها مربع شکل هستن، طول و عرض آنها برابر است. بنابراین ضلع کاشی، هم باید شمارندۀ \(\Large 24\) باشد و هم شماندۀ \(\Large 88\). شمارندههای هر دو عدد \(\Large 24\) و \(\Large 88\) را مینویسیم:

همان طور که میبینید، اعداد \(\Large 1\) و \(\Large 2\) و \(\Large 4\) و \(\Large 8\)، شمارندههای مشترک دو عدد \(\Large 24\) و \(\Large 88\) هستند. بنابراین تنها میتوانیم از کاشیهای به ضلع \(\Large 1\) یا \(\Large 2\) یا \(\Large 4\) یا \(\Large 8\) استفاده کنیم. اگر بخواهیم از حداقل کاشیهای ممکن برای کاشی کاری استخر استفاده کنیم، باید بزرگترین ابعاد ممکن را برای کاشیهای مربعی شکل در نظر بگیریم. یعنی باید از کاشیهای مربع شکل به ضلع \(\Large 8\) استفاده کنیم. در این صورت با تقسیم مساحت استخر بر مساحت هر کاشی، حداقل تعداد کاشی مورد نیاز به صورت زیر به دست میآید:
\(\LARGE \frac{24 \times 88}{8 \times 8}=33\)
اما اگر بخواهیم از حداکثر تعداد کاشی ممکن استفاده کنیم، باید کوچکترین ابعاد ممکن را برای کاشیهای مربع شکل در نظر بگیریم. یعنی باید از کاشیهایی به ضلع \(\Large 1\) استفاده کنیم. در این صورت، حداکثر کاشی مورد نیاز به صورت زیر به دست میآید:
\(\LARGE \frac{24 \times 88}{1 \times 1}=2112\)
به مثال بعدی از درسنامۀ بزرگترین شمارنده مشترک ریاضی هفتم توجه کنید.
مثال از بزرگترین شمارنده مشترک ریاضی هفتم
مثال 5: یخدانی به طول \(\Large 42\)، عرض \(\Large 28\) و ارتفاع \(\Large 70\) داریم. میخواهیم درون این یخدان را با یخهای مکعب شکل یکسان کاملاً پر کنیم. برای این کار حداقل به چند یخ نیاز داریم؟
حل: از آنجاییکه یخها مکعب شکل هستند، طول و عرض و ارتفاع آنها برابر است. بنابراین طول هر یخ، هم باید شمارندۀ \(\Large 42\) باشد، هم شماندۀ \(\Large 28\) و هم شمارندۀ \(\Large 70\). از طرفی، چون به دنبال کمترین تعداد یخ هستیم، باید ب.م.م این سه عدد را پیدا کنیم. هر یک از اعداد \(\Large 42\) و \(\Large 28\) و \(\Large 70\) را با استفاده از نمودار درختی تجزیه کردیم:
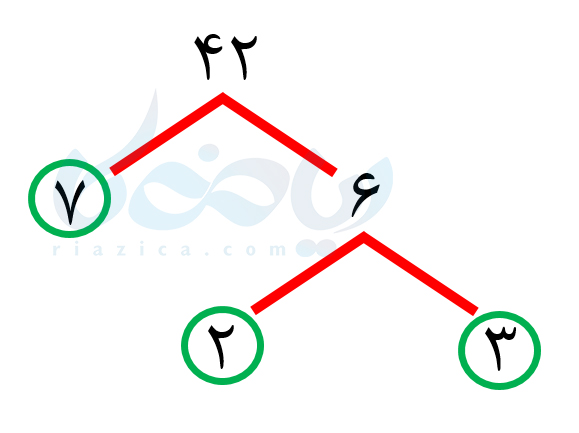
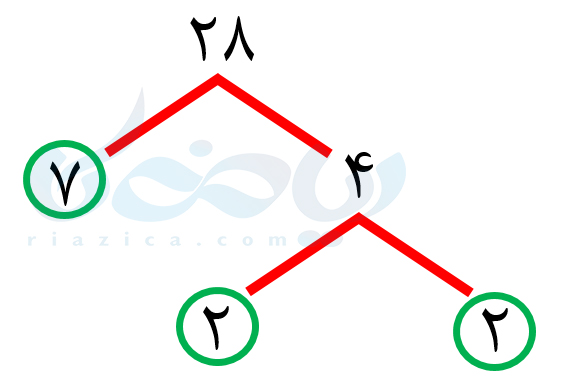
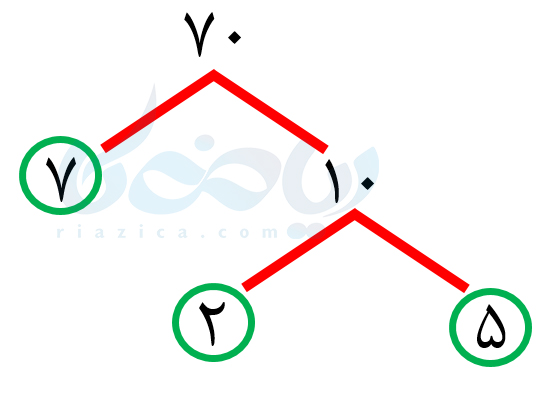
با توجه به نمودارهای بالا، میتوانیم سه عدد \(\Large 42\) و \(\Large 28\) و \(\Large 70\) را به صورت زیر بنویسیم:
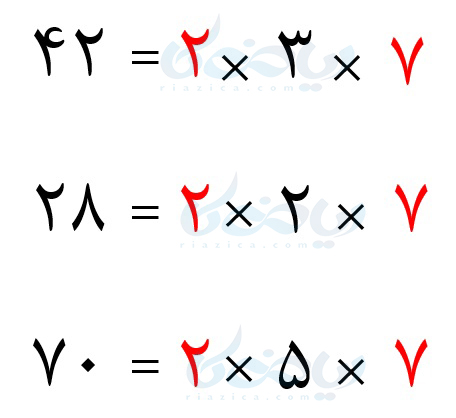
قسمتهای مشترک سه عدد را با رنگ قرمز مشخص کردهایم. ب.م.م اعداد داده شده برابر است با حاصل ضرب قسمتهای مشترک. بنابراین داریم:
\(\LARGE (42, 28, 70)=2 \times 7=14\)
بنابراین باید از یخهای مکعب شکل به طول \(\Large 14\) استفاده کنیم. تعداد یخهای مورد نیاز از تقسیم حجم مکعب بر حجم هر یخ به صورت زیر به دست میآید:
\(\LARGE \frac{42\times 28 \times 70}{14 \times 14 \times 14}=30\)
قبل از خوندن این پست توصیه میشه پست های عدد اول ریاضی هفتم وشمارنده اول ریاضی هفتم رومطالعه کنی و در ادامه پست کوچکترین مضرب مشترک ریاضی هفتم رو هم بخونی.
زنگ آخر کلاس بزرگترین شمارنده مشترک ریاضی هفتم
همانطور که در این درسنامه از ریاضی هفتم دیدید، دو روش برای به دست آوردن ب.م.م اعداد وجود دارد. اولین روش، نوشتن تمام شمارندههای هر عدد و پیدا کردن بزرگترین شمارندۀ مشترک است. دومین روش، تجزیۀ اعداد و محاسبۀ حاصل ضرب قسمتهای مشترک اعداد داده شده است. در طول درسنامه سعی کردیم با حل مثالهای مختلف در درک بهتر این مبحث به شما کمک کنیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با این مبحث دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





خيلى ممنونم توضيحاتتون عالى بود
با سلام وعرض ادب
ممنون از توجه شما
بسیار عالی، من و پسرم بسیار استفاده کردیم.
با سلام وروز به خیر
بسیار خرسندیم که براتون مفید بوده
به شکرانه از زحمات شما چی باید بگم؟
با سلام وعرض ادب
ممنون از شما کاری جز همین نظر محبت شما لازم نیست
با سلام و عرض ادب خدمت شما دبیر ارزشمند.بسیار عالی توضیح دادید برایه من بسیار مفید بود خدا اجرتون بده
با سلام وعرض ادب
خوشحالیم که مفید واقع شده
بسیار عالی توضیحات جامع و کامل…ممنون
عالی
با سلام وادب
ممنون دوست عزیز
باسلام دوستان خیلی قشنگ توضیع مدند
با سلام وادب
ممنون از دلگرمی شما
وب بود
سلام ممنونم عالی بود
با سلام وادب
ممنون از نگاه شما
با سلام واقعا عالی مفهوم را برای دانش آموزان توضیح دادید ممنون عزیز جان
عالی بود
با سلام وادب
ممنون از نگاه شما
سلام،
خیلی خیلی ممنون
ان شاء الله عاقبت بخیر شوید
سلام ممنون از دعای خیر شما
عالی