آموزش ریاضی پایه هشتم
حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
ترتیبی که برای خواندن درسنامههای آموزش ریاضی هشتم به شما پیشنهاد میدهیم:
- زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعیها!
- اعداد صحیح ↔️➖➕– نمایش روی محور مختصات
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعیها!
- تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
- عدد اول ریاضی هشتم 1️⃣👨🎓 – کاملترین آموزشی که لازم داشتید.
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- خط و دایره : از سیر ➖ تا پیاز 🔴
- خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خطها در چهارراه زاویه!
- چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!
- ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
- فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارتهای جبری استفاده کن!
- حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
- بردار و مختصات ریاضی هشتم ➡️⬅️ – جهتدار و کامل!
- بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
- شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
- مثلث های هم نهشت 🌷🔺 گل سرسبد شکلهای همنهشت!
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
- همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد میگیرید
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!
با حل معادله کارآگاه میشی! یه سری چیزها معلوم و یه سری چیزها مجهول هستن که با ترفندهای کارآگاهی این درس حلش میکنی… . در درس حل معادله درجه اول از مجموعه آموزش ریاضی پایه هشتم ، ابتدا معادله و اجزای تشکیلدهنده آن را تعریف کرده و با معادلات درجه اول آشنا میشویم. در ادامه با راهحل گام به گام، میتوانیم معادله درجه اول را در دو حالت کسری و غیر کسری حل کنیم. در پایان چندین مثال طبقهبندی شده ارائه شده است تا خیالتان بابت یادگیری این درس راحت باشد!
تعاریف مربوط به معادله
در ریاضیات پایه هفتم (فصل 3) با مفهوم معادله آشنا شدیم. برای مرور مطالب سال قبل و آمادگی برای حل معادله درجه اول ، ابتدا با چند تعریف آشنا خواهیم شد:
معادله چیست؟
معادله، یک تساوی جبری است که به ازای مقدار یا مقادیری ، تبدیل به یک تساوی صحیح میشود. به عنوان نمونه به معادله زیر توجه کنید:
\( \Large 4x – 3 = 2x + 9 \)
به زبان خیلی ساده: یک علامت تساوی داریم که دو طرف آن، حروف انگلیسی (بهش میگیم متغیر یا مجهول) و عددها قرار دارند. چه زمانی علامت تساوی صحیح است؟ وقتی عددی که به جای مجهولات قرار میدهیم، باعث تساوی دو طرف شود.
مثلاً بیایید در تساوی جبری زیر، اعداد 2 و 3 را امتحان کنیم: (فراموش که نکردید چگونه مقدار یک عبارت جبری را در درسنامه فاکتورگیری پیدا میکردیم؟)
\( \Large 2 x – 1 = 5 \)
\( \Large 2 (×2) – 1 = 4 – 1 = 3 \) (جایگذاری عدد 2)
\( \Large 2 (×3) – 1 = 6 – 1 = 5 \) (جایگذاری عدد 3)
سمت چپ تساوی، برای عدد 2 برابر با 3 و برای عدد 3 برابر با 5 شده است؛ پس برای \( \Large x=3 \) تبدیل به یک تساوی صحیح شده است.ما این معادله را به روش حدس وگمان حل کردیم اما می خواهیم روش کلی حل معادله درجه دوم را فرا بگیریم.
مجهول، ضریب مجهول و اعداد معلوم
منظور از اعداد معلوم، همان عددهای صحیح، کسری، اعشاری و … است که داریم (مانند \( \Large 1 \)، \( \Large 2 \)، \( \Large (-1) \)، \( \LARGE \frac {2}{3} \) و …).
مجهول، بصورت حرف انگلیسی نشان داده میشود و قرار است با حل معادله درجه اول ، مقدار آن را بدست آوریم.
ضریب مجهول، عددی است که در مجهول ضرب شده است. در معادله زیر، این موارد نشان داده شده است:

مثال 1: در معادله زیر، مجهول، ضریب مجهول و اعداد معلوم را مشخص کنید.
\( \Large 6 a = -3 \)
حل 1:
در این معادله، \( \Large a \) مجهول، عدد 6 ضریب مجهول و عدد (3-) عدد معلوم است.
معادله درجه اول
اگر در معادلهای بزرگترین توان مجهول برابر با (1) باشد، آن معادله را معادله درجه اول میگویند. این معادله بصورت \( \Large a x + b = c \) نوشته میشود.
نکته: نوع معادلات درجه دوم و بالاتر نیز بر اساس بزرگترین توان مجهول معادله تعیین میشود؛ به عنوان نمونه چند معادله با درجات مختلف را میتوانید مشاهده نمایید:
\( \Large 5 x + 4 = 0 \) (معادله درجه اول)
\( \LARGE \frac {1}{3} x + x^2 = -5 \) (معادله درجه دوم)
\( \Large 6x^{11} – x^6 = 5x^9 + 1 \) (معادله درجه یازدهم)
یکی از کاربردهای معادله درجه اول، معادله خط است. معادلات درجه دو و روش حل آنها را نیز در پایههای بالاتر یاد خواهید گرفت.
حل معادله درجه اول
به طور کلی در جبر و معادله ریاضیات پایه هشتم، برای حل معادله درجه اول ، دو حالت وجود دارد:
- معادله درجه اول، غیر کسری است؛ یعنی ضرایب مجهول و اعداد معلوم اعدادی صحیح هستند. (مانند معادله \( \Large -2 x + 6 = -3 \) ).
- معادله درجه اول، کسری است؛ یعنی حداقل یکی از ضرایب مجهول و اعداد معلوم عددی کسری باشد. (مانند معادله \( \LARGE 1 + \frac {2}{5}x = -\frac {6}{25} \) ).
حل معادله درجه اول غیر کسری
برای حل معادله درجه اول ، گام به گام طبق مراحل زیر پیش میرویم:
- مجهولها را به سمت چپ و اعداد معلوم را به سمت راست تساوی منتقل میکنیم. (دقت کنید! عددی که به طرف دیگر تساوی منتقل شود، تغییر علامت میدهد)؛
- مجهولها را با هم و معلومها را با هم جمع و تفریق میکنیم؛
- حاصل معلومها را بر حاصل ضرایب مجهول تقسیم میکنیم. (به همین سادگی! جواب معادله بدست آمد).
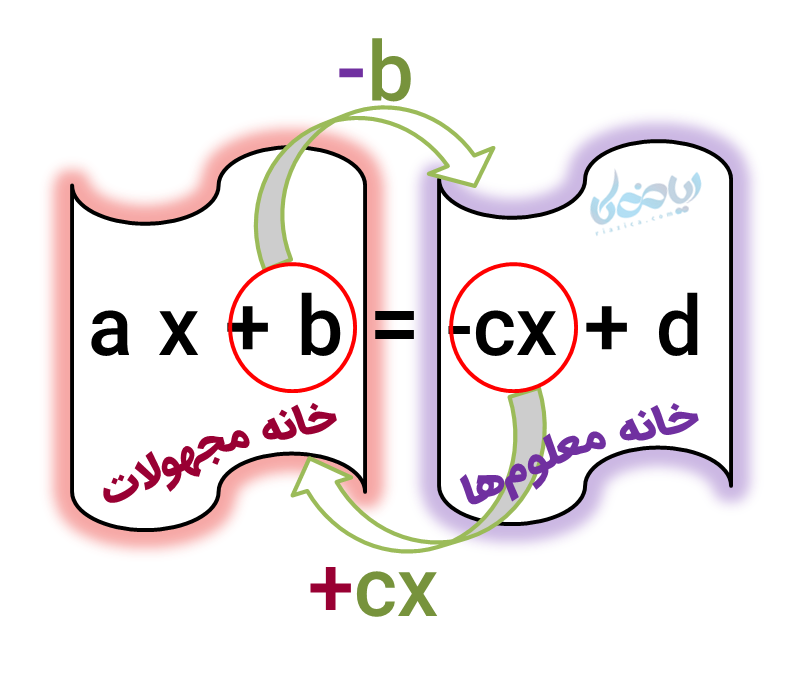
مثال 2: با حل معادله زیر، مقدار \( \Large x \) را بدست آورید.
\( \Large 3x – 3 = x + 5 \)
حل 2:
این معادله غیر کسری است، پس طبق مراحل روش حل معادله درجه اول عمل میکنیم:
مجهول این معادله، \( \Large x \) است؛ پس باید \( \Large 3x \) و \( \Large x \) در سمت چپ تساوی باشند. اعداد معلوم این معادله، 5 و (3-) هستند که باید در سمت راست تساوی قرار بگیرند.
امّا حتما باید دقت کنیم که علامت \( \Large x \) وقتی به سمت چپ منتقل شود عوض میشود (یعنی -) و علامت (3-) وقتی به طرف راست برده شود، عوض میشود (یعنی +):
\( \Large 3x – x = (+3) + 5 \)
سپس مجهولات را با هم و معلومها را با هم جمع میکنیم:
\( \Large 2x = 8 \)
مرحله آخر، تقسیم عدد معلوم (8) به ضریب مجهول (2) است:
\( \LARGE x = \frac {8}{2} = 4 \)
حل معادله درجه اول کسری
در صورتی که معادله درجه اول کسری باشد، باید ابتدا آن را به حالت غیر کسری تبدیل کنیم. سپس از همان روش بالا معادله را حل کنیم؛ پس مراحل زیر را طی میکنیم:
- دو طرف معادله را در (ک.م.م) مخرجها ضرب میکنیم (یادآوری : ک.م.م ریاضی هفتم)؛ معادله کسری تبدیل به معادله غیر کسری میشود.
- از روش حل معادله درجه اول غیر کسری ، آن را حل میکنیم.
مثال 3: معادله زیر را حل کنید.
\( \LARGE – \frac {6}{25} x + \frac {4}{15} = \frac {8}{3} \)
حل 3:
این معادله، از نوع درجه اول کسری است، پس ابتدا باید (ک.م.م) مخرج کسرها (یعنی 25، 15 و 3) را محاسبه کرده (75) و در کل جملات ضرب کنیم:
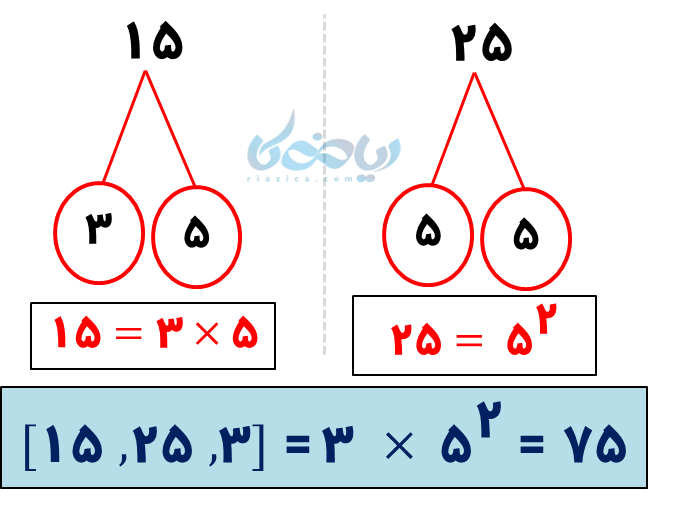
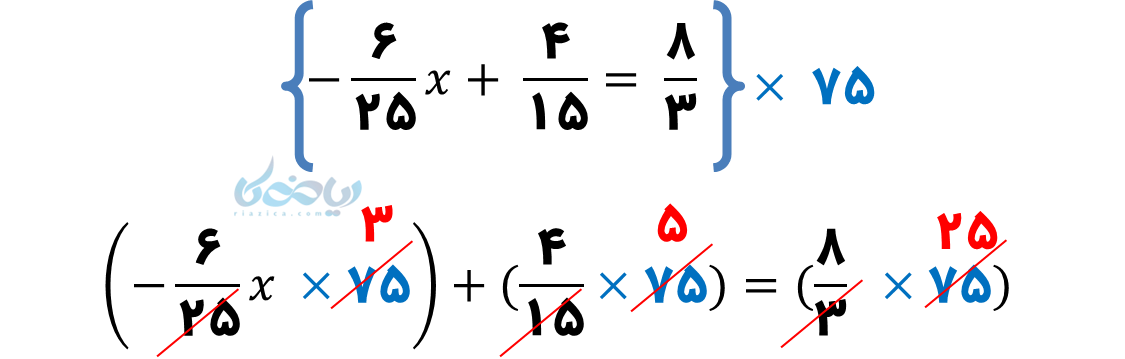
\( \Large – 18 x + 20 = 200 \)
که این معادله غیر کسری را میتوان با استفاده از روش حل معادله درجه اول مرحله به مرحله حل کرد:
در این معادله یک عبارت دارای مجهول وجود دارد و سمت چپ تساوی است، پس لازم نیست آن را منتقل کنیم؛ اما عدد معلوم (20+) را به سمت راست منتقل میکنیم (با تغییر علامت):
\( \Large – 18 x = 200 – 20 = 180 \)
حاصل مجهولات و حاصل اعداد معلوم بدست آمده است. با تقسیم عدد معلوم (180) به ضریب مجهول (18-) جواب معادله بدست میآید:
\( \LARGE x = \frac {180}{-18} = -10 \)
آیا همیشه در حل معادله درجه اول یک جواب بدست میآید؟
معادلات بدون جواب
بعضی از معادلهها هیچ جوابی ندارند؛ این حالت در شرایطی اتفاق میافتد که از دو طرف معادله به یک جواب غلط میرسیم. به معادله زیر توجه کنید:
\( \LARGE 5x – 6 = x + 7 + 4x \)
\( \LARGE → 5x – 6 = 5x + 7 \)
اگر عبارت \( 5x \) را از دو طرف خط بزنیم، خواهیم داشت:
\( \LARGE → – 6 = 7 \)
که یک عبارت غلط است. پس هیچ عددی یافت نمی شود که به جای \( x \) در معادله قرار دهیم و تساوی برقرار شود. پس این معادله جواب ندارد.
معادلات دارای بینهایت جواب
بعضی از معادلهها هم هستند که بینهایت جواب دارند؛ این حالت در شرایطی اتفاق میافتد که مجهول حذف شود ودر دو طرف معادله به جوابی برسیم که همیشه درست است. معادله زیر را با هم ببینیم:
\( \LARGE 4 – 2x = -2x + 4 \)
اگر عبارت \( -2x \) را از دو طرف خط بزنیم، خواهیم داشت:
\( \LARGE → 4 = 4 \)
این عبارت همیشه صحیح است. پس هر عددی به جای \( x \) در معادله قرار دهیم تساوی برقرار میشود. این یعنی معادله مورد نظر بینهایت جواب دارد،یا به عبارتی مجموعه جواب آن ،مجموعه اعداد حقیقی می باشد.
چند مثال از حل معادله درجه اول
مثال 4: طول مستطیلی 20 سانتیمتر و محیط آن 50 سانتیمتر است؛ عرض این مستطیل را بدست آورید.
حل 4:
میدانیم محیط مستطیل 2 برابر مجموع طول و عرض آن است. این عبارت را میتوان بصورت جبری بدین صورت نوشت:
\( \Large 2 × (20 + x) = 50 \)
مجهول این مسأله، عرض مستطیل یعنی \( \Large x \) است، پس با حل معادله درجه اول جواب سؤال بدست خواهد آمد. عدد 2 را در پرانتز ضرب میکنیم:
\( \Large 40 + 2x = 50 \)
باید عددهای معلوم را به سمت راست و مجهول را به سمت چپ منتقل کنیم؛ \( \Large 2x \) در سمت چپ قرار دارد، پس نیازی به انتقال آن نیست، اما عدد 40 را به سمت راست میبریم و حاصل اعداد معلوم را مینویسیم:
\( \Large 2x = 50 – 40 = 10 \)
حال با تقسیم عدد معلوم (10) بر ضریب مجهول (2)، جواب این معادله (عرض مستطیل) بدست میآید:
\( \LARGE x = \frac {10}{2} = 5 \)
مثال 5: پدری 45 سال سن دارد. دو فرزند او 9 و 14سالهاند. پس از چند سال سن پدر با مجموع سن فرزندانش برابر میشود؟
حل 5:
بیایید تعداد سالهایی را که میگذرد تا سن پدر با مجموع سن فرزندانش برابر شود، \( \Large x \) در نظر بگیریم. بنابراین \( \Large x \) به سن تک تک آنها اضافه میشود. تساوی جبری جملهای که گفتیم، بدین صورت است:
\( \Large 45 + x = (9+x) + (14+x) \)
طبق روش حل معادله درجه اول ، مجهولات را به سمت چپ و معلومها را به سمت راست تساوی منتقل کرده و حاصلجمع هریک را محاسبه میکنیم:
\( \Large x –x –x = 9+ 14 -45 \)
\( \Large -x = -22 \)
با تقسیم عدد معلوم (22-) بر ضریب مجهول (1-)، مشخص میشود که پس از 22 سال این اتفاق خواهد افتاد:
\( \LARGE x = \frac {-22}{-1} = 22 \)
حل یک مثال فیزیکی
مثال 6: در فیزیک الکتریسیته، اختلاف پتانسیل از رابطه \( \Large V = R × I \) بدست میآید که در آن \( \Large V \) اختلاف پتانسیل، \( \Large R \) مقاومت الکتریکی و \( \Large I \) جریان الکتریکی را نشان میدهد. اگر در یک مدار، مقاومت برابر با \( \LARGE \frac {1}{2} \) اُهم و اختلاف پتانسیل 4 ولت باشد، چه جریانی از آن عبور میکند؟
حل 6:
با جایگذاری اعداد داده شده در صورت سؤال، در رابطه داده شده برای اختلاف پتانسیل خواهیم داشت:
\( \LARGE 4 = \frac {1}{2} × I \)
که معادلهای درجه اول است با متغیر \( \Large I \)؛ دقت کنید که این معادله کسری است و باید ابتدا آن را در (ک.م.م) مخرجها ضرب کنیم. مخرج عدد 4، برابر است با 1 (چون عدد طبیعی است)؛ پس (ک.م.م) اعداد 1 و 2 (که برابر است با 2) در کل جملات ضرب میکنیم:
\( \Large 8 = I \)
عدد معلوم (8) را به سمت راست و مجهول (\( \Large I \)) را به سمت چپ منتقل میکنیم:
\( \Large -I = -8 \)
با تقسیم عدد معلوم (8-) به ضریب مجهول (1-) مقدار مجهول (جریان الکتریکی) بدست میآید:
\( \Large I = \frac {-8}{-1} = 8 \) آمپر
توجه: در این مثال میتوانستیم از همان عبارت \( \Large 8 = I \) نتیجه بگیریم که \( \Large I = 8 \) و نیازی به دو مرحله بعد نبود؛ چون در واقع فرقی ندارد مجهولات سمت چپ باشند یا راست. ما روش گام به گام را به عنوان یک قرارداد گفتیم.
حل یک مثال ترکیبی
مثال 7: با حل معادله زیر، مقدار \( \Large x \) را بدست آورید.
\( \Large x(x^3-4)+2x-x^4=5x+1 \)
حل 7:
- شاید با دیدن این معادله وحشت کنید و با حالت اعتراض بگویید: «این که حل معادله درجه اول نیست!» اما کمی صبر کنید. بیایید طبق روشی که در درس ساده کردن عبارتهای جبری یاد گرفتهایم، معادله را کمی سادهتر کنیم. ابتدا با ضرب \( \Large x \) در پرانتز شروع میکنیم:
\( \Large x^4-4x+2x-x^4=5x+1 \)
جملات متشابه را طبق روش درس ساده کردن عبارتهای جبری با هم جمع میکنیم :
\( \Large (x^4-x^4)+(-4x+2x)=5x+1 \)
\( \Large -2x=5x+1 \)
این عبارت طولانی و به ظاهر پیچیده، تبدیل به یک معادله درجه اول شد؛ پس مجهولات را سمت چپ و معلومها را سمت راست مینویسیم و حاصل را بدست میآوریم:
\( \Large -2x – 5x =1 \)
\( \Large -7x =1 \)
حال عدد معلوم (1) را بر ضریب مجهول (7-) تقسیم میکنیم:
\( \LARGE x = \frac {1}{-7} = – \frac {1}{7} \)
مثالهایی در مورد جمع اعداد متوالی
معمولاً از این درس سؤالاتی در مورد جمع چند عدد متوالی مطرح میشود. در اینگونه سؤالات، یکی از اعداد را برابر با \( \Large x \) در نظر بگیرید و بقیه را در مقایسه با آن بنویسید. به عنوان نمونه به موارد زیر توجه کنید:
- سه عدد متوالی: \( \Large x \text { , } x+1 \text { , } x+2 \text { , } \) یا \( \Large x-1 \text { , } x \text { , } x+1 \text { , } \)
- سه عدد زوج (یا فرد) متوالی: \( \Large x \text { , } x+2 \text { , } x+4 \text { , } \) یا \( \Large x-2 \text { , } x \text { , } x+2 \text { , } \)
مثال 8: مجموع سه عدد زوج متوالی برابر با 66 شده است؛ عدد وسط کدام است؟
حل 8:
عدد کوچکتر را \( \Large x \)، عدد وسط را \( \Large x+2 \) و عدد بزرگتر را \( \Large x+4 \) در نظر میگیریم؛ مجموع آنها را بدین صورت برابر 66 مینویسیم:
\( \Large x + (x+2) + (x+4) = 66 \)
\( \Large 3x + 6 = 66 \)
بنابراین این سؤال تبدیل به حل معادله درجه اول شده و طبق مراحل گفته شده بدین صورت محاسبه میشود:
\( \Large 3x + 6 = 66 – 6 = 60 \)
\( \LARGE x = \frac {60}{3} = 20 \)
بنابراین این اعداد 20، 22 و 24 هستند و عدد وسط، 24 خواهد بود.
زنگ آخر کلاس حل معادله درجه اول
با معادلات بسیار زیاد هم در دروس ریاضی و هم در زندگی سر و کار خواهیم داشت و حل معادله درجه اول در واقع اولین گام این راه است. با مطالعه این محتوا، با تعریف معادله و اجزای آن آشنا شدیم و سپس با یک روش مرحله به مرحله توانستیم در چندین مثال متنوع معادلات درجه اول کسری و غیر کسری را حل کنیم.
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاهها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.





خیلی عالی ممنون,?
با سلام وعرض ادب
خوشحالیم که مفید بوده
بله
با سلام وعرض ادب
ممنون
هیچی نفهمیدم
با سلام
کجاش رو نفهمیدید ؟
باسلام خیلی مفید بود
بسیار عالی ممنون متشکر
با سلام وادب
خواهش میکنم عزیز
سلام ببخشید یه سوال داشتم؟
چه موقع در جابه جایی اعداد از طرفین مساوی
برای ساده سازی خود عدد رو قرینه میکنیم و چه موقع توان عدد رو قرینه میکنیم
با سلام وادب
در حل معادله وقتی عدد یا متغیری رو از یه طرف میبریم یه طرف دیگه یا به اصطلاح از روی تساوی می پریم علامت عوض میشه ولی در مورد توان منفی هر وقت بخواهیم مقدار یه عدد تواندار با توان منفی رو بدست بیاریم عدد رومعکوس می کنیم وتوان رو قرینه
سلام
ممنونم ،عالی بود
با سلام دوست عزیز
ممنون از نر شما
سلام وخسته نباشید من ازتون واقعا ممنونم هر چقدر تشکر کنم کمه من دهم انسانی هستم هفتم و هشتم و نهم ما اوفتاد کرونا بخاطر همین نتونسته بودم خوب یاد بگیرم اما با مطالب شما کاملا یاد گرفتم .
با سپاس دوست عزیز خدا رو شکر که در جهت یادگیری فرزاندان این مرز وبوم قدمی برداشته ایم
خیلی خوب وعالی بود
خیلی عالی بود