آموزش ریاضی پایه دوازدهم تجربی
مشتق دوازدهم تجربی 🎶🥀 – به همین سادگی، به همین زیبایی!
در این درسنامه قصد داریم تا به مبحث مشتق دوازدهم تجربی بپردازیم. یکی از نیازهایی که منجر به پیدایش مفهوم مشتق شد، نیاز به ارائهٔ تعریف دقیق از خط مماس بر منحنی بود. در قدیم تعریف خط مماس بر اساس ویژگیهای آن در چند شکل خاص صورت میگرفت. به طور مثال، خطی را بر دایره مماس میگفتند که بر شعاع عمود بوده و فاصلهٔ آن از مرکز دایره برابر با اندازهی شعاع باشد.
اما تعاریفی از این قبیل، تنها برای یک شکل خاص مانند دایره معتبر بود، نه برای یک منحنی با شکل دلخواه. تلاش برای ارائهٔ تعریف خط مماس برای یک منحنی دلخواه، منجر به پیدایش مفهوم مشتق شد. ابتدا تعریف خط مماس برای یک منحنی با شکل دلخواه را با هم میبینیم، سپس به معرفی مفهوم مشتق میپردازیم.
خط مماس بر منحنی ، اولین تعریف از مشتق دوازدهم تجربی
با توجه به توضیحی که در مقدمه دادیم، به دنبال ارائهٔ تعریفی دقیق از خط مماس بر منحنی هستیم. منحنی شکل زیر را در نظر بگیرید.
فرض کنید میخواهیم از نقطهی \(\Large A \) بر منحنی مماس رسم کنیم. نقطهٔ \(\Large P \) را همانند شکل زیر بر روی منحنی مشخص کرده و خط واصل بین \(\Large A \) و \(\Large P \) را رسم میکنیم.
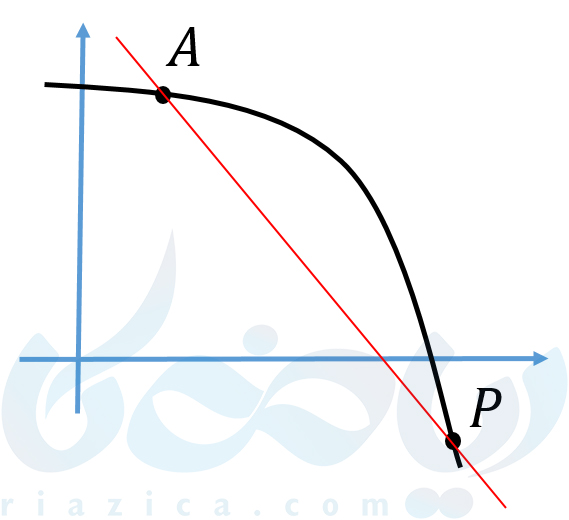
اگر \(\Large P \) را به تدریج به \(\Large A \) نزدیک کنیم، نقاط \(\Large P_1 \) و \(\Large P_2 \) که در شکل زیر مشخص شدهاند، به دست میآیند. خطوط واصل بین \(\Large A \) و این دو نقطهٔ جدید را نیز رسم میکنیم.
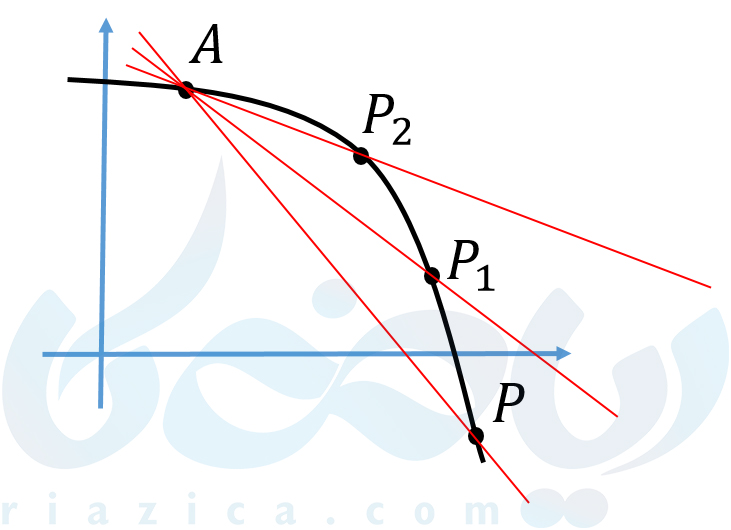
میتوان از شکل بالا حدس زد که اگر \(\Large P \) را بیاندازه به \(\Large A \) نزدیک کنیم، با رسم خط واصل بین آنها، خط مماس به دست میآید. اگر شیب خط مماس را داشته باشیم، از آنجاییکه مختصات نقطهٔ \(\Large A \) که روی خط مماس قرار دارد را نیز داریم، میتوانیم معادلهٔ خط مماس را بنویسیم. از این روست که دانستن مقدار شیب برای ما مهم است.
شیب خط مماس، حالت حدی شیبهای خطوط واصل خواهد بود. برای اینکه این بخش مهم از مبحث مشتق دوازدهم تجربی را بهتر متوجه شوید، مثال زیر را با هم بررسی میکنیم.
شیب خط مماس ، حالت حدی شیب خطوط واصل
مثال 1: نمودار معادلهی \(\Large y=x^2-5x \) را در نظر بگیرید. فرض کنید میخواهیم خط مماس بر نمودار در نقطهی \(\Large A=(3, -6) \) را رسم کنیم.
ابتدا از یک نقطهٔ دلخواه روی نمودار مانند \(\Large P=(6, 6) \)، به نقطهٔ \(\Large A \) خطی رسم میکنیم.
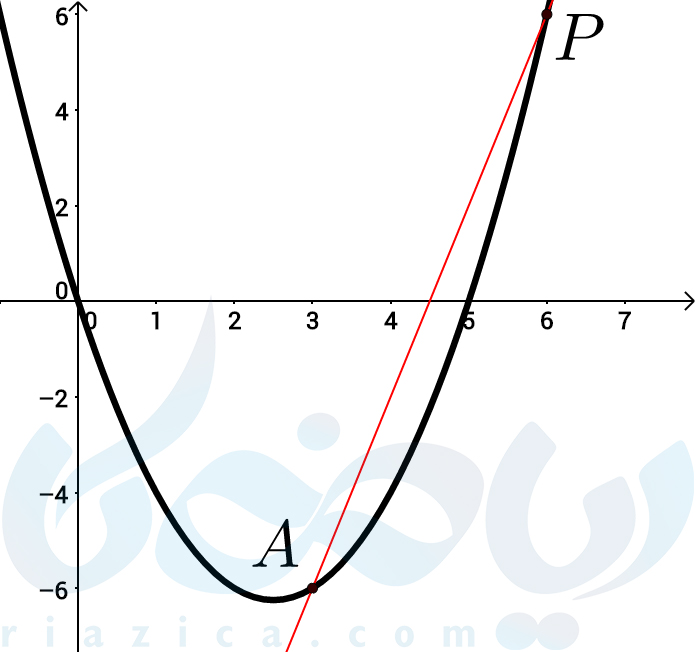
حال سعی میکنیم به تدریج روی نمودار، به نقطهٔ \(\Large A \) نزدیک شویم. بنابراین نقاط \(\Large P_1=(5, 0) \) و \(\Large P_2=(4, -4) \) را نیز روی نمودار مشخص کرده و خط واصل بین نقطهٔ \(\Large A \) و این نقاط را رسم میکنیم.
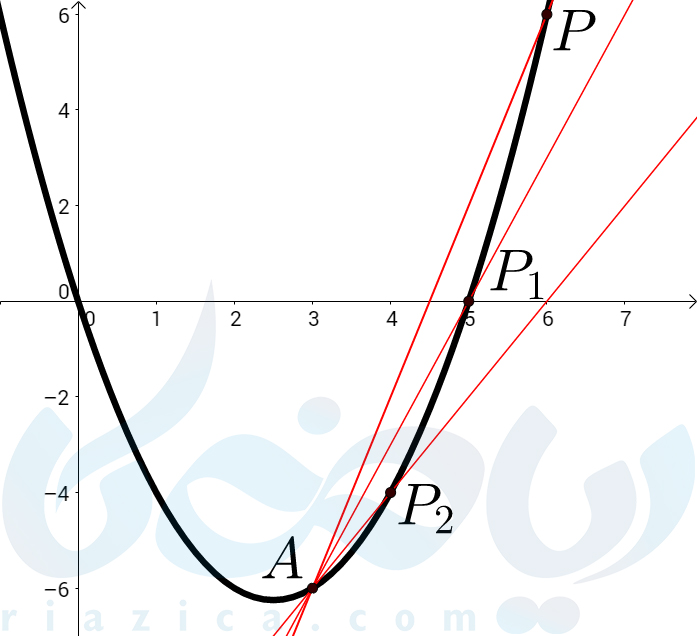
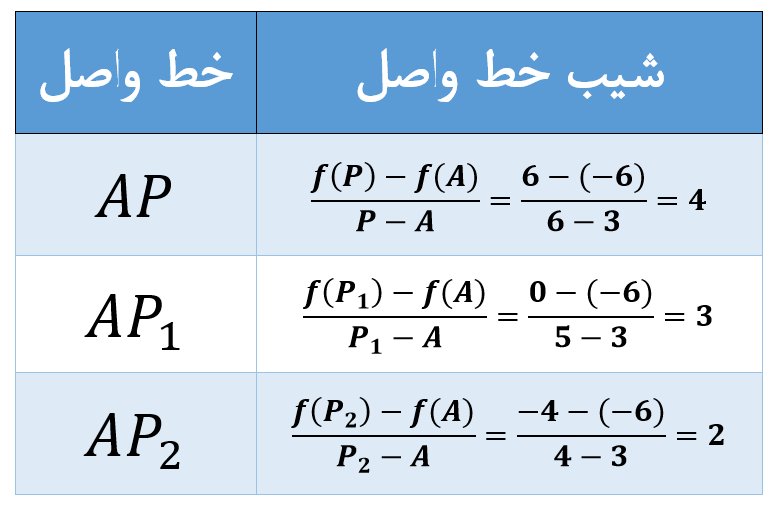
شیب خطوط رسم شده در شکل بالا، در جدول زیر محاسبه شده است. این جدول و جدولهای بعدی میتواند به فهم بهتر شما از مبحث مشتق دوازدهم تجربی کمک زیادی کند.
در صورتی که روند موجود در جدول بالا را ادامه دهیم، مقادیر زیر به دست میآیند:
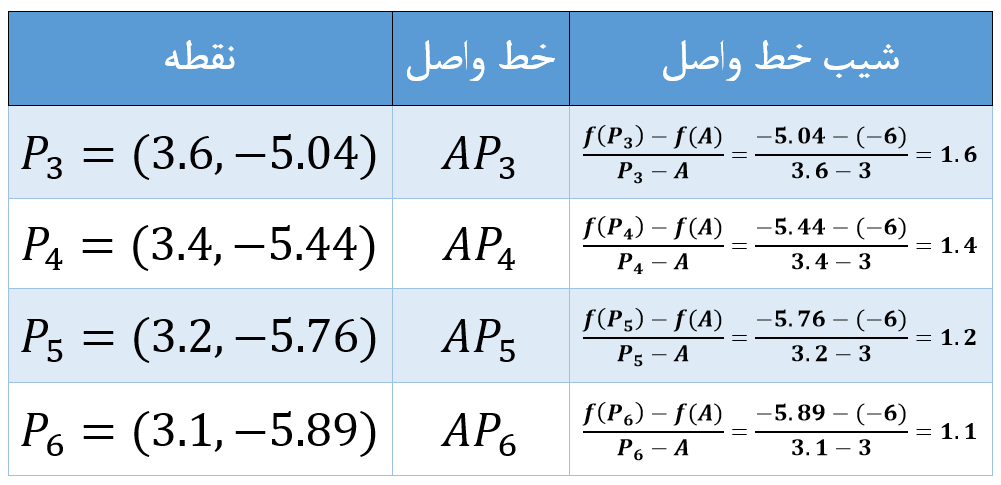
میتوان حدس زد که اگر نقطهٔ \(\Large P \) را به \(\Large A \) نزدیک کنیم، شیب خط واصل که همان شیب خط مماس خواهدبود، به عدد \(\Large 1 \) میل خواهدکرد.
نکتهای که باید در این مثال از مشتق دوازدهم تجربی دقت کنید این است که، در این مثال اگر نقطهٔ \(\Large P \) را از سمت چپ به \(\Large A \) نزدیک میکردیم، باز هم شیب خطوط واصل به عدد \(\Large 1 \) میل میکرد. در شکل زیر، از سمت چپ به نقطهٔ \(\Large A \) نزدیک شده و خطوط واصل را رسم کردیم.
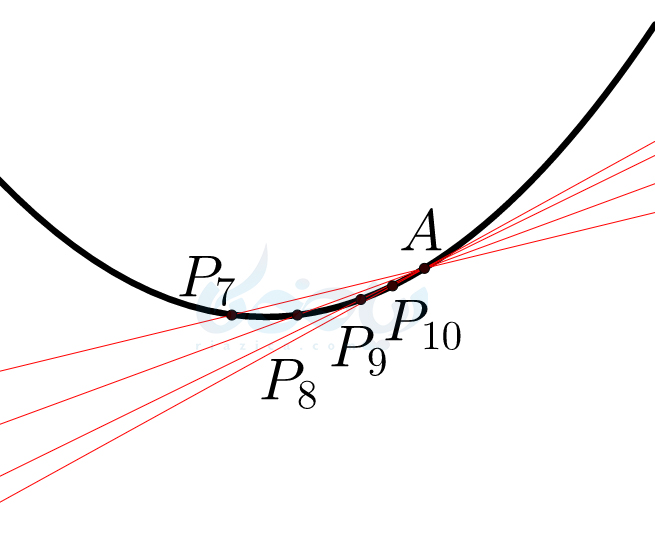
در جدول زیر میتوانید شیب خطوط واصل برای نقاطی که روی نمودار در سمت چپ نقطهی \(\Large A \) قرار دارند را نیز ببینید.
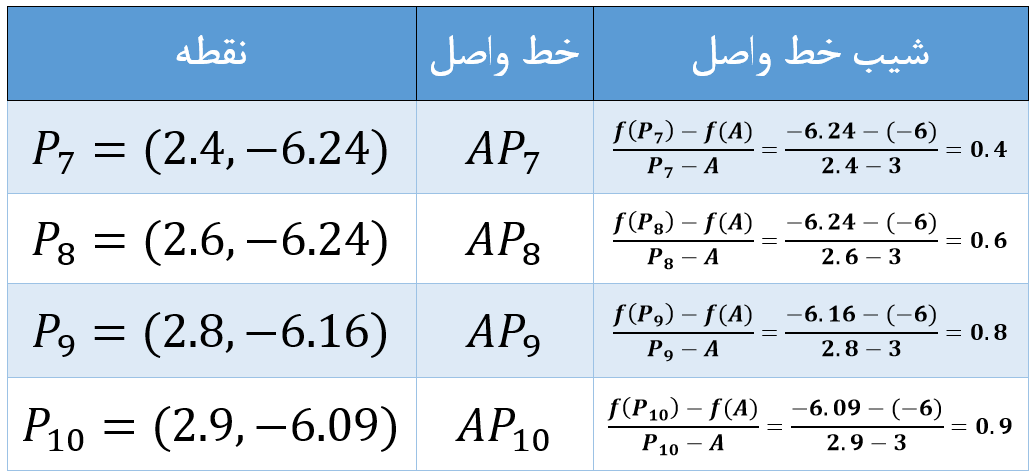
همانطور که در جدول بالا پیداست، باز هم شیب خطوط واصل به عدد \(\Large 1 \) میل میکند. بنابراین، همان طور که دیدید، برای پیدا کردن شیب خط مماس بر منحنی در نقطهٔ \(\Large A \) باید از دو طرف به نقطهٔ \(\Large A \) نزدیک شده و حد شیب خطوط واصل را به دست آوریم.
دلیل علاقه و کنجکاوی ما برای دانستن شیب خط مماس از این جهت است که با دانستن آن میتوان معادلهٔ خط مماس بر منحنی را به دست آورد. در ادامهٔ مبحث مشتق دوازدهم تجربی، روش محاسبهٔ دقیق شیب خط مماس را بررسی میکنیم.
مشتق و رابطهی آن با شیب خط مماس
همانطور که دیدیم، شیب خط مماس بر منحنی در یک نقطه برابر است با مقدار حدی شیب خطوط واصل بین آن نقطه و نقاط دیگر منحنی. برای محاسبهٔ مقدار شیب تابع \(\Large f(x) \) در نقطهی \(\Large a \) دو روش داریم:
- روش اول: نقطهی \(\Large (a+h, f(a+h)) \) را که روی منحنی قرار دارد در نظر بگیرید. برای آنکه این نقطه را بی اندازه به نقطهٔ \(\Large a \) نزدیک کنیم، مقدار \(\Large h \) را به سمت صفر میل میدهیم. شیب خط واصل بین نقطهی \(\Large (a+h, f(a+h)) \) و \(\Large (a, f(a)) \) که همان شیب خط مماس است، برابر است با \(\Large \frac{\Delta y}{\Delta x} \) که مقدار آن برابر میشود با:
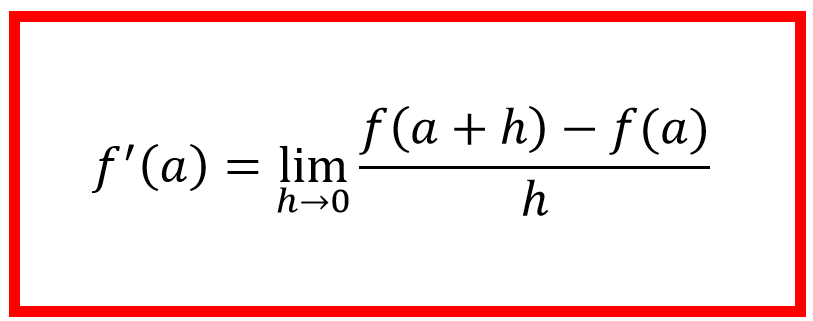
- روش دوم: همان طور که در شکلهای قسمت قبل دیدیم، برای پیدا کردن شیب خط مماس بر منحنی در یک نقطه کافی است از دو طرف به آن نقطه نزدیک شده و حد شیب خطوط واصل را به دست آوریم. اما برای نزدیک شدن به یک نقطه، روشی معادل روش اول نیز وجود دارد. نقطهای روی نمودار با مختصات متغیر \(\Large (x, f(x)) \) را در نظر میگیریم. برای اینکه آن را بی اندازه به نقطهی \(\Large (a, f(a)) \) نزدیک کنیم، مقدار \(\Large x \) را به \(\Large a \) میل میدهیم. شیب خط واصل بین نقطهی \(\Large (a, f(a)) \) و \(\Large (x, f(x)) \) که همان شیب خط مماس است، برابر است با \(\Large \frac{\Delta y}{\Delta x} \) که مقدار آن برابر میشود با:
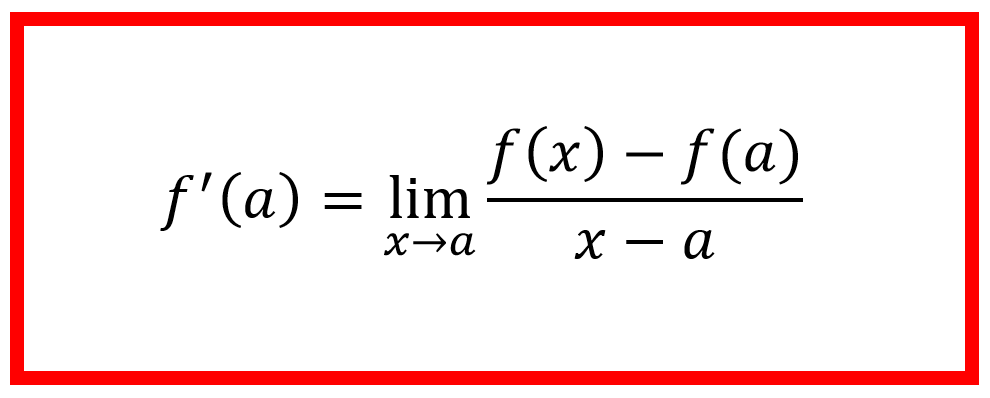
در شکل زیر، با استفاده از نمودار (الف) میتوان مطابق روش اول و با استفاده از نمودار (ب) میتوان مطابق روش دوم شیب خط مماس در نقطهٔ \(\Large a \) را به دست آورد.
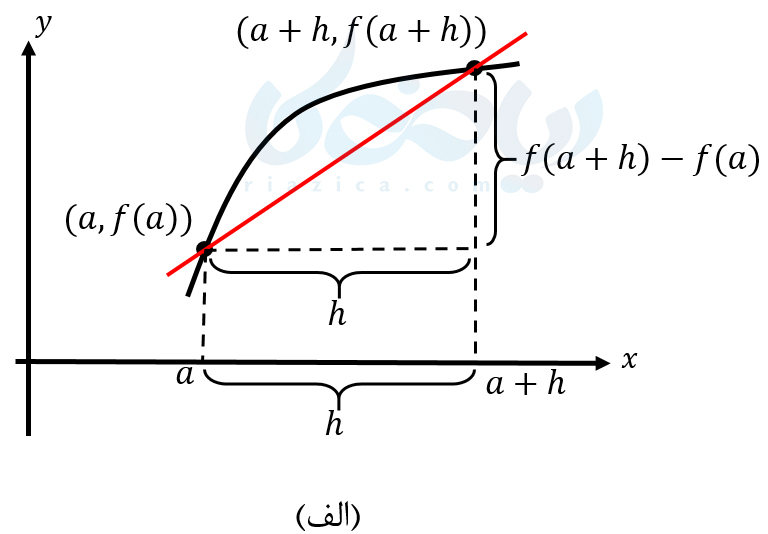
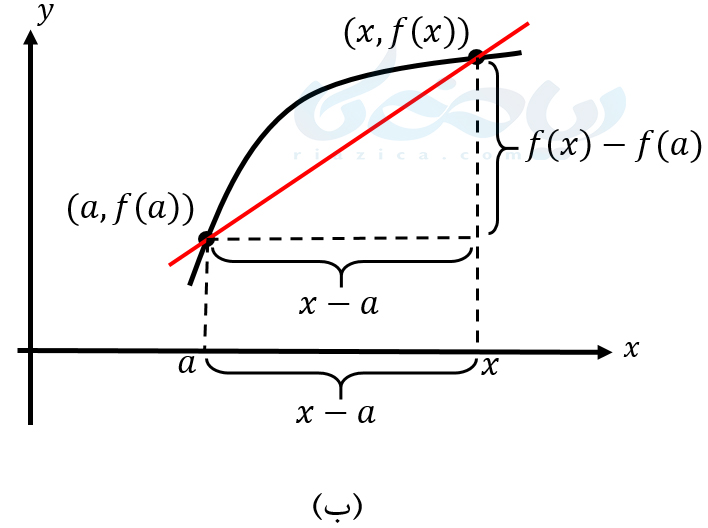
تفاوتی ندارد که از کدام یک از دو روش بالا استفاده کنیم، در هر روش در صورتی که حد معرفی شده موجود باشد، حاصل آن را که شیب خط مماس بر منحنی است، مشتق تابع \(\Large f(x) \) در نقطهٔ \(\Large a \) مینامیم و آن را با نماد \(\Large f'(a) \) نمایش میهیم. در ادامه باهم مثالهای بیشتری را از مشتق دوازدهم تجربی بررسی خواهیم کرد.
مثالهای از محاسبهٔ مشتق دوازدهم تجربی
مثال 2: شیب خط مماس بر منحنی \(\Large f(x)=x^2-5x \) را در نقطهی \(\Large x=6 \)، با استفاده از هر دو روش معرفی شده به دست آورید.
حل: شیب خط مماس بر منحنی یا همان مشتق تابع \(\Large f(x) \) در نقطهی \(\Large x=6 \) با استفاده از دو روش معرفی شده، به صورت زیر به دست میآید:
- روش اول:
\(\LARGE f'(6)=\lim\limits_{h\to 0} \frac{f(6+h)-f(6)}{h}\)
\(\LARGE =\lim\limits_{h\to 0} \frac{(6+h)^2-5(6+h)-(6^2-30)}{h}\)
\(\LARGE =\lim\limits_{h\to 0} \frac{h^2+7h+6-6}{h}\)
\(\LARGE =\lim\limits_{h\to 0} \frac{h^2+7h}{h}\)
\(\LARGE =\lim\limits_{h\to 0} \frac{h(h+7)}{h}\)
\(\LARGE =\lim\limits_{h\to 0} h+7=7\)
- روش دوم:
\(\LARGE f'(6)=\lim\limits_{x\to 6} \frac{f(x)-f(6)}{x-6}\)
\(\LARGE =\lim\limits_{x\to 6} \frac{x^2-5x-(6^2-30)}{x-6}\)
\(\LARGE =\lim\limits_{x\to 6} \frac{x^2-5x-6}{x-6}\)
\(\LARGE =\lim\limits_{x\to 6} \frac{(x+1)(x-6)}{x-6}\)
\(\LARGE =\lim\limits_{x\to 6} x+1=7\)
مثال 3: اگر \(\Large f(x)=2x^3-3 \) باشد، \(\Large f'(-3) \) را با استفاده از هر دو روش معرفی شده به دست آوردید.
حل:
- روش اول:
\(\LARGE f'(-3)=\lim\limits_{h\to 0} \frac{f(-3+h)-f(-3)}{h}\)
\(\LARGE =\lim\limits_{h\to 0} \frac{2(-3+h)^3-3-(-54-3)}{h}\)
\(\LARGE =\lim\limits_{h\to 0} \frac{2h^3-18h^2+54h-54+54}{h}\)
\(\LARGE =\lim\limits_{h\to 0} \frac{h(2h^2-18h+54)}{h}\)
\(\LARGE =\lim\limits_{h\to 0} 2h^2-18h+54\)
\(\LARGE =54\)
- روش دوم:
\(\LARGE f'(-3)=\lim\limits_{x\to -3} \frac{f(x)-f(-3)}{x-(-3)}\)
\(\LARGE =\lim\limits_{x\to -3} \frac{2x^3-3-(-54-3)}{x+3}\)
\(\LARGE =\lim\limits_{x\to -3} \frac{2x^3+54}{x+3}\)
\(\LARGE =\lim\limits_{x\to -3} \frac{2(x^3+27)}{x+3}\)
\(\LARGE =\lim\limits_{x\to -3} \frac{2(x+3)(x^2-3x+9)}{x+3}\)
\(\LARGE =\lim\limits_{x\to -3} 2(x^2-3x+9)\)
\(\LARGE =54\)
مثال 4: اگر \(\Large f(x)=\sqrt[3]{x} \) باشد، \(\Large f'(1) \) را با استفاده از هر دو روش معرفی شده به دست آوردید.
حل:
- روش اول:
\(\LARGE f'(1)=\lim\limits_{h\to 0} \frac{f(1+h)-f(1)}{h}\)
\(\LARGE =\lim\limits_{h\to 0} \frac{\sqrt[3]{1+h}-\sqrt[3]{1}}{h}=\)
\(\Large \lim\limits_{h\to 0} \frac{(\sqrt[3]{1+h}-\sqrt[3]{1})(\sqrt[3]{(1+h)^2}+\sqrt[3]{1+h}+1)}{h(\sqrt[3]{(1+h)^2}+\sqrt[3]{1+h}+1)}\)
\(\LARGE =\lim\limits_{h\to 0} \frac{(1+h)-1}{h(\sqrt[3]{(1+h)^2}+\sqrt[3]{1+h}+1)}\)
\(\LARGE =\lim\limits_{h\to 0} \frac{h}{h(\sqrt[3]{(1+h)^2}+\sqrt[3]{1+h}+1)}\)
\(\LARGE =\lim\limits_{h\to 0} \frac{1}{\sqrt[3]{(1+h)^2}+\sqrt[3]{1+h}+1}\)
\(\LARGE =\frac{1}{3}\)
- روش دوم:
\(\LARGE f'(1)=\lim\limits_{x\to 1} \frac{f(x)-f(1)}{x-1}\)
\(\LARGE =\lim\limits_{x\to 1} \frac{\sqrt[3]{x}-\sqrt[3]{1}}{x-1}\)
\(\LARGE =\lim\limits_{x\to 1} \frac{(\sqrt[3]{x}-\sqrt[3]{1})(\sqrt[3]{x^2}+\sqrt[3]{x}+\sqrt[3]{1})}{(x-1)(\sqrt[3]{x^2}+\sqrt[3]{x}+\sqrt[3]{1})}\)
\(\LARGE =\lim\limits_{x\to 1} \frac{x-1}{(x-1)(\sqrt[3]{x^2}+\sqrt[3]{x}+\sqrt[3]{1})}\)
\(\LARGE =\lim\limits_{x\to 1} \frac{1}{\sqrt[3]{x^2}+\sqrt[3]{x}+\sqrt[3]{1}}\)
\(\LARGE =\frac{1}{3}\)
در ادامه توصیه میشه پست مشتق پذیری دوازدهم تجربی را مطالعه کنید.
زنگ آخر کلاس مفهوم مشتق و مشتق دوازدهم تجربی
در این درسنامه به بررسی مبحث مشتق دوازدهم تجربی پرداختیم. همان طور که گفتیم، لزوم ارائهٔ تعریف دقیق از خط مماس بر یک منحنی دلخواه، منجر به تعریف مشتق شد. شیب خط مماس بر منحنی در یک نقطه برابر است با مشتق تابع در آن نقطه. دو روش برای محاسبهی مشتق معرفی کردیم که هر دو نتیجهی یکسانی داشتند.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث مشتق دوازدهم تجربی دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





اشتراکها: مشتق توابع مثلثاتی 🔮📐 - تمام آنچه میخواهید!! - ریاضیکا | ریاضی آسان است
سپاس عالی بود
ممنون از نظر شما