زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعی‌ها!

می‌خواهید وارد قلعه چندضلعی‌ها شوید؟ مشکلی نیست، اما ابتدا باید از نگهبان‌هایی به نام زاویه های خارجی عبور کنید. این نگهبان‌ها دور تا دور قلعه قرار گرفته‌اند و محل نگهبانی آن‌ها، گوشه‌های چندضلعی است. با عبور از این مرحله، به پشت دیوار (زاویه های داخلی) خواهید رسید؛ برای ماجراجویی این درس آماده باشید…!

این درس‌نامه از مجموعه آموزش ریاضی پایه هشتم ، ابتدا با مقدمه‌ای برای یادآوری مفهوم چندضلعی محدب و مقعر شروع شده و سپس با زاویه های خارجی در چندضلعی‌ها آشنا خواهید شد. با یادگیری نکاتی از جمله زاویه خارجی چندضلعی منتظم و رابطه زاویه های داخلی و خارجی و سپس حل چند مثال مهم، از این موضوع با قدرت عبور خواهید کرد.

---

---

مقدمه: چندضلعی محدب و مقعر

در ریاضیات پایه هفتم با چندضلعی محدب و مقعر آشنا شدیم. از آن‌جا که در این درس برای تعریف زاویه های خارجی به مفهوم چندضلعی محدب نیاز داریم، جهت یادآوری تعاریف زیر را مرور می‌کنیم:

چندضلعی محدب (کوژ)

به چندضلعی که همه زاویه‌های آن از °180 کوچکتر باشد، چندضلعی محدب (کوژ) گفته می‌شود.

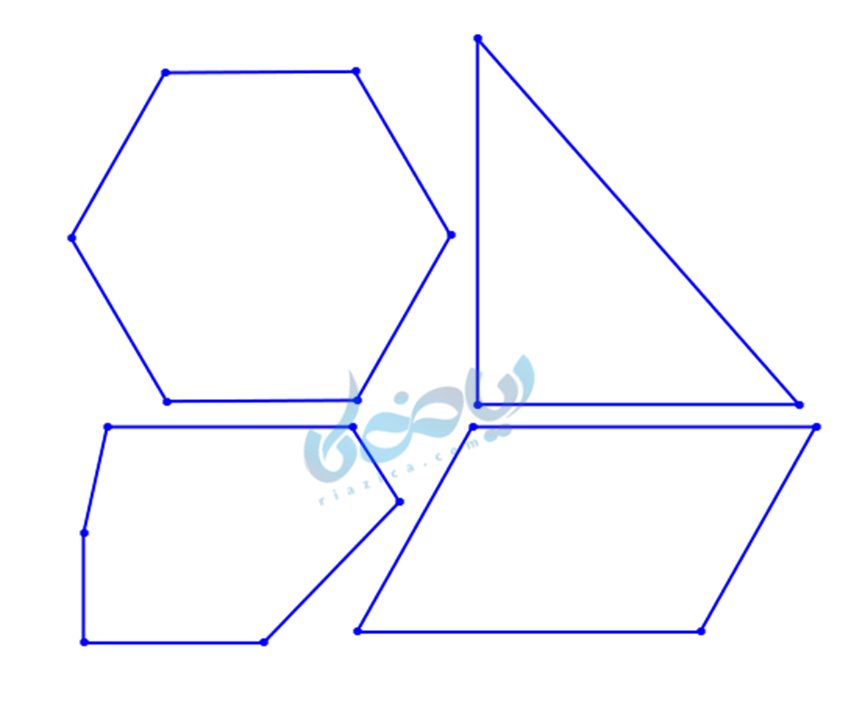
چندضلعی‌های نشان داده شده همگی محدب هستند، چون هیچ زاویه داخلی بزرگتر از °180 ندارند.

چندضلعی مقعر (کاو)

به چندضلعی که حداقل یک زاویه بزرگتر از °180 داشته باشد، چندضلعی مقعر (کاو) گفته می‌شود.

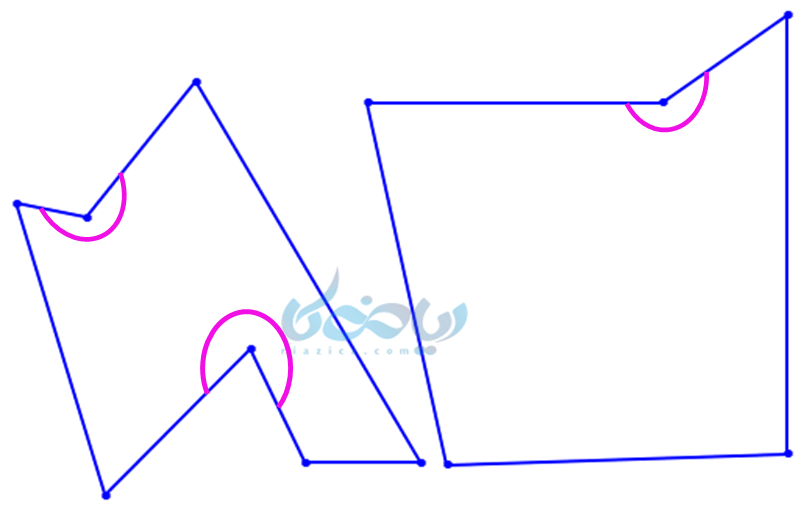
چندضلعی سمت چپ دو زاویه و چندضلعی سمت راست یک زاویه بزرگتر از بزرگتر از °180 دارند و هر دو، چندضلعی مقعر هستند.

نکته: توجه کنید که در تعریف چندضلعی محدب و مقعر، ملاک زاویه های داخلی است نه زاویه های خارجی .

راه تشخیص چندضلعی محدب و مقعر

در یک چندضلعی، دو نقطه دلخواه در نظر می‌گیریم و آن‌ها را با یک خط راست به هم وصل می‌کنیم. اگر این خط درون چندضلعی قرار گرفت، چندضلعی محدب و اگر قسمتی از آن بیرون چندضلعی قرار گرفت، چندضلعی مقعر است.

مثال 1: محدب یا مقعر بودن چندضلعی‌های زیر را تعیین کنید.

حل 1:

برای تشخیص نوع چندضلعی، در هر چندضلعی بررسی می‌کنیم که آیا اگر هر دو نقطه‌ای در چندضلعی در نظر بگیریم و با خط راست به هم وصل کنیم، آن خط کاملاً درون چندضلعی قرار می‌گیرد یا خیر.

الف)

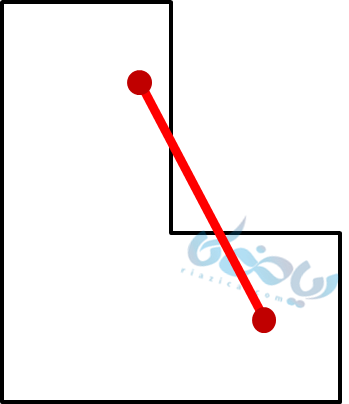
همان‌طور که می‌بینیم در این چندضلعی دو نقطه در نظر گرفته‌ایم که قسمتی از خط راستی که آن دو را به هم وصل می‌کند، خارج از چندضلعی قرار گرفته است. پس این چندضلعی مقعر خواهد بود.

ب)

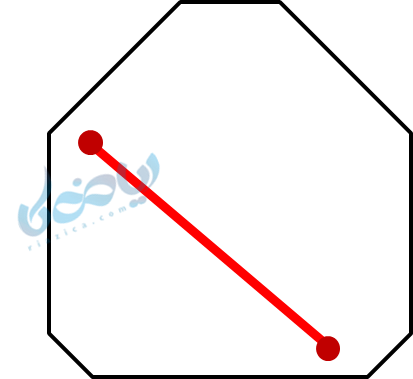
آیا می‌توانید دو نقطه در این چندضلعی پیدا کنید که خط راست بین آن‌ها کاملاً درون چندضلعی نباشد؟ خیر! پس این چندضلعی محدب است.

تعریف زاویه های خارجی

زاویه‌ای که در هر رأس یک چند ضلعی محدب، بین یک ضلع و امتداد ضلع دیگر تشکیل می‌شود، زاویه خارجی آن رأس نامیده می‌شود.

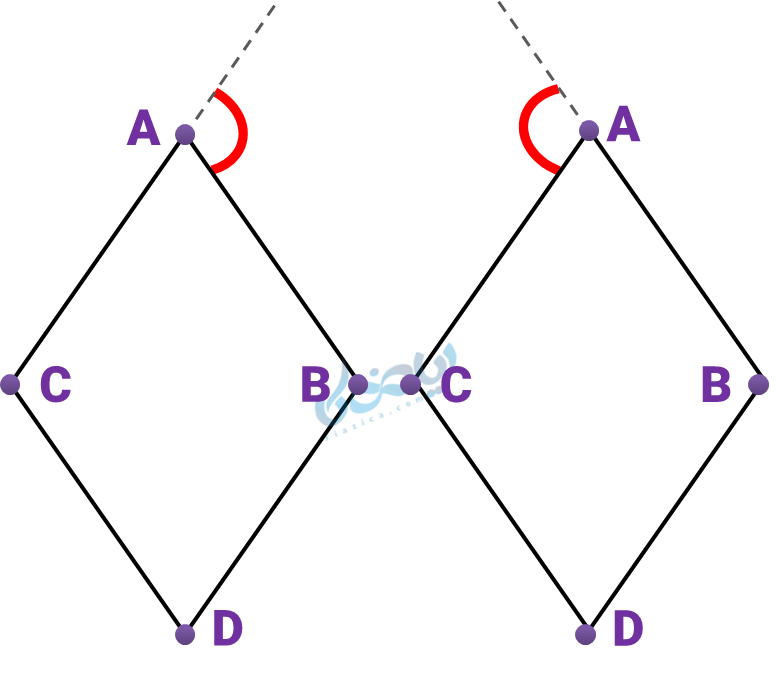
به عنوان نمونه در لوزی نشان داده شده می‌خواهیم برای رأس \( \Large A \) زاویه خارجی رسم کنیم. می‌توانیم یکی از این دو را به عنوان زاویه خارجی در نظر بگیریم:

• زاویه بین ضلع \( \Large \overline {AB} \) و امتداد ضلع \( \Large \overline {AC} \) (شکل سمت چپ)
• زاویه بین ضلع \( \Large \overline {AC} \) و امتداد ضلع \( \Large \overline {AB} \) (شکل سمت راست)

توجه کنید که اندازه زاویه خارجی در این دو حالت برابرند و هیچ فرقی ندارد کدام ضلع را امتداد دهیم. (چرا؟) چون هر دو با زاویه داخلی، زاویه °180 می‌سازند.

تفاوت زاویه های خارجی با زاویه های داخلی

برای این که بهتر تفاوت زاویه های خارجی و زاویه های داخلی را متوجه شوید، به چندضلعی زیر توجه کنید:

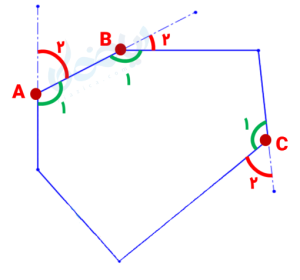
در چندضلعی محدب بالا در سه رأس به عنوان نمونه، زاویه های خارجی به رنگ قرمز و زاویه های داخلی به رنگ سبز نشان داده شده است.

نکته: در هر رأس چندضلعی، زاویه خارجی و زاویه داخلی مکمل یکدیگرند. به عنوان مثال در چندضلعی بالا در رأس \( A \):

\( \Large \hat {A_1} + \hat {A_2} = 180° \)

مثال 2: در هر چندضلعی زیر، زاویه خارجی را در رأس \( A \) مشخص کرده و اندازه آن را بدست آورید.

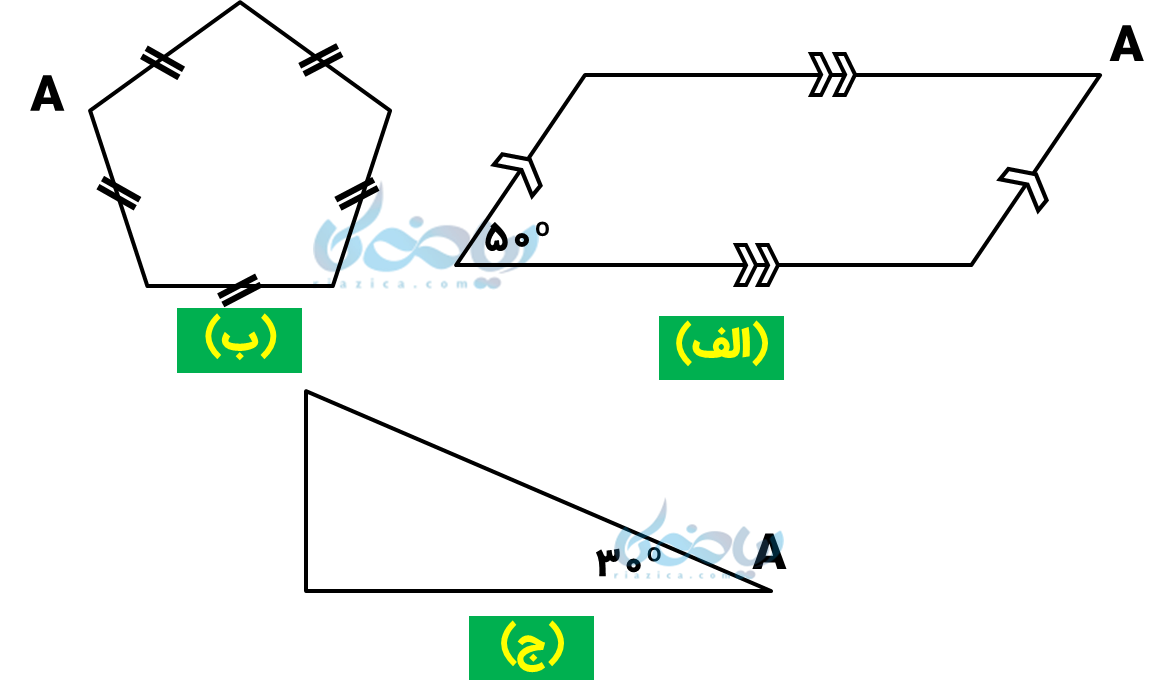
حل 2:

برای حل این سؤال از این نکته استفاده می‌کنیم که زاویه های خارجی و داخلی در یک رأس مکمل یکدیگرند.

الف)

در درس چهارضلعی‌ها آموختیم که در متوازی‌الاضلاع زاویه‌های روبرو با هم برابرند؛ یعنی:

\( \Large \hat {A_1} = 50° \)

حال از نکته گفته شده استفاده می‌کنیم:

\( \Large \hat {A_1} + \hat {A_2} = 180° \)

\( \Large → 50° + \hat {A_2} = 180° \)

\( \Large → \hat {A_2} = 180° – 50° = 130° \)

ب)

شکل داده شده یک پنج‌ضلعی منتظم است. در درس زاویه‌های داخلی رابطه محاسبه زاویه داخلی چندضلعی منتظم را آموختیم؛ در این رابطه به جای \( \Large n \)، عدد 5 قرار می‌دهیم:

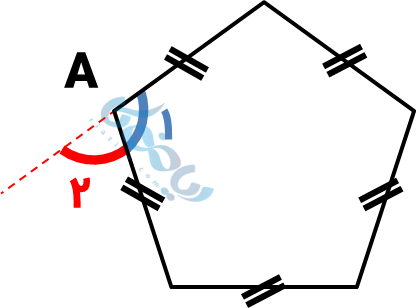
\( \Large \hat {A_1} = \frac {(n-2) × 180°}{n}  \)

\( \Large \hat {A_1} = \frac {(5-2) × 180°}{5}  \)

\( \Large \hat {A_1} = \frac {3 × 180°}{5}  \)

\( \Large → \hat {A_1} = 108° \)

حال از نکته گفته شده استفاده می‌کنیم:

\( \Large \hat {A_1} + \hat {A_2} = 180° \)

\( \Large → 108° + \hat {A_2} = 180° \)

\( \Large → \hat {A_2} = 180° – 108° = 72° \)

ج)

با توجه به معلوم بودن زاویه داخلی، با استفاده از نکته گفته شده زاویه خارجی را بدست می‌آوریم:

حال از نکته گفته شده استفاده می‌کنیم:

\( \Large \hat {A_1} + \hat {A_2} = 180° \)

\( \Large → 30° + \hat {A_2} = 180° \)

\( \Large → \hat {A_2} = 180° – 30° = 150° \)

---

---

داستان مثلث و زاویه خارجی

اندازه هر زاویه خارجی مثلث برابر است با مجموع دو زاویه داخلی غیرمجاور آن. به عنوان نمونه در مثلث زیر، داریم:

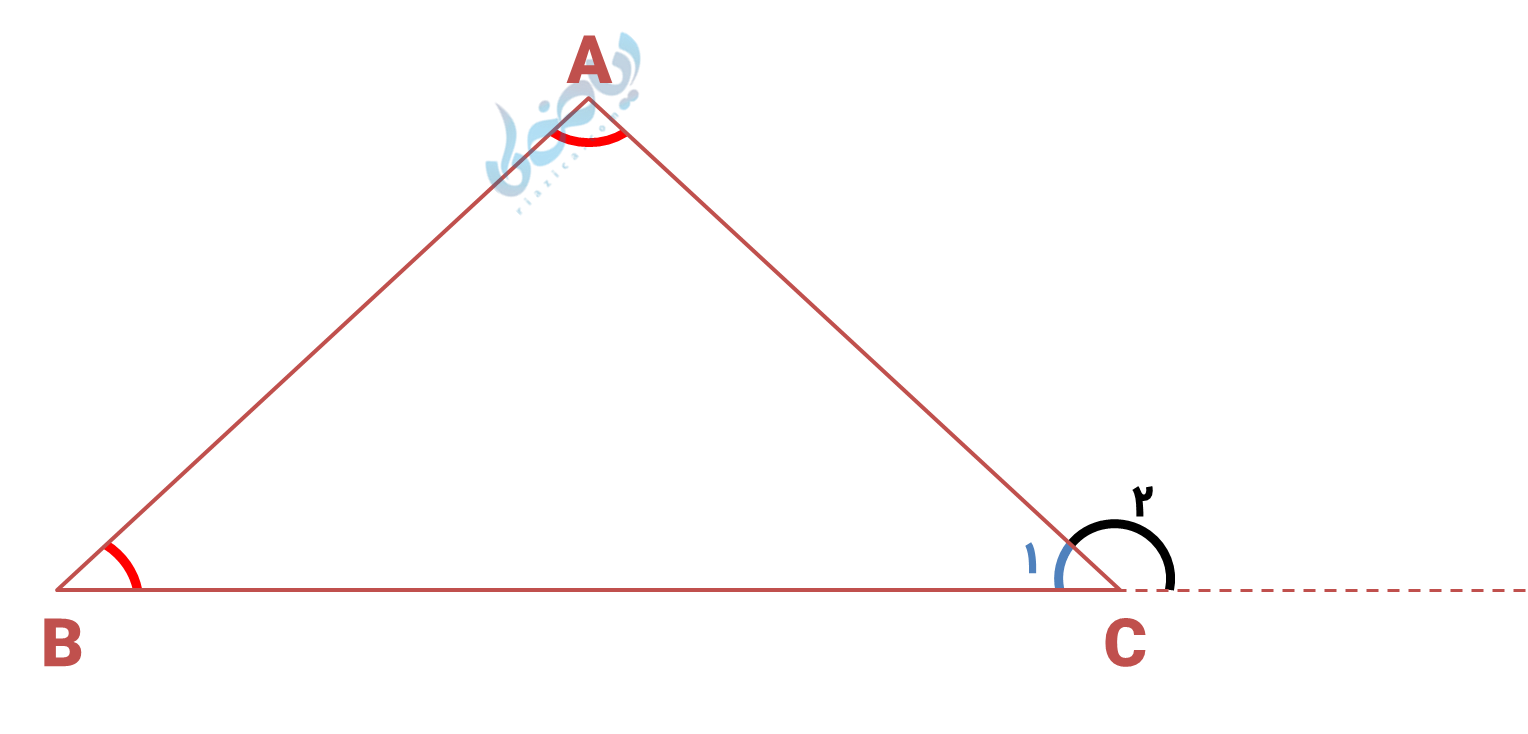
\( \Large \hat {C_2} = \hat A + \hat B \)

اثبات

• الف: در درس زاویه های داخلی یاد گرفتیم که مجموع زوایای داخلی یک مثلث برابر با °180 است.
• ب: در نکته بالا دیدیم که زاویه های خارجی و داخلی هر رأس مکمل یکدیگرند.

بیایید این دو جمله را به زبان ریاضی بنویسیم تا بهتر نتیجه‌گیری کنیم:

\( \Large \hat A + \hat B + \hat {C_1} = 180° \) (الف)

\( \Large \hat {C_1} + \hat {C_2} = 180° \) (ب)

با مقایسه دو رابطه (الف) و (ب) می‌توان نتیجه گرفت که:

\( \Large \hat {C_2} = \hat A + \hat B \)

نکته: این قضیه در مورد چندضلعی‌های دیگر برقرار نیست. به عنوان مثال در چهارضلعی زیر که یک مربع است، زاویه خارجی یک رأس برابر با مجموع سه زاویه داخلی غیرمجاور نیست.

در این مربع می‌بینید که زاویه خارجی \( \Large \hat {B_2} \) برابر با °90 است؛ در حالی که مجموع سه زاویه داخلی دیگر برابر با °270 است.

اندازه زاویه های خارجی در چندضلعی‌ها

مجموع زاویه های خارجی یک چندضلعی

مجموع زاویه‌های خارجی هر چندضلعی برابر با °360 است.

اثبات

• الف: در درس زاویه های داخلی دیدیم که مجموع زوایای داخلی یک \( \Large n \)– ضلعی برابر است با \( \Large (n-2) × 180° \).
• ب: زاویه های خارجی و داخلی هر رأس مکمل یکدیگرند؛ پس مجموع زوایای داخلی و خارجی یک \( \Large n \)– ضلعی برابر است با  \( \Large n × 180° \).

به دو جمله (الف) و (ب) توجه کنید؛ برای این که مجموع زاویه های خارجی یک \( \Large n \)– ضلعی را بدست آوریم کافی است مجموع زوایای داخلی (الف) را از مجموع زوایای داخلی و خارجی (ب) کم کنیم:

\( \Large n × 180° – (n-2) × 180° \)

\( \Large = n × 180° – n × 180° + 2 × 180° \)

\( \Large = 2 × 180° = 360° \)

مثال 3: جدول زیر در مورد زاویه های خارجی و داخلی است. آن را کامل کنید.

حل 3:

در درس زاویه های داخلی یاد گرفتیم که مجموع زوایای داخلی یک \( \Large n \)– ضلعی برابر است با:

\( \Large (n-2) × 180° \)

همچنین از نکته بالا با روش محاسبه مجموع زاویه های داخلی و خارجی و همچنین مجموع زاویه های خارجی آشنا شدیم،؛ بنابراین در جدول فوق، تنها کافی است از فرمول‌های گفته شده استفاده کنیم و در هر مرحله به جای  \( \Large n \) تعداد اضلاع را جای‌گذاری کنیم.

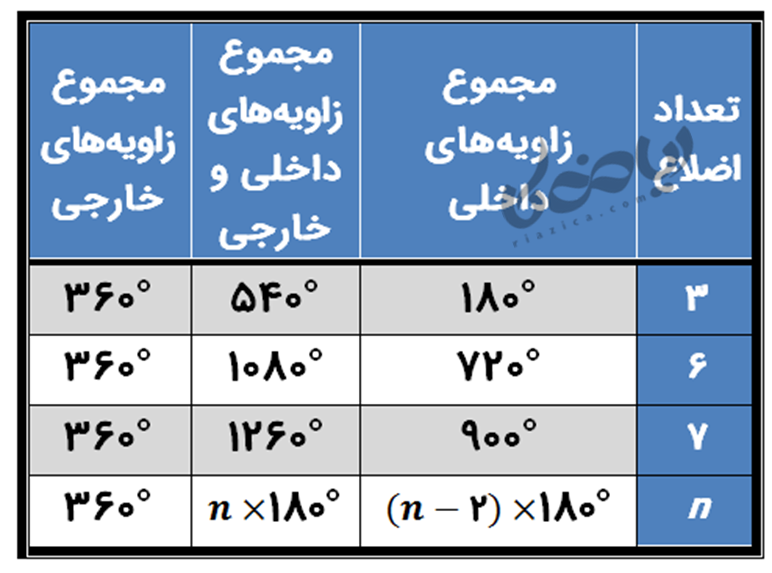
برای نمونه جاهای خالی برای 6 ضلعی محاسبه می‌شود:

\( \Large (6-2) × 180° \) (مجموع زاویه‌ های داخلی)

\( \Large = 4 × 180° = 720° \)

\( \Large n × 180° \) (مجموع زاویه‌ های داخلی و خارجی)

\( \Large = 6 × 180° = 1080° \)

\( \Large 360° \) (مجموع زاویه‌ های خارجی)

به همین ترتیب برای سایر چندضلعی‌ها محاسبات را انجام داده و در جدول زیر نوشته‌ایم:

اندازه زاویه خارجی یک چندضلعی منتظم

اندازه هر یک از زاویه‌های خارجی یک \( \Large n \)– ضلعی منتظم برابر است با:

\( \LARGE \frac {360°}{n} \)

که در این رابطه \( \Large n \) تعداد اضلاع را نشان می‌دهد.

اثبات

الف: می‌دانیم مجموع زاویه‌های خارجی هر چندضلعی برابر با °360 است.

ب: در چندضلعی منتظم، زاویه های داخلی با هم برابرند، پس زاویه های خارجی نیز برابرند.

بنابراین چون \( \Large n \)– ضلعی منتظم دارای \( \Large n \) زاویه خارجی است، پس اندازه هر زاویه برابر است با: \( \Large \frac {360°}{n} \)

مثال 4: مجموع زاویه های داخی یک چندضلعی منتظم برابر با °1260 است. هر زاویه خارجی این چندضلعی چند درجه است؟

حل 4:

در درس زاویه های داخلی رابطه مجموع زوایای داخلی چندضلعی را یاد گرفتیم. با مساوی قرار دادن این رابطه با °1260تعداد اضلاع بدست خواهد آمد:

\( \Large (n-2) × 180° = 1260° \)

\( \Large → (n-2) = \frac {1260}{180} = 7 \)

\( \Large → n= 7 + 2 = 11\)

حالا برای محاسبه اندازه هر زاویه خارجی 9 ضلعی منتظم از رابطه زیر استفاده می‌کنیم:

\( \LARGE \frac {360°}{n} → \frac {360°}{9} = 40° \)

ویدیو از زاویه های خارجی چند ضلعی ها

در این ویدیو در مورد زوایه های داخلی وخارجی چند ضلعی ها مطالب گفته شده ونمونه سوالی از این مبحث حل شده است

زنگ آخر کلاس زاویه های خارجی

در این سفر هیجان‌انگیز، با هم از گوشه‌های قلعه چندضلعی‌ها و محل نگهبانی زاویه های خارجی رد شدیم و از اسرار این قلعه یعنی چندضلعی محدب و مقعر، اندازه زاویه خارجی در چندضلعی منتظم و مجموع زوایای خارجی در چندضلعی‌ها آگاه شدیم. حال با خیال راحت از این قلعه خارج می‌شویم و برای همیشه خاطره و تجربیات آن را در ذهن خواهیم داشت.

در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاه‌ها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.

---

---

به خوندن ادامه بده!

زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعی‌ها!تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!