آموزش ریاضی پایه هشتم
زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
اردیبهشت
دایره، یکی از پرکاربردترین شکل‌های موجود در زندگی ماست که در ریاضیات و هندسه مدام با مسائل آن سر و کار داریم. آموزش زاویه های دایره : زاویه محاطی و زاویه مرکزی که از سری آموزش ریاضی پایه هشتم است.
در این آموزش چه خواهیم گفت
در این آموزش خواهیم دید که خطوط و نقطه‌هایی که داخل دایره وجود دارند، می‌توانند دایره را به چند بخش تقسیم کنند. همچنین این خطوط و نقطه ها زاویه‌هایی به وجود می‌آورند که با یادگیری ویژگی‌های منحصر بفرد آن‌ها، بخش مهمی از مسائل هندسه در دایره برای ما حل خواهد شد. در این درس‌نامه، کمان، زاویه های دایره شامل زاویه مرکزی و زاویه محاطی و ویژگی‌های هر یک از آن‌ها با جزئیات آموزش داده میشود. در ادامه نیز با حل چند مثال، از این به بعد با خیال راحت از این موضوع در هندسه استفاده می‌کنیم.
کمان دایره
تعریف کمان
قسمتی از محیط دایره است که بین 2 نقطه قرار می‌گیرد؛ مانند دو نقطه A و B روی محیط دایره زیر که کمان AB را ایجاد کرده است.
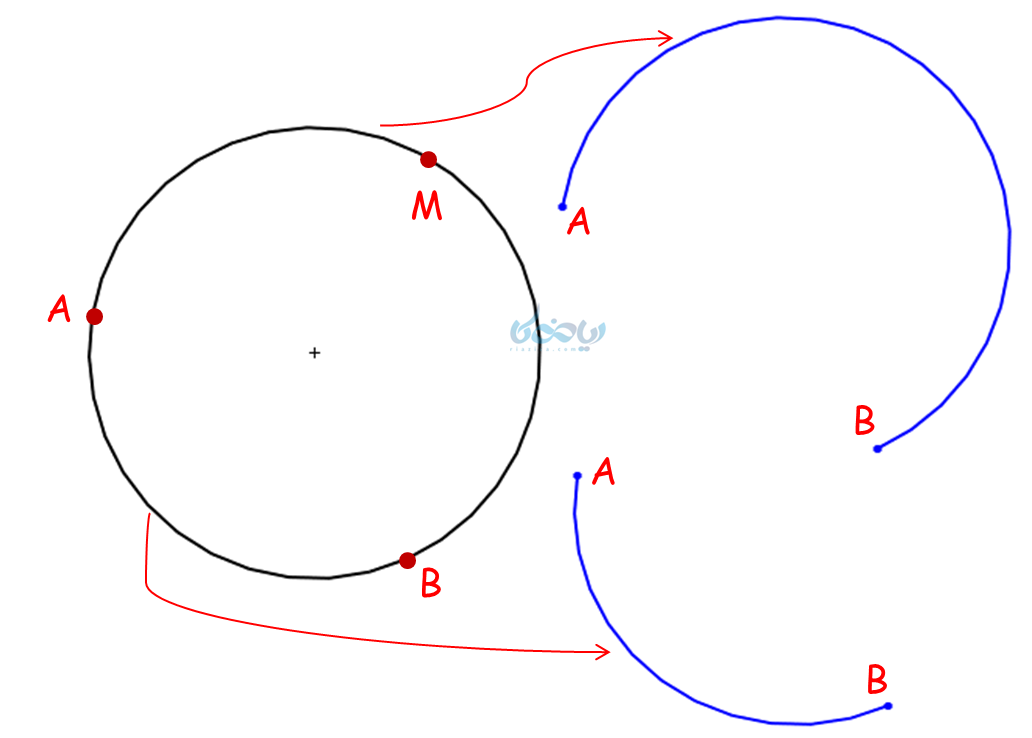
نکته 1: هر دو نقطه بر روی دایره، در واقع آن را به دو کمان تقسیم می‌کنید: کمان کوچکتر و بزرگتر. به عنوان مثال، دو کمان آبی رنگ در شکل بالا.
نکته 2: کمان با دو حرف (مانند وتر) یا سه حرف نام‌گذاری میشود؛ مثلاً در شکل قبل، کمان AB بزرگتر را می‌توان بصورت AMB نیز نشان داد.
نکته 3: دایره، کمانی است که نقطه ابتدا و انتهای آن یکسان است. در شکل بالا، فرض کنید یک کمان از نقطه M شروع شود و به همان نقطه ختم گردد.
نحوه بیان بزرگی یک کمان
بزرگی یک کمان را می‌توان به دو صورت بیان نمود:
- اندازه کمان
- طول کمان
اندازه کمان
اندازه یک کمان بر حسب زاویه بیان میشود. اندازه کمان AB در شکل زیر برابر با °120 است.
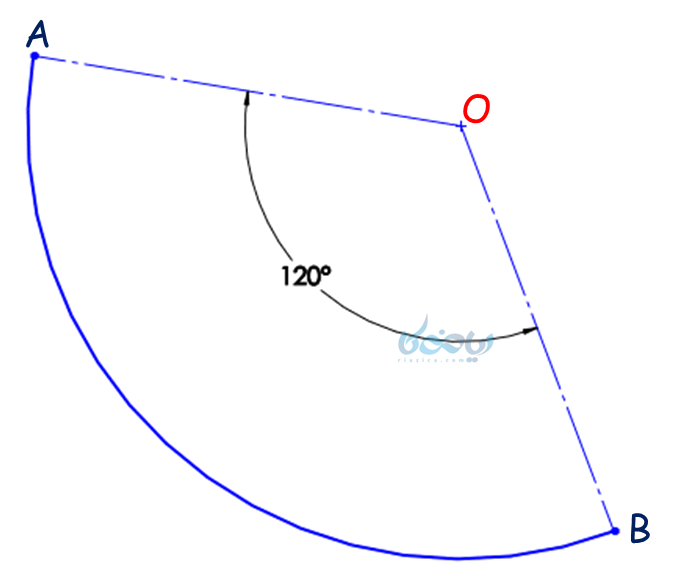
همان‌طور که می‌دانیم، یک دایره (همچون نکته 3 بخش قبل) برابر با °360 است؛ بنابراین در صورت داشتن اندازه یک کمان، با نوشتن یک تناسب ساده می‌توان تعیین کرد که این کمان چه کسری از دایره است.
همچنین برای بدست آوردن اندازه یک کمان که می‌دانیم دایره را به چند قسمت مساوی تقسیم کرده است، کافی است °360 را به آن تعداد تقسیم کنیم.
مثال 1: کمان نشان داده شده در شکل زیر چه کسری از دایره است؟
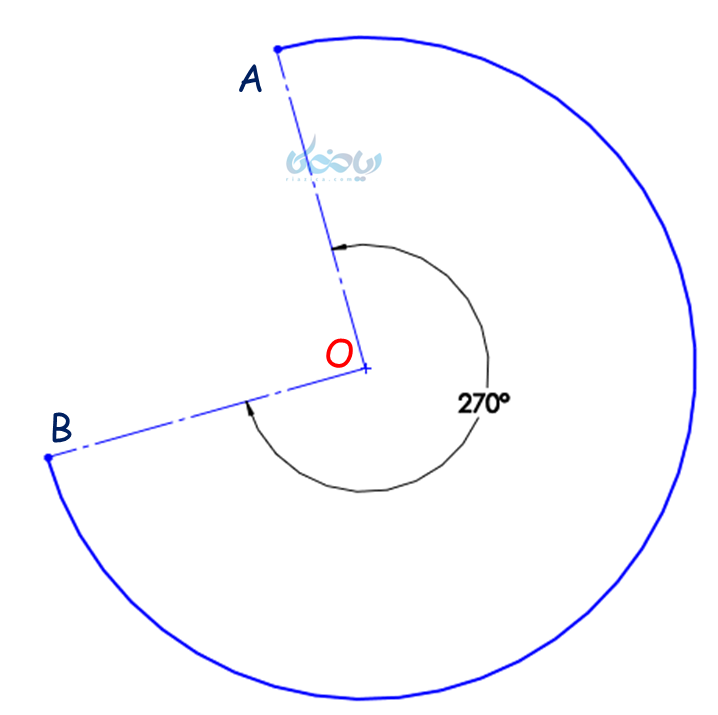
حل 1:
اندازه کمان AB برابر با °270 است؛ بنابراین برای پاسخ به این سؤال این اندازه را با °360 تقسیم می‌کنیم:
\(\Large\ \frac {\stackrel \frown {AB}}{360}=\frac {3}{4} \)
یعنی کمان AB، سه ربع دایره است.
طول کمان
طول کمان، اندازه بخشی از محیط دایره است که کمان در آن بخش قرار دارد. اگر دایره به تعدادی مساوی کمان تقسیم شده باشد، مشابه روشی که در اندازه کمان بکار بردیم، طول یک کمان را از تقسیم محیط دایره به تعداد بخش‌های مساوی بدست می‌آوریم. به عبارت دیگر:
مثال 2: دایره‌ای به شعاع 10 سانتی‌متر، با رسم 9 شعاع از مبدأ، به 9 قسمت مساوی تقسیم شده است. اندازه و طول همه کمان‌های ایجاد شده توسط شعاع‌ها را بدست آورید.
حل 2:
در صورت سؤال گفته شده است که با رسم شعاع؛ یعنی منظور بدین شکل بوده است:
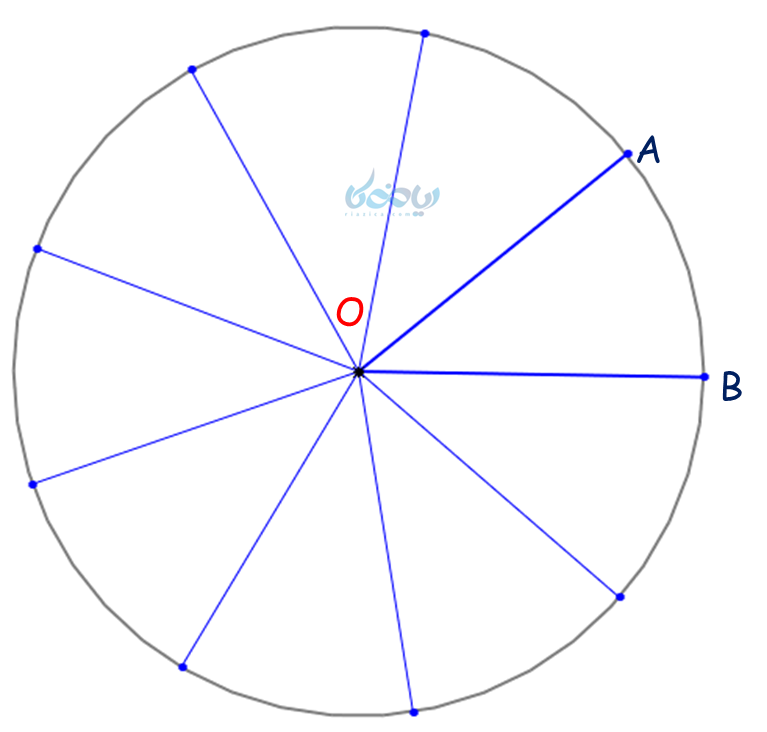
چون گفته شده به 9 قسمت مساوی، بنابراین محاسبه اندازه و طول تنها یکی از کمان‌ها کافی است. اندازه کمان AB برابر است با:
\(\Large\ \stackrel \frown{AB}= \frac {360}{9}= 40° \)
در (ریاضیات پایه پنجم، فصل ششم) یاد گرفتیم که محیط دایره از فرمول \(\Large\ P= 2πr \) بدست می‌آید که \( \Large r \) همان شعاع دایره است، پس طول کمان \( \Large \stackrel \frown{AB} \) برابر است با:
\(\Large\ \stackrel \frown{AB}= \frac {2πr}{9}=\frac {20π}{9} \)
زاویه های دایره
انواع وضعیت‌های قرار گرفتن زاویه های دایره
بطور کلی می‌توان وضعیت‌های زیر را برای زاویه های دایره در نظر گرفت:
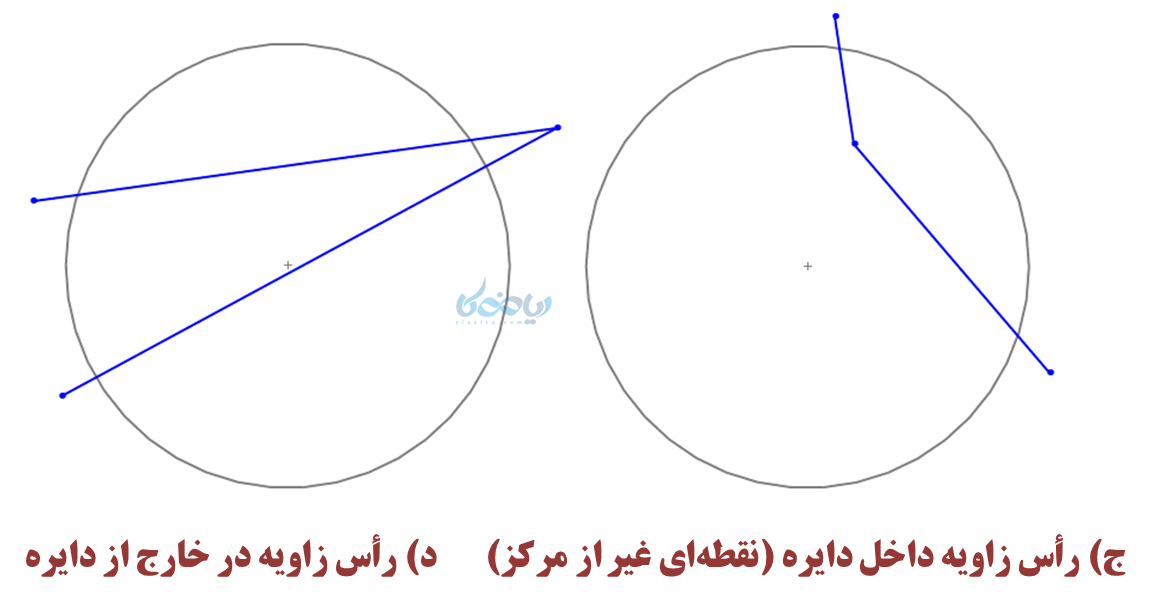
حالت‌های (الف) و (ب)، زوایای خاصی از دایره به نام زاویه مرکزی و محاطی هستند که ویژگی‌های آن‌ها در ادامه مورد بحث قرار خواهد گرفت.
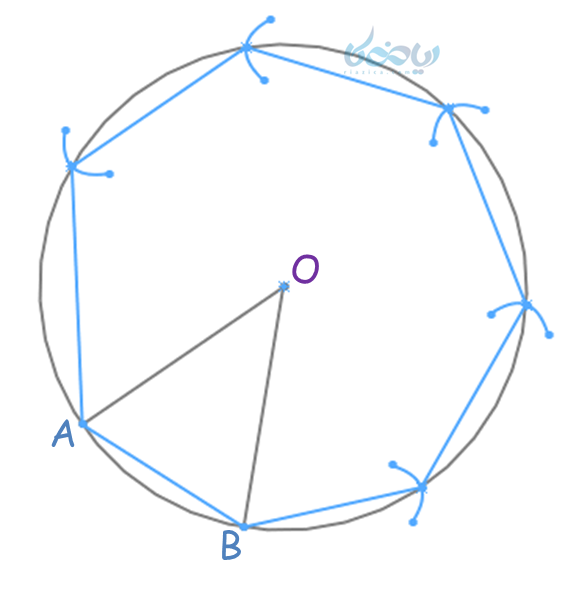
زاویه مرکزی
تعریف زاویه مرکزی
زاویه‌ای است که رأس آن، مرکز دایره و دو ضلع آن، شعاع‌های دایره میباشد. زاویه O در دایره زیر یک زاویه مرکزی دایره است.
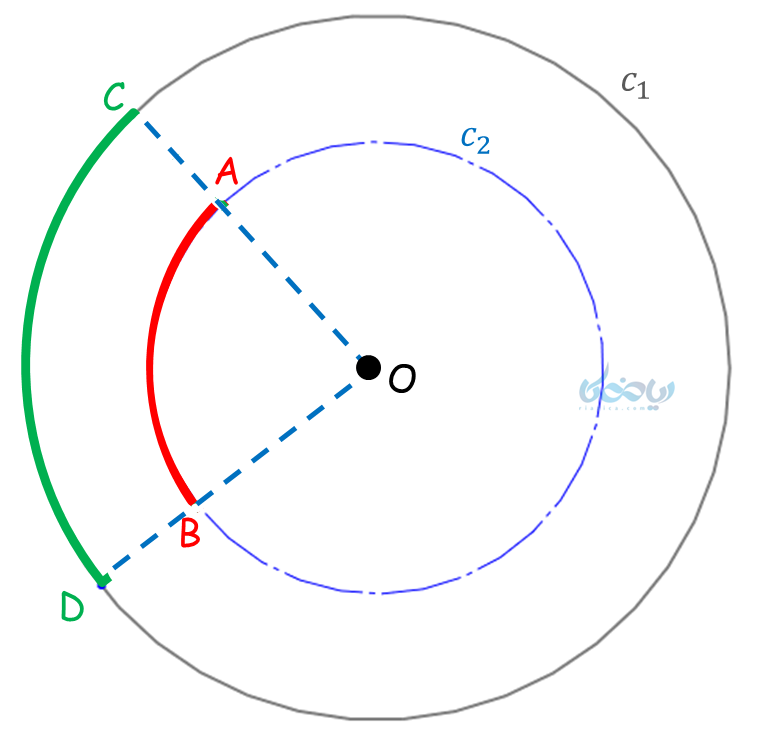
اندازه زاویه مرکزی
اندازه زاویه مرکزی برابر است با اندازه کمان روبروی آن. در شکل بالا اندازه کمان‌های \(\Large\ \stackrel \frown{AB} \) و \(\Large\ \stackrel \frown{CD} \) هر دو برابر با اندازه زاویه \( \Large \hat O \) میباشد.
تذکر: طول کمان‌های \(\Large\ \stackrel \frown{AB} \) و \(\Large\ \stackrel \frown{CD} \) برابر نیست (مطابق بخش قبل)؛ بلکه به شعاع دایره‌های \( \Large c_1 \) و \( \Large c_2 \) بستگی دارد.
نکات مربوط به زاویه مرکزی
از خصوصیت زاویه مرکزی که در بالا بیان شد، می‌توان نکات زیر را نتیجه‌گیری نمود:
- اگر در یک دایره دو کمان با هم برابر باشد، وترهای نظیر آن‌ها نیز برابر است.
- اگر دایره به تعدادی کمان مساوی تقسیم شود، وترهای نظیر آن‌ها تشکیل چندضلعی منتظم می‌دهند.
اثبات نکته اول (زاویه مرکزی):
فرض کنید در دایره زیر \(\Large\ \stackrel \frown{AB}= \stackrel \frown{CD} \) باشد. زوایای \( \hat O_1 \) و \( \hat O_2 \)، زاویه های دایره از نوع مرکزی هستند، پس با کمان‌های روبروی خود مساویند و این یعنی \( \Large \hat O_1= \hat O_2 \).
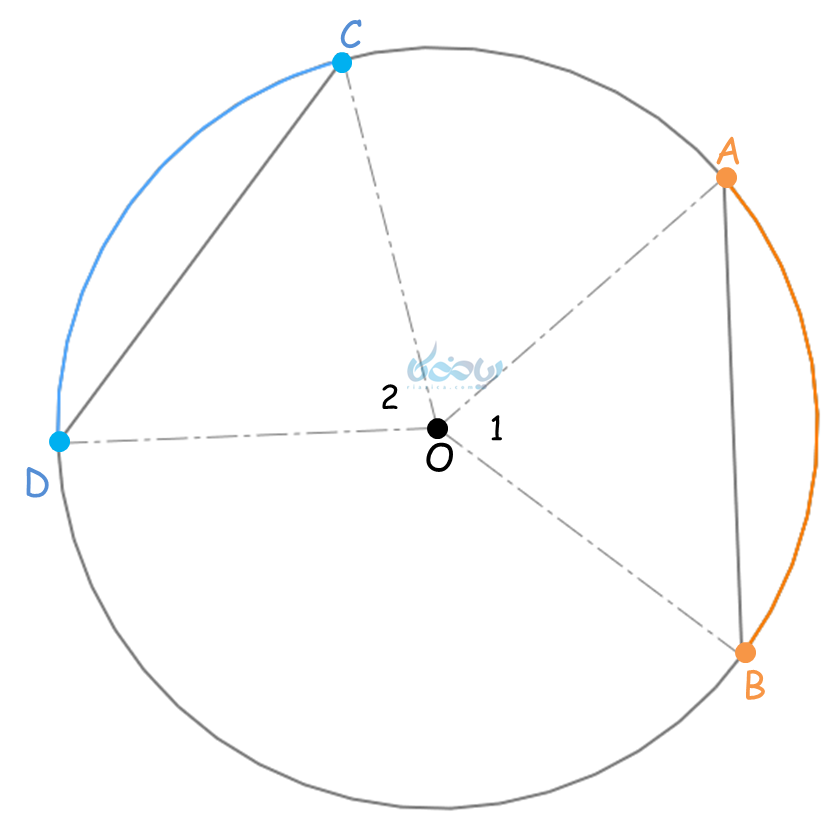
مثلث‌های \( \Large OAB \) و \( \Large OCD \)به حالت برابری دو ضلع و زاویه بین (ض ز ض) همنهشت هستند (یادآوری: مثلث های هم نهشت)، چون:
\( \Large \hat O_1 = \hat O_2 \)
(شعاع‌های دایره)\( \Large \overline {OA} = \overline {OC} \)
(شعاع‌های دایره)\( \Large \overline {OB} = \overline {OD} \)
با توجه به هم‌نهشتی این دو مثلث، وترهای \( \Large \overline {AB} \) و \( \Large \overline {CD} \)با بکدیگر برابرند.
رسم چندضلعی منتظم به کمک خاصیت زاویه مرکزی
برای تقسیم دایره به \( n \) کمان موازی (یا رسم \( n \) -ضلعی منتظم)، ابتدا اندازه محیط دایره را به \( n \) تقسیم می‌کنیم، بنابراین اندازه هر کمان برابر با \(\Large \frac {360}{n} \) میباشد. نقاله را از مرکز دایره منطبق بر شعاع OA گذاشته و به اندازه (\(\Large \frac {360}{n} \)) زاویه‌ای رسم می‌کنیم.
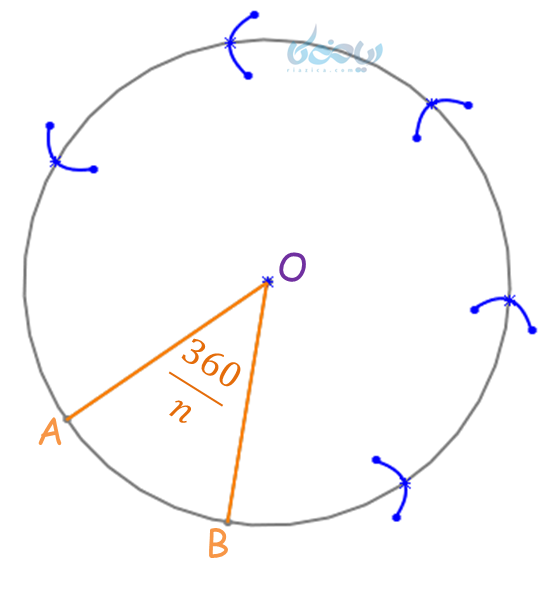
سپس به کمک پرگار از نقطه B، به اندازه وتر AB کمان رسم می‌کنیم تا محیط دایره را در نقاطی مشابه کمان‌های آبی رنگ در دایره بالا قطع کند. همچنین با رسم وترهای متناظر این کمان‌ها، \( n \) -ضلعی منتظم مانند شکل زیر بدست می‌آید.
زاویه محاطی
تعریف زاویه محاطی
زاویه‌ای است که رأس آن روی محیط دایره و دو ضلع آن، وترهایی از دایره میباشد. مانند زاویه T در دایره زیر.
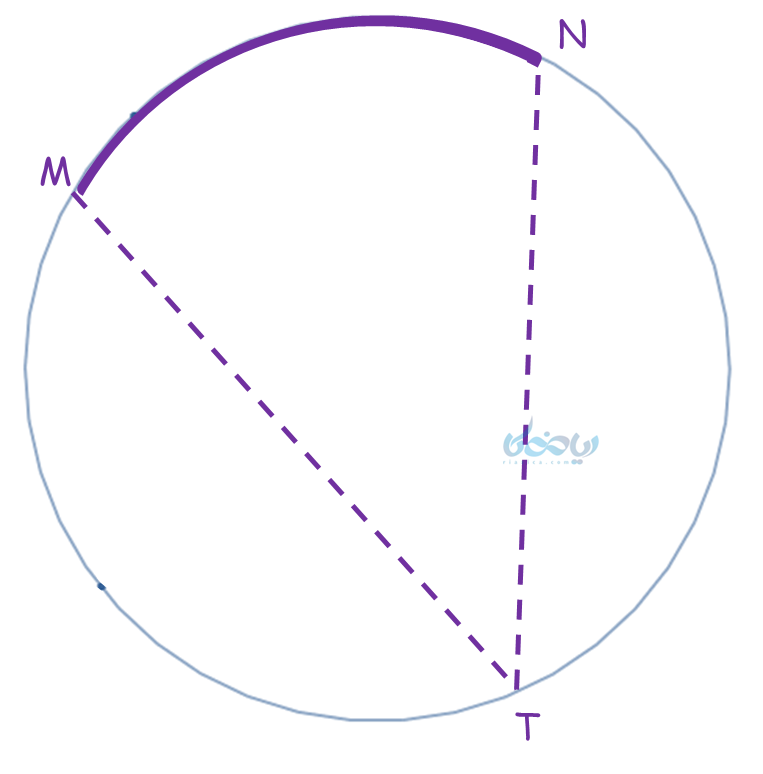
اندازه زاویه محاطی
اندازه زاویه محاطی برابر است با نصف اندازه کمان روبروی آن.
نکات مربوط به زاویه محاطی
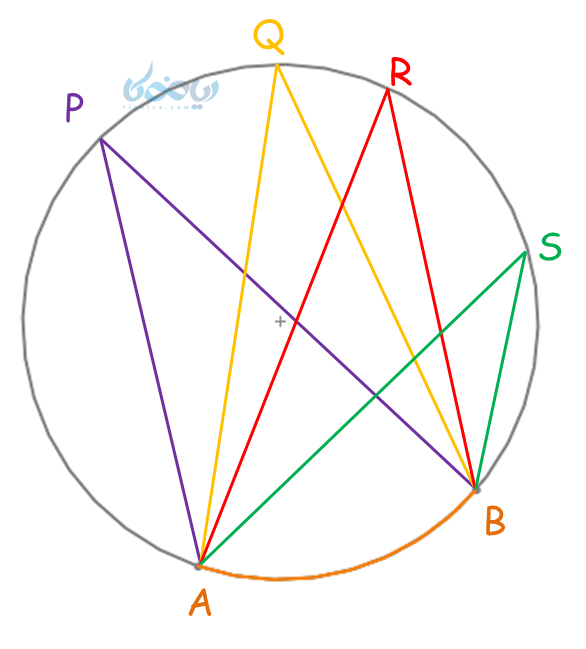
از خصوصیت ذکر شده برای زاویه محاطی، نکات زیر برداشت میشود:
- همه زاویه‌های محاطی روبروی یک کمان با هم برابرند. (مانند زوایای P، Q، R و S)
- روبروی یک کمان می‌توان بی‌نهایت زاویه محاطی رسم کرد.
- زاویه محاطی روبروی قطر دایره برابر با °90 است.
- اگر همه رأس‌های یک چهارضلعی روی محیط دایره قرار داشته باشند، زوایای روبروی هم مکمل یکدیگرند.
اثبات نکته چهارم (زاویه محاطی):
چهارضلعی قرار گرفته در دایره زیر را در نظر بگیرید. مشاهده میشود که کمان‌های \(\Large\ \stackrel \frown{BCD} \)و \(\Large\ \stackrel \frown{BAD} \) یک دایره کامل را می‌سازند، پس مجموع این کمان‌ها برابر با °360 میباشد.
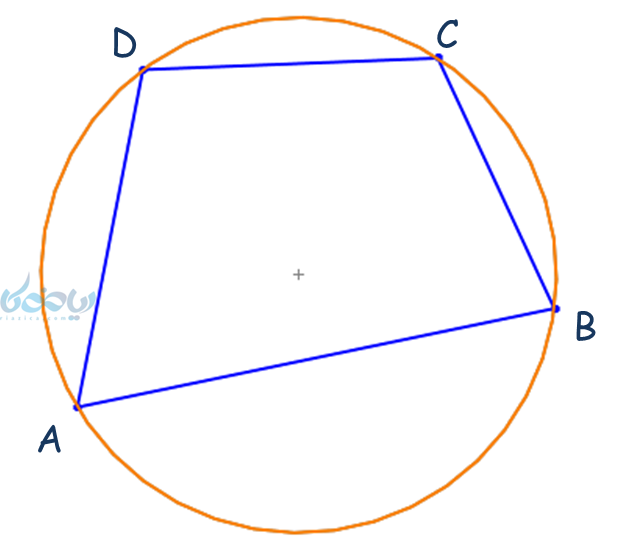
\(\Large\ \stackrel \frown{BCD}+ \stackrel \frown{BAD}=360° \)
از طرفی زاویه‌های محاطی دایره، نصف کمان روبروی خود هستند:
\(\Large\ \hat A=\frac{\stackrel \frown{BCD}}{2} \)
\(\Large\ \hat C=\frac{\stackrel \frown{BAD}}{2} \)
با قرار دادن اندازه کمان روبروی زاویه‌های محاطی در رابطه اول خواهیم داشت:
\(\Large\ 2 \hat A+ 2 \hat C=360° \)
\(\Large\ 2 (\hat A+ \hat C)=360° \)
\(\Large\ \hat A+ \hat C=180° \)
پس زوایای A و C مکمل یکدیگرند. این روند را می‌توان برای زوایای B و D نیز انجام داد.
مثال 3: در شکل زیر، اندازه زاویه A را بدست آورید.
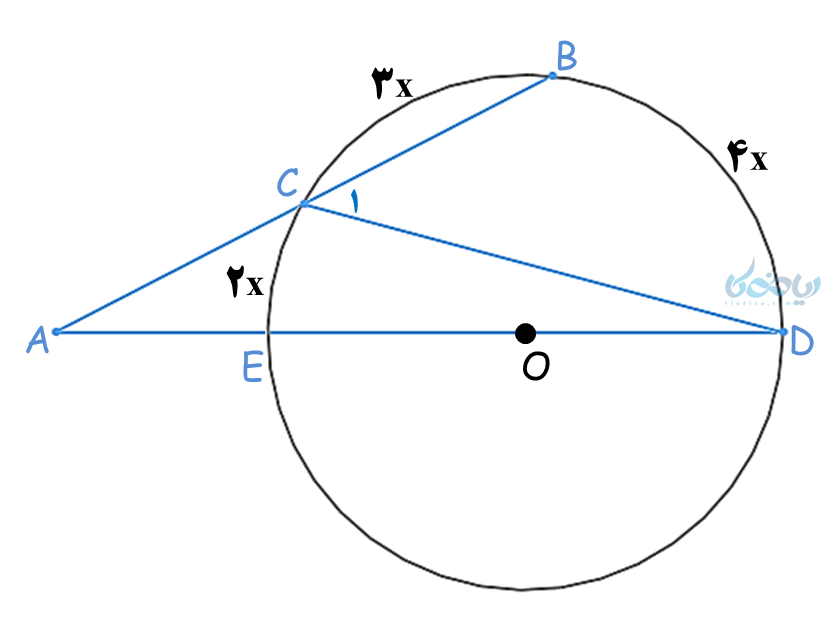
حل 3:
در شکل، اندازه کمان‌ها برحسب \( x \) داده شده است؛ برای محاسبه \( x \) از این نکته استفاده می‌کنیم که مجموع سه کمان نشان داده شده برابر با °180 است، چون نیم‌دایره را تشکیل می‌دهند؛ بنابراین:
\(\Large\ 2x+3x+4x=180° \)
\(\Large\ 9x=180° \)
\(\Large\ x=20° \)
زاویه‌های \(\Large\ \hat C_1 \) و \(\Large\ \hat D \) ، زوایای محاطی دایره هستند و اندازه آن‌ها برابر با نصف کمان روبروی آن‌هاست:
\(\Large\ C=\frac{\stackrel \frown {BD}}{2} \)
\(\Large\ C=\frac{4x}{2}=2x \)
\(\Large\ D=\frac{\stackrel \frown {CE}}{2} \)
\(\Large\ D=\frac{2x}{2}=x \)
از سوی دیگر در مثلث \( \Large ACD \) ، \(\Large\ \hat C_1 \) زاویه خارجی مثلث بوده و برابر با مجموع دو زاویه غیر مجاور (یعنی \( \Large \hat A \) و \( \Large \hat D \)) میباشد (یادآوری: فصل سوم، درس پنج کتاب درسی)
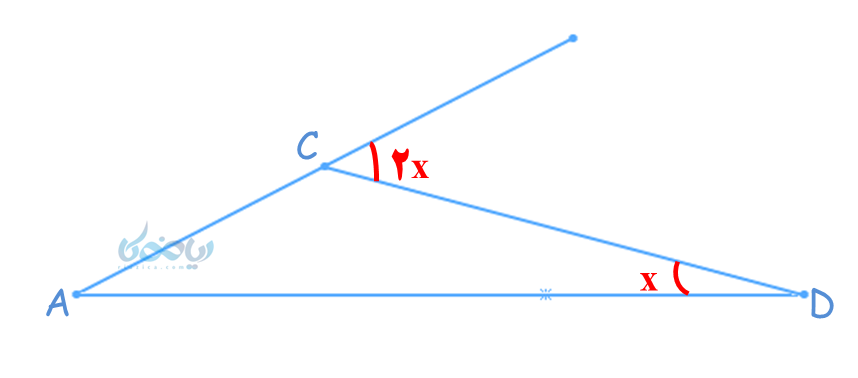
\(\Large \hat A+ \hat D= \hat C_1 \)
\(\Large \hat A+x=2x \)
\(\Large \hat A=x=20° \)
مثال 4 (یک مثال ترکیبی عالی با چاشنی زاویه های دایره):
طول کمان \( \Large \stackrel \frown {AB} \) در شکل زیر را محاسبه کنید.
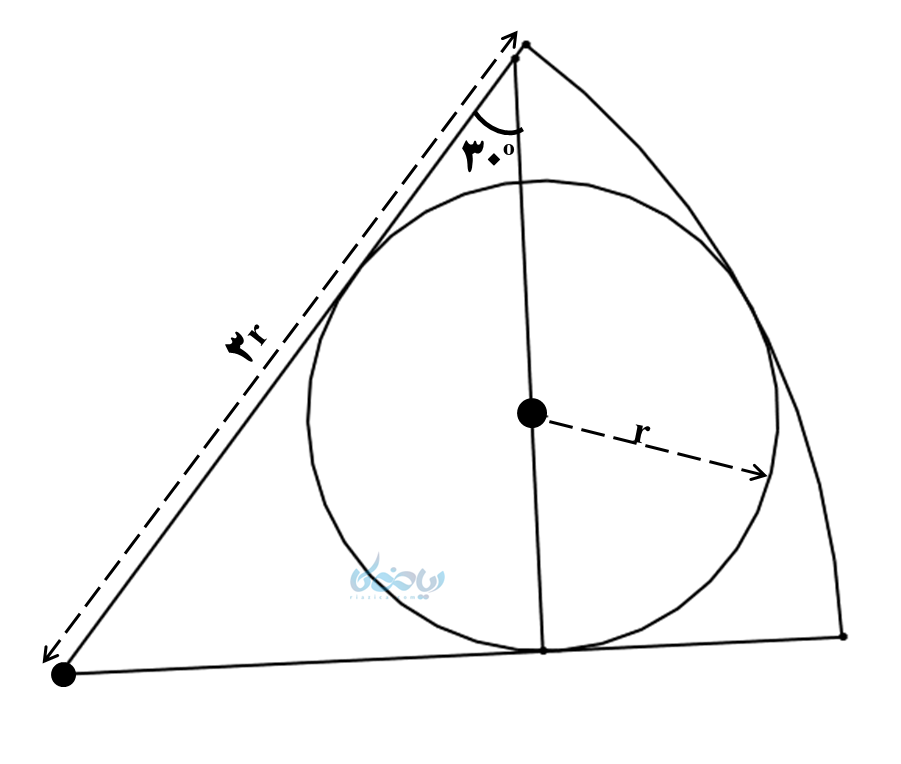
حل 4:
با دقت در شکل، مشاهده میشود که یک دایره کامل داریم که در یک بخش از دایره قرار گرفته است و اضلاع این بخش از دایره، بر دایره کامل مماس است. به خاطر دارید که در مبحث خط و دایره، گفته شد خط مماس در نقطه تماس بر شعاع دایره عمود است؟ از همین نکته برای حل این سؤال استفاده می‌کنیم:
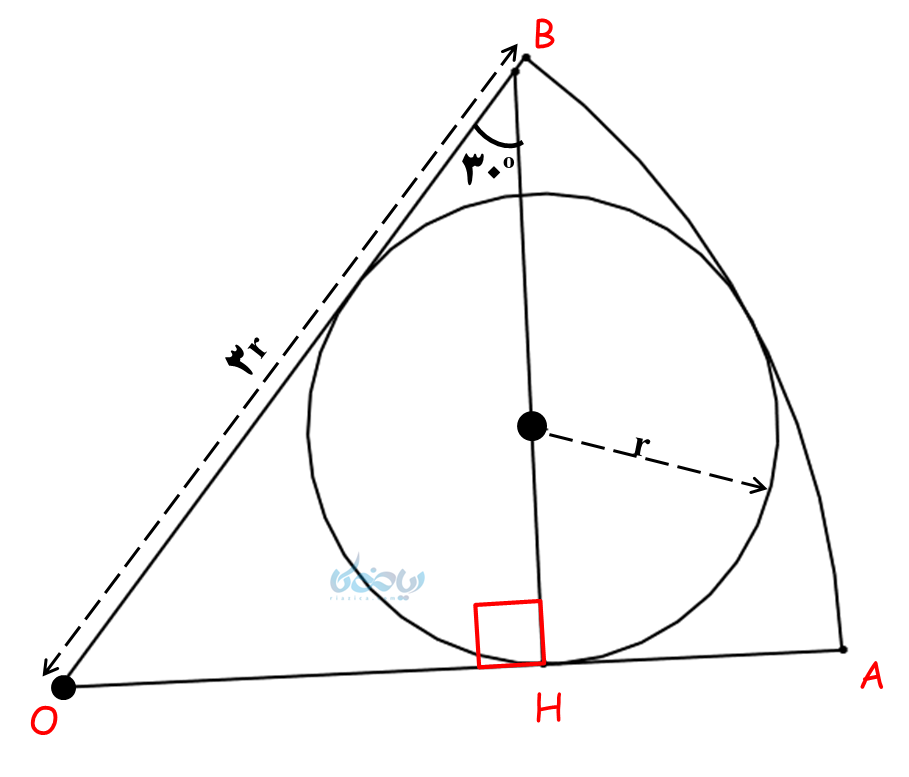
پس مثلث ACH قائم‌الزاویه بوده و بدین ترتیب می‌توانیم زاویه O را بدست آوریم. اما چرا زاویه O؟ با دقت در دایره ناقص، متوجه می‌شویم که زاویه O، یک زاویه مرکزی برای این دایره میباشد؛ پس برای محاسبه طول کمان لازم است آن را محاسبه کنیم.
\(\Large\ \hat O+\hat B+\hat H=180° \)
\(\Large\ \hat O+30+90=180° \)
\(\Large\ \hat O=60° \)
با توجه به ویژگی زاویه مرکزی، کمان AB نیز برابر با °60 میباشد. حال برای محاسبه طول کمان از تناسب گفته شده در بخش زاویه مرکزی استفاده می‌کنیم (توجه شود که محیط دایره کامل با شعاع 3r برابر است با \(\Large\ 2π×3r=6πr \) ):
\(\LARGE\ \frac {60}{360}= \frac {\stackrel \frown {AB}}{6πr} \)
\(\LARGE\ \stackrel \frown {AB}= \frac {60×6πr}{360} \)
\(\LARGE\ \stackrel \frown {AB}= πr \)
زنگ آخر کلاس زاویه های دایره : زاویه مرکزی و زاویه محاطی
در این درس، تعریف کمان و نحوه بیان بزرگی یک کمان را آموختیم؛ اکنون می‌توانیم طول و اندازه کمانی از دایره‌ای که به چند قسمت مساوی تقسیم شده را بدست آوریم. با زاویه های دایره از جمله زاویه مرکزی و زاویه محاطی و خصوصیات آن‌ها آشنا شدیم و با حل چند مثال، به کاربرد آن‌ها پی بردیم. این مبحث را برای همیشه در هندسه دایره به خاطر داشته باشید.
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاه‌ها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.
ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی هشتم به شما پیشنهاد می‌دهیم:
- زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعیها!
- اعداد صحیح ↔️➖➕– نمایش روی محور مختصات
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعیها!
- تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
- عدد اول ریاضی هشتم 1️⃣👨🎓 – کاملترین آموزشی که لازم داشتید.
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- خط و دایره : از سیر ➖ تا پیاز 🔴
- خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خطها در چهارراه زاویه!
- چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!
- ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
- فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارتهای جبری استفاده کن!
- حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
- بردار و مختصات ریاضی هشتم ➡️⬅️ – جهتدار و کامل!
- بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
- شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
- مثلث های هم نهشت 🌷🔺 گل سرسبد شکل‌های همنهشت!
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
- همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد میگیرید
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!
سلام تفاوت و شباهت زاویه محاطی و زاویه مرکزی چیه؟
با سلام وعرض ادب
شباهت هر دو داخل دایره هستن وتفاوت اینکه راس مرکزی روی مرکز دایره واقع شده ومحاطی روی محیط دایره واندازه زاویه مرکزی برابر کما روبروش هست ومحاطی نصف کمان روبرو
زاویه مماسی چی رابطه با زاویه محیطی دارد؟
سلام وعرض ادب
در کتاب هشتم زاویه مماسی ومحیطی نداریم
سلام
Oمرکز دایره و ABمماس بر دایره است. اگر کمان AMDبرابر 300°باشد اندازه زاویه مثلث OABرا بدست اورید
مثلث قائم الزاویه است
با سلام وعرض ادب
انتظار ندارید که بدون شکل پاسخ بدیم
به به
لذت میبرم از نوع آموزش
بسیار واضح و دلچسب
تشکر از همه عوامل
با سلام وعرض ادب
ممنون از لطف شما دوست عزیز
زاویه ی خارجی و داخلی چی؟؟؟؟؟
با سلام وعرض ادب
در چند ضلعی ها زاویه های داخل شکل را داخلی وزاویه های که امتداد اضلاع در خارج شکل می سازند را زاویه خارجی می گویند
سلام من یه رینگ دارم که قطر آن از لبه بیرونی رینگ ۳۶۸ میباشد و تو نقشه گفته شده باید زاویه ۳۰ درجه رو از قطر بکشم و همونجور که میدونید رینگ صفحه نیست که بشه از مرکز نقطه گرفت و انجام داد با پرگار . میشه راهنمایی کنید چجوری باید بدست بیارم زاویه ۳۰ درجه رو
سلام دوست عزیز
راهی که به نظر من میرسه یه مقوا به اندازه رینگ ببرید مرکزش رو پیا کنید ویه قطرش رو بکشید وبا نقاله یه زاویه ۳۰ درجه رسم کنید دقت کنید مرکز نقاله رو در مرکز بذارید ولبه نقاله رو روی قطر
خصوصیات زاویه محاطی و مرکزی چیست
با سلام وعرض ادب
اگه پست رو خوب بخونید به جواب سوالتون میرسید
اگر دایره درون یک ذوزنقه باشد محیط ذوزنقه چطور بدست می اید؟ (محیط دایره چهار نقطه ی اتصال با ذوزنقه دارد.)
با سلام وعرض ادب
اینجا بدون شکل نمیشه جواب داذ
سلام و عرض ادب.
خیلی عالی اگر ویدیو هم باشد بهتر میشود
سلام وعرض ادب
ممنون از نظر لطف شما
ویدیوهای پایه هشتم آماده شده وبه زودی روی سایت قرار میگیره
اگر AB و CD دو قطر دایره باشند ثابت کنید AC = BD
ببین
دو قطر دایره یعنی اینکه زاویه ها متقابل به راس هستن
پس یعنی زوایه های مربوط به کمان ها باهم برابره یعنی کمان هایی که به وجود میاد هم برابر میشن. پس وقتی کمان ها برابر میشن وتر های Ac و Bd هم با هم برابرند. ??
میتونیم بر اساس هم نهشتی مثلث هاپیش بریم
چون قطر دایره هستن پس نصف اونها شعاع دایره هست و همینطور ضلع مثلث هستش
چون که شعاع دایره هستن پس همه با هم برابر میشن و همینطور چون متقابل به راس میشه زوایه های متقابل به راس هم برابر میشن پس نتیجه میشه که مثلث ها به حالت
(ض ز ض) همنهشت هستند??
با سلام وادب ممنون از پاسخگویی شما
با عرض سلام و خسته نباشید خدمت شما استادان گرامی.با عرض پوزش,بخشید از هر درس چند ویدیو به صورت رایگان موجود است؟اخه داخل بعضی از درس ها ویدیو داشتین میخواستم بدونم برای دیگر درس ها ویدیو نمی زارین؟با سپاس از زحمات شما
سلام دوست عزیز
خیر ویدیو‌نداریم ولی پکیج ویدیویی هشتم موجود هست
پوزش مجدد,میشه بگید جواب این چند میشه؟ (سه رادیکل پنجاه منهای رادیکال هجده)
۱۵رادیکال۲ منهای ۳رادیکال ۲
پس جواب میشه ۱۲رادیکال۲
ممنون از پاسخگویی شما
در مثال ۴ چطور تشخیص دادین که زاویه O یه زاویه‌ی مرکزیه؟
سلام دایره بزرگتر که یک قطاع آن رسم شده در آن oمرکز دایره هست