آموزش ریاضی پایه هشتم
رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
خرداد
سال‌ها قبل دانشمندی به نام فیثاغورس کاری کرد کارستون! توی مثلث قائم‌الزاویه رابطه‌ای بین اضلاع پیدا کرد که بهش رابطه فیثاغورس میگن؛ البته بعضی‌ها اشتباهی بهش رابطه فیثاغورث هم میگن! در این درس‌نامه از سری آموزش ریاضی پایه هشتم ابتدا مرور کوتاهی بر مثلث قائم‌الزاویه و اجزای آن خواهیم داشت و سپس به معرفی رابطه فیثاغورس پرداخته و با استفاده از می‌توانیم خطی به طول یک عدد رادیکالی رسم کنیم.
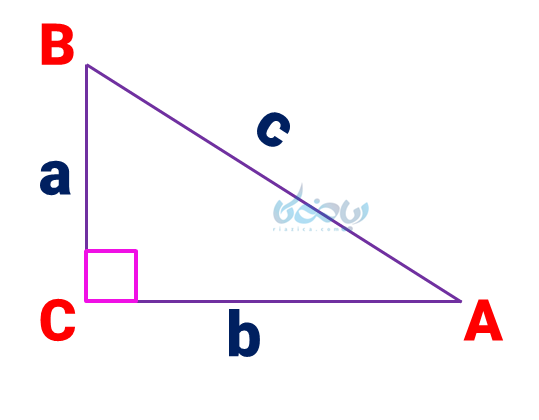
مثلث قائم‌الزاویه
مثلثی است که دو ضلع آن بر هم عمودند؛ یعنی دارای یک زاویه قائمه (°90) باشد. (زاویه \( \Large \hat C \) در شکل پایین). این نوع از مثلث در مباحث مختلف مثلثات مانند روابط بین نسبت‌های مثلثاتی بسیار پرکاربرد است.
وتر مثلث قائم‌الزاویه
وتر بزرگترین ضلع مثلث قائم‌الزاویه است که روبروی زاویه قائمه قرار دارد. (ضلع \( \Large c \) در شکل پایین)
اضلاع قائمه
به دو ضلع عمود بر هم در مثلث قائم‌الزاویه، اضلاع قائمه گفته میشود. (ضلعهای \( \Large a \) و \( \Large b \) در شکل پایین)
رابطه فیثاغورس
رابطه میان مجذور (مربع) اندازه ضلعهای مثلث قائم‌الزاویه به رابطه فیثاغورس معروف است. توجه کنید که این رابطه مخصوص مثلث‌های قائم‌الزاویه است، نه هیچ مثلث دیگری! این رابطه بدین صورت است:
در هر مثلث قائم الزاویه، مجذور وتر با مجموع مجذورهای دو ضلع دیگر برابر است. به زبان ریاضی در مثلث زیر:
\( \Large c^2 = a^2 + b^2 \)
مثال 1: در مثلث زیر، مقدار \( \Large x \) را بدست آورید.
حل 1:
این مثلث، قائم‌الزاویه است، پس بین اضلاع آن رابطه فیثاغورس برقرار است. با نوشتن این رابطه می‌توانیم مقدار \( \Large x \) را بدست آوریم:
\( \Large x^2 = 6^2 + 8^2 \)
\( \Large = 36 + 64 = 100 \)
\( \Large → x = \sqrt {100} = 10 \)
مثال 2: پدر رضا می‌خواهد برای رفتن به پشت‌بام خانه نردبان بسازد. اگر فاصله زمین تا پشت بام 12 متر باشد و بخواهد پای نردبان تا دیوار 5 متر فاصله داشته باشد، این نردبان باید چند متری باشد؟
حل 2:
برای حل این مثال، بیایید ابتدا یک شکل از چیزی که سؤال از ما خواسته رسم کنیم:
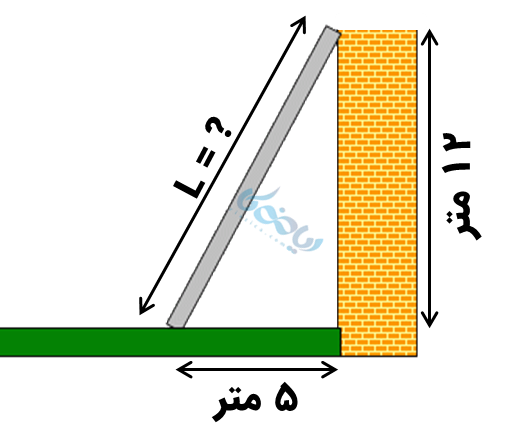
دقت کنید! این یک مثلث قائم‌الزاویه‌ای با وتری به طول نردبان (L) است. رابطه فیثاغورس را برای این مثلث می‌نویسیم:
\( \Large L^2 = 12^2 + 5^2 \)
\( \Large = 144 + 25 = 169 \)
\( \Large → L = \sqrt {169} = 13 \)
بنابراین برای بالا رفتن به نردبانی به طول 13 متر نیاز داریم.
عکس رابطه فیثاغورس
عکس رابطه فیثاغورس هم برقرار است. یعنی: اگر در یک مثلث، مجذور وتر با مجموع مجذورهای دو ضلع دیگر آن برابر باشد، آن مثلث قائم‌الزاویه خواهد بود.
مثال 3: تعیین کنید که کدام یک از مثلث‌های زیر قائم‌الزاویه است؟
حل 3:
طبق نکته بالا می‌دانیم که اگر در مثلثی مجموع مجذورهای دو ضلع برابر با مجذور ضلع سوم (یعنی ضلع بزرگتر: وتر) باشد، آن مثلث قائم‌الزاویه خواهد بود؛ پس برای هر مثلث رابطه فیثاغورس را می‌نویسیم:
\( \Large 3^2 + 4^2 \) (مثلث الف)
\( \Large = 9 + 16 = 25 \)
\( \Large 5^2 = 25 \)
با توجه به برقراری این رابطه برای مثلث (الف)، پس این مثلث قائم‌الزاویه است.
\( \Large 6^2 + 9^2 \) (مثلث ب)
\( \Large = 36 + 81 = 117 \)
\( \Large 11^2 = 121 \)
مثلث (ب) قائم‌الزاویه نیست، چون مجذور وتر با مجموع مجذورات دو ضلع دیگر برابر نیست
\( \Large \sqrt {13} \) و \( \Large \sqrt {12} \) باشد، طول ضلع دیگر چقدر خواهد بود؟
حل 4:
برای این مثلث، رابطه فیثاغورس را می‌نویسیم (دقت کنید که در اینجا وتر برابر با \( \Large \sqrt {13} \) است و طول ضلع سوم را \( \Large x \) گذاشته‌ایم):
\( \Large (\sqrt {13})^2 = (\sqrt {12})^2 + x^2 \)
\( \Large → 13 = 12 + x^2 \)
\( \Large x^2 = 1 → x = 1 \)
رسم پاره‌خطی به طول \( \Large \sqrt {a} \)؛ بهشت رابطه فیثاغورس
فرض کنید می‌خواهیم خطی به طول \(\Large \sqrt {a} \) رسم کنیم. برای این کار از رابطه فیثاغورس استفاده میکنیم. کافی است دو عدد پیدا کنیم که جمع مجذور این دو برابر با \(\Large (\sqrt {a})^2 \) یا همان \(\Large {a} \) شود؛ یعنی:
\(\Large x^2+y^2= (\sqrt {a})^2 \)
\(\Large x^2+y^2= a \)
پس اگر مثلث قائم‌الزاویه‌ای با دو ضلع قائمه \(\Large x \) و \(\Large y \) رسم کنیم، وتر آنها برابر با \(\Large \sqrt {a} \) خواهد شد.
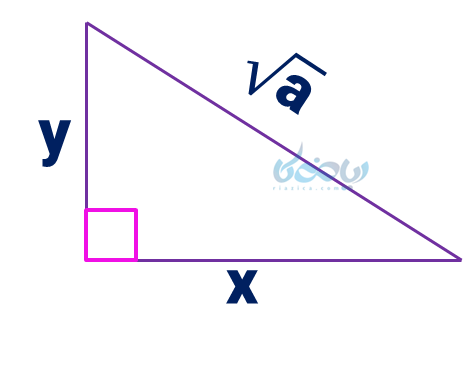
از این روش برای نمایش اعداد رادیکالی روی محور اعداد نیز استفاده میکنیم.
مثال 5: با توضیح روش، پاره‌خطی به طول \( \Large \sqrt {10} \) رسم کنید.
حل 5:
طبق روش گفته شده از رابطه فیثاغورس استفاده کرده و دو عدد مانند \(\Large x \) و \(\Large y \) پیدا میکنیم که مجموع مجذورهای آن دو برابر با \(\Large \sqrt {10} \) باشد؛ (به زبان ریاضی):
\(\Large x^2+y^2= (\sqrt {10})^2 \)
\(\Large → x^2+y^2= 10 \)
اگر به جای \(\Large x \) و \(\Large y \)، اعداد 1 و 3 قرار دهیم؛ این رابطه برقرار میشود:
\(\Large 1^2+ 3^2 = 1+9 = 10 \)
\(\Large L^2 = 10 → L = \sqrt {10} \)
بنابراین در مثلث قائم‌الزاویه زیر، طول وتر (پاره‌خط آبی رنگ) برابر با \( \Large \sqrt {10} \) خواهد بود:
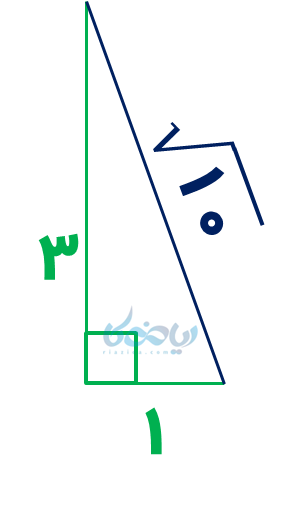
رسم مثلث‌های متوالی برای رسیدن به پاره‌خطی به طول \( \Large \sqrt {a} \)
گاهی لازم است برای رسم پاره‌خطی به طول یک عدد رادیکالی، چند مثلث قائم‌الزاویه رسم کنیم. با یک مثال، این روش را توضیح می‌دهیم:
اگر بخواهیم از روش گفته شده پاره‌خطی به طول \( \Large \sqrt {7} \) رسم کنیم، آیا می‌توان تنها از یک مثلث قائم‌الزاویه و رابطه فیثاغورس استفاده کرد؟
خب! بیایید امتحان کنیم. دو عدد پیدا میکنیم که مجموع مجذورهای آنها برابر با 7 باشد:
- اگه طول یکی از ضلع‌ها 1 باشه، اون یکی باید چند باشه؟ آها! \( \Large \sqrt {6} \)، چون
\(\Large 1^2 + (\sqrt {6})^2= 1+6=7 \)
- بازم راه هست؟ بله! اگه طول یکی از ضلع‌ها 2 باشه، اون یکی باید چند باشه؟ خب معلومه، \( \Large \sqrt {3} \)، چون
\(\Large 2^2 + (\sqrt {3})^2= 4+3=7 \)
اگر ضلع‌ها را \( \Large 2 \) و \( \Large \sqrt {3} \) در نظر بگیریم:
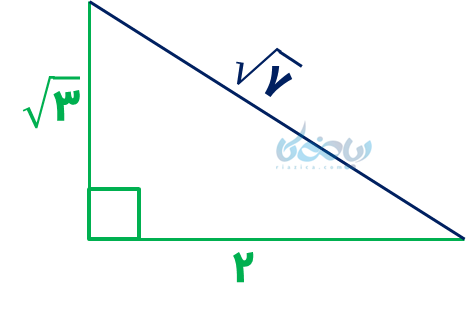
خب! همونطور که می‌بینید اول باید \( \Large \sqrt {3} \) رسم بشه (مثلث قائم‌الزاویه با اضلاع قائمه \( \Large 1 \) و \( \Large \sqrt {2} \) ):
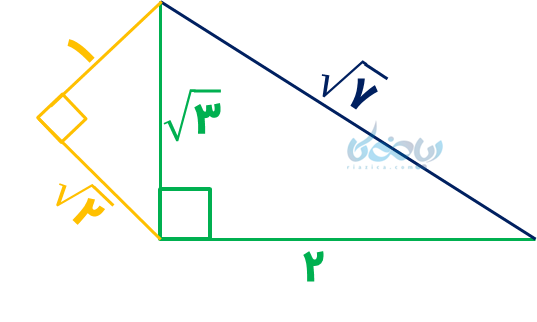
باز هم عددرادیکالی! پس باید \( \Large \sqrt {2} \) رسم بشه (مثلث قائم‌الزاویه با اضلاع قائمه \( \Large 1 \) و \( \Large 1 \) ):
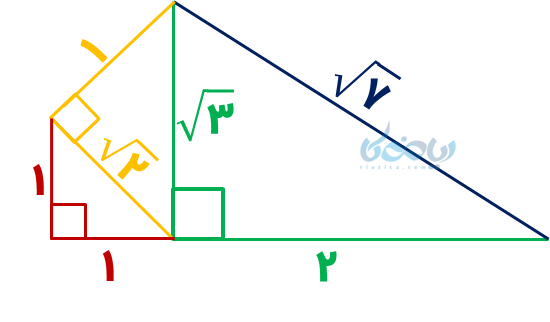
مشاهده کردید که برای رسم پاره‌خطی به طول \( \Large \sqrt {7} \)، از 3 مثلث قائم‌الزاویه متوالی استفاده کردیم. پس وقتی از شما پاره خطی به طول\( \Large \sqrt {7} \) می خواهند ابتدا مثلثی قائم‌الزاویه با اضلاع قائمه \( \Large 1 \) و \( \Large 1 \) رسم کرده سپس روی وتر آن مثلث قائم‌الزاویه با اضلاع قائمه \( \Large 1 \) و \( \Large \sqrt {2} \) رسم کنید و بعد روی وتر آن مثلث قائم‌الزاویه با اضلاع قائمه \( \Large 2 \) و \( \Large \sqrt {3} \) را بکشید
توجه: با این روش، هرچه جلو برویم و عدد رادیکالی داشته باشیم، باز هم باید مثلث قائم‌الزاویه و رابطه فیثاغورس را بکار ببریم.
مثلث‌های متوالی معروف!
مثلث‌های شکل زیر را در نظر بگیرید که در آن نحوه رسم 4 خط با طول‌های رادیکالی مختلف (به همان روشی که توضیح دادیم) نشان داده شده است. با استفاده از این روش می‌توان پاره‌خط‌هایی با هر طول رادیکالی را رسم کرد.
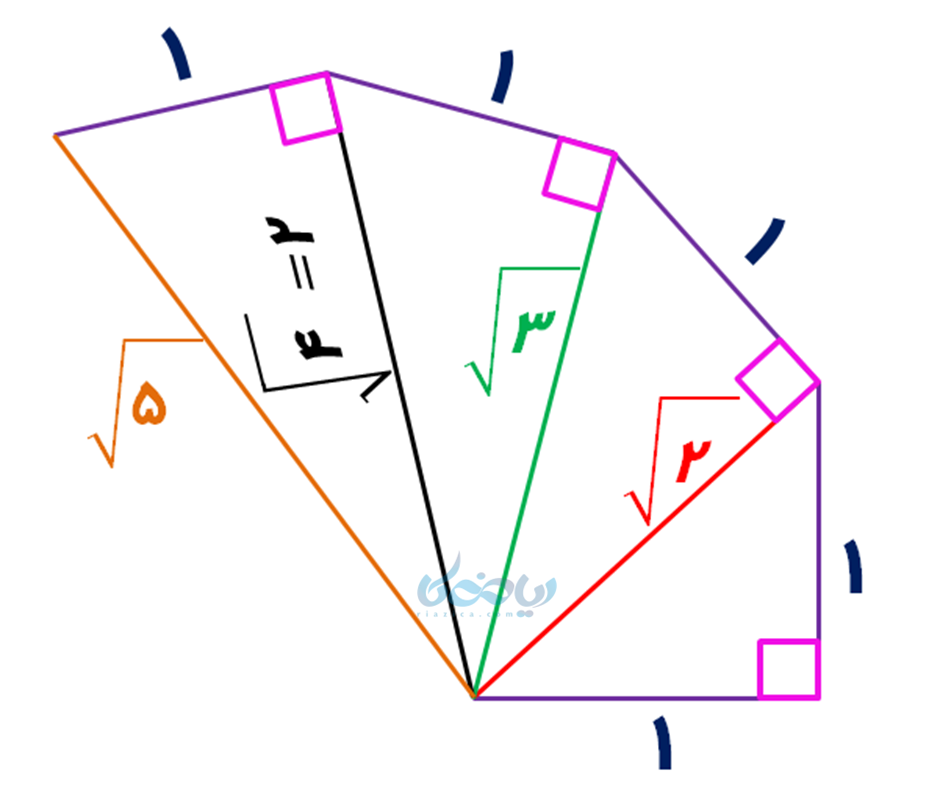
مثال 6: زهرا می‌خواهد به کمک قسمتی از دایره به شکل زیر، مخروطی به ارتفاع 2 سانتی‌متر بسازد. قاعده مخروط (دایره) را برای او رسم کنید.
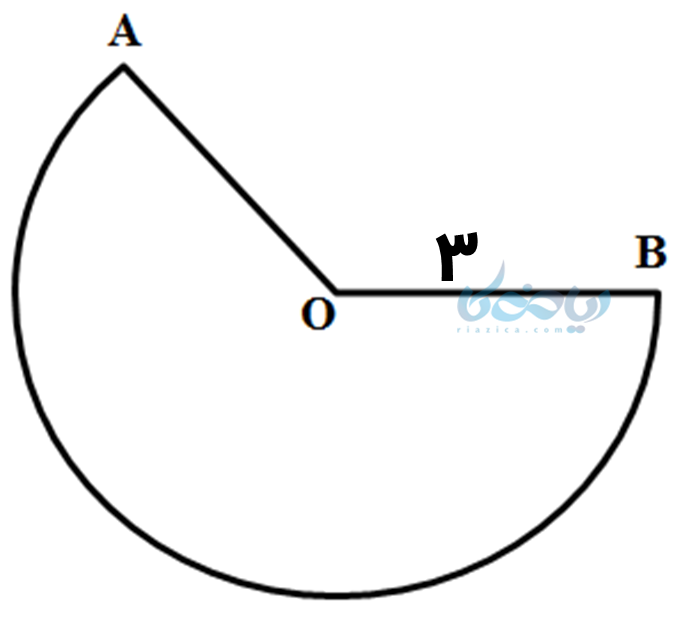
حل 6:
اگر در دایره ناقص بالا نقاط \( \Large A \) و \( \Large B \) را به هم برسانیم، یک حالت قیفی شکل (مخروطی) بصورت زیر ایجاد میشود که دایره قرمز رنگ زیر این قیف، قاعده مخروط خواهد بود:
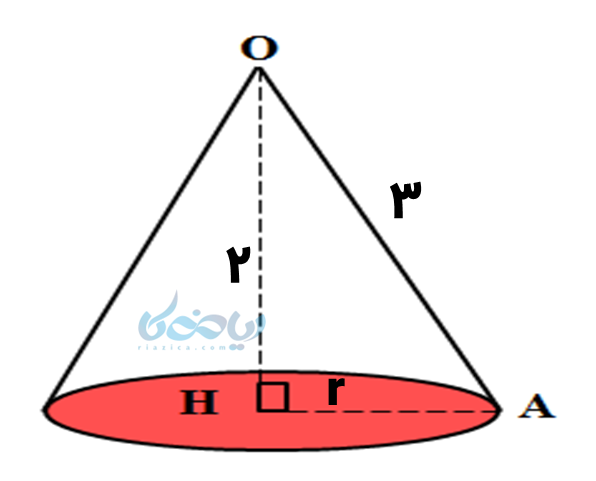
دقت کنید که چون ارتفاع مخروط بر قاعده عمود است، مثلث قائم‌الزاویه ایجاد شده و می‌توانیم از رابطه فیثاغورس برای بدست آوردن شعاع قاعده (\( \Large r \)) استفاده کنیم:
\(\Large r^2 + 2^2= 3^2 \)
\(\Large → r^2 + 4= 9 \)
\(\Large → r^2 = 9 – 4 = 5 \)
\(\Large → r = \sqrt{5} \)
می‌خواهیم قاعده مخروط را برای زهرا رسم کنیم که دایره‌ای به شعاع \( \Large \sqrt{5} \) است. یادمان که نرفته؟ برای این کار از مثلثی با اضلاع قائمه 1 و 2 استفاده میکنیم:
\(\Large 1^2 + 2^2= 1+4=5 \)
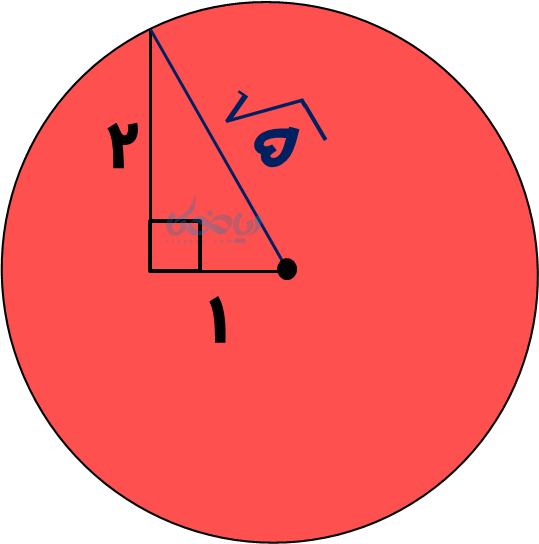
با رسم این پاره‌خط می‌توانیم دو طرف پرگار را روی دو سر پاره‌خط قرار دهیم و دایره را رسم نماییم.
ویدیو آموزش رابطه فیثاغورس ریاضی هشتم
در این ویدیو به طور کامل رابطه فیثاغورس آموزش داده شده است.
زنگ آخر کلاس رابطه فیثاغورس
در این درس‌نامه پس از مرور اجزاء یک مثلث قائم‌الزاویه، با رابطه مهمی در مثلثات به نام رابطه فیثاغورس آشنا شدیم؛ مطمئن باشید حالا حالاها با این فرمول سر و کار خواهیم داشت. همچنین با استفاده از این رابطه پاره‌خط‌هایی به طول اعداد رادیکالی رسم کردیم. حل مثال‌های زیاد در این درس قطعاً در آینده کمک زیادی به ما خواهد کرد.
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاه‌ها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.
ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی هشتم به شما پیشنهاد می‌دهیم:
- زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعیها!
- اعداد صحیح ↔️➖➕– نمایش روی محور مختصات
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعیها!
- تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
- عدد اول ریاضی هشتم 1️⃣👨🎓 – کامل‌ترین آموزشی که لازم داشتید.
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- خط و دایره : از سیر ➖ تا پیاز 🔴
- خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خطها در چهارراه زاویه!
- چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!
- ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
- فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارتهای جبری استفاده کن!
- حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
- بردار و مختصات ریاضی هشتم ➡️⬅️ – جهتدار و کامل!
- بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
- شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
- مثلث های هم نهشت 🌷🔺 گل سرسبد شکلهای همنهشت!
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
- همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد میگیرید
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!
عالییییییییییی بود بخدا
سلام و عرض ادب
ممنون از انرژی و پیام پرمهرتون.
موفق باشید
خیلی خوب بودددددد مرسی
سلام و عرض ادب
ممنون از انرژی و پیام پرمهرتون.
موفق باشید
خیلی خوب بود اگر هم رایگان میزاشتین دانلود کنیم عالی تر هم میشد.
دست سازنده این سایت درد نکند.
با عرض سلام وروز به خیر
خوشحالیم که براتون مفید بوده دوست عزیز ما وقت وهزینه زیادی برای راه اندازی این سایت انجام داده ایم پس منطقی هست که بخواهیم قسمتی از هزینه هایمان را جبران کنیم ما تنها سایت ریاضی هستیم که خط به خط کتاب درسی را به زبان ساده وتوسط اساتید مجرب تدریس کرده ایم وعلاوه بر اجر معنوی باید سود مادی هم برای ما داشته باشد
یعنی به تمام معنا عالییییییییییییییی بود
عالییییییییی.
دستتون درد نکنه، خیلی خیلی ممنونم
با عرض سلام واحترام خوشحالیم که براتون مفید بوده این پست رو به دوستانتون هم معرفی کنید
عالی بود عالیییی
باسلام
موجب دلگرمی ما هست
اخه صبر کن شما یه پی دی افو میدی 39 هزار تومن من یه دفترچه ی فیساغورس خریدم به 39 هزارتازه اون کاغذه اما من باید اینجا دانلود کنم چاپ کنم نمیشه که یکم گرونه
سلام و عرض ادب
اولا ما کل کتاب به صورت پی دی اف براتون قرار دادیم
دوما شما کتاب های بیرون مشاهده کنید، کمتر از ۹۰ هزار تومان پیدا نمیشه که سراسر مطالب به شما یاد بدهند
موفق باشید
سوال اول رابطه فیثاغورس در هر مثلثی برقرار است ؟؟
با عرض سلام
فقط در مثلث قائم الزاویه برقرار است.
موفق باشید
سلام ببخشید میشه قسمت های که به زبان انگلیسی نوشته شده را به فارسی بنویسید
با عرض سلام و ادب
منظورتون کجاست ؟ جآیی انگلیسی نوشته نشده
رابطه فیثاغورسدر مثمثلث هایی برقرار است که دو زاویه تند آن جای خالی یکدیگرباشند
با سلام
که مجموع دو زاویه تند آنها ۹۰ درجه باشد
سوال من توش نبود
با سلام وعرض ادب
میشه سوالتون رو مطرح کنید؟
سلام اگر در یک مثلث قائم الزاویه فقط اندازه یک ضلع را داشته باشیم و دو ضلع دیگر نابرابر باشند چگونه اندازه آن دو ضلع را بدست آوریم؟؟
با سلام وعرض ادب
باید حتما اندازه دو ضلع را داشته باشیم مگر اینکه اندازه یک زاویه تند از مثلث را داشته باشیم واز راه مثلثاتی که در پایه دهم میخوانید دو ضلع دیگر را پیدا کنیم یا مثلا اگر اندازه یک زاویه ۳۰ درجه باشد ضلع روبرویش نصف وتر میشود
خیلی عالی بود ♥️♥️
ممنونم از شما خیلی کاربردی و مفید بود
??
ولی کاش پولی نبود و رایگان بود
با سلام واحترام
ممنون و خوشحالیم که براتون مفید بوده
دوست عزیز شما همین مبحث رو اگر بخواهی با یه معلم خصوصی بگذرونی ده برابر باید هزینه کنید یاد بگیریم برای پیشرفت هزینه کنیم به اندازه کافی هم مطلب رایگان در سایت هست
برای اطلاع از جشنواره ها ومطالب بیشتر ما رو در اینستا دنبال کنید
پیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام اگر هر دو اضلاع قائمه یکیش x و اون یکی y باشه ، وتر ۱۰ و ضلع روبه رویِ قائمه از داخل ۳۰ باشه ، یعنی ۳۰ داخل نوشته شده باشه ، چطوری محاسبه میشه؟
با سلام
ضلع روبروی زاویه ۳۰ درجه نصف وتر هست پس یک ضلع ۵ ووتر ۱۰ با فیثاغورس حساب کنید
سلام وقتتون بخیر.اگه دریک مثلث قائم الزاویه یک قاعده ۲۴xویکیش ۷xباشه و وتر ۲۵ مقدارxطبق رابطه فیثاغورس چجوری بدست میاد؟
با سلام
رابطه فیثاغورس حل کن یه معادله به دست میاد معادله رو حل کن
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
ببخشید وقتی تو مثلث قائم الزاویه اندازه وتر را بده ما چجوری اندازه دو ضلع دیگه حساب کنیم؟
با سلام و روز به خیر
اگه فقط وتر رو بده واطلاعات دیگه ای نداده باشه ومثلث خاطی نباشه نمیشه دو ضلع دیگه رو بدست آورد
سلام عالی بود اما قسمت دوم حل رابط فیساقرسه متوجه نشدم که چگونه به دست میاد
با سلام وعرض ادب
ممنون از شما دقیقا کجا رو متوجه نشدید ؟
خیلی عالی بود شما خیلی خوب این رابطه رو عمقی درس میدید
ممنون خدا قوت
با سلام وعرض ادب
ممنون از لطف وتوجه شما دوست عزیز
توضیحات کاملی بود
با سلام واحترام ممنون از نظر شما
میشه یه توضیح کلی از کتاب نهم رو بگین ؟
با سلام وعرض ادب
فقط میتونم بگم نه تا فصل که برا ابن ترم پانزده نمره از ترم دوم مباد وتمرکزتون رو بیشتر روی مباحث ترم دوم بذارید
بسیار عالی
با سلام وعرض ادب
ممنون از لطف شما
سلام
خسته نباشید.
ممنون بابت سایت عالی و خوبتون❤
با سلام احترام
ممنون از نگاه خوب شما
سلام خسته نباشید پاره خطی به طول رادیکال ۱۸ رسم کنید.
رادیکال ۱۸ :
۶۴ :۸
و
۱۰۰ :۱۰
اوک؟?
همینو بگم که خیلی عالی بود
با سلام وادب
ممنون از نگاه شما
سلام خدایی خیلی مفید بود فقط یکمی سوالاتش رو بیشتر کنید لطفاً
انشالله به زودی
با سلام . دمتون گرم واقعا من مدرسه تیزهوشان ایت الله مشکینی ( میری ) قم درس میخونم و با وجود معلم ریاضی ای که داشتم بیشتر دانش آموزان نتونستیم رابطه فیثاغورس رو یاد بگیریم اما من امروز وقتی از ستیتتون بازدید کردم فقط با خوندن چند خط تونستم رابطه فیثاغورس رو یاد بگیرم و برای دوستامم فرستادم واقعا عاای با انرژی به کارتون ادامه بدید عالیییی ????????
با سلام دوست عزیز
ممنون از ابراز محبت شما واقعا خوشحالیم که سایتبرا همه مفید هست
عالی بود
سلام دوست عزیز
ممنون از نگاه شما
عالی
صلام خیلی خوب بود
میشه لطفا جمع فیثاغورسی اعدا طلایی هم بزارید
خیلی عالی بود ممنون
سلام وقت بخیر سوال من توش نبود و بعدشم معلم ما خانم صفایی سه تا فرمول بهمون داده که دوتاشون یکی باید کم کنزم ودیگر هم جمع کنیم و سومی هم این هستش جریان این دوتا فرمول چی هستش
سلام دوست عزیز
فیثاغورث یه فرموله
ولی معلمان عزیز برای اینکه بچه ها بهتر یاد بگیرن دو تا نتیجه از این فرمول میگیرن اونم اینه که اگه وتر رو بخواهید مجذور دو ضلع دیگه رو جمع کنید ولی اگه وتر رو داشته باشید یکی از ضلعهای زاویه قائمه رو بخواهید مجذور وتر رو از مجذور اون یکی ضلع کم میکنیم