آموزش ریاضی پایه هشتم
تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
شهریور
گویا قرار است در این جلسه به تعریف اعداد گویا بپردازیم؟! ولی به نظر من هرچقدر از عددهای گویا تعریف کنیم، باز هم کم است، آخر این عددها مادر خیلی از اعدادی است که تا به حال خوانده‌ایم. احترام مادر هم واجب است؛ می‌پرسید چرا مادر؟ عجله نکنید، در این درس به آن هم خواهیم رسید. تا ارتباط تصویری مجموعه اعداد صبر کنید.
در این درس از مجموعه آموزش ریاضی پایه هشتم ، در مورد اعداد گویا صحبت خواهیم کرد. پس از تعریف اعداد گویا و نوع خاص آن (اعداد اعشاری)، ارتباط مجموعه اعداد مختلف، ساده کردن کسرها، مقایسه اعدادگویا با هم، نوشتن چند عدد گویای مساوی توضیح داده خواهد شد. حل مثال‌های این درس قطعاً به تسلط شما بسیار کمک خواهد کرد.
تعریف اعداد گویا
به هر عددی که بتوان به صورت کسر \( \Large \frac{a}{b} \) نوشت که در آن \( \Large a \) و \( \Large b \) هر دو عدد صحیح باشند و \( \Large b \ne 0 \)، عدد گویا گفته میشود.
مجموعه اعداد گویا، با حرف انگلیسی \( \Large Q \) نشان داده میشود. لازم به ذکر است که تعریف گفته شده در بالا، با نمادهای ریاضی بصورت زیر نوشته شده است:
\( \Large Q= \) { \( \Large \frac{a}{b} \mid a,b \in Z , b \ne 0 \) }
به عنوان نمونه، \( \Large \frac{2}{3} \) و \( \Large -\frac{8}{5} \) اعداد گویا هستند؛ اما \( \Large \frac{4}{0} \) تعریف نشده است (مخرج نباید صفر باشد).
تبدیل عدد گویای کسری به عدد مخلوط و بالعکس
عدد مخلوط، نحوه دیگر نمایش عدد کسری است که به شکل \( \Large c\frac{a}{b} \) نوشته میشود (\( \Large c \) هم مانند \( \Large a \) و \( \Large b \)، یک عدد صحیح است). وقتی اندازه یک عدد بزرگتر از یک باشد (یعنی صورت کسر از مخرج آن بزرگتر باشد)، می‌توان بخش صحیح آن را جدا کرد (\( \Large c \)) و مابقی را بصورت کسری در سمت راست آن نوشت.
عدد کسری همان نحوه نمایشی است که در تعریف اعداد گویا یاد گرفتیم. همچنین برای تبدیل عدد مخلوط به عدد کسری، قسمت صحیح را در مخرج ضرب کرده و با صورت جمع میکنیم و به مخرج تقسیم میکنیم؛ یعنی:
\( \LARGE c\frac{a}{b} = c + \frac{a}{b} \)
\( \LARGE = \frac{(c×b)+a}{b} \)
مثال 1: اعداد کسری \( \Large -\frac{2}{1} \)، \( \Large \frac{5}{2} \) و \( \Large -\frac{4}{3} \) را بصورت عدد مخلوط و عدد \( \Large 3\frac{2}{5} \) را بصورت عدد کسری نشان دهید.
حل 1:
برای تبدیل عدد کسری به مخلوط باید ببینیم چه مقدار صحیحی از کسر بیرون می‌آید (\( \Large c \)). به عبارتی،حاصل تقسیم صورت به مخرج پشت کسر و باقی‌مانده آن در صورت قرار می‌گیرد و مخرج هم دست‌نخورده باقی می‌ماند.
\( \Large -\frac{2}{1} = -2 \) ؛ در واقع، (2-) قسمت صحیح داریم و هیچ کسری باقی نمی‌ماند.\( \LARGE \frac{5}{2} = \frac{4}{2} + \frac{1}{2} \)
\( \LARGE = 2 + \frac{1}{2} = 2\frac{1}{2} \)
\( \LARGE -\frac{4}{3} = \frac{-3}{3} + \frac{-1}{3} \)
\( \LARGE = -1 – \frac{1}{3} = -1\frac{1}{3} \)
برای تبدیل عدد مخلوط به کسری ( مشابه تعریف اعداد گویا ) نیز از روش گفته شده در بالا استفاده میکنیم:
\( \LARGE 3\frac{2}{5} = 3 + \frac{2}{5} \)
\( \LARGE = \frac{(3×5)+2}{5} = \frac{17}{5} \)
نکته: علامت منفی عدد مخلوط را می‌توان در صورت، مخرج یا قبل از عدد آورد.
عدد اعشاری- برمی‌گردیم به تعریف اعداد گویا با مخرج 10
هر عدد اعشاری، در واقع یک عدد گویا با مخرج 10 است؛ کافی است در تعریف اعداد گویا به جای مخرج، عدد 10 قرار دهید. به عنوان مثال تعدادی عدد اعشاری در زیر بصورت گویا نشان داده شده است:
\( \LARGE -1/2 = -1\frac{2}{10} \)
\( \LARGE 0/5 = \frac{5}{10} \)
\( \LARGE 2/9 = 2\frac{9}{10} \)
ارتباط تصویری مجموعه اعداد
تا به حال با مجموعه اعدادی مانند مجموعه اعداد صحیح یا همین مجموعه اعداد گویا آشنا شده‌ایم. برای آن‌که این مجموعه اعداد بهتر در ذهن ما بماند و همچنین چگونگی ارتباط مجموعه اعداد را بدانیم، نمودار زیر بسیار به ما کمک می‌کند (البته نگران مجموعه‌هایی که تا به حال نخوانده‌اید، نباشید).
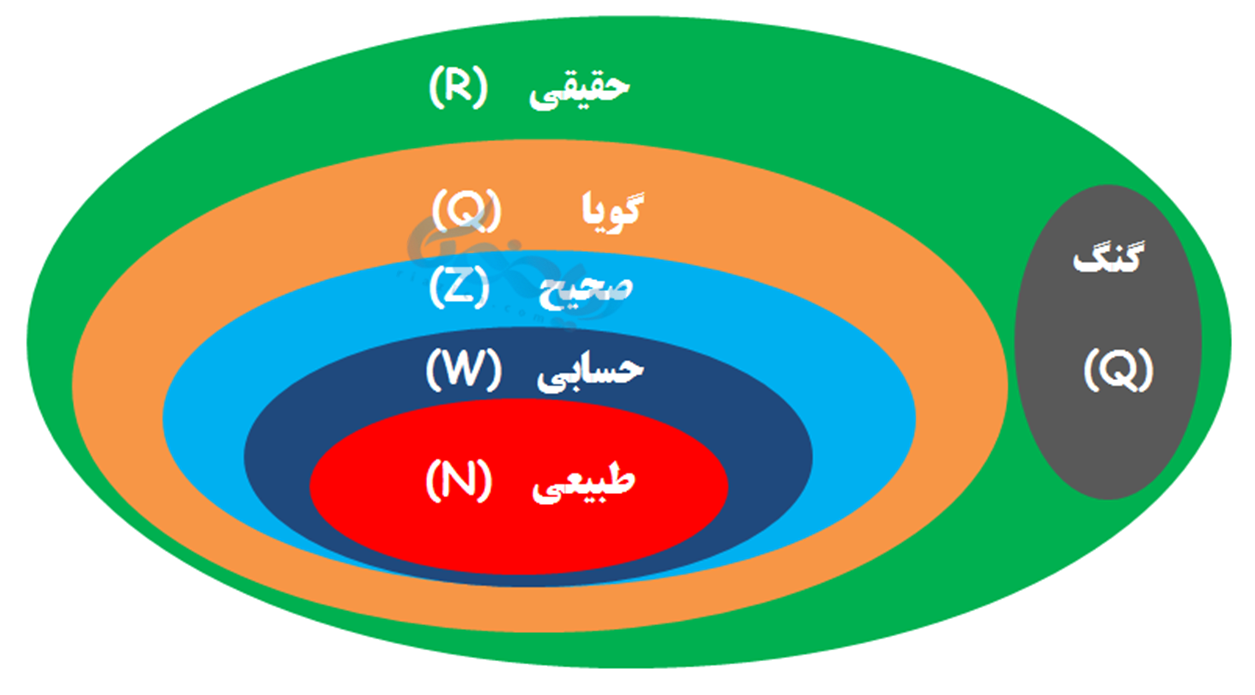
این تصویر نشان می‌دهد که مجموعه اعداد حقیقی از مجموعه اعداد گویا و گنگ تشکیل شده است. اعداد طبیعی زیرمجموعه اعداد حسابی و آن هم زیرمجموعه اعداد صحیح است. مجموعه اعداد صحیح زیرمجموعه اعداد گویاست.
با توجه به این ارتباط، می‌توان به عنوان مثال گفت هر عدد صحیح یک عدد گویا نیز هست، یا هر عدد طبیعی، یک عدد صحیح هم محسوب میشود.
مثال 2: نشان دهید مجموعه اعداد صحیح، زیرمجموعه اعداد گویاست.
حل 2:
در واقع سؤال را اینطور ترجمه میکنیم: نشان دهید هر عدد صحیح، یک عدد گویاست، به عبارتی باید بتوانیم هر عدد صحیح را به صورت یک عدد گویا بنویسیم، یعنی به صورت کسر\( \Large \frac{a}{b} \) (به شرطی که \( \Large b \) صفر نباشد).
کدام عدد است که با تقسیم هر عدد به آن، حاصل تقسیم تغییر نمی‌کند؟ بله! عدد 1. پس میتوانیم هر عدد صحیح \( \Large a \) را به صورت \( \Large \frac{a}{1} \) بنویسیم؛ مثلاً می‌توان 4- را بصورت \( \Large -\frac{4}{1} \) نوشت. پس هر عدد صحیح، گویا هم هست و این، یعنی مجموعه اعداد صحیح، زیرمجموعه اعداد گویاست.
قرینه اعداد گویا
پس از تعریف اعداد گویا و همچنین آموختن نحوه ارتباط مجموعه اعداد، حالا نوبت به مطالبی در مورد عددهای گویا میرسیم. قرینه اعداد گویا هم مانند قرینه سایر اعداد است که در درس‌نامه جمع و تفریق اعداد صحیح بصورت دقیق آموزش داده شده است. برای محاسبه قرینه یک عدد کافی است علامت قبل از آن را تغییر دهیم؛ از طرفی قرینه عدد صفر، خود صفر است.
ساده کردن کسرها
برای ساده کردن کسر، ابتدا آن را با توجه به روش گفته شده در درس‌نامه جمع و تفریق اعداد صحیح برای تقسیم علامت‌ها، تعیین علامت میکنیم؛ سپس اگر هم صورت و هم مخرج به یک عدد بخش‌پذیر باشند، می‌توان آن‌ها را به آن عدد تقسیم کرد تا کسر ساده‌تر شود. این عمل را می‌توان تا جایی که صورت و مخرج به یک عدد مشترک بخش‌پذیر نباشد، ادامه داد.
مثال 3: کسرهای زیر را تا حد امکان ساده کنید:
الف) \( \Large \frac{20}{60} \) ب) \( \Large \frac{-13}{-39} \) ج)\( \Large \frac{126}{-90} \)
حل 3:
برای ساده کردن کسر، همان‌طور که گفته شد کافی است ببینیم صورت و مخرج هر دو بر چه عددی بخش‌پذیرند. سپس هر دو را به آن عدد تقسیم کنیم:
(الف)
همان‌گونه که می‌بینیم، هر دو عدد 20 و 60 به 10 بخش‌پذیرند؛ پس ابتدا هر دو را به 10 تقسیم میکنیم. سپس می‌بینیم باز هم می‌توان آن را ساده کرد، چون هر دو به 2 بخش‌پذیرند. با تقسیم اعداد 2 و 6 به دو، کسر به ساده‌ترین شکل نوشته میشود (چون دیگر نمی‌توانیم هر دو را به یک عدد تقسیم کنیم):
(ب)
ابتدا تعیین علامت میکنیم: (-) تقسیم بر (-) میشود (+):
(ب)
ابتدا تعیین علامت میکنیم: (+) تقسیم بر (-) میشود (-):
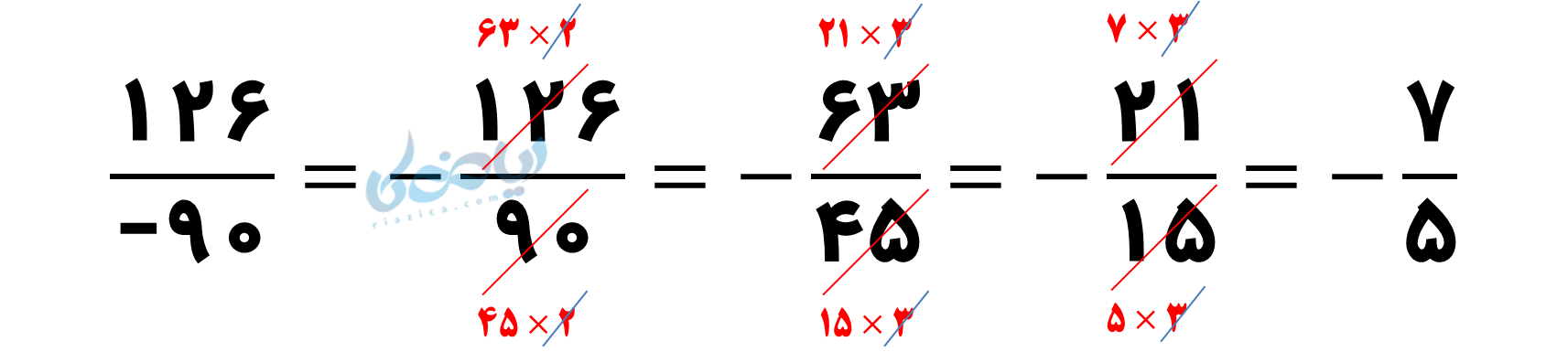
نکته : میتوانید ب.م.م صورت ومخرج را پیدا کنید خیلی سریع با یک مرحله تقسیم کسر را ساده کنید.
پیدا کردن چند عدد گویای مساوی
برای پیدا کردن چند عدد برابر با یک عدد گویا می‌توان صورت و مخرج را در یک عدد ثابت ضرب کرد؛ با این کار مقدار کسر هیچ تغییری نمی‌کند.
مثال 4: سه کسر مساوی با عدد گویای \( \Large -\frac {4}{14} \) بنویسید. آیا عدد \( \Large -\frac {2}{7} \) با این عدد برابر است؟
حل 4:
گفتیم با ضرب صورت و مخرج در یک عدد، اندازه آن عدد گویا با کسر اول برابر خواهد بود؛ پس بیشمار عدد کسری مساوی با آن می‌توان نوشت. برای این کار اعداد (2)، (3) و (10) را در صورت و مخرج عدد داده شده ضرب میکنیم:
\( \LARGE -\frac {4×2}{14×2} = -\frac {8}{28} \) (ضرب 2)
\( \LARGE -\frac {4×3}{14×3} = -\frac {12}{42} \) (ضرب 3)
\( \LARGE -\frac {4×10}{14×10} = -\frac {40}{140} \) (ضرب 10)
\( \LARGE -\frac {4×2}{14×2} = -\frac {8}{28} \) (ضرب 2)
برای این که ببینیم آیا عدد \( \Large -\frac {2}{7} \) نیز با عدد داده شده برابر است یانه، کافی است ببینیم با ضرب صورت و مخرج آن در یک عدد به آن میرسیم یا نه!
اگر دقت کنیم می‌بینیم که با ضرب صورت و مخرج \( \Large -\frac {2}{7} \) در عدد 2، به همان کسر \( \Large -\frac {4}{14} \) میرسیم. پس این دو عدد گویا با هم برابرند.
مقایسه اعداد گویا- کاربرد مهم تعریف اعداد گویا
برای مقایسه اعداد گویا با یکدیگر یا مرتب کردن اعداد گویا از کوچک به بزرگ و … به نکات ذیل توجه نمایید:
هر دو کسر مثبت
(الف) اگر مخرج دو کسر برابر باشد، کسری بزرگتر است که صورت بزگتری دارد.
(ب) اگر صورت دو کسر برابر باشد، کسری بزرگتر است که مخرج کوچکتری دارد.
(ج) اگر صورت یا مخرج دو کسر برابر نباشد، ابتدا مخرج مشترک گرفته و سپس مطابق حالت (الف) مقایسه میکنیم.
هر دو کسر منفی
(الف) اگر مخرج دو کسر برابر باشد، کسری بزرگتر است که صورت کوچکتری دارد.
(ب) اگر صورت دو کسر برابر باشد، کسری بزرگتر است که مخرج بزرگتری دارد.
(ج) اگر صورت یا مخرج دو کسر برابر نباشد، ابتدا مخرج مشترک گرفته و سپس مطابق حالت (الف) مقایسه میکنیم.
نکته 1: اعداد گویای مثبت از صفر بزرگتر و اعداد گویای منفی از صفر کوچکترند.
نکته 2: اگر یک کسر مثبت و کسر دیگری منفی باشد، همواره اعداد مثبت از منفی بزرگترند.
مثال 5: اعداد زیر را از بزرگ به کوچک مرتب کنید (از چپ به راست):
\( \Large 2 \) ، \( \Large -3/1 \)، \( \LARGE -\frac {31}{3} \)، \(\LARGE 1\frac {7}{6} \)، \( \LARGE \frac {5}{7} \)
حل 5:
با توجه به نکات بالا، ابتدا اعداد مثبت و منفی را از هم جدا میکنیم (چون هر عدد مثبتی از هر عدد منفی بزرگتر است):
\( \Large 2 \) , \( \LARGE 1\frac {7}{6} \) , \( \LARGE \frac{5}{7} \) (مثبت)
\( \Large -3/1 \) , \( \LARGE -\frac {31}{3} \)(منفی)
حالا اعداد مثبت را با هم و اعداد منفی را با هم مقایسه میکنیم:
(مقایسه اعداد مثبت):
یک عدد صحیح (\( \Large 2 \))، یک عدد گویا مخلوط (\( \Large 1\frac{7}{6} \)) و یک عدد گویا کسری (\( \Large \frac{5}{7} \)) داریم. برای آن که بتوانیم آن‌ها را با هم مقایسه کنیم، چون هیچ یک صورت یا مخرج برابر ندارند، مخرج مشترک می‌گیریم:
برای این کار ابتدا هر سه را بصورت کسری مینویسیم (توجه کنید که هر عدد صحیح، یک عدد گویا با مخرج 1 است):
\( \LARGE 2 = \frac {2}{1} \)
\( \LARGE 1\frac {7}{8} = \frac{(1×8)+7}{8} = \frac{15}{8} \)
\( \LARGE \frac{5}{7} \)
یادآوری ک.م.م(برای یاد آوری بدست آوردن ک.م.م به پست کوچکترین مضرب مشترک مراجعه کنید)
بنابراین مخرج کسرها به ترتیب 1، 8 و 7 است. بهترین مخرج مشترک چیست؟ بله! ک.م.م.
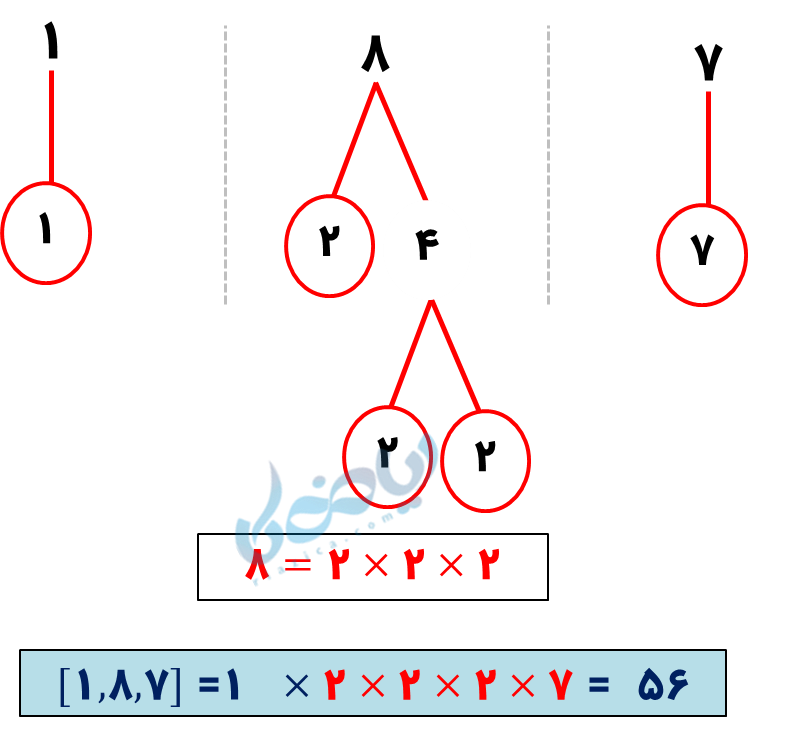
مطابق روش نمودار درختی (که در درس عدد اول آموزش داده شد)، ک.م.م این سه عدد برابر است با 56. پس مخرج مشترک آن‌ها برابر است با 56 و این کسرها به ترتیب برابرند با:
\( \LARGE \frac {2×56}{56} = \frac {112}{56} \)
\( \LARGE \frac {15×7}{56} = \frac {105}{56} \)
\( \LARGE \frac {5×8}{56} = \frac {40}{56} \)
حال سه کسر مثبت با مخرج برابر داریم، کسری بزرگتر است که صورت بزرگتری داشته باشد:
\( \LARGE \frac {112}{56} \) , \( \LARGE \frac {105}{56} \) , \( \LARGE \frac {40}{56} \)
یعنی:
\( \LARGE 2 \) , \( \LARGE 1\frac {7}{8} \) , \( \LARGE \frac{5}{7} \)
(مقایسه اعداد منفی):
در مورد اعداد منفی نیز ابتدا آن‌ها را بصورت کسری مینویسیم (توجه کنید که طبق تعریف اعداد گویا هر عدد اعشاری، یک عدد کسری با مخرج 10 است):
\( \LARGE-\frac {31}{3} \)
\( \LARGE -3/1 = -3\frac {1}{10} \)
\( \LARGE = -\frac{(3×10)+1}{10} = -\frac{31}{10} \)
مشاهده میکنیم که صورت هر دو کسر منفی برابرند، پس کسری بزرگتر است که مخرج بزرگتر داشته باشد (یعنی \( \Large -\frac{31}{10} \)).
بنابراین این اعداد را به ترتیب از کوچک به بزرگ (از چپ به راست) مینویسیم:
\( \LARGE 2 \) , \( \LARGE 1\frac {7}{8} \) , \( \LARGE \frac{5}{7} \) , \( \Large -3/1 \) , \( \LARGE -\frac {31}{3} \)
نوشتن چند عدد بین دو عدد گویا
برای نوشتن چند عدد گویا بین دو عدد گویای داده شده، دو روش زیر را به کار ببرید:
- صورت‌ها را با هم و مخرجها را با هم جمع میکنیم؛
- ابتدا مخرج مشترک گرفته و سپس صورت و مخرج را در یک واحد بیشتر از تعداد خواسته شده ضرب میکنیم.
مثال 6: بین دو عدد \( \Large \frac {2}{3} \) و \( \Large \frac {1}{5} \) دو عدد گویا بنویسید.
حل 6:
(روش اول): صورت‌ها را با هم و مخرجها را با هم جمع میکنیم، اولین عدد بدست می‌آید، برای بدست آمدن عدد دوم باز هم صورت و مخرج دو طرف را با هم جمع میکنیم:
(روش دوم): مخرج مشترک می‌گیریم (15)؛ بنابراین این دو کسر به ترتیب برابرند با:
\( \LARGE \frac {2×5}{15} = \frac {10}{15} \)
\( \LARGE \frac {1×3}{15} = \frac {3}{15} \)
چون دو عدد از ما خواسته شده، مخرج کسر (15) را در (3) ضرب میکنیم:
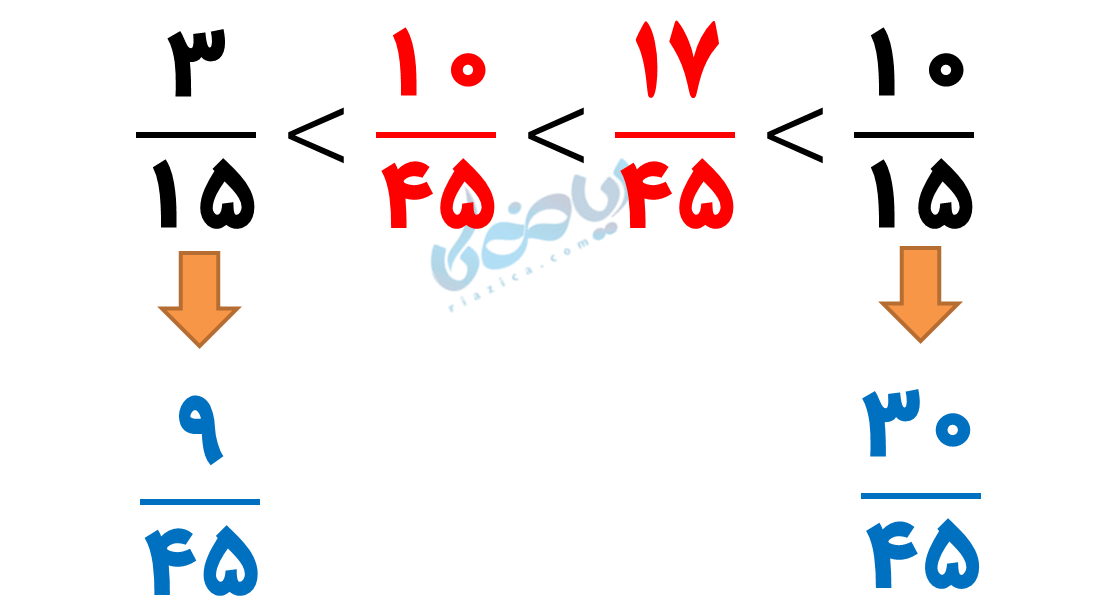
بدست آوردن مجهول از تساوی دو کسر
در تساوی دو کسر، اگر یک مجهول در صورت یا مخرج داشته باشیم، می‌توان با «طرفین وسطین» آن را محاسبه نمود. برای این کار مطابق شکل زیر بصورت ضربدری اعداد را در هم ضرب میکنیم. سپس تبدیل به حل معادله درجه اول میشود.
برای فهم بهتر این موضوع، به مثال زیر توجه کنید:
\( \Large 5×x = 25×3 \)
\( \Large 5x = 75 \)
\( \LARGE x = \frac {75}{5} = 15 \)
در ادامه حتما پست چهار عمل اصلی اعداد گویا رومطالعه کن
زنگ آخر کلاس تعریف اعداد گویا
در این درس ضمن تعریف اعداد گویا به بررسی ارتباط مجموعه اعداد مختلف با هم پرداختیم و مسائل مختلفی در مورد عددهای گویا از جمله روش ساده کردن کسر، نوشتن چند عدد گویا بین دو عدد گویا و مقایسه اعداد گویا با هم را یاد گرفتیم. تعداد زیاد مثال‌های این درس، تمرین مناسبی برای عبور از قله عددهای گویاست.
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاه‌ها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.
ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی هشتم به شما پیشنهاد می‌دهیم:
- زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعی‌ها!
- اعداد صحیح ↔️➖➕– نمایش روی محور مختصات
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعی‌ها!
- تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
- عدد اول ریاضی هشتم 1️⃣👨🎓 – کامل‌ترین آموزشی که لازم داشتید.
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- خط و دایره : از سیر ➖ تا پیاز 🔴
- خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خطها در چهارراه زاویه!
- چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!
- ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
- فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارتهای جبری استفاده کن!
- حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
- بردار و مختصات ریاضی هشتم ➡️⬅️ – جهتدار و کامل!
- بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
- شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
- مثلث های هم نهشت 🌷🔺 گل سرسبد شکلهای همنهشت!
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
- همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد میگیرید
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!
با عرض ادب وخسته نباشید — قوانین اصلی اعداد گویا بیان نمایید؟
سلام و عرض ادب
سوالتون رو واضح تر بیان کنید چون اعداد که قانون ندارن.
ین دوعدد رادیکال ۳ ومنفی رادیکال سه بیشمار عدد صحیح وجود دارد
ایا این استدلال درسته؟!
با سلام وعرض اذب
خیر فقط سه عدد صحیح قرار دارد بیشمار عدد حقیقی بین این دو عدد وجود دارد نه صحیح
سلام ، اعدادی که در زیر رادیکال قرار دارند ؛ گویا هستند؟
در صورتی که عدد را نتوانیم به صورت یک عدد صحیح بنویسیم . مثلا ۲ زیر رادیکال قرار داشته باشه
با سلام وعرض ادب
تمام اعدادی که جذر کامل ندارند گنگ هستن نه گویا
نماد ریاضی زیر مجموعه اعداد گویا اسمشون به فارسی چیه
سلام دوست عزیز نماد اعدد گویا Q میشه ولی زیر مجموعه های آن بی نهایت هستند که هر کدوم روبا هر حرفی میتوانیم نامگذاری کنیم
نماد ریاضی زیر مجموعه های اعداد گویا اسمشون چیه
مثلا:N=…
سلام پاسخ داده شد
N اعداد طبیعی (از یک شروع میشه تا بینهایت)
W اعداد حسابی ( از صفر شروع میشه تا بینهابت)
Z اعداد صحیح(…،2 ، ۰،1، منفی ۱، منفی ۲،…)
با سلام وعرض ادب
ممنون ازپاسخگویی شما
سلام و وقت بخیر اعداد گویا مساوی چیست؟
مثلا” یک دوم،سه ششم،پنج دهم،اینا اگه ساده بشن همشون میشن ،یک دوم،
آیا به اینها میگن اعداد گویا مساوی؟؟؟؟
با سلام دوست عزیز
بله مثالی که زدید درست علاوه بر اون گاهی یه عدد گویا به شکل اعشاری وهمون عددبه صورت کسری هم نوشته میشه اونها هم مساوی هستن مثل 0/5 و یک دوم
باسلام,چرا به این اعداد گویا میگوییم؟
و اینکه تفاوت کسر گویا با عبارت گویا چیست؟
با سلام واحترام
چون وقتی به اعداد اعشاری تبدیل میشن یامختوم میشن یعنی اعشارشون تموم میشه یا به تناوب (تکرار)میرسن ولی اعداد گنگ اعشارشون نه تموم میشه نه تکرار
عبارت گویا صورت ومخرجش چند جمله ای یا همون عبارت جبری هست
با سلام خسته نباشید در مورد ساده کردن کسر گویا توضیح واضح تری دهید
با تشکر
با سلام وعرض ادب
پستهای دیگه ما رو در مورد اعدا گویا مطالعه کنید
سلام چه اعدادي گويا نيست ؟
با سلام وعرض ادب
اعداد گنگ یا همون اصم که شامل تمام اعدادی که ریشه کامل ندارن و به عبارت جامع تر اعدادی که نشه اونها رو به شکل کسری نوشت
سلام
آیاهرعددگویا یک‌عددصحیح‌هم‌است؟
با سلام واحترام
خیر هر عدد صحیح یک عدد گویاست نه برعکس چون میشه یه عدد صحیح رو به شکل کسری نوشت با مخرج یک
سلام هر کسری که مخرج و صورتش عدد صحیح باشه گویاست؟
و فرقی نداره که صورتش چ عددی باشه
و مخرجش چه عددی باشه؟ و باید صورت مخرجش فقط صحیح باشه که گویا به حساب بیاد؟
با عرض سلام وادب
بله فقط مخرج صفر نباید باشه
ببخشید من درس گویا رو خوب متوجه نشدم به روش واضع تر توضیح دهید با مثال …………ممنونم
با سلام
هر عددی که بشه اون رو به شکل کسری نوشت میشه عدد گویا مثلا اعداد اعشاری حتی اعداد طبیعی وصحیح
بله
با سلام و خسته نباشید آیا عدد ۰ در صورت و -۸ در مخرج یعنی عدد صفر منفی هشتم گویا است
با سلام وادب
این کسر مساوی صفر است وگویاست هر کسری که صورتش صفر باشد برابر صفر است
سلام در قسمت نوشتن چند عدد بین دو عدد گویا در روش دوم چطور ۱۰ ۱۵ام و ۱۷ ۱۵ ام بدست اوردید در صورتیکه گفتین بعد هم مخرج کردن صورت و مخرج را در..ضرب کنیم
میشه توضیح بدید اون دو عدد وسط قرمز رنگ چطور بدست اومده؟ممنون
با سلام دوست عزیز
ابتدا مخرجها رو یکی میکنیم بعد چون بین ابنها دوعدد گویای دیگر میخواهد صورت وخرج را در ۳ ضزب میکنیم یعنی یکی بیشتر مثلا اگر چهار عدد میخواست در ۵ ضرب میکردیم سپس اعداد بین شان را مینویسیم
با سلام‌میشه روش دوم اعداد بین دو عدد گویا رو توضیح بدید در مثال اون اعداد قرمز چطور بدست اومدن؟
باسلام عدد11/19(بخوانید یازد به روی نوزده)یک کسرهست ولی گویا نیست چون از انجام تقسیم دوعدد، به یک عدد مختوم یا متناوب ساده یامرکب نمیرسیم پس تعریف عدد گویا نقض میشه
لطفا اشتباه من رابرطرف نمایید
سلام دوست عزیز
این عدد گویاست چون تعریف عدد گویا را شامل میشود که از تقسیم دو عدد صحیح به وجود می آید وحتما متناوب ساده هست چون مخرجش عدد اول غیر از ۲ و۵ هست در این کسر بعد از شانزده رقم به تناوب میرسیم
تعریف عدد گنگ این است که عدد اعشاری که نتوان به صورت کسر نوشت واعشار آن نه مختوم هست ونه متناوب مثل رادیکال دو
مشکل شمادر تعریف هست