آموزش ریاضی پایه هشتم
بردار و مختصات ریاضی هشتم ➡️⬅️ – جهت‌دار و کامل!
شهریور
بردار، بهشت ریاضیاته! هر جای علوم (فیزیک مکانیک) که نگاه کنی یه اثر ازش می‌بینی، حتی واسه پرتاب موشک! در درسنامه جامع و بسیار مهم بردار و مختصات ریاضی هشتم از مجموعه آموزش ریاضی پایه هشتم ، این موارد آموزش داده خواهد شد:
- یادآوری بردارها و تعاریف اولیه
- جمع بردارها (بردار برایند)
- تجزیه بردار
- ضرب عدد در بردار
مثال‌های زیاد و متنوعی در این درس برای شما در نظر گرفته‌ایم. حتماً با خواندن آن‌ها این مبحث مهم را مثل آب خوردن یاد می‌گیرید.
یادآوری بردارها؛ مقدمه درس بردار و مختصات ریاضی هشتم
در ریاضیات پایه هفتم (فصل 8) و درسنامه بردارهای مساوی وقرینه با بردارها آشنا شدیم. اگر فراموش کردید جای نگرانی نیست! به چند تعریف زیر توجه کنید تا بعد از آن به اصل درس بردار و مختصات ریاضی هشتم بپردازیم:
تعریف بردار
به هر پاره‌خط جهت دار، یک بردار گفته می‌شود. بردار یک نقطه شروع (مثلاً \( \Large A \)) و یک نقطه پایان (مثلاً \( \Large B \)) دارد. معمولاً با دو حرف بزرگ انگلیسی (شامل نقاط ابتدا و انتها) و یا یک حرف کوچک انگلیسی با یک پیکان بالای سر آن نشان داده می‌شود.
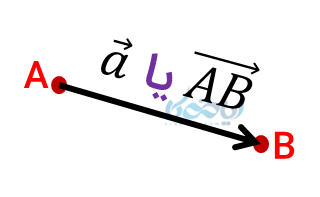
دو بردار مساوی
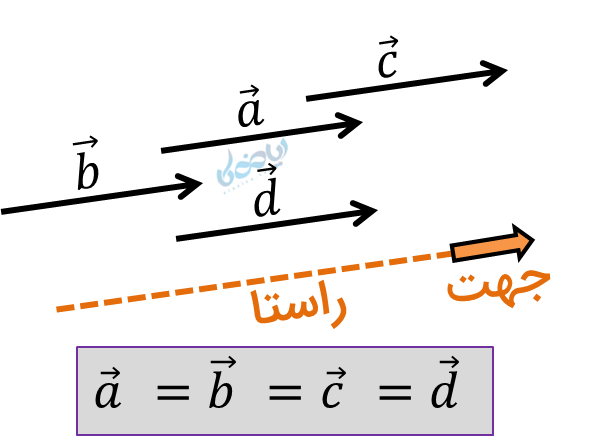
دو بردار با شرایط زیر بردارهای مساوی گفته می‌شوند:
- هم‌اندازه،
- هم‌راستا (موازی)
- هم‌جهت
مانند بردارهای \( \Large \overrightarrow{a}\)، \( \Large \overrightarrow{b}\)، \( \Large \overrightarrow{c}\) و \( \Large \overrightarrow{d}\).
دو بردار قرینه
دو بردار با شرایط زیر بردارهای قرینه گفته می‌شوند:
- هم اندازه،
- هم راستا (موازی)
- خلاف جهت هم
در شکل زیر، بردارهای \( \Large \overrightarrow{AB}\) و \( \Large \overrightarrow{CD}\) قرینه‌اند.
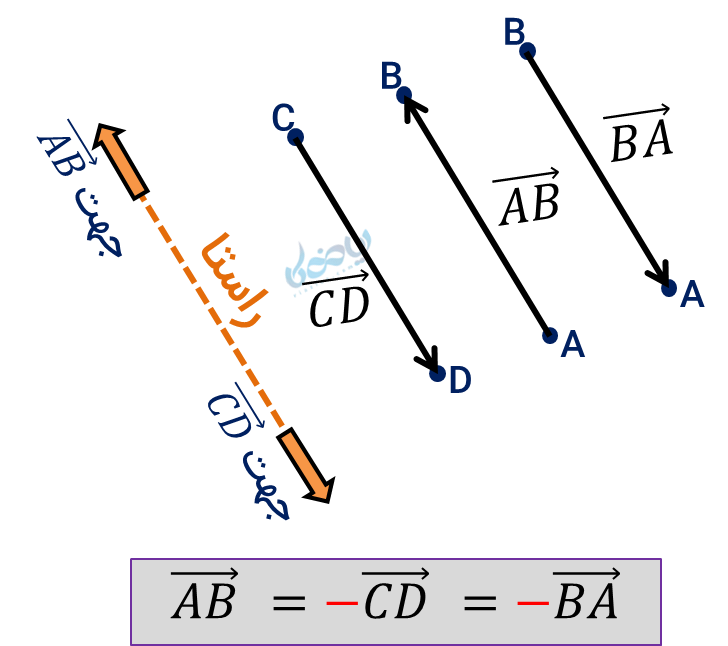
نکته: اگر ابتدا و انتهای بردار را جابجا کنیم، برداری قرینه بردار اول بدست می‌آید. (مانند بردار \( \Large \overrightarrow{BA}\)).
مختصات بردار
خب! از اسم درس هم مشخصه: بردار و مختصات ریاضی هشتم – پس بیایید مختصات بردارها را هم یاد بگیریم. برای بدست آوردن مختصات بردار کافی است مختصات نقطه ابتدایی را از مختصات نقطه انتهایی بردار تفریق کنیم؛ یعنی:
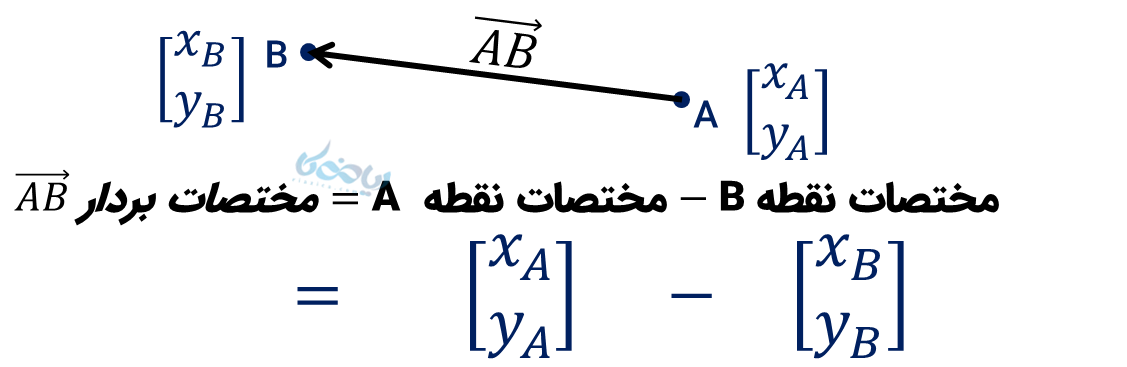
مثال 1: در شکل زیر برای بردار \( \Large \overrightarrow{f}\) یک بردار مساوی و یک بردار قرینه رسم کنید و مختصات آن را بدست آورید.
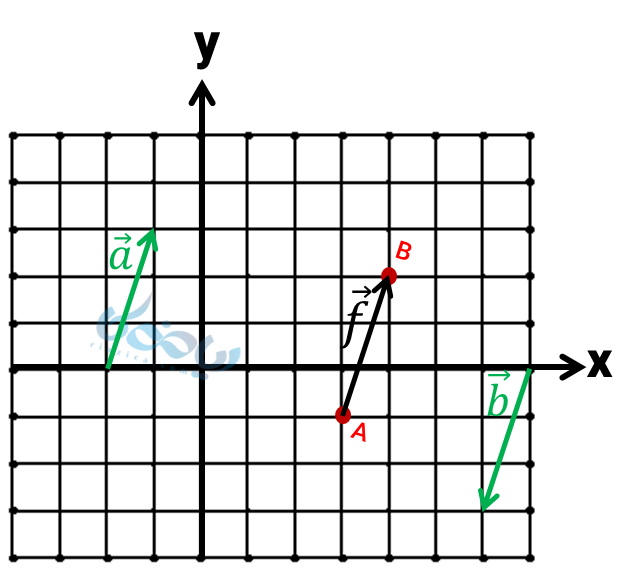
حل 1:
نقاط ابتدا و انتهای بردار \( \Large \overrightarrow{f}\) را به ترتیب \( \Large A \) و \( \Large B \) نام‌گذاری کرده‌ایم. برای بدست آوردن مختصات بردار، مختصات \( \Large A \) را از مختصات \( \Large B \) کم می‌کنیم:
\( \Large {\rm{A = }}\left[ \begin{array}{l}{\rm{3}}\\{\rm{ – 1}}\end{array} \right] \)
\( \Large {\rm{B = }}\left[ \begin{array}{l}{\rm{4}}\\{\rm{2}}\end{array} \right] \)
\( \Large \overrightarrow{AB} = \left[ \begin{array}{l}{\rm{4}}\\{\rm{2}}\end{array} \right] – \left[ \begin{array}{l}{\rm{3}}\\{\rm{ -1}}\end{array} \right] = \left[ \begin{array}{l}{\rm{1}}\\{\rm{3}}\end{array} \right] \)
این مختصات نشان‌دهنده همان چیزی است که در شکل هم دیدیم؛ یعنی بردار \( \Large \overrightarrow{f}\) ، حرکت یک واحد به سمت راست و سه واحد به سمت بالا را نشان می‌دهد.
برای رسم بردارهای مساوی و قرینه این بردار، مطابق تعاریف بالا عمل می‌کنیم؛ یعنی برداری هم اندازه و هم راستا با بردار \( \Large \overrightarrow{f}\) رسم می‌کنیم. (برای بردار مساوی هم جهت و برای بردار قرینه خلاف جهت آن).
بنابراین بردار \( \Large \overrightarrow{a}\) را یک واحد به راست و سه واحد بالا رسم کرده‌ایم (مساوی). بردار \( \Large \overrightarrow{b}\) را یک واحد به چپ و سه واحد پایین رسم کرده‌ایم (قرینه).
جمع بردارها؛ پادشاه درس بردار و مختصات ریاضی هشتم
در مبحث بردار و مختصات ریاضی هشتم برای جمع بردارها و بدست آوردن بردار برایند (بردار حاصل جمع) دو روش آموزش داده می‌شود:
- روش مثلثی
- روش متوازی الاضلاع
روش مثلثی
در این روش، دو بردار را پشت سر هم رسم می‌کنیم؛ به صورتی که ابتدای بردار دوم (\( \Large \overrightarrow{b}\))، انتهای بردار اول (\( \Large \overrightarrow{a}\)) باشد. سپس از ابتدای بردار اول به انتهای بردار اول رسم می‌کنیم. بردار بدست آمده همان بردار برایند خواهد بود.
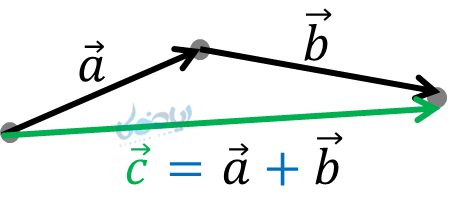
نکته: از روش مثلثی می‌توان برای جمع هر تعداد بردار (بدست آوردن برایند هر تعداد بردار) استفاده کرد؛ کافی است همه بردارها را پشت سر هم رسم کرده و از ابتدای بردار اول به انتهای بردار آخر وصل کنیم. مانند بردار برایند \( \Large \overrightarrow{g}\) در شکل زیر:
مثال 2: تعدادی بچه مشغول بازی هستند و جعبه نشان داده شده را هُل می‌دهند. در نهایت این جعبه به کدام سمت حرکت خواهد کرد؟
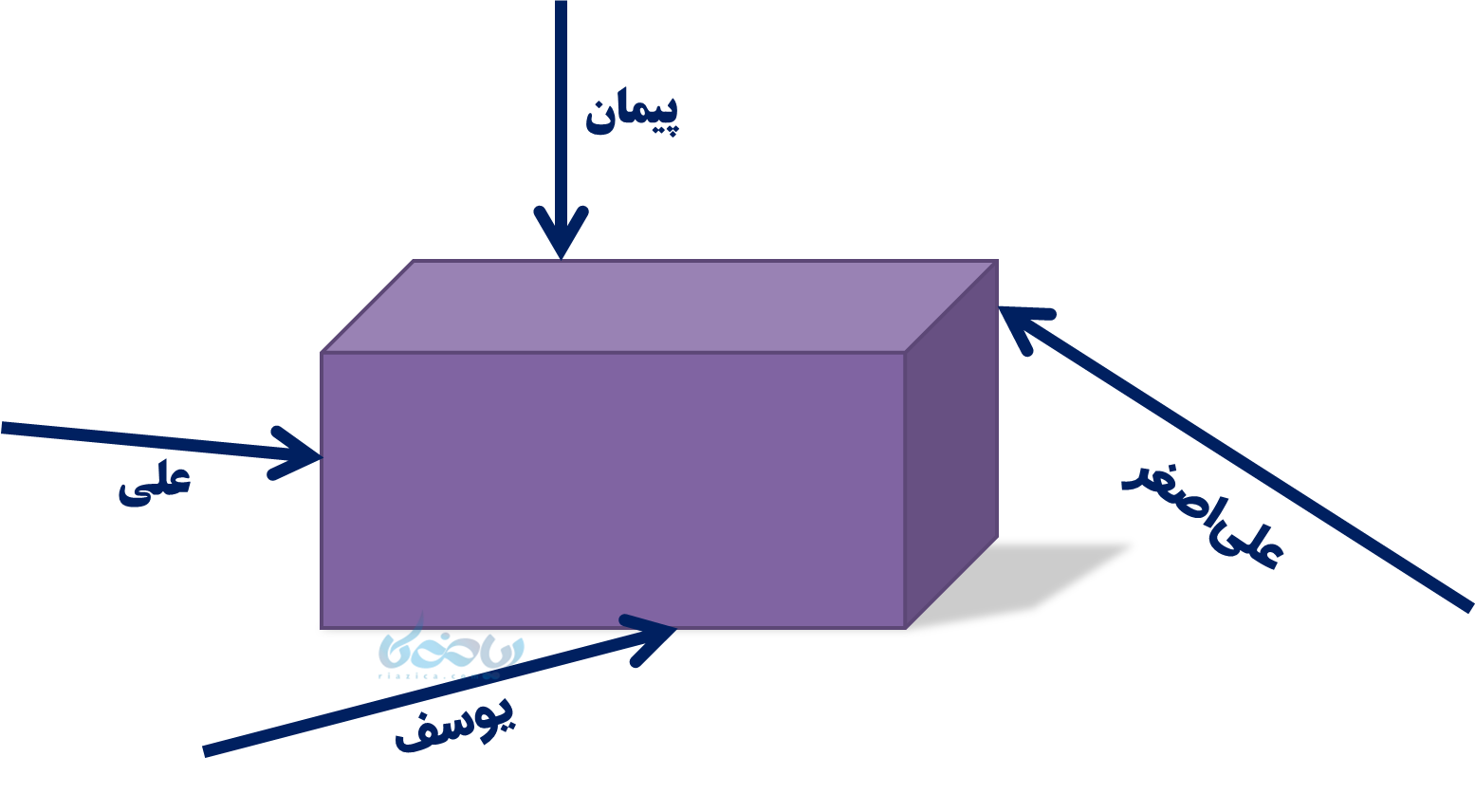
حل 2:
خب این هم یکی از کاربردهای برایند بردارها! برای این که بدانیم جعبه به کدام سمت حرکت می‌کند، بردار برایند را بدست می‌آوریم. به روش مثلثی، همه بردارها را پشت سر هم رسم کرده و سپس از ابتدای بردار اول به انتهای بردار آخر می‌کشیم.
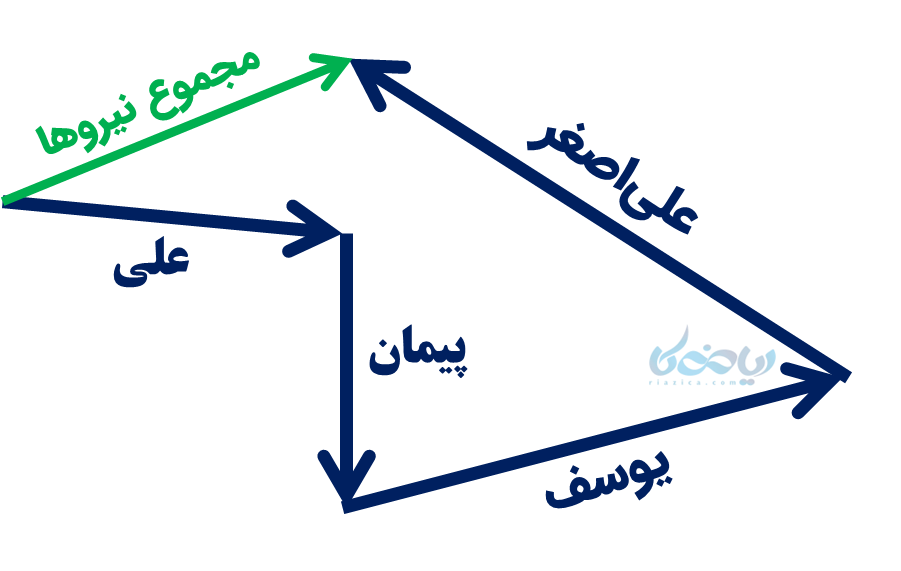
با توجه به نمودار برایند نیروها، این جعبه در نهایت به طرف بالا سمت راست حرکت خواهد کرد.
روش متوازی الاضلاع
در این روش، دو بردار را از یک نقطه رسم می‌کنیم؛ سپس از انتهای یکی از بردارها، برداری مساوی بردار دیگر رسم می‌کنیم (تبدیل به روش مثلثی می‌شود!). با رسم از ابتدای نقطه اول دو بردار تا انتهای بردار جدید بردار برایند بدست خواهد آمد.
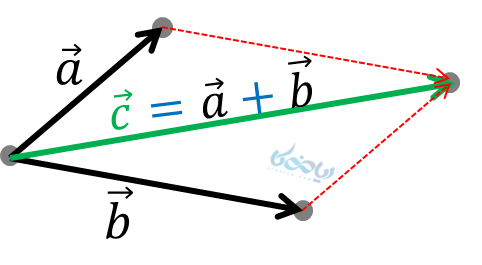
همان‌طور که در شکل مشاهده می‌کنید، هم می‌توان از انتهای بردار \( \Large \overrightarrow{a}\) ، برداری مساوی \( \Large \overrightarrow{b}\) رسم کرد و هم بالعکس. با رسم هر دو شکل متوازی الاضلاع بدست آمد! حالا متوجه شدید چرا بهش میگن روش متوازی‌الاضلاع؟
مثال 3: بردارهای \( \Large \left[ {\begin{array}{*{20}{l}}{\rm{2}}\\{\rm{3}}\end{array}} \right] \) و \( \Large \left[ {\begin{array}{*{20}{l}}{{\rm{ – 2}}}\\{\rm{1}}\end{array}} \right] \) را از مبدأ مختصات رسم کرده و سپس برایند آن‌ها را بدست آورید.
حل 3:
از مبدأ ابتدا بردار اول را رسم می‌کنیم: انتهای بردار 2 واحد به راست و 3 واحد به بالا است، سپس برای رسم بردار دوم، 2 واحد به سمت چپ و 1 واحد به سمت بالا حرکت می‌کنیم.
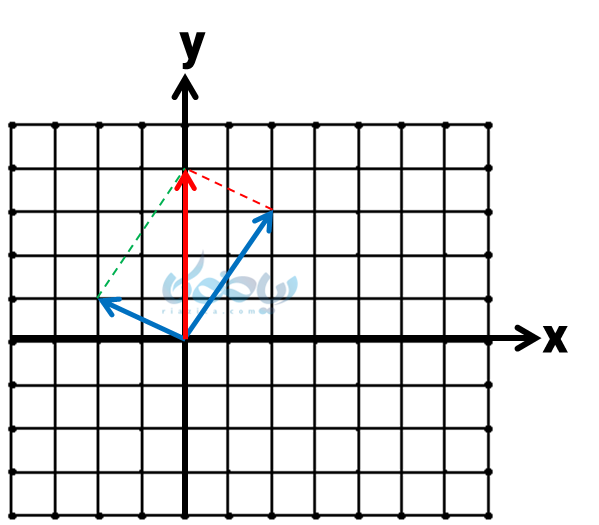
می‌بینیم که ابتدای دو بردار یک نقطه است، بنابراین بهتر است از روش متوازی الاضلاع استفاده کنیم. از انتهای بردار اول، مساوی بردار دوم (قرمز رنگ) یا از انتهای بردار اول، مساوی بردار دوم (سبز رنگ) رسم می‌کنیم. ابتدا را به انتها وصل می‌کنیم. بردار آبی رنگ همان بردار برایند است.
بردار صفر
بردار صفر به صورت \( \Large \overrightarrow{o}\) نشان داده می‌شود. مختصات آن \( \Large \left[ \begin{array}{l}{\rm{0}}\\{\rm{0}}\end{array} \right] \) است.
نکته: جمع دو بردار قرینه برابر با بردار صفر است.
چون می‌توان قرینه بردار \( \Large \overrightarrow{a}\) را بصورت بردار \( \Large – \overrightarrow{a}\) نوشت. حاصل جمع آن‌ها بدین صورت خواهد بود:
\( \Large \overrightarrow{a} + (- \overrightarrow{a}) = \overrightarrow{o} \)
مثال 4: جمع بردارهای نشان داده شده را بدست آورید.
حل 4:
در درس بردار و مختصات ریاضی هشتم با دو روش آشنا شدیم. حالا از کدام روش استفاده کنیم؟
خب! بردارها پشت سر هم رسم شده‌اند، پس از روش مثلثی باید از ابتدای بردار اول به انتهای بردار آخر وصل کنیم، اما مشاهده می‌شود که ابتدای بردار اول دقیقاً روی انتهای بردار آخر افتاده است. پس برایند این بردارها برابر با بردار صفر خواهد بود.
تساوی برداری و تساوی مختصاتی (بردار و مختصات ریاضی هشتم به زبان ریاضی!)
می‌توان جمع بردارها یا هر نوع عمل جبری دیگر روی بردارها (مانند تفریق و …) را به دو صورت نشان داد:
- تساوی برداری: در این حالت، تنها نماد بردارها (مانند \( \Large \overrightarrow{a}\)) نوشته می‌شود.
- تساوی مختصاتی: در این حالت به جای نماد بردارها، مختصات آن‌ها نوشته می‌شود.
در دو رابطه زیر، جمع‌های برداری و مختصاتی نشان داده شده است:
(جمع برداری) \( \Large \overrightarrow{a} + \overrightarrow{b} = \overrightarrow{c} \)
(جمع مختصاتی) \( \Large \left[ \begin{array}{l}{{\rm{x}}_{\rm{a}}}\\{{\rm{y}}_{\rm{a}}}\end{array} \right]{\rm{ }} + {\rm{ }}\left[ \begin{array}{l}{{\rm{x}}_{\rm{b}}}\\{{\rm{y}}_{\rm{b}}}\end{array} \right]{\rm{ }} = {\rm{ }}\left[ \begin{array}{l}{{\rm{x}}_{\rm{c}}}\\{{\rm{y}}_{\rm{c}}}\end{array} \right] \)
مثال 5: برای شکل زیر یک جمع برداری و یک جمع مختصاتی بنویسید.
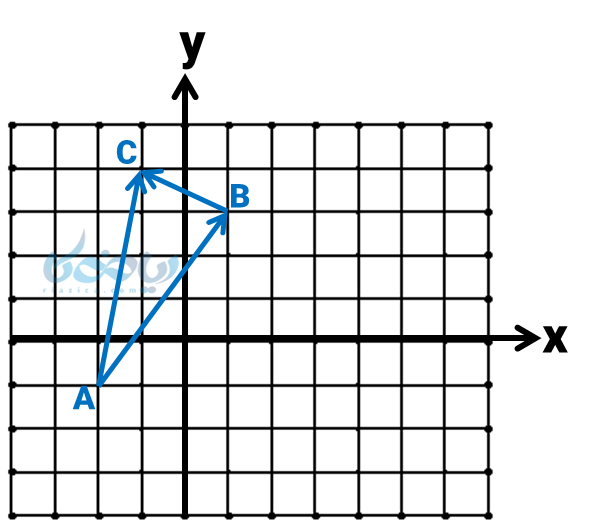
حل 5:
بردارهای \( \Large \overrightarrow{AB}\) و \( \Large \overrightarrow{BC}\) پشت سر هم رسم شده‌اند و بردار برایند آن‌ها یعنی \( \Large \overrightarrow{AC}\) از روش مثلثی بدست آمده است؛ پس جمع برداری آن‌ها بدین صورت خواهد بود:
(جمع برداری) \( \Large \overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC} \)
اگر در این تساوی مختصات بردارها را جای‌گذاری کنیم، به جمع مختصاتی این شکل خواهیم رسید:
(جمع مختصاتی) \( \Large \left[ \begin{array}{l}{\rm{3}}\\{\rm{4}}\end{array} \right]{\rm{ }} + {\rm{ }}\left[ \begin{array}{l}{\rm{ – 2}}\\{\rm{1}}\end{array} \right]{\rm{ }} = {\rm{ }}\left[ \begin{array}{l}{\rm{1}}\\{\rm{5}}\end{array} \right] \)
تجزیه بردار
عمل تجزیه بردار، برعکس عمل بدست آوردن بردار برایند است. اگر بخواهیم برداری را روی دو راستا (محور) تجزیه کنیم بدین روش عمل می‌کنیم.
از انتهای بردار به موازات دو محور خط رسم می‌کنیم؛ نقاطی که این دو خط، محورها یا امتداد آن‌ها را قطع می‌کند، نقاط انتهای بردارها خواهد بود. نقاط ابتدای بردارها، همان نقطه ابتدایی بردار اولیه است. (شبیه برایند گرفتن از روش متوازی‌الاضلاع)
شکل زیر، نحوه تجزیه بردار \( \Large \overrightarrow{a}\) را بر روی دو راستای بنفش رنگ نشان می‌دهد. مشاهده می‌شود که این بردار، به دو بردار \( \Large \overrightarrow{a_1}\) و \( \Large \overrightarrow{a_2}\) تجزیه شده است.
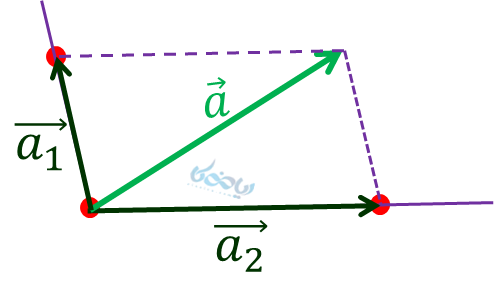
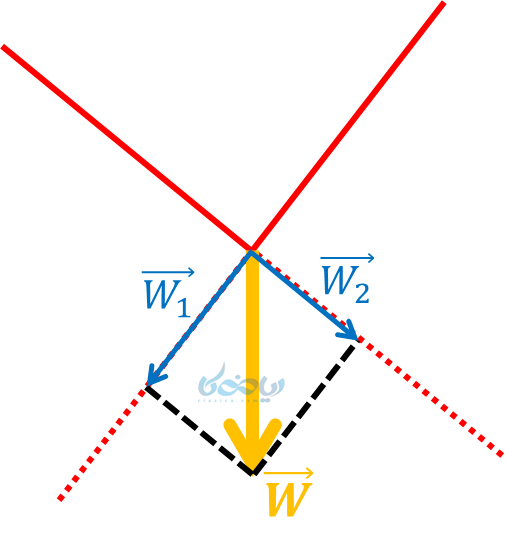
مثال 6: وزن کودکی که روی سرسره در حال بازی است با بردار زرد رنگ \( \Large \overrightarrow{W}\) نشان داده شده است. این بردار را بر روی دو امتداد نشان داده شده تجزیه کنید.
حل 6:
گفتیم که برای تجزیه بردار، باید از انتهای بردار به موازات دو محور خط رسم می‌کنیم. در این مثال، این خطوط محورها را قطع نمی‌کند، اما امتداد آن‌ها (نقطه‌چین) را قطع می‌کند. بنابراین این بردار بصورت زیر تجزیه می‌شود:
ضرب عدد در بردار
در ضرب یک عدد مانند \( \Large k \) در بردار، آن عدد در طول و عرض بردار ضرب می شود. (به زبان ریاضی):
\( \Large {\rm{k}} \times \left[ \begin{array}{l}{\rm{x}}\\{\rm{y}}\end{array} \right] = \left[ \begin{array}{l}{\rm{kx}}\\{\rm{ky}}\end{array} \right] \)
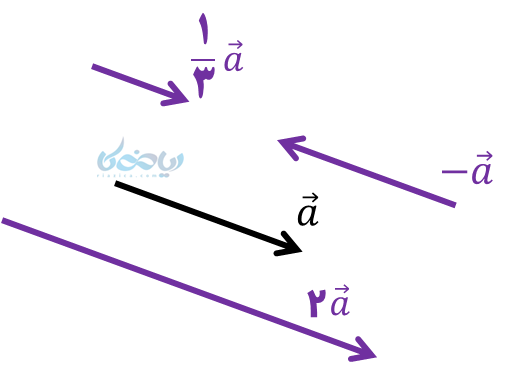
نکته 1: با ضرب عدد در بردار، راستای آن تغییر نمی‌کند؛ اما جهت آن در صورت منفی بودن عدد تغییر می‌کند.
نکته 2: اگر عدد ضرب شده، بزرگتر از 1 باشد، بردار بزرگتر و اگر بین 0 و 1 باشد، بردار کوچکتر می‌شود.
نکته 3: قرینه بردار، یعنی آن بردار در عدد (1-) ضرب شود.
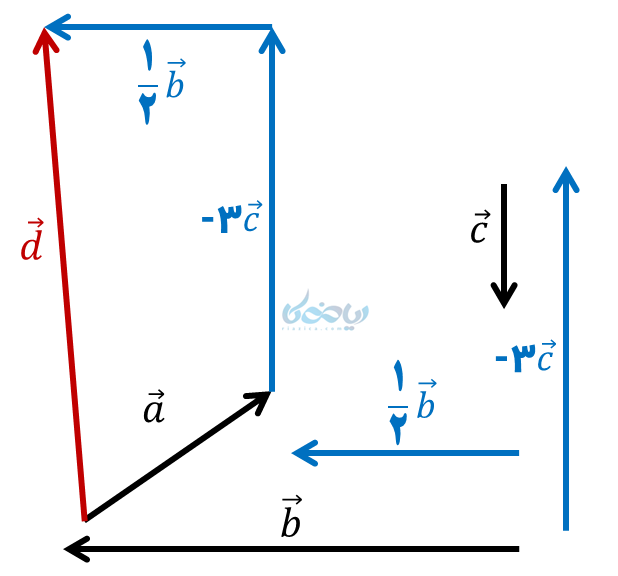
مثال 7 ( مثالی ترکیبی از درس بردار و مختصات ریاضی هشتم ): با توجه به بردارهای \( \Large \overrightarrow{a}\)، \( \Large \overrightarrow{b}\) و \( \Large \overrightarrow{c}\)، بردار \( \Large \overrightarrow{d}\) را رسم نمایید.
\( \Large \overrightarrow{d} = \overrightarrow{a} – 3 \overrightarrow{c} + \frac {1}{2} \overrightarrow{b} \)
حل 7:
می‌توانیم در رابطه بالا، علامت تفریق را تغییر داده و رابطه را بدین صورت بنویسیم:
\( \Large \overrightarrow{d} = \overrightarrow{a} + (-3 \overrightarrow{c}) + \frac {1}{2} \overrightarrow{b}\)
حال ابتدا عددهای قبل از بردارها در آن‌ها ضرب کرده و سپس به روش مثلثی بردار برایند (یعنی \( \Large \overrightarrow{d} \)) را رسم می‌کنیم:
مثال نهایی درس بردار و مختصات ریاضی هشتم
مثال 8: حاصل عبارت‌های زیر را بدست آورید.
الف) \( \Large {\rm{5}}\left[ \begin{array}{l}{\rm{3}}\\{\rm{ – 1}}\end{array} \right] = {\rm{?}} \)
ب) \( \Large {\rm{2}}\left[ \begin{array}{l}{\rm{ – 4}}\\{\rm{ – 1}}\end{array} \right] – {\rm{3}}\left[ \begin{array}{l}{\rm{ – 3}}\\{\rm{4}}\end{array} \right]{\rm{ = ?}} \)
حل 8:
الف) \( \Large {\rm{5}}\left[ {\begin{array}{*{20}{l}}{\rm{3}}\\{{\rm{ – 1}}}\end{array}} \right] = \left[ {\begin{array}{*{20}{l}}{{\rm{15}}}\\{{\rm{ – 5}}}\end{array}} \right] \)
ب) \( \Large {\rm{2}}\left[ \begin{array}{l}{\rm{ – 4}}\\{\rm{ – 1}}\end{array} \right] – {\rm{3}}\left[ \begin{array}{l}{\rm{ – 3}}\\{\rm{4}}\end{array} \right]{\rm{ }} \)
\( \Large = {\rm{2}}\left[ \begin{array}{l}{\rm{ – 4}}\\{\rm{ – 1}}\end{array} \right] + {\rm{( – 3)}}\left[ \begin{array}{l}{\rm{ – 3}}\\{\rm{4}}\end{array} \right]{\rm{ }} \)
\( \Large {\rm{ = }}\left[ \begin{array}{l}{\rm{ – 8}}\\{\rm{ – 2}}\end{array} \right]{\rm{ + }}\left[ \begin{array}{l}{\rm{9}}\\{\rm{ – 12}}\end{array} \right]{\rm{ }} \)
\( \Large {\rm{ = }}\left[ \begin{array}{l}{\rm{ – 8 + 9}}\\{\rm{ – 2 – 12}}\end{array} \right] = \left[ \begin{array}{l}{\rm{1}}\\{\rm{ – 14}}\end{array} \right] \)
زنگ آخر کلاس بردار و مختصات ریاضی هشتم
بردارها را در پایه‌های مختلف دیده‌ایم و خواهیم دید، اما قطعاً بردار و مختصات ریاضی هشتم یکی از کاربردی‌ترین آن‌هاست! در این درسنامه به یادگیری جمع بردارها و دو روش رسم بردار برایند، تجزیه بردار و ضرب عدد در بردار پرداختیم و با حل کلی مثال کاربردی خواهیم توانست با بردارهای مختلف در فیزیک و زندگی کار کنیم.
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاه‌ها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.
ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی هشتم به شما پیشنهاد می‌دهیم:
- زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعیها!
- اعداد صحیح ↔️➖➕– نمایش روی محور مختصات
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعیها!
- تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
- عدد اول ریاضی هشتم 1️⃣👨🎓 – کاملترین آموزشی که لازم داشتید.
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- خط و دایره : از سیر ➖ تا پیاز 🔴
- خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خطها در چهارراه زاویه!
- چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!
- ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
- فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارت‌های جبری استفاده کن!
- حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
- بردار و مختصات ریاضی هشتم ➡️⬅️ – جهت‌دار و کامل!
- بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
- شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
- مثلث های هم نهشت 🌷🔺 گل سرسبد شکلهای همنهشت!
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
- همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد می‌گیرید
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!
خیلی عالییییییییی
ممنون واقعا خیلی خوب بود
سلام و عرض ادب
ممنون از انرژیتون
موفق باشید.
خیلی عالی بود ممنون
سلام و عرض ادب
ممنون از انرژی و پیام پرمهرتون.
موفق باشید
عالی بود
سلام دوست عزیز
ممنون از توجهی که داشتید.
موفق باشید.
خوشمل توضیح دادید 👏
عااااااااااااااااااااااالیییییییییییییییییییییی بود. ممنون از مطالب خیلی خوبتون
سلام و عرض ادب
ممنون از انرژی و توجهی که داشتید.
موفق باشید.
ممنون عالی بود
سلام دوست عزیز
ممنون از انرژی که دادید.
موفق باشید.
سلام.
عالی بود
خیلی ساده و روان توضیح داده شد
موفق باشید.
سلام و عرض ادب
ممنون از توجهی که داشتید.
موفق باشید.
عالیییییی
سلام دوست عزیز ممنون از توجه شما
عالی
سلام و عرض ادب
ممنون از انرژیتون
موفق باشید
خوب بود
سلام دوست عزیز
ممنون از محتب شما
به دردم نخورد?
با عرض سلام
متاسفیم اما فک کنم با دقت بخونید به دردتون بخوره
ممنون عالير بود
عالي بود
برچی
سلام خیلی ممنونم از مطالب خوبتون ، عالی بودن
سلام و عرض ادب
ممنون از انرژی و پیام پرمهرتون.
موفق باشید
سلام خیلی ممنون ??????
سلام و عرض ادب
ممنون از انرژی و پیام پرمهرتون.
موفق باشید
سلام واقعا ممنون از مطالب بسیار عالی و مفیدتون من فردا امتحان همین فصل رو دارم واقعا یاد گرفتم ببخشید یک سوال معادله مختصات رو توضیح ندادین؟؟
سلام و عرض ادب
ممنون از توجه شما و خوشحالیم که این مطلب را فراگرفته اید.
برای فهمیدن معادله مختصات به لینک زیر بروید:
https://riazica.com/coordinate-unit-vectors/
موفق باشید.
من نکات مهم میخواستم نداشت
سلام دوست عزیز منظورتون از نکات مهم چی هست؟
خیلی خوب بودد ممنونننن واقعا به دردم خورد ??
با سلام ووقت به خیر
خوشحالیم که براتون مفید واقع شده
پیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
ینی الان منف پشت مختصات رو در مختصات اثر نمیدیم؟
با سلام دوست عزیز
چرا اثر میدیم اگه به مثال ۸ هم دقت کنید میبینید اثر داده شده
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام وقت بخیر
آیا در محور مختصاتی که کشیدین واحد j رو روی محور افقی و واحد i رو روی محور عمودی در نظر بگیریم اشتباهه؟
با سلام واحترام
بله قرارداد به صورتی که گفتیم میباشد
بله
خیلیی خوب بود دمتون گرم (-:
با سلام وعرض ادب
خدا رو شک که استفاده بردید
خیلیییییی عالی و کامل توضیح داده بودید
ممــنون ازتون??
با سلام وادب
ممنون از نظر لطف شما
عالی فقط فصل بندی میکردین بهتربود
با سلام
ممنون از پیشنهاد شما
سلام عالللیییییییییی بود
خیلی عالی بود ممنونم ازشما ❤
من یک سوال داشتم آیا دوبردار هم جهت قطعا هم راستا هستند؟
خیر. ولی اگر اون دو بردار مساوی باشن، میتونیم بگیم که هم راستا و هم جهت هستند
سلام ممنون من برا یاد دادن به پسرم استفاده کردم خیلی عالی بود.
با سلام وادب
خدا رو شکر که مفید بوده
اخر من به جوابم نریسیدم عدد نمیخاستم تعرف میخا مثال تعری یا مفهوم بردار برایند را بگویید که میشه حاصل جمع دو بردار حالا تعریف بردار واحد چی میشه
سلام میشه تعریف بردار واحد رو بیگین مثال و عدد نمیخام تعریف یا مفهومشو میخام
مفید و مختصر
عالی بود ممنون
با سلام ودرود
ممنون از نگاه شما
با تهیه پکیج آموزش ریاضی هشتم این پایه رو فول یاد بگیرید
معلم ما میگه که مختصاتی که نوشته شده صفر داشته باشن یه اسم دیگه دارن
با سلام وادب
چه اسمی؟
سلام خیلی ممنون دستتون درد نکند
سلام خیلی ممنون دستتون درد نکند
خوشمل توضیح دادید 👏
دوست داشتم توضیح تونو 👏