آموزش ریاضی پایه نهم
ریشه گیری ریاضی نهم 3️⃣💫 – ریشه سوم اعداد پیدا کن!
دی
در درسنامۀ ریشه گیری ریاضی نهم به بررسی ریشۀ دوم و سوم اعداد خواهیم پرداخت. همچنین، خواهیم دید روابطی که برای ضرب و تقسیم رادیکالها در سال گذشته خواندید، برای ریشۀ سوم اعداد نیز برقرار است. پیشنهاد می‌کنیم قبل از مطالعۀ این درسنامه، درسنامۀ خواص ضرب و تقسیم رادیکالها را مرور کنید. در نگارش این درسنامه سعی کردیم تا با حل مثال‌های مختلف، در درک بهتر مبحث ریشه گیری ریاضی نهم به شما کمک کنیم. با ما تا انتها همراه باشید.
ریشۀ دوم
اگر \(\Large a\) یک عدد حقیقی مثبت باشد، به \(\Large \sqrt{a}\) و \(\Large -\sqrt{a}\) ریشه‌های دوم \(\Large a\) می‌گوییم. در واقع اگر ریشه‌های دوم یک عدد حقیقی مثبت را به توان دوم برسانیم، خود عدد به دست می‌آید. صفر تنها یک ریشۀ دوم دارد که خود صفر است. اگر \(\Large a\) عددی منفی باشد، ریشۀ دوم ندارد، زیرا \(\Large \sqrt{a}\) و \(\Large -\sqrt{a}\) در اعداد حقیقی تعریف نشده‌اند.
برای علاقه‌مندان: ریشۀ دوم یک عدد منفی در اعداد حقیقی وجود ندارد. اما در اعداد مختلط، ریشۀ دوم اعداد منفی نیز تعریف شده است. اگرچه این مبحث خارج از مباحث دبیرستان است اما اگر علاقه دارید می‌توانید در مورد آن مطالعه کنید.
به مثال بعدی از درسنامۀ ریشه گیری ریاضی نهم توجه کنید.
مثال از محاسبۀ ریشۀ دوم
مثال 1: ریشه‌های دوم عدد \(\Large 6\) را در صورت وجود به دست آورید.
حل: اگر \(\Large +\sqrt{6}\) و \(\Large -\sqrt{6}\) را به توان دو برسانیم، عدد \(\Large 6\) به دست می‌آید. بنابراین \(\Large +\sqrt{6}\) و \(\Large -\sqrt{6}\) ریشه‌های دوم عدد \(\Large 6\) هستند.
مثال 2: ریشه‌های دوم عدد \(\Large \frac{16}{25}\) را در صورت وجود به دست آورید.
حل: مطابق با توضیحی که دادیم، عدد \(\Large \frac{16}{25}\) دارای دو ریشۀ دوم زیر است:
\(\LARGE +\sqrt{\frac{16}{25}}=\frac{4}{5}\)
\(\LARGE -\sqrt{\frac{16}{25}}=-\frac{4}{5}\)
به قسمت بعدی از درسنامۀ ریشه گیری ریاضی نهم توجه کنید.
ارتباط ریشۀ دوم و قدر مطلق
در درسنامۀ قدر مطلق ریاضی نهم دیدیم که برای هر عدد حقیقی دلخواه \(\Large a\)، ریشۀ دوم \(\Large a^2\) برابر است با \(\Large |a|\). یعنی داریم
\(\LARGE \sqrt{a^2}=|a|\)
با یادآوری این نکته، به حل دو مثال بعدی از درسنامۀ ریشه گیری ریاضی نهم می‌پردازیم.
مثال از ارتباط ریشۀ دوم و قدر مطلق
مثال 3: حاصل \(\Large \sqrt{(1-\sqrt{3})^2}\) را به دست آورید.
حل: با توجه به نکته‌ای که گفتیم، حاصل \(\Large \sqrt{(1-\sqrt{3})^2}\) برابر با \(\Large|1-\sqrt{3}|\) است. از آنجاییکه \(\Large \sqrt{3}\) بزرگتر از \(\Large 1\) است، حاصل \(\Large 1-\sqrt{3}\) منفی است. در نتیجه داریم:
\(\LARGE \sqrt{(1-\sqrt{3})^2}=|1-\sqrt{3}|\)
\(\LARGE =\sqrt{3}-1\)
به مثال بعدی از درسنامۀ ریشه گیری ریاضی نهم توجه کنید.
مثال 4: اگر \(\Large a\) منفی و \(\Large b\) مثبت باشد، عبارت \(\Large \sqrt{a^2}+\sqrt{b^2}\) را ساده کنید.
حل: همان طور که گفتیم، حاصل \(\Large \sqrt{a^2}\) برابر با \(\Large |a|\) و حاصل \(\Large \sqrt{b^2}\) برابر با \(\Large |b|\) است. یعنی داریم:
\(\LARGE \sqrt{a^2}+\sqrt{b^2}=|a|+|b|\)
از طرفی چون \(\Large a\) منفی است، \(\Large |a|\) برابر است با \(\Large -a\). همچنین، چون \(\Large b\) مثبت است، \(\Large |b|\) برابر است با \(\Large b\). بنابراین داریم:
\(\LARGE \sqrt{a^2}+\sqrt{b^2}=|a|+|b|\)
\(\LARGE =-a+b\)
می‌توانیم بقیۀ حالات را نیز به همین ترتیب بررسی کنیم:
- اگر \(\Large a\) مثبت و \(\Large b\) منفی باشد، آنگاه \(\Large \sqrt{a^2}+\sqrt{b^2}=a-b\)
- اگر \(\Large a\) مثبت و \(\Large b\) مثبت باشد، آنگاه \(\Large \sqrt{a^2}+\sqrt{b^2}=a+b\)
- اگر \(\Large a\) منفی و \(\Large b\) منفی باشد، آنگاه \(\Large \sqrt{a^2}+\sqrt{b^2}=-a-b\)
به قسمت بعدی از درسنامۀ ریشه گیری ریاضی نهم توجه کنید.
ریشۀ سوم عدد
اگر ریشۀ دوم یک عدد را به توان دو برسانیم برابر با خود عدد خواهد شد. با توجه به این نکته می‌توانیم ریشۀ سوم یک عدد را نیز تعریف کنیم. ریشۀ سوم یک عدد برابر با عددی است که اگر به توان سه برسانیم برابر با خود عدد می‌شود. مثلاً ریشۀ سوم عدد \(\Large 8\) برابر با عدد \(\Large 2\) است زیرا \(\Large 2^3\) برابر با \(\Large 8\) است. در حالت کلی، ریشۀ سوم عدد حقیقی \(\Large a\) را با \(\Large \sqrt[3]{a}\) نمایش می‌دهیم. برای اینکه در ابتدای کار کمی بیشتر آشنا با ریشۀ سوم آشنا شوید، ریشۀ سومِ مکعبِ اعداد یک رقمی مثبت و منفی را در دو جدول زیر آورده‌ایم:
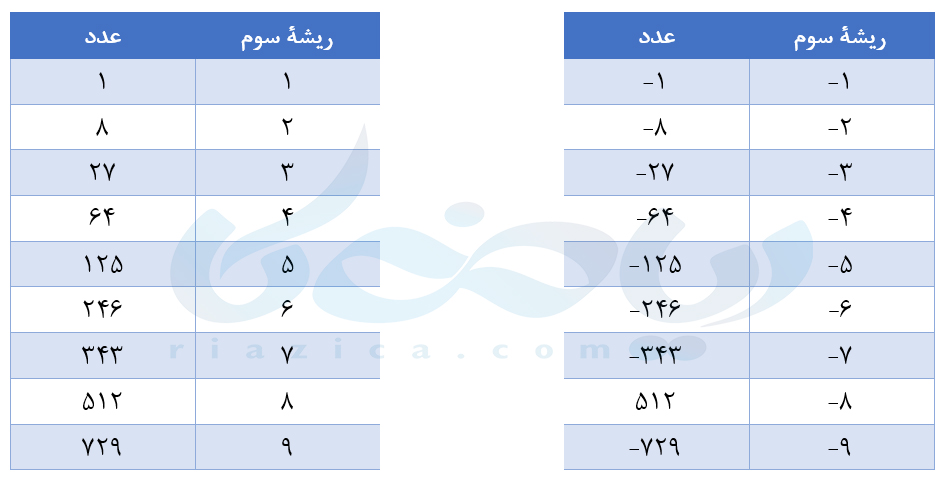
در مجموعۀ اعداد حقیقی هر عدد تنها یک ریشۀ سوم دارم. همچنین، برای اعداد منفی نیز ریشۀ سوم وجود دارد. ریشۀ سوم برخی از اعداد، برابر با یک عدد گویا نمی‌شود. روش به دست آوردن ریشۀ سوم تقریبی چنین اعدادی را در درسنامۀ آموزش ریشه گیری در ریاضی دهم خواهید آموخت. به مثال بعدی از درسنامۀ ریشه گیری ریاضی نهم توجه کنید.
مثال از ریشۀ سوم عدد
مثال 5: مقدار \(\Large \sqrt[3]{-125}\) را محاسبه کنید.
حل: باید به دنبال عددی باشیم که اگر آن را به توان سه برسانیم برابر با \(\Large -125\) شود. در صورتی که \(\Large -5\) را به توان سه برسانیم، برابر با \(\Large -125\) خواهد شد. بنابراین داریم:
\(\LARGE \sqrt[3]{-125}=-5\)
به قسمت بعدی از درسنامۀ ریشه گیری ریاضی نهم توجه کنید.
ضرب و تقسیم رادیکال ها
در پایۀ هشتم آموختید که برای اعداد مثبت \(\Large a\) و \(\Large b\)، دو رابطۀ زیر برقرار است:
\(\LARGE \sqrt{ab}=\sqrt{a}\times \sqrt{b}\)
\(\LARGE \sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)
رابطۀ اول بیان می‌کند که ریشۀ دوم حاصل ضرب دو عدد مثبت، برابر است با حاصل ضرب ریشۀ دوم هر یک از آن‌ها. رابطۀ دوم نیز می‌گوید، ریشۀ دوم تقسیم دو عدد مثبت، برابر است با تقسیم ریشۀ دوم آن‌ها. مشابه این روابط برای ریشۀ سوم نیز برقرار است. یعنی داریم:
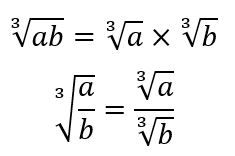
البته باید دقت کنید که رابطۀ آخر فقط به ازای \(\Large b \neq 0\) برقرار است. مطابق با دو رابطۀ آخر، ریشۀ سوم حاصل ضرب دو عدد، برابر است با حاصل ضرب ریشۀ سوم هر یک از آن‌ها. ریشۀ سوم تقسیم دو عدد (به شرط مخرج غیر صفر) نیز برابر است با تقسیم ریشۀ سوم آن‌ها. به مثال‌های بعدی از درسنامۀ ریشه گیری ریاضی نهم توجه کنید.
مثال از ضرب ریشه‌ها در ریشه گیری ریاضی نهم
مثال 6: حاصل عبارت \(\Large \sqrt[3]{9} \times \sqrt[3]{3}\) را به دست آورید.
حل: همان طور که گفتیم، حاصل ضرب ریشۀ سوم دو عدد برابر است با ریشۀ سوم حاصل ضرب آن‌ها. بنابراین داریم:
\(\LARGE \sqrt[3]{9} \times \sqrt[3]{3}=\sqrt[3]{9 \times 3}\)
\(\LARGE =\sqrt[3]{27}\)
\(\LARGE =3\)
به مثال بعدی از درسنامۀ ریشه گیری ریاضی نهم توجه کنید.
مثال 7: حاصل عبارت \(\Large \sqrt[3]{-216}\) را به دست آورید.
حل: همان طور که گفتیم، ریشۀ سوم حاصل ضرب دو عدد، برابر است با حاصل ضرب ریشۀ سوم هر یک از آن‌ها. بنابراین داریم:
\(\LARGE \sqrt[3]{-216}=\sqrt[3]{-27} \times \sqrt[3]{8}\)
\(\LARGE =(-3) \times 2\)
\(\LARGE =-6\)
مثال از تقسیم ریشه‌ها در ریشه گیری ریاضی نهم
مثال 8: حاصل عبارت \(\Large \frac{\sqrt[3]{16}}{\sqrt[3]{2}}\) را به دست آورید.
حل: همان طور که گفتیم، ریشۀ سوم تقسیم دو عدد (به شرط مخرج غیر صفر)، برابر است با تقسیم ریشۀ سوم آن‌ها. بنابراین داریم:
\(\LARGE \frac{\sqrt[3]{16}}{\sqrt[3]{2}}=\sqrt[3]{\frac{16}{2}}\)
\(\LARGE =\sqrt[3]{8}\)
\(\LARGE =2\)
به مثال بعدی از درسنامۀ ریشه گیری ریاضی نهم توجه کنید.
مثال 9: حاصل عبارت \(\Large \sqrt[3]{\frac{-8}{125}}\) را به دست آورید.
حل: همان طور که گفتیم، ریشۀ سوم تقسیم دو عدد (به شرط مخرج غیر صفر)، برابر است با تقسیم ریشۀ سوم آن‌ها. بنابراین داریم:
\(\LARGE \sqrt[3]{\frac{-8}{125}}=\frac{\sqrt[3]{-8}}{\sqrt[3]{125}}\)
\(\LARGE =\frac{-2}{5}\)
در ادامه حتما درسنامه جمع وتفریق رادیکالها را مطالعه کنید.
ویدیو از ریشه گیری ریاضی نهم
در این ویدیو چند نمونه سوال از ریشه گیری وساده کردن رادیکالهای ریاضی نهم آموزش شده است.
زنگ آخر کلاس ریشه گیری ریاضی نهم
در این درسنامه از ریاضی نهم مرور کوتاهی کردیم بر مطالبی که در مورد ریشۀ دوم در سال‌های گذشته خوانده بودید. همچنین، بر اساس مطالبی که در مورد ریشۀ دوم گفتیم، ریشۀ سوم اعداد حقیقی را معرفی کردیم. دیدیم مشابه روابطی که در مورد ضرب و تقسیم ریشه‌های دوم بر قرار بود، برای ریشۀ سوم نیز صدق می‌کرد.
ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث ریشه گیری ریاضی نهم دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.
عالللی
با سلام وعرض ادب
ممنون از توجه شما
سلام لطفا جواب این سوال روبگین:ریشه سوم عبارت۱۵رادیکال۳+۲۶
با سلام وعرض ادب
این چیزی که شما نوشتید ساده نمیشه
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام خیلی ممنون بابت توضیحاتتون
با سلام وعرض ادب
خدا رو شکر که برای شما مفید واقع شده.
وایییییی هرچقدر تشکررر منم بازممم کمه خیلیی عالی بودننن
من شنبه امتحان دارم امیدوارم نتیجه خوبی بگیرممم
با سلام وعرض احترام
واقعا از دیدن این چنین پیامهایی دلگرم وخریند میشویم ممنون از توجه شما
عالی بود مچکرم.
با سلام واحترام
ممنون دوست عزیز
واقعا ازتون متشکرم
مطالب عالی و مفید بودن
خدا قوت خسته نباشید..
با عرض سلام واحترام
ممنون وخدا روشکر که استفاده لازم رو بردید
صعلام مطالب عالی بود ممنون عزتون:) ♡
با سلام و عرض ادب
ممنون از دیدگاه پر انرژی شما
سلام خیلی خوب بوداطلاعات ساده ولی عالی گرفتم امیدوارم فرداتوامتحانم ازاین مطالبتون نتیجه خوبی بگیرم
با سلام واحترام
خدا رو شکر که مفید بوده انشالله که نتیجه عالیبگیرید
بد بود
با سلام وعرض ادب
دوست عزیز کاش مشخص کنید از چه نظر ؟
سلام، تو بخش ریشهٔ سوم، تو تصویری که اعدادی که ریشه‌های طبیعی ۱ تا ۹ دارن رو نوشتین، دو تا اشتباه هست.
۱ – ریشه سوع عدد ۲۱۶ میشه ۶ نه ۲۴۶ که شما نوشتید. خودتون پایینتر جواب درست رو نوشتید.
۲ – تو اعداد منفی، یکی از اعداد رو بدون منهی (-) نوشتید.
با سلام وعرض ادب
ممنون از شما ودقت نظرتون اصلاج میشه
ممنونم هیچ سایتی مثل سایت شما نگفته بود♡
با سلام وادب
درست میفرمایید هیچ سایتی به اندازه ما وقت وهزینه برای مطالب رایگان نمیکنه
سلام ریشه سوم 17چطوری بدست میاد
با سلام
این عدد بین دو عدد ۸ و۲۷ که هر دو مکعب کاملن پس ریشه سوم آن ۲ وخورده ای میشه که در پست پیدا کردهن اعشارش رو توضیح دادیم
سلام ببخشید ریشه سوم ۱۶ چی میشه ؟؟ و اینکه ریشه دوم ۱۶ عدد ۴ هست؟
با سلام
ریشه سوم ۱۶ میشخ ۲رادیکال دو یعنی ریشه کاملنداره وریشه دوم ۱۶ میشه چهار ومنفی چها هر عدد دوریشه زوج داره
واقعا ممنون من ازشون استفاده کردم وبرای خودم تمرینحل کردم خیلی خوب بود ❤❤❤❤❤❤❤
با سلام
خوشحالم مفید بوده
عالی بود ممنون از تلاشتون خیلی بدرد بخور وکارامد بود امروز هم امتحان دارم دعا کنید
مرسی
با یلام وروز به خیر
خدا یاور شما هست اگه تلاش کردید
عالی بود
عالی
با سلام
ممنون از نظر لطف شما
40500 چی میشه؟
هیچی?
سلام دوست عزیز
چی هیچی؟؟؟
واقعا عالی بود مطالب تون با یک بار خوندن کاملا متوجه شدم ممنونمممم💓
واقعا خیلی ممنون عالیی بودن
خیلی خوب جمع بندی شده بود
خیلی خوب متوجه شدم
ممنون