آموزش ریاضی پایه هفتم
عدد اول ریاضی هفتم 🧩📏 – فقط دو شمارنده!
در درسنامۀ عدد اول ریاضی هفتم ابتدا تعریف میکنیم شمارندههای یک عدد طبیعی، چه اعدادی هستند. سپس خواهیم گفت که اعدادی که تنها دو شمارنده دارند، اعداد اول نامیده میشوند. تمام بحث ما در این درسنامه در مورد اعداد طبیعی است. بنابراین، تعاریفی که ارائه میکنیم تنها در مورد اعداد طبیعی صادق است. سعی میکنیم با حل مثالهای مختلف از درسنامۀ عدد اول ریاضی هفتم، در درک بهتر مبحث به شما کمک کنیم.
شمارنده چیست؟
زمانی که باقیماندۀ تقسیم عددی مانند \(\Large a\) بر عدد \(\Large b\) صفر باشد، میگوییم \(\Large a\) بر \(\Large b\) بخش پذیر است. همچنین عدد \(\Large b\) را شمارندۀ عدد \(\Large a\) میگوییم. مثلاً، عدد \(\Large 2\) شمارندۀ عدد \(\Large 12\) است؛ زیرا داریم:
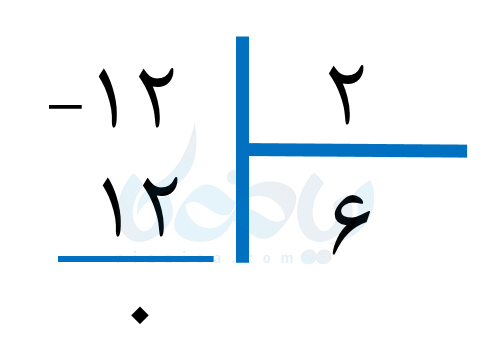
همانطور که میبینید، باقیماندۀ تقسیم \(\Large 12\) بر \(\Large 2\) برابر با صفر است. در نتیجه، \(\Large 2\) شمارندۀ \(\Large 12\) است.
نکته:به شمارنده های یک عدد مقسوم علیه های اون عدد هم گفته می شود.
به مثالهای بعدی از درسنامۀ عدد اول ریاضی هفتم توجه کنید.
مثال از شمارنده
مثال 1: شمارندههای عدد \(\Large 6\) را پیدا کنید.
حل: برای یافتن شمارندههای عدد \(\Large 6\) کافی است ببینیم این عدد بر چه اعدادی بخش پذیر است. یعنی باید ببینیم باقیماندۀ تقسیم \(\Large 6\) بر چه اعدادی برابر با صفر است. باقیماندۀ تقسیم \(\Large 6\) بر اعداد \(\Large 1\) و \(\Large 2\) و \(\Large 3\) و \(\Large 6\) برابر با صفر است. یعنی میتوانیم \(\Large 6\) را به صورت حاصل ضرب هر یک از این اعداد با عددی دیگر بنویسیم:
\(\LARGE 6= 1 \times 6\)
\(\LARGE 6= 2 \times 3\)
\(\LARGE 6= 3 \times 2\)
\(\LARGE 6= 6 \times 1\)
بنابراین اعداد \(\Large 1\) و \(\Large 2\) و \(\Large 3\) و \(\Large 6\) شمارندههای عدد \(\Large 6\) هستند. به مثال بعدی از درسنامۀ عدد اول ریاضی هفتم توجه کنید.
مثال 2: ثابت کنید عدد \(\Large 7\) شمارندۀ \(\Large 25\) نیست.
حل: کافی است نشان دهیم باقیماندۀ عدد \(\Large 25\) بر \(\Large 7\) مخالف صفر است:
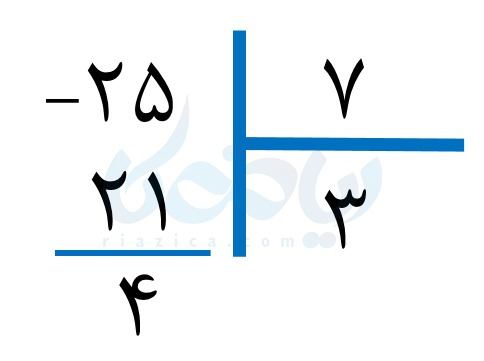
همان طور که میبینید، باقیماندۀ تقسیم \(\Large 25\) بر \(\Large 7\) برابر با \(\Large 4\) است؛ یعنی مخالف صفر است. بنابراین \(\Large 7\) شمارندۀ \(\Large 25\) نیست. به قسمت بعدی از درسنامۀ عدد اول ریاضی هفتم توجه کنید.
نکاتی در مورد شمارنده
در مورد شمارندهها، نکات زیر وجود دارد:
- عدد \(\Large 1\) شمارندۀ همۀ اعداد است. زیرا هر عددی بر \(\Large 1\) بخش پذیر است.
- عدد \(\Large 1\) کوچکترین شمارندۀ هر عددی است.
- بزرگترین شمارندۀ هر عدد، خودِ عدد است. زیرا هر عددی بر خودش بخش پذیر است. از طرفی هیچ عددی بر اعداد بزرگتر از خود بخش پذیر نیست.
- هر عدد بزرگتر از \(\Large 1\)، حداقل دو شمارنده دارد. یکی عدد \(\Large 1\) و دیگری خود عدد.
طبق نکتۀ آخر، در بین اعداد بزرگتر از \(\Large 1\)، هیچ عددی نیست که کمتر از دو شمارنده داشته باشد. اما اعدادی هستند که بیشتر از دو شمارنده دارند که به آنها عدد مرکب می گویند.. مثلاً عدد \(\Large 6\) که در مثال یک دیدیم چهار شمارنده دارد یک عدد مرکب است. به قسمت بعدی از درسنامۀ عدد اول ریاضی هفتم توجه کنید.
تعریف عدد اول
به اعدادی طبیعی بزرگتر از یک که فقط دو شمارنده دارند، اعداد اول میگوییم. همان طور که در قسمت قبل گفتیم، این دو شمارنده، خودِ عدد و عددِ \(\Large 1\) هستند. عدد \(\Large 1\) اول نیست چون فقط یک شمارنده دارد. عدد \(\Large 2\) اول است، چون دو شمارنده دارد. \(\Large 1\) و \(\Large 2\) شمارندههای عدد \(\Large 2\) هستند. اعداد \(\Large 3\) و \(\Large 5\) و \(\Large 7\) نیز، اعداد اول هستند. در سالهای آینده اثبات خواهیم کرد که اعداد اول نامتناهی هستند. به مثالهای بعدی از درسنامۀ عدد اول ریاضی هفتم توجه کنید.
مثال از عدد اول
مثال 3: آیا امکان دارد یک عدد زوج، عدد اول باشد؟
حل: تنها عدد زوجی که اول است، عدد \(\Large 2\) است. عدد \(\Large 2\) تنها بر خودش و یک بخش پذیر است. اما بقیۀ اعداد زوج، هم بر \(\Large 1\)، هم بر \(\Large 2\) و هم بر خودشان بخش پذیر هستند. یعنی اعداد زوج بزرگتر از \(\Large 2\) حداقل سه شمارنده دارند. در نتیجه، تنها عدد زوجِ اول، عدد \(\Large 2\) استو بقیه اعداد اول فرد هستند. به مثال بعدی از درسنامۀ عدد اول ریاضی هفتم توجه کنید.
حاصل ضرب دو عدد اول ریاضی هفتم
مثال 4: آیا حاصل ضرب دو عدد اول، اول است؟
حل: حاصل ضرب دو عدد اول، هیچگاه اول نیست. تفاوتی نمیکند که آن دو عدد اول یکسان باشند یا متفاوت. زیرا در هر صورت، حاصل ضرب آنها بر \(\Large 1\)، یکی از اعداد اول که در هم ضرب شده و خود عدد بخش پذیر است. در نتیجه، حاصل ضرب دو عدد اول حداقل سه شمارنده دارد. مثلاً حاصل ضرب عدد \(\Large 2\) در خودش، دارای شمارندههای \(\Large 1\) و \(\Large 2\) و \(\Large 4\) است. یا به طور مثال، حاصل ضرب \(\Large 2\) در \(\Large 3\)، دارای شمارندههای \(\Large 1\) و \(\Large 2\) و \(\Large 3\) و \(\Large 6\) است. بنابراین حاصل ضرب دو عدد اول هیچ گاه اول نمیشود. به مثال بعدی از درسنامۀ عدد اول ریاضی هفتم توجه کنید.
حاصل جمع دو عدد اول ریاضی هفتم
مثال 5: آیا حاصل جمع دو عدد اول، اول است؟
حل: اگر هر دو عدد اول فرد باشند (مخالف \(\Large 2\) باشند)، حاصل جمع آنها عدد زوجی بزگتر از \(\Large 2\) خواهد شد. در نتیجه اول نخواهد بود. اما اگر یکی از آنها زوج باشد (عدد \(\Large 2\) باشد)، حاصل جمعشان هم میتواند اول باشد و هم غیر اول. مثلاً حاصل جمع \(\Large 2\) و \(\Large 3\) برابر با \(\Large 5\) است که عددی اول است. اما حاصل جمع \(\Large 2\) و \(\Large 7\) برابر با \(\Large 9\) است که اول نیست. زیرا شمارندههای آن، اعداد \(\Large 1\) و \(\Large 3\) و \(\Large 9\) هستند.
برای خوندن ادامه مطلب پست شمارنده اول ریاضی هفتم وبرای یادگیری مطالب بیشتر در مورد اعداد اول پست اعداد اول ریاضی هشتم رو مطالعه کنید
زنگ آخر کلاس عدد اول ریاضی هفتم
در این درسنامه با مفهوم شمارنده آشنا شدیم. دیدیم که هر عدد بزرگتر از \(\Large 1\)، حداقل دو شمارنده دارد. به اعدادی که تنها دو شمارنده داشتند، اعداد اول گفتیم. همچنین، در مثالهای انتهایی درسنامه، حاصل ضرب و حاصل جمع اعداد اول را بررسی کردیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با این مبحث دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





عالییییییییییییی
سلام دوست عزیز
ممنون که براتون مفید بوده
عالللللللیییییی
ممنون از شماااااا
ممنون از شماااااا دوست عزیز
ممنون
با سلام وعرض ادب واحترام
خواهش میکنیم خدا رو شکر که مفید واقع شده
سلام خیلی متشکرم بابت توضیحاتتون
خیلی مفید و آموزنده بود
با سلام و عرض ادب
ممنون از نظر شما وخوشحالیم مفید بوده برای شما
خیلی ممنون عالی بود
خدا رو شکر که این پست اینهمه مورد توجه دوستان قرار گرفته
عالی بود
با سلام وعرض احترام
ممنون از نگاه پر مهر شما
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام
لطفا بهم میگین که عدد ۵۰۴ چند شمارنده داره
ممنون
با سلام وعرض ادب
۲۴ تا ۱و۲و۳و۴و۶و۷و۸و۹و۱۲و۱۴و۱۸و۲۴و۲۸و۳۶و۲۱و۴۲و۵۶و۶۳و۷۲و۸۴و۱۲۶و۱۶۸و۲۵۲و۵۰۴
سلام و عرض ادب ?
ممنون عالی بود?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
سلام وعرض ادب
ممنون از توجه شما
سلام
بسیار عالی،عالییی
با سلام وعرض ادب
ممنون از توجه شما
عدد اول را تعریف کنید
با سلام وادب
هر عدد طبیعی بزرگتراز یک که به جز خودش ویک بر عدد دیگری بخش پذیر نباشد را عدد اول میگویند
واقعا عالی بود
واقعا عالی بود دستتون درد نکنە
با سلام واحترام خوشحالیم که مفید بوده
مرسی واقعا عالی بود ❤️
سلام
عالی بسیار عالی?
با سلام واحترام
ممنون از شما دوست عزیز
خیلی ممنون عالی بود ❤❤❤
با سلام عرض ادب
خدا رو شکر مفید واقع شده
ممنون واقعا
با سلام عرض ادب
ممنون از نظر لطف شما
سلام آیا تمام عددهای اول فرد هستند
با سلام وعرض ادب
به غیر از دو که زوج هست بقیه فرد هستن
عالی بود ممنون خیلی خیلی کمکم کرد
با سلام و احترام
خدا رو شکر که مفید واقع شده
??????میسیو
ممنون خوب بود ????
با سلام واحترام
خواهش میکنم
ببخشید میشه بگید چطوری با سرعت بالا میتونیم تعداد شمارنده های یک عدد بزرگ رو پیدا کنیم ممنون…. متنتون هم خیلی مفید بود. باتشکر
با سلام وعرض ادب
کافیه اول ببینید به چه عددهای اولی بخش پذیره بعد سروع کنید به شمارندهای اولش تقسیم کنید قبلا در کتاب با استفاده از شمارنده های اول عدد ورسم نمودار سریع بچه ها به تمام شمارنده ها دست پیدا میکردن که الان از کتاب برداشته شده
خوب بود ولی تشخیص اعداد اول را نگفتید .
با سلام وعرض ادب
در پستهای دیگه گفتیم حتما ببینید
سلام دوست عزیز
به این پست مراجعه کنیدhttps://riazica.com/prime-number/#comment-10911
عالی
خیلی خوب بود
با سلام وعرض وادب
ممنون از شما
سلام
عالی بود ممنون
یک سوال داشتم
ایا هیچ دوعدد اولی بر هم بخش پذیر نیستن؟ یا هستن؟
با سلام وعرض ادب
خیر اگر بخش پذیر باشند که دیگه اول نیستند
عالییییییی واقعا نکات خوبی بود ممنونم
با سلام وعرض احترام
ممنون از نظر لطف شما
خوب بود تشکر
ممنون میشم بهم بگید حاصل تقسیم دو عدد اول چی میشه
با سلام
یک عدد گویا میشه
سلام واقعا عالیه من کاملا عدد اول و شمارنده رو یاد گرفتم خیلی ممنون
با سلام و وقت به خیر
خوشحالیم که به هدفمون رسیدیم
عالییییی ممنووون از شما
با سلام
ممنون از توجه شما
خیلی عالیه واقعا من هیچی بلد نبودم ولی الان کامل یاد گرفتم.سایت رو هم به دوستام معرفی خواهم کرد
با سلام وادب
خیلی خرسندیم که مطالب ما برای شما مفید بوده
ببخشید عدد اول ۲۹ است
با سلام
۲۹ عدد اول هست
خیلی خوب بود واقعا ممنونم
با سلام وقت به خیر
سپاس خدا رو که تونستیم مفید واقع بشیم
بسیار آموزنده بود باتشکر از مدیریت سایت
با سلام وادب
ممنون از نظر شما
سلام میشه برای من اعداد اول را تا هر چی ادامه داره به من بگید
سلام دوست عزیز خودتون با روشی که در پست زیر گفته شده پیدا کنیدhttps://riazica.com/prime-number/#comment-10911
دراین وبلاگ جوابتون رو بگیریدhttp://www.997.blogfa.com/post/20
چگونه میتونم بفهمم که یک عدد اول هست یا نه
سلام ب روشی که در این پست گفته شدهhttps://riazica.com/prime-number/#comment-10911
عالی ممنون که مطالب مفید بهتری رو گذاشتین
با سلام واحترام
ممنون از نظر شما دوست عزیز
عاااااااااااااااااااااااالی
با عرض سلام وادب
ممنون از نگاه شما
تمام اعداد اول فرد هستند
سلام دوست عزیز به غیر عدد دو بقیه فرد هستند
افتضاح این چه توضیحی بود ؟
سلام عزیزم
کجاش مشکل داشت؟
اقا دمتون گرم توضیحات عالی از خود کتابم بهتر بود
با سلام
ممنون از انرژی که به ما برای ادامه راه میدهید
عالی بود فقط میشه بگید شمارنده های یک عدد چگونه پیدا میکنیم ؟
با سلام
دوست عزیز پست مربوط به اون رو گذاشتیم برید بخونید
عالیی ممنون از شما
سلام دوست عزیز
ممنون از محبت شما
عالی بود
با سلام
ممنون از نظر شما
واقعاً دستتون درد نکنه سایتتون محشر من ترکم تبریزی اما تو چابهار درس میخونم معلم مون قرار امتحان بگیره واسه همین دارم هفتم و مرور میکنم امسال هشتمم بازم تشکر میکنم دستتون درد نکنه
سلام دوست عزیز
انشاالله سال تحصیلی خوبی پیش رو داشته باشی
سلام واقعا جزوه ی ریاضیتون عالی بود خیلی سپاس گزارم (◠‿◕) (◍•ᴗ•◍) ❤
مفید بود
فقط ……….. عدد اول داریم که رقم هایش تکراری است ( یک یا دو )
میشه جای خالی رو بگین
سلام دوست عزیز
۱۱هر دو عددش تکراری هست واول پس فقط یک عدد اول داریم که ارقامش تکراری است
عالی بود
سلام ببخشید!
تعریف غیر اول روهم بگید بیزحمت♡
با سلام هر عدد که اول نباشد غیر اول است
اصلا از این ها توی امتحان نیومد و خیلی فرق می کرد با معلم های دیگه و باید بیشتر توضیح دهید ممنون
ما در اینجا مفاهیم رو تدریس می کنیم اگر اصل مطلب رو درک کنی میتونی به همه سوالات امتحان جواب بدی
واقعا بهترین و کاملترین جزوه بود ممنون خیلی بهم کمک کرد ❤️
ممنون از نگاه شما