آموزش ریاضی پایه نهم
اعداد حقیقی ریاضی نهم 🌐✅ – همه عددهای که میشناسید!
در مبحث اعداد حقیقی ریاضی نهم با یکی دیگر از مجموعههای اعداد آشنا میشویم؛ مجموعۀ اعداد حقیقی. قبل از آشنایی با این مجموعۀ ویژه، لازم است اعداد گنگ را بشناسیم. بنابراین بعد از مروری کوتاه بر اعداد گویا، اعداد گنگ را معرفی کرده و سپس سراغ اعداد حقیقی خواهیم رفت. درسنامه را طوری تنظیم کردیم که پس از مطالعۀ آن هیچ مشکلی در درک درس نداشته باشید. با ما تا انتها همراه باشید!
یادآوری اعداد گویا
همانطور که در پایۀ هشتم خواندید، از تقسیم یک عدد صحیح بر یک عدد صحیح غیر صفر، عدد گویا به وجود میآید (در صورتی که نیاز به مرور مبحث اعداد گویا دارید، درسنامۀ تعریف اعداد گویا را مطالعه کنید). اعداد گویا را میتوانستیم به صورت اعشاری نیز نمایش دهیم. در این صورت دو حالت داشتیم:
- اعداد گویا با تعداد ارقام اعشاری متناهی. مثلاً عدد گویای \(\Large \frac{2}{5} \) که همان \(\Large 0.4 \) است و تنها یک رقم اعشار دارد.
- اعداد گویا با تعداد ارقام اعشاری نامتناهی ولی متناوب. متناوب به این معنی که یک یا چند رقم اعشار در این اعداد تکرار میشوند. مثلاً عدد گویای \(\Large \frac{1}{3} \) که همان \(\Large 0.333\dots \) است و در آن رقم اعشار 3 متناوباً تکرار میشود.
اعداد گنگ چیستند؟
برخی از اعداد اعشاری در هیچ یک از دو دستۀ بالا قرار نمیگیرند. مثلاً در زیر، عدد \(\Large \pi \) را تا چند رقم اعشار نوشتهایم:
\(\Large \pi=3.14159265 \)
تعداد ارقام اعشاری عدد \(\Large \pi \) نامتناهی و غیر متناوب است. یعنی اگر ارقام اعشاری عدد \(\Large \pi \) که از تقسیم محیط بر قطر دایره به دست میآید را بنویسیم، نه اعشار صفر میشود و نه هیچ تعدادی از اعشاری به صورت پشت سر هم تکرار میشوند. به این اعداد که دارای تعداد ارقام اعشاری نامتناهی و نامتناوب هستند، اعداد گنگ (اصم) میگوییم. مجموعۀ اعداد گنگ را با \(\Large Q’ \) یا \(\Large Q^c \) نمایش میدهیم. \(\Large \sqrt{2} \) و \(\Large \sqrt{5} \) نیز نمونههای دیگری از اعداد گنگ هستند. به طور کلی ریشۀ دوم هر عددی که مربع کامل نباشد، گنگ است (در سالهای آینده اثبات این قضیه را خواهید دید). مثال بعد، یک مثال مهم از مبحث اعداد حقیقی ریاضی نهم است که غالباً دانشآموزان در حل آن دچار مشکل میشوند.
مثال از اعداد گنگ
مثال 1: عدد \(\Large 0.020020002\dots \) عددی گویا است؟
حل: ممکن است به اشتباه بگویید بله! اما این عدد گویا نیست. دلیل این اشتباه این است که فکر میکنیم هر نظمی که در ارقام اعشاری وجود داشته باشد، به معنای وجود تناوب در آن است؛ اما وجود نظم در قسمت اعشاری به معنی وجود تناوب یا همان تکرار در آن نیست. زمانی در ارقام اعشاری تناوب وجود دارد که تعدادی از آنها از جایی به بعد بدون فاصله تکرار شوند. در ارقام اعشاری عدد بالا نظم وجود دارد اما تناوبی وجود ندارد. بنابراین این عدد، گنگ است.
نمودار ون مجموعۀ اعداد گنگ
با مجموعۀ اعداد طبیعی، صحیح و گویا قبلاً آشنا شدهاید. اگر بخواهیم مجموعۀ اعداد گنگ را نیز در کنار آنها در یک نمودار ون نمایش دهیم، نمودار زیر حاصل خواهد شد:
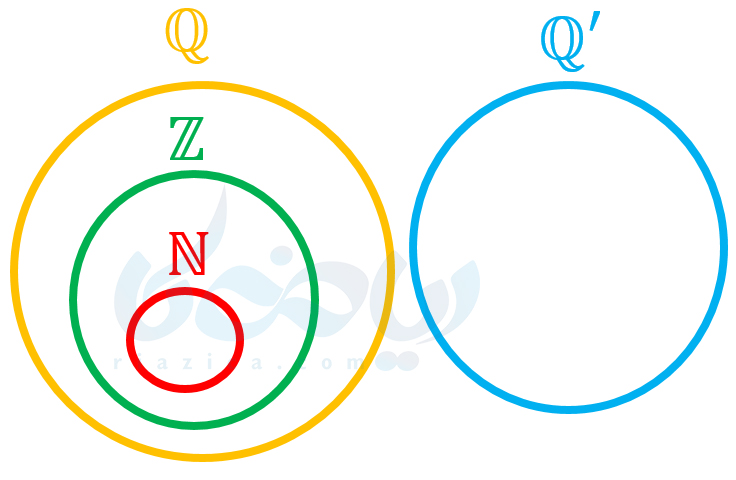
همانطور که میبینید، مجموعۀ اعداد طبیعی، زیرمجموعۀ اعداد صحیح و مجموعۀ اعداد صحیح، زیرمجموعۀ اعداد گویا هستند. در ضمن، هیچ یک از این سه مجموعه، اشتراکی با مجموعۀ اعداد گنگ ندارد.
نمایش برخی از اعداد گنگ روی محور
ما در درسنامه نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم به طور مفصل در مورد رسم اعداد گنگ روی محور صحبت کردیم حال میخواهیم عدد \(\Large \sqrt{2} \) که یک عدد گنگ است را روی محور نمایش دهیم (نمایش اعداد رادیکالی روی محور به صورت مفصل در درسنامۀ نمایش اعداد رادیکالی بررسی شده است. البته در اینجا نیز به صورت مختصر آن را مرور میکنیم). به نظر غیر ممکن میآید. زیرا \(\Large \sqrt{2} \) یک عدد اعشاری با تعداد نامتناهی رقم اعشار است و از تقسیم هیچ دو عدد صحیحی به دست نمیآید؛ اما با جود آنچه گفته شد، میتوانیم \(\Large \sqrt{2} \) را روی محور نمایش دهیم. یک مثلث قائمالزاویه در نظر بگیرید. اگر طول هر کدام از اضلاع عمود بر هم یک باشد، طبق قضیۀ فیثاغورس، وتر آن برابر با \(\Large \sqrt{2} \) خواهد بود. از این موضوع استفاده میکنیم و روی محور، مانند شکل زیر، یک مثلث قائمالزاویه رسم میکنیم:
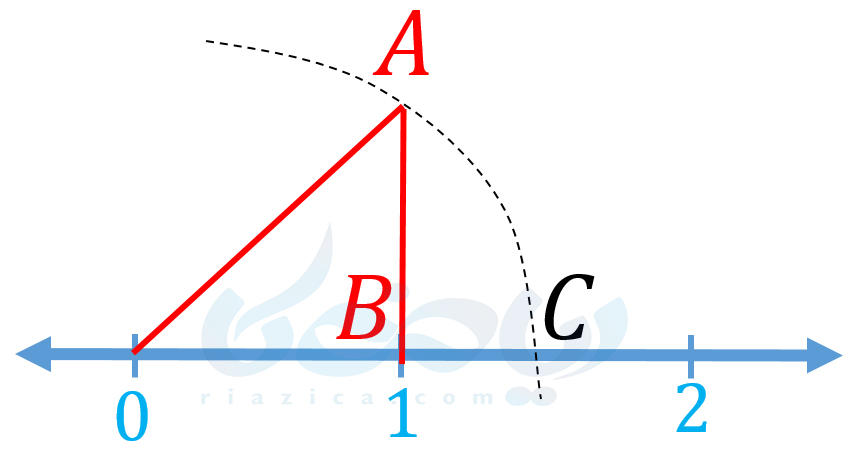
وتر مثلث ABO برابر با \(\Large \sqrt{2} \) است. بنابراین اگر دهانۀ پرگار را به اندازۀ پاره خط OA باز کرده و کمانی رسم کنیم، محل تقاطع این کمان با محور، که همان نقطۀ C میباشد، عدد \(\Large \sqrt{2} \) را روی محور اعداد نشان میدهد. به مثال بعدی از مبحث اعداد حقیقی ریاضی نهم دقت کنید.
مثال از نمایش عدد گنگ روی محور
مثال 2: عدد \(\Large \sqrt{5} \) را روی محور نشان دهید.
حل: \(\Large \sqrt{5} \) را میتوانیم به صورت \(\Large \sqrt{4+۱} \) بنویسیم. بنابراین اگر مثلث قائمالزاویهای داشته باشیم که اضلاع عمود بر هم آن دارای اندازۀ 1 و 2 باشند، اندازۀ وتر مثلث، \(\Large \sqrt{5} \) خواهد بود. به شکل زیر دقت کنید:
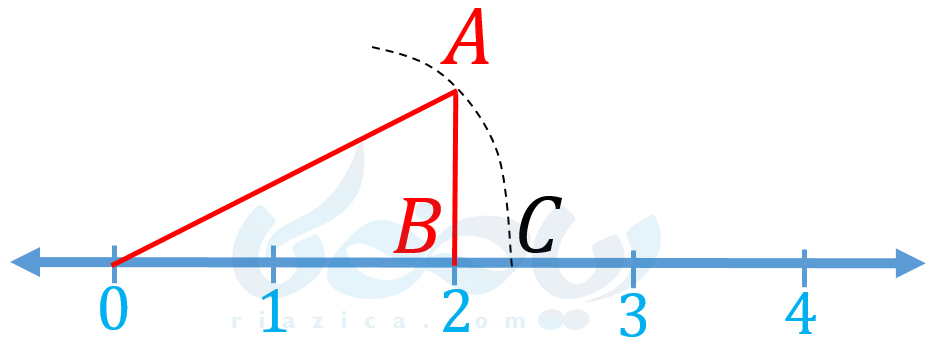
در شکل بالا اندازۀ AB را برابر با 1 گرفتیم. بنابراین، اندازۀ OA برابر با \(\Large \sqrt{5} \) بوده و نقطۀ C عدد \(\Large \sqrt{5} \) را روی محور اعداد نشان میدهد.
عدد گنگ بین دو عدد دلخواه
در درسنامۀ اعداد گویا دیدیم که بین هر دو عدد گویا میتوان به تعداد دلخواه عدد گویای دیگر پیدا کرد. در مورد اعداد گنگ نیز میتوانیم همین کار را انجام دهیم. به مثال بعدی از مبحث اعداد حقیقی ریاضی نهم دقت کنید.
مثال 3: یک عدد گنگ بین 2 و 3 بیابید.
حل: 2 همان \(\Large \sqrt{4} \) و 3 همان \(\Large \sqrt{9} \) است. \(\Large \sqrt{5} \) بین \(\Large \sqrt{4} \) و \(\Large \sqrt{9} \) است. از طرفی همان طور که گفتیم، ریشۀ دوم عددی که مربع کامل نیست، عدد گنگ است. بنابراین \(\Large \sqrt{5} \) هم گنگ است و هم بین \(\Large \sqrt{4} \) و \(\Large \sqrt{9} \) قرار دارد. به مثال بعدی از مبحث اعداد حقیقی ریاضی نهم دقت کنید.
مثال 4: سه عدد گنگ بین \(\Large \sqrt{6} \) و \(\Large \sqrt{7} \) پیدا کنید.
حل: کافی است مطابق با آنچه در درسنامۀ اعداد گویا گفتیم، سه عدد گویا بین 6 و 7 پیدا کنیم (البته باید دقت کرد که صورت و مخرج آن عدد گویا پس از ساده سازی، هر دو مربع کامل نباشند). میتوانیم 6 و 7 را در \(\Large \frac{5}{5} \) ضرب کنیم. در این صورت، اعداد \(\Large \frac{30}{5} \) و \(\Large \frac{35}{5} \) به دست میآیند. در نتیجه بین 6 و 7، سه عدد گویای زیر را داریم:
\( 6=\frac{30}{5}<\frac{31}{5}<\frac{32}{5}<\frac{33}{5}<\frac{35}{5} =7\)
ریشۀ دوم این سه عدد، بین ریشۀ دوم 6 و 7 قرار خواهد گرفت. یعنی داریم:
\( \sqrt{6}<\sqrt{\frac{31}{5}}<\sqrt{\frac{32}{5}}<\sqrt{\frac{33}{5}}<\sqrt{7} \)
از طرفی صورت و مخرج اعداد زیر رادیکال، مربع کامل نیستند. بنابراین سه عدد گنگ \(\Large \sqrt{\frac{31}{5}} \) و \(\Large \sqrt{\frac{32}{5}} \) و \(\Large \sqrt{\frac{33}{5}} \) بین \(\Large \sqrt{6} \) و \(\Large \sqrt{7} \) قرار دارند.
اعداد حقیقی ریاضی نهم
محور اعداد که در شکل زیر رسم شده است را در نظر بگیرید. اعداد بین 1 و 2 را با رنگ آبی نشان دادهایم.

همانطور که گفتیم، بین هر دو عدد گویا میتوان به تعدا دلخواه عدد گویا و عدد گنگ پیدا کرد. بنابراین در نقاط آبی رنگ بالا، هم عدد گویا و هم عدد گنگ وجود دارد. بنابراین نمیتوانیم بگوییم همۀ نقاط آبی رنگ در شکل بالا متعلق به \(\Large Q \) یا \(\Large Q^c \) هستند. اگر مجموعهای تشکیل دهیم که تمام اعداد گویا و گنگِ روی محور را شامل شود، به آن مجموعه، مجموعۀ اعداد حقیقی میگوییم و آن را با \(\Large \mathbb{R} \) نشان میدهیم. به عبارت دیگر، مجموعۀ اعداد حقیقی برابر است با اجتماع مجموعۀ اعداد گویا و مجموعۀ اعداد گنگ. یعنی داریم:
\(\LARGE \mathbb{R}=Q\cup Q’ \)
برای علاقهمندان (خارج از کتاب): ساخت اعداد حقیقی از اعداد گویا به شکل دقیق تری صورت میگیرد که در دبیرستان به آن نمیپردازیم. در صورتی که علاقهمندید میتوانید در مورد برش ددکیند تحقیق کنید.
نمودار ون مجموعۀ اعداد حقیقی ریاضی نهم
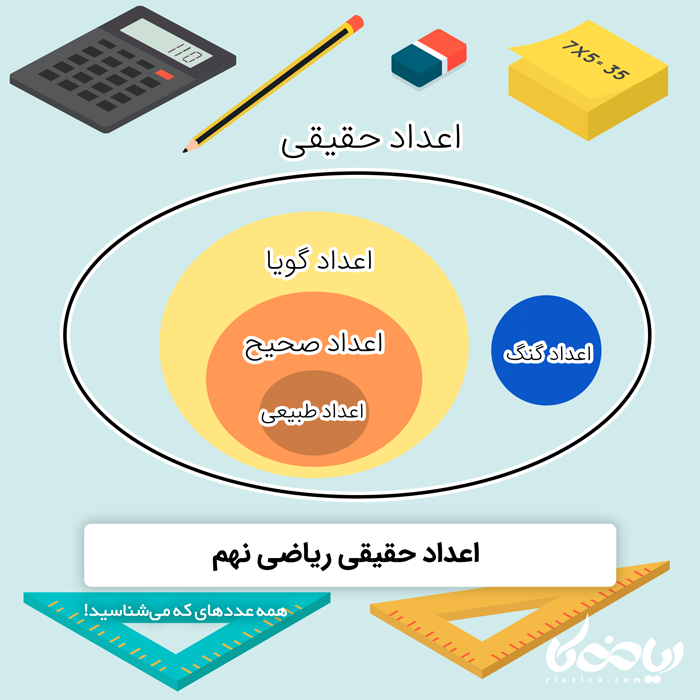
در حال حاضر با مجموعۀ اعداد طبیعی، صحیح، گویا، گنگ و حقیقی آشنا شدهایم. میتوانیم تمامی این مجموعهها را به صورت زیر در یک نمودار ون نمایش دهیم:
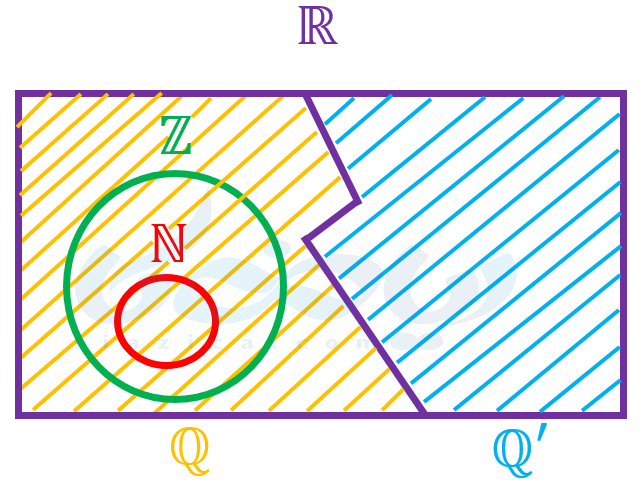
برای علاقهمندان (خارج از کتاب): توسعۀ اعداد به ساخت اعداد حقیقی ختم نمیشود. از اعداد حقیقی نیز، اعداد دیگری ساخته میشوند که به آنها اعداد مختلط میگویند. در صورتی که علاقهمندید میتوانید برای آشنایی، در مورد آنها تحقیق کنید.
مثال از اعداد حقیقی ریاضی نهم
مثال 5: اگر \(\Large A=\{x\in \mathbb{R}|-1<x<1\} \) و \(\Large B=\{x\in \mathbb{R}|2\leq x\leq 3\} \) باشد، \(\Large A\cup B \) را روی محور اعداد نمایش دهید.
حل: مجموعۀ A تمام اعداد بین \(\Large -1 \) و \(\Large 1 \) را روی محور اعداد شامل میشود. مجموعۀ B، تمام اعداد بین \(\Large 2 \) و \(\Large 3 \) و خود این دو عدد را روی محور اعداد شامل میشود. بنابراین اجتماع این دو مجموعه روی محور اعداد به شکل زیر نمایش داده میشود:

به مثال بعدی از مبحث اعداد حقیقی ریاضی نهم دقت کنید.
مثال 6: حاصل \(\Large (\mathbb{Z}\cup Q)\cup (\mathbb{R}-Q) \) را به دست آورید.
حل: حاصل هر پرانتز را جدا حساب کرده و در نهایت اجتماع دو پرانتز را به دست میآوریم. اعداد صحیح، زیر مجموعۀ اعداد گویا هستند. بنابراین داریم:
\(\LARGE \mathbb{Z}\cup Q=Q \)
اگر اعداد گویا را از اعداد حقیقی کنار بگذاریم، اعداد گنگ باقی میمانند. در نتیجه داریم:
\(\LARGE \mathbb{R}-Q=Q’ \)
از طرفی، اجتماع اعداد گویا و گنگ، مجموعۀ اعداد حقیقی را تشکیل میدهند. بنابراین با توجه به دو عبارت قبل داریم:
\(\LARGE (\mathbb{Z}\cup Q)\cup (\mathbb{R}-Q)=\mathbb{R} \)
زنگ آخر کلاس اعداد حقیقی ریاضی نهم
اعداد گنگ را شناختیم. دیدیدم که اعداد گنگ دستهای از اعداد اعشاری هستند که تعداد ارقام اعشاری آنها نامتناهی بوده و نامتناوب است. بعد از این، از اجتماع اعداد گویا و گنگ، اعداد حقیقی را ساختیم. در انتهای درسنامه نیز دو مثال مهم از مبحث اعداد حقیقی ریاضی نهم حل کردیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث اعداد حقیقی ریاضی نهم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.




عالی بود خیلی ممنون??
سلام دوست عزیز
ممنون از انرژی که دادید.
موفق باشید.
عالی بود خیلی ممنون??
سلام دوست عزیز
ممنون از حمایتی که می کنید.
موفق باشید.
واقا من فردا امتحان داشتم و نمیدونستم الان کامل فهمیدم ممنون❤️
با سلام
خدا رو شکر
ممنون عالی بود??
سلام و عرض ادب
ممنون از انرژی و پیام پرمهرتون.
موفق باشید
خیلی خوب بود ?
با سلام وعرض ادب
ممنون از توجه شما
سلام ممنونم از شما خیلی عالی و قابل فهم بود ?
با سلام وعرض ادب
خوشحالیم که مفید بوده
عالی بود ””’
ممنون از نگاه شما
سلام
پنج منهای رادیکال ۱۹بین کدام دو عدد صحیح متوالی قرار دارد؟ایا این عدد ب مجموعه xعضو اعداد حقیقی ب طوری ک xاز ۱-بزرگتر یا مساوی وxاز ۱کوچکترتعلق دارد؟
با سلام وعرض ادب
این عددی بین صفر ویک میباشد پس به مجموعه ای که میگویید تعلق دارد
عالی بود خیلی ممنون از آموزش شما
تا سلام وعرض ادب ممنون از شما
ممنون از شما
کدام نوع عدد هارا باA نشان میدهند؟
مثلا عدد های طبیعی را با Nنشون میدن
با سلام وعرض ادب
مجموعه خاصی زرو با A نمایش نمیدن
عالی
با سلام واحترام
خدا رو شکر
بسیار عالی توضیح دادید❤?
کیف کردم???
با سلام وعرض ادب
ممنون از نظر لطف شما
سلام وقت بخیر
مجموعه اعداد صحیح با نماد ریاضی چگونه نوشته می شود .
با سلام
با نماد z نشان میدهند
عالی
با سلام وادب
ممنون از شما
عالی حرف نداره
با سلام وادب
ممنون از دلگرمی شما
عالی و کامل
با سلام وادب
ممنون از نظر لطف شما
اعضای مجموعه R چیع؟؟
با سلام وادب
همان اعداد حقیقی هستن که شامل همه اعدادی هستن که میشناسید یعنی اعداد طبیعی و گویا وگنگ
فوق العاده بود
با سلام وادب
خرسندیم که این پست مورد پسند شما قرار گرفته
عالی بودید ??
با سلام وادب
ممنون از شما دوست عزیز
ممنون
با سلام وادب
خواهش میکنم
واقعا خدا خیرتون بده، تشکر
با سلام وادب
خواهش میکنم دوست عزیز
خوب بود اما کامل نبود مثلا تبدیل کسر به اعشار یا بر عکسش نبود
با سلام
ممنون از نظر شما
اعداد حقیقی چه اعدادی هستن شامل چیا میشن؟
مثلا اعداد طبیعی از یک تا ۹
پس اعداد حقیقی چطور؟
با سلام وادب
دوست عزیز همونطور که در این پست گفتیم هر عددی که تا الان شناختی از اعدادطبیعی مثل ۱و۲و۳و…. تااعداد گویا یا همون کسری واعداد گنگ همه رو بریزیم تو یه کیسه به همه اونها میگن اعداد حقیقی
اعداد حقیقی چه اعدادی هستن
با سلام وادب
اجتماع اعدادگویا وگنگ می شود اعداد حقیقی
اعداد حقیقی از چه عدد هایی شروع میشن مثلا حسابی از 0شروع میشه
با سلام وادب
اعداد حقیقی نه ابتدا دارن نه انتها واصلا قابل شمردن نیستن واصلا اعضای این مجموعه رو نمیشه با عضوهاش نوشت وبین هر دوعدد حقیقی بینهایت عدد حقیقی وجود داره
مختصر مفید و گویا . ممنون از مطالب اموزندتون
با سلام و ادب
خوشحالیم که به هدفمون رسیدیم
سلام و وقت بخیر بسیار عالی خسته نباشین
سلام وادب
ممنون از نظر لطف شما
عالی
با سلام
ممنون از نظر شما
استاد سلام و خداقوت 🙏🏻🙏🏻