تابع یک به یک 🌿☀️ – نظیر به نظیر!

در تعریف تابع در پست آموزشی گفتیم که تابع رابطه‌ای بین \( \Large x \) و \( \Large y \) است که به ازای هر \( \Large x \) فقط یک \( \Large y \) داشته باشیم به اصطلاح \( \Large x \)ها یا همان مولفه‌های اول در زوج مرتب تکراری نباشد.

تعریف تابع یک به یک

حال اگر در یک تابع به ازای هر \( \Large y \) نیز یک \( \Large x \) داشته باشیم یعنی \( \Large y \) تکراری نیز نداشته باشیم به این تابع، تابع یک به یک گفته می‌شود. یعنی بین \( \Large x \)ها و \( \Large y \)ها تناظر یک به یک وجود داشته باشد.

مثال ۱: آیا تابع زیر یک به یک است؟

\( \LARGE \{(2,1),(3,5),(-1,7),(4,2)\} \)

جواب ۱:

بله.

چون مولفه دوم تکراری نداریم. به ازای هر \( \Large y \) یک \( \Large x \) داریم.

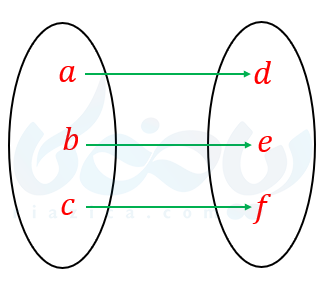
مثال ۲: کدام یک از توابع زیر یک به یک است؟

الف)

ب)

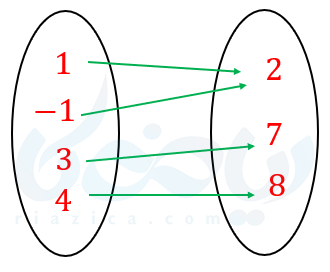
جواب ۲:

تابع  یک به یک نیست.

چون به ازای هر \( \Large x \) یک \( \Large y \) داریم.

\( \LARGE (1,2),(-1,2) \)

پس در نمودار ون این تابع باید از هر کدام از مولفه‌ها اول یک پیکان خارج و به هر یک از مولفه‌های دوم نیز یک پیکان وارد شود.

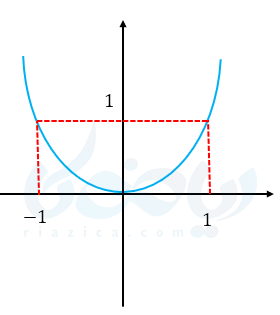
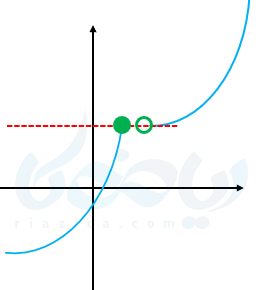
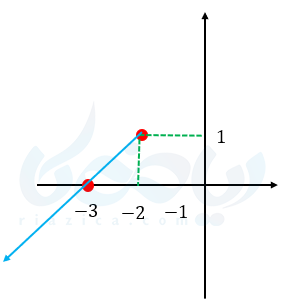
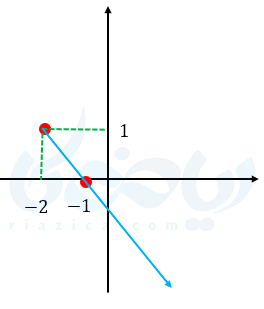
مثال ۳: آیا نمودارهای زیر یک توابع یک به یک را نشان می‌دهند؟

الف)

ب)

جواب ۳:

نمودار الف یک تابع ،یک به یک نیست، چون  به ازای دو \( \Large x \) یک \( \Large y \) داریم.

\( \LARGE (-1,1),(1,1) \)

تشخیص یک به یک بودن یک نابع از روی نمودار

برای تشخیص یک به یک بودن یک تابع از روی نمودار آن کافیست هر خطی که موازی محور \( \Large x \)ها رسم می‌کنیم یا نمودار را قطع نکند یا فقط در یک نقطه قطع کند تا، تابع یک تابع  یک به یک باشد در غیر اینصورت یک به یک نیست.

در مثال بالا قسمت الف اگر خطی موازی محور \( \Large x \)ها رسم کنیم نمودار را در دو نقطه قطع می‌کند ولی در قسمت ب هیچ خطی وجود ندارد که موازی محور \( \Large x \)ها رسم شود و در بیش از یک نقطه نمودار را قطع کند.

مثال ۴: جدول زیر دمای شهر تهران را در بعضی از ساعت‌های سفر نشان می‌دهد. آیا این رابطه یک یک به یک را نشان می‌دهد؟

حل ۴: این مثال یک تابع است ولی یک به یک نیست.

مثال ۵: در تابع زیر را طوری تعیین کنید، که \( \Large a,b \)  یک به یک باشد؟

\( \LARGE f=\{(7,3),(a-b,4),(a+b,3),(3,4)\} \)

جواب ۵: بابد به ازای هر \( \Large x \) یک \( \Large y \) باشد، پس باید:

\( \LARGE a-b=3 \)

\( \LARGE a+b=7 \)

\( \LARGE a=5,b=2 \)

نکته: توابع خطی به غیر از توابع خطی ثابت \( \Large (y=b) \) یک به یک هستند.

نکته: توابع سهمی و قدرمطلق ساده در بزرگترین دامنه خود یک به یک نیستند.

تشخیص یک به یک بودن تابع از روی ضابطه آن

اگر ضابطه یک تابع را داشته باشیم و بخواهیم یک به یک بودن آن را بررسی کنیم دو نقطه \( \Large (x_1 , y_1) \) و
\( \Large (x_2 , y_2) \) از این تابع را در نظر می‌گیریم. سپس \( \Large y_1 = y_2 \) قرار داده اگر بتوانیم نتیجه بگیریم \( \Large x_1 = x_2 \) یعنی یک به یک است در غیر اینصورت یک به یک نیست. یعنی داریم:

\( \LARGE f(x_1)=f(x_2) \rightarrow x_1 = x_2 \)

مثال ۶: آیا تابع \( \Large y=x^3+1 \) یک به یک است؟

حل ۶:

\( \LARGE \begin{cases} y_1=x_1 ^3 +1 \\ y_2=x_2 ^3 +1 \end{cases}  \)

\( \LARGE f(x_1)=f(x_2)  \)

\( \LARGE x_1 ^3 +1 =x_2 ^3 +1 \)

\( \LARGE x_1 ^3 =x_2 ^3 \rightarrow x_1  =x_2  \)

هر عدد یک ریشه سوم دارد پس این یک به یک است.

مثال ۷: آیا تابع \( \Large y=2x^2-3 \) یک به یک است؟

حل ۷:

\( \LARGE \begin{cases} y_1=2x_1 ^2 -3 \\ y_2=2x_2 ^2 -3 \end{cases}  \)

\( \LARGE f(x_1)=f(x_2)  \)

\( \LARGE 2x_1 ^2 -3 =2x_2 ^2 -3 \)

\( \LARGE 2x_1 ^2 =2x_2 ^2   \)

\( \LARGE x_1 ^2 =x_2 ^2   \)

\( \LARGE x_1  =\pm x_2   \)

چون هر عدد دو ریشه دوم دارد در این مثال یک به یک نیست.

تبدیل یک تابع غیر یک به یک به تابع یک به یک

مثال ۸: آیا تابع \( \Large y=x^2+1 \) با دامنه \( \Large \mathbb{R} \) یک تابع است؟

حل ۸:

اگر نمودار این تابع را رسم کنید به صورت زیر است:

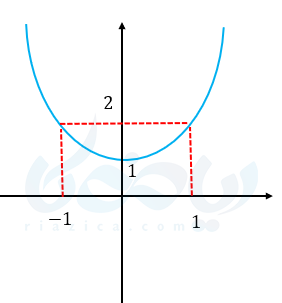
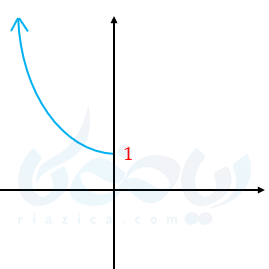
همانطور که می‌بینید این تابع در بزرگترین دامنه خود یعنی اعداد حقیقی یک به یک نیست اما با محدود کردن دامنه می‌توان این تایع را به یک تابع یک به یک تبدیل کنیم. یعنی تابع را با دامنه \( \Large (-\infty , 0] \) در نظر بگیریم در این صورت نمودار به شکل زیر می‌شود.

یا دامنه را به صورت \( \Large [0,+\infty) \) در نظر بگیریم.

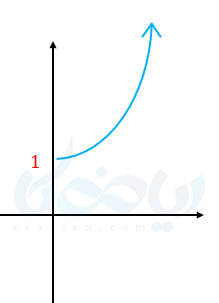
در هر دو صورت تابع به صورت یک تابع یک به یک در می‌آید.

پس می‌توان با محدود کردن دامنه یک تابع غیر یک به یک آن را به یک تابع یک به یک تبدیل کرد.

مثال ۹: آیا تابع \( \Large y=-|x+2|+1 \) یک به یک است؟ اگر جواب منفی است با محدود کردن دامنه آن را به یک تابع یک به یک تبدیل کنید.

حل ۹: چگونگی رسم این تابع را در پست تابع قدرمطلق برایتان توضیح داده‌ایم.

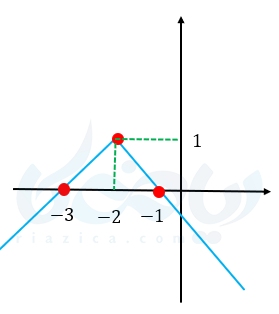
یک به یک نیست اما اگر از راس نصف نمودار را پاک کنیم یک به یک خواهد بود یعنی یا دامنه را به صورت \( \Large (-\infty,-2] \) یا \( \Large [-2,+\infty) \) در نظر بگیریم تا یک به یک شود.

استفاده از مثال نقص برای تشخیص یک به یک بودن تابع

گاهی استفاده از روش بالا برای تشخیص یک به یک بودن کاری سخت وزمانبر است می‌توان در این موارد از رسم نمودار یا زدن مثال نقص برای رد یک به یک بودن استفاده کنیم.

مثال ۱۰: آیا تابع \( \Large y=x^2+x \) یک به یک است؟

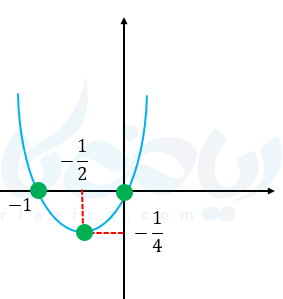
حل ۱۰:

\( \LARGE x_s = -\frac{b}{2a} = -\frac{1}{2}  \)

\( \LARGE y_s =-\frac{1}{4}    \)

همانطور که می‌بینید نمودار این تابع سهمی است که یک به یک نیست یعنی از رسم نمودار استفاده کردیم.

راه دیگر یک مقدار مثلا صفر به \( \Large y \) بدهیم و مقدار را بیابیم. اگر:

\( \LARGE x^2+x=0 \rightarrow x(x+1)=0    \)

\( \LARGE \begin{cases} x=0 \\ x=-1 \end{cases}  \)

به ازای یک \( \Large y \) دو \( \Large x \) داریم پس این  یک به یک نیست.

نکته: البته اگر معادله درجه دوم یک ریشه داشته باشد چون آن ریشه مضاعف است یک به یک نیست.

مثال ۱۱: آیا تابع \( \Large y=x^3-x \) یک به یک است؟

حل ۱۱:

اگر در این تابع \( \Large f(1) \) و \( \Large f(-1) \) را پیدا کنیم:

\( \LARGE f(1)=1^3-1=0   \)

\( \LARGE f(-1)=(-1)^3-(-1)=0   \)

پس داریم \( \Large (-1,0) \) و \( \Large (1,0) \) یعنی یک به یک نیست. با زدن مثال نقض به این نتیجه رسیدیم.

نکته: توابع اکیدا صعودی و اکیدا نزولی که در پست مربوط به پایه دوازدهم مطالعه خواهید کرد جزو توابع یک به یک هستند.

توصیه میشه در ادامه پست وارون تابع ریاضی یازدهم تجربی را مطالعه کنید.

کلام آخر

در این پست  از ریاضی یازدهم تجربی تعریف ساده این نوع تابع، یعنی اینکه به ازای هر \( \Large x \) فقط یک \( \Large y \) و به ازای هر \( \Large y \) فقط یک \( \Large x \) داریم.

دوستان ریاضیکا هر سوالی از این مبحث داشتید برایمان در قسمت دیدگاه بنویسید. کارشناسان ریاضیکا حتما به سوالاتتان پاسخ می‌دهند.