توابع صعودی و نزولی 👣📈 – گام به گام با تصویر

در این درسنامه ابتدا توابع چند جمله ای را بررسی می‌کنیم. سپس به بررسی تابع درجه 3 به عنوان یک حالت خاص از توابع چند جمله ای می‌پردازیم. در انتها نیز در مورد توابع صعودی و نزولی ، تابع اکیدا نزولی و تابع اکیدا صعودی بحث خواهیم کرد.

توابع چند جمله ای

اگر \(\Large  f(x)\) به شکل \(\Large a_nx^n+a_{n-1}x^{n-1}+\dots+a_0 \) باشد. که در آن \(\Large  a_0,a_1,\dots,a_n \) اعداد حقیقی، \(\Large  n\) یک عدد صحیح نامنفی و \(\Large  a_n\neq 0 \) است، به \(\Large  f(x)\) تابع چند جمله ای از درجۀ \(\Large  n \) می‌گوییم.

مثال 1: در درسنامۀ تابع خطی با تابع خطی آشنا شدید. همان طور که به خاطر دارید، توابعی به شکل \(\Large  f(x)=ax+b \) را توابع خطی می‌نامیم. با توجه به تعریف تابع چند جمله ای، توابع خطی توابع چند جمله ای از درجۀ یک هستند. تابع ثابت نیز که به فرم \(\Large  f(x)=b \) است، تابع چند جمله ای درجه صفر است. (در صورتی که نیاز به مرور مبحث تابع ثابت دارید، به درسنامۀ تابع ثابت مراجعه کنید). در شکل زیر نیز، نمودار یک تابع چند جمله ای از درجۀ 5 و با ضابطۀ \(\Large  f(x)=x^5+2x^4+1 \) را مشاهده می‌کنید.

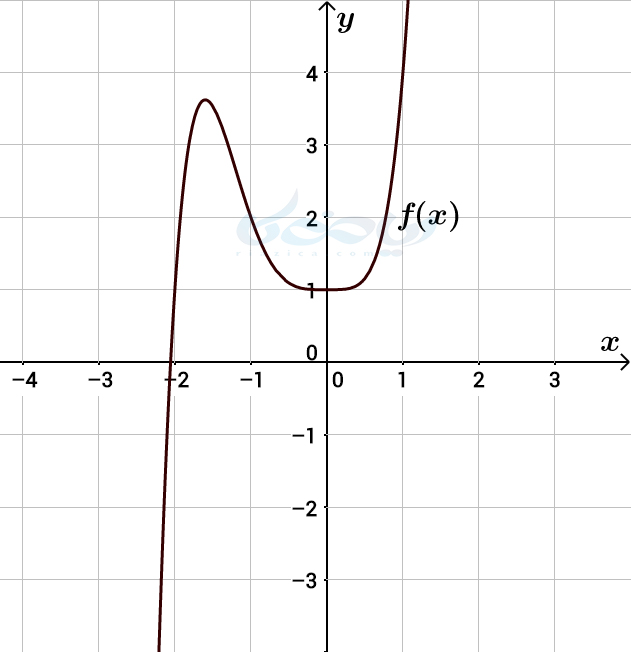
تابع درجه 3

 طبق تعریف تابع چند جمله ای که در قسمت قبل دیدید. تابع با ضابطۀ \(\Large  f(x)=ax^3+bx^2+cx+d \) را که در آن \(\Large  a\neq 0 \) است، تابع چند جمله ای از درجۀ 3 یا به اختصار تابع درجه 3 می‌نامیم. دامنه و برد تابع درجه 3 مجموعۀ اعداد حقیقی است. اگر نمودار تابع درجه 3 با ضابطۀ \(\Large  f(x)=x^3 \) را با استفاده از نقطه یابی رسم کنیم، شکل زیر به دست می‌آید:

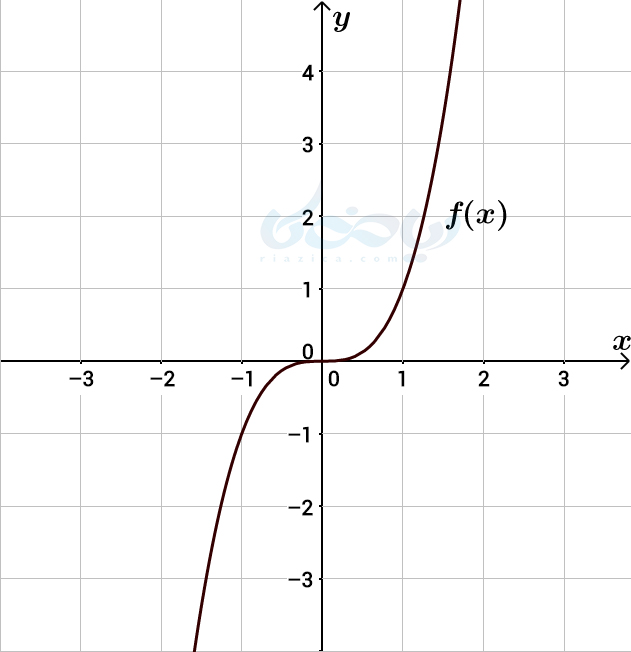
مثال 2: با استفاده از نمودار تابع \(\Large  f(x)=x^3 \)، نمودار تابع \(\Large  g(x)=(x+2)^3-1 \) را رسم کنید. دامنه و برد تابع \(\Large  g(x) \) را به دست آورید.

حل 2: در درسنامۀ رسم سهمی به روش انتقال، روش رسم چنین نمودارهایی را آموخته‌اید. همان طور که از ضابطۀ تابع \(\Large  g(x) \) پیداست، باید نمودار تابع \(\Large  f(x)=x^3 \) را 2 واحد به سمت چپ و 1 واحد به سمت پایین انتقال دهیم. به این ترتیب، نمودار تابع \(\Large g(x) \) به صورت زیر خواهد شد:

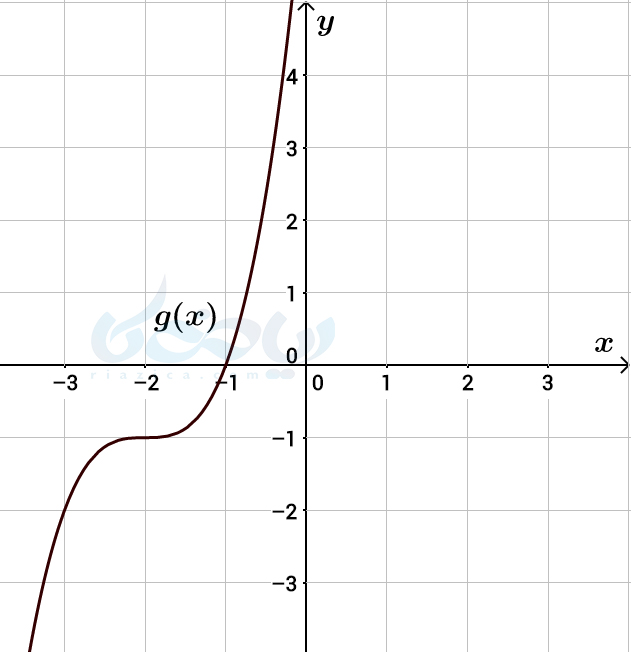
محدودیتی برای \(\Large  x \) نداریم، بنابراین دامنۀ تابع \(\Large  g(x) \) مانند تابع \(\Large  f(x) \) برابر با \(\Large  \mathbb{R} \) است. از طرفی اگر \(\Large  x \) از \(\Large  -\infty \) تا \(\Large +\infty \) تغییر کند، \(\Large  g(x) \) نیز بین \(\Large  -\infty \) تا \(\Large  +\infty \) خواهد بود. بنابراین برد \(\Large  g(x) \) نیز مانند برد \(\Large  f(x) \) برابر با مجموعۀ اعداد حقیقی است.

توابع صعودی و نزولی

پیش از این با توابع مختلفی سر و کار داشته‌اید که در برخی از بازه‌ها دارای روند کاهشی یا افزایشی بوده‌اند. در این قسمت می‌خواهیم این موضوع را به صورت دقیق تر بررسی کرده. سپس برای چهار حالتی که ممکن است با آن رو‌به‌رو شویم، نام گذاری کنیم.

اگر برای هر دو نقطۀ دلخواه \(\Large  x_1 \) و \(\Large  x_2 \) از دامنۀ تابع \(\Large  f(x) \) که \(\Large  x_1 < x_2 \)، داشته باشیم \(\Large  f(x_1)\leq f(x_2) \) آنگاه می‌گوییم \(\Large  f \) تابعی صعودی است. به بیان ساده‌تر، تابع صعودی تابعی است که با افزایش  \(\Large  y \)، \(\Large  x \)ها یا افزایش پیدا کنند و یا ثابت بمانند. در شکل زیر یک نمونه تابع صعودی را مشاهده می کنید.

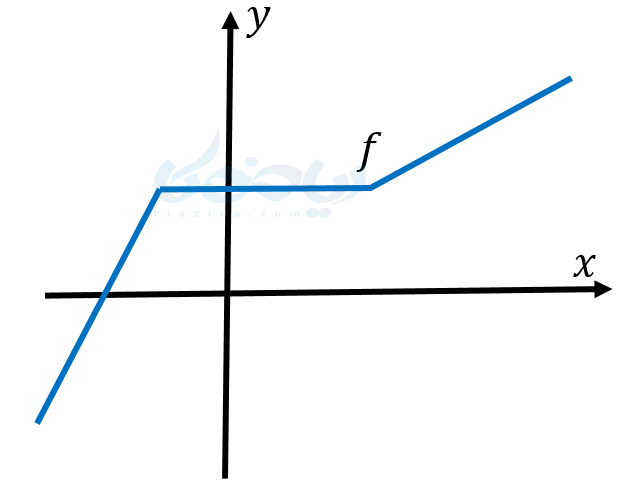
اگر برای هر دو نقطۀ دلخواه \(\Large  x_1 \) و \(\Large  x_2 \) از دامنۀ تابع \(\Large  f(x) \) که \(\Large  x_1 < x_2 \)، داشته باشیم \(\Large  f(x_1)\geq f(x_2) \) آنگاه می‌گوییم \(\Large  f \) تابعی نزولی است. به بیان ساده‌تر، تابع نزولی تابعی است که با افزایش  \(\Large  y \)، \(\Large  x \)ها یا کاهش پیدا کنند و یا ثابت بمانند. در شکل زیر یک نمونه تابع نزولی را مشاهده می کنید.

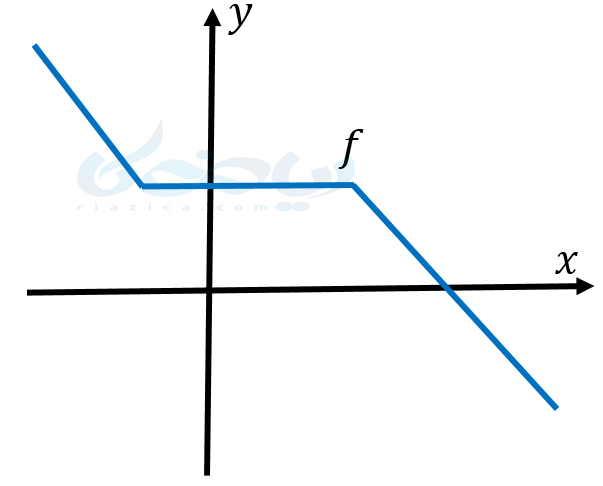
اگر برای هر دو نقطۀ دلخواه \(\Large  x_1 \) و \(\Large  x_2 \) از دامنۀ تابع \(\Large  f(x) \) که \(\Large  x_1 < x_2 \)، داشته باشیم \(\Large  f(x_1)< f(x_2) \) آنگاه می‌گوییم \(\Large  f \) تابعی اکیدا صعودی است. به بیان ساده‌تر، تابع اکیدا صعودی تابعی است که با افزایش  \(\Large  y \)، \(\Large  x \)ها فقط افزایش پیدا کنند. در شکل زیر یک نمونه تابع اکیدا صعودی را مشاهده می کنید.

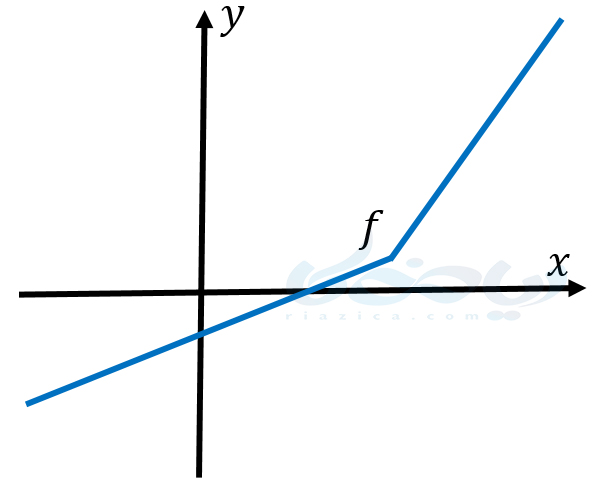
اگر برای هر دو نقطۀ دلخواه \(\Large  x_1 \) و \(\Large  x_2 \) از دامنۀ تابع \(\Large  f(x) \) که \(\Large  x_1 < x_2 \)، داشته باشیم \(\Large  f(x_1)> f(x_2) \) آنگاه می‌گوییم \(\Large  f \) تابعی اکیدا نزولی است. به بیان ساده‌تر، تابع اکیدا نزولی تابعی است که با افزایش  \(\Large  y \)، \(\Large  x \)ها فقط کاهش پیدا کنند. در شکل زیر یک نمونه تابع اکیدا نزولی را مشاهده می کنید.

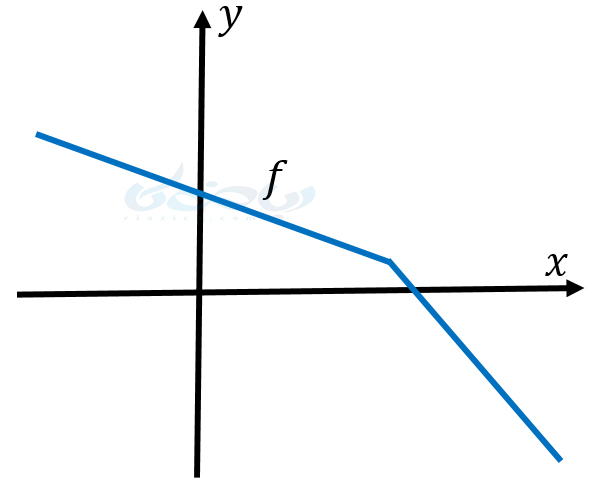
مثال از توابع صعودی و توابع نزولی

ممکن است وضعیت یک تابع در بازه های مختلف دامنه متفاوت باشد. به مثال 3 دقت کنید.

مثال 3: نمودار تابع \(\Large  f(x) \) در شکل زیر رسم شده است. تابع \(\Large f \) در کدام بازه اکیداٌ صعودی و در کدام بازه اکیدا نزولی است؟

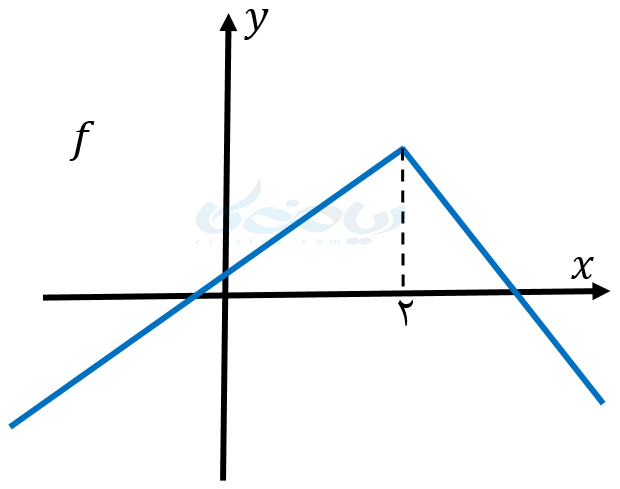
حل 3: همان طور که از نمودار پیداست، تابع \(\Large  f \) در بازۀ \(\Large  (-\infty,2] \) اکیدا صعودی و در بازۀ \(\Large  [2,+\infty) \) اکیدا نزولی است.

مثال 4: تابع \(\Large  f(x)=x^2|x| \) در کدام بازه نزولی و در کدام بازه صعودی است؟

حل 4: می‌توانیم با استفاده از تعیین علامت تابع، آن را به صورت یک تابع چند ضابطه‌ای نوشته و سپس نمودار را رسم کنیم. قدر مطلق \(\Large x \) به ازای \(\Large  x \) های مثبت، برابر با \(\Large  +x\) است و به ازای \(\Large  x\) های منفی، برابر با \(\Large  -x\) است. بنابراین \(\Large  f(x) \) را می‌توانیم به صورت زیر بنویسیم:

\(\LARGE  f(x)=\begin{cases}  x^3 \quad &x>0 \\ -x^3 \quad &x<0 \\ \end{cases} \)

بنابراین باید در نیمۀ سمت راست محور \(\Large x \)، نیمۀ سمت راست تابع درجه سوم \(\Large  g(x)=x^3 \) را رسم کرده و در نیمۀ سمت چپ محور \(\Large  x \)، قرینۀ نیمۀ سمت چپ تابع درجه سوم \(\Large  g(x)=x^3 \) را رسم کنیم. با انجام این کار، نمودار \(\Large  f(x) \) به شکل زیر در می‌آید:

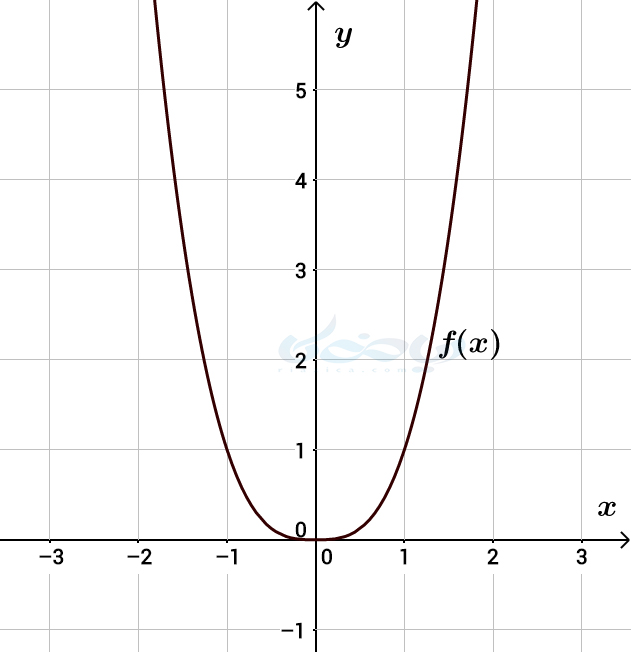
همان طور که از نمودار \(\Large  f(x) \) پیداست، تابع در بازۀ \(\Large  (-\infty,0] \) اکیدا نزولی و در بازۀ \(\Large  [0,+\infty) \) اکیدا صعودی است.

مثال 5: تابعی اکیدا صعودی یا اکیدا نزولی مثال بزنید که یک به یک نباشد.

حل 5: این کار امکان پذیر نیست. برای اینکه یک تابع یک به یک نباشد، باید \(\Large  x_1 \) و \(\Large  x_2 \) در دامنۀ \(\Large  f(x) \) موجود باشد که \(\Large  x_1 \neq x_2 \) اما \(\Large  f(x_1)=f(x_2) \) باشد. این در حالی است که در تابع اکیدا صعودی یا اکیدا نزولی، اگر \(\Large  x_1 \neq x_2 \) باشد آنگاه یا  \(\Large  x_1 < x_2\) یا \(\Large  x_1 > x_2 \) است. در نتیجه بسته به اکیدا صعودی بودن یا اکیدا نزولی بودن تابع، یا \(\Large  f(x_1)<f(x_2) \) و یا \(\Large  f(x_1)>f(x_2) \) خواهد بود. بنابراین هیچ گاه \(\Large  f(x_1)=f(x_2) \) نخواهد شد.

در ادامه پست ترکیب توابع ریاضی دوازدهم تجربی را مطالعه کنید.

زنگ آخر کلاس توابع صعودی و نزولی – توابع چند جمله ای

در این درسنامه ابتدا توابع چند جمله ای را معرفی کردیم. همان طور که گفتیم، توابع ثابت و توابع خطی مثال‌هایی از توابع چند جمله ای هستند. در ادامه به بررسی تابع درجه 3 با جزئیات بیشتر پرداختیم. در انتها نیز توابع صعودی و نزولی را معرفی کردیم. همان طور که دیدید برخی از توابع، صعودی، برخی نزولی، برخی صعودی اکید و برخی نزولی اکید هستند. در این بین توابعی هم هستند که در هیچ یک از این چهار گروه نمی گنجند، اما همان طور که دیدیم در برخی از موارد می‌توان بازه های مختلف یک تابع را از این منظر بررسی کرد.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث توابع توابع صعودی و نزولی – توابع چند جمله ای دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.