آموزش ریاضی پایه دوازدهم تجربی
ترکیب توابع ریاضی دوازدهم تجربی ⚙️📚 – همان آموزشی که دنبالش بودید!
در این درسنامه به مبحث ترکیب توابع ریاضی دوازدهم تجربی میپردازیم. ابتدا مثالی را میبینیم تا با مفهوم ترکیب توابع آشنا شویم. سپس، مراحل ساخت تابع مرکب را بیان میکنیم. در نهایت در مورد دامنۀ تابع مرکب و نحوۀ به دست آوردن ضابطۀ آن بحث خواهیم کرد.
مفهوم ترکیب توابع
برای روشن شدن مبحث ترکیب توابع ریاضی دوازدهم تجربی ابتدا بهتر است با ذکر یک مثال، مفهوم ترکیب توابع را معرفی کنیم.
مثال 1: میدانیم که ماندگاری کووید 19 با افزایش دما کاهش مییابد. فرض کنید رابطۀ ماندگاری این ویروس بر روی لباس برای دماهای بالای صفر، به صورت \(\Large S(t)=\frac{30}{t+1}\) باشد. در آن \(\Large S\) ماندگاری ویروس بر حسب ساعت و \(\Large t\) دما بر حسب درجۀ سانتی گراد است. حال فرض کنید این ویروس روی لباس یک نفر وجود دارد. احتمال ابتلای این فرد به ویروس از رابطۀ \(\Large I(s)=\frac{s+1}{s+2}\) به دست میآید. در آن \(\Large I\) احتمال ابتلای فرد و \(\Large s\) ماندگاری ویروس بر روی لباس بر حسب ساعت است. اگر دمای هوا \(\Large 29\) درجۀ سانتی گراد باشد، احتمال ابتلای این فرد چه قدر است؟
حل ۱: اگر دمای هوا \(\Large 29\) درجۀ سانتی گراد باشد. ماندگاری ویروس روی لباس بر حسب ساعت برابر است با:
\(\LARGE S(29)=\frac{30}{29+1}=1\)
بنابراین احتمال ابتلای این فرد به ویروس برابر خواهد بود با:
\(\LARGE I(1)=\frac{1+1}{1+2}=\frac{2}{3}\)
بیایید حلمان را مرور کنیم. اگر به توابع \(\Large S\) و \(\Large I\) به شکل دو ماشین نگاه کنیم. ابتدا خروجی \(\Large S\) را به ازای ورودی \(\Large t=29\) حساب کردیم. سپس، همین خروجی را به عنوان ورودی به \(\Large I\) دادیم. خروجی \(\Large I\) را محاسبه کردیم. میتوانید این فرآیند را در شکل زیر نیز مشاهده کنید.

این مثال کمک زیادی به درک ما از ترکیب توابع خواهد کرد.
ساخت تابع مرکب
به مثال 1 و حل آن دقت کنید. آیا میتوانیم به جای اینکه خروجی را در دو مرحله به دست آوریم. این کار را در یک مرحله انجام دهیم؟ یعنی دو تابع \(\Large S\) و \(\Large I\) را به گونهای ترکیب کرده و یک تابع جدید بسازیم. سپس، بدون محاسبۀ خروجی توابع \(\Large S\) و \(\Large I\) به صورت جداگانه، خروجی تابع جدید را محاسبه کرده و جواب را به دست آوریم. پاسخ سوال ما مثبت است. برای اینکه بهتر متوجه شوید، به مثال زیر دقت کنید. این مثال مقدمهای خواهد بود بر تعریف ترکیب توابع که در ادمه میبینیم.
مثال 2: در مثال 1، احتمال ابتلای فردا را در دمای 29 درجۀ سانتی گراد به دست آوردیم. اگر دمای هوا \(\Large x\) درجۀ سانتی گراد باشد، احتمال ابتلای فرد چه قدر است؟
حل ۲: اگر دمای هوا \(\Large x\) درجۀ سانتی گراد باشد. ماندگاری ویروس روی لباس بر حسب ساعت برابر است با:
\(\LARGE S(x)=\frac{30}{x+1}\)
بنابراین احتمال ابتلای این فرد به ویروس برابر خواهد بود با:
\(\LARGE I(1)=\frac{\frac{30}{x+1}+1}{\frac{30}{x+1}+2}=\frac{x+31}{2x+32}\)
بسیار عالی شد! این بار احتمال ابتلای فرد در دمای \(\Large x\) درجه را به دست آوردیم. بنابراین اگر احتمال ابتلای فرد در هر دمای دیگری را خواستیم. کافی است دما را در رابطۀ \(\Large \frac{x+31}{2x+32}\) به جای \(\Large x\) جایگذاری کنیم. دیگر نیازی به محاسبۀ خروجی توابع \(\Large S\) و \(\Large I\) به صورت جداگانه نیست. در واقع با این کار، توابع \(\Large S\) و \(\Large I\) را ترکیب کرده و تابعی با ضابطۀ \(\Large \frac{x+31}{2x+32}\) به دست آوردیم. به عبارت دیگر، همان طور که در مثال قبل گفتیم، خروجی تابع \(\Large S\) را به عنوان ورودی به تابع \(\Large I\) داده و ترکیبی از این دو تابع ساختیم. شکل زیر، مراحلی را که در این مساله طی کردیم به خوبی نشان میدهد.
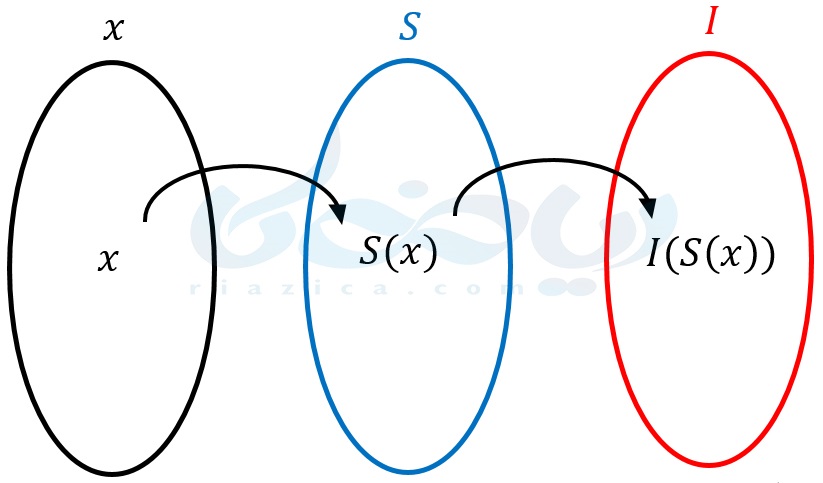
تعریف تابع مرکب
مثالهای 1 و 2 شهود خوبی از مفهوم ترکیب توابع ریاضی دوازدهم تجربی به ما دادند. اینک میخواهیم تابع مرکب را به صورت دقیقتر تعریف کنیم.
تعریف: توابع \(\Large f\) و \(\Large g\) را در نظر بگیرید. اگر اشتراک برد \(\Large g\) و دامنۀ \(\Large f\) ناتهی باشد، تابع \(\Large f(g(x))\) را تابع مرکب گفته و آن را به صورت \(\Large fog\) نمایش میدهیم.
ممکن است در تعریف بالا یک نکته مبهم باشد. چه لزومی دارد اشتراک برد \(\Large g\) و دامنۀ \(\Large f\) ناتهی باشد؟ مثالی که در ادامه خواهید دید، لزوم وجود این شرط را به روشنی نشان میدهد.
مثال 3: اگر \(\Large g(x)=1\) و \(\Large f(x)=\frac{1}{x-1}\) باشد، تابع مرکب \(\Large fog\) را به دست آورید.
حل ۳: برای به دست آوردن تابع مرکب \(\Large fog\) باید خروجی تابع \(\Large g\) را به عنوان ورودی به تابع \(\Large f\) بدهیم. تابع \(\Large g\) تابع ثابت و خروجی آن همیشه عدد \(\Large 1\) است. بنابراین اگر خروجی \(\Large g\) را به عنوان ورودی به \(\Large f\) دهیم، خواهیم داشت:
\(\LARGE f(g(x))=f(1)\)
اما \(\Large f(1)\) وجود ندارد زیرا در مخرج نمیتوانیم صفر داشته باشیم. بنابراین تابع مرکب \(\Large f(g(x))\) وجود ندارد. به عبارت دیگر، برد تابع \(\Large g\) برابر با \(\Large \{1\}\) و دامنۀ تابع \(\Large f\) برابر با \(\Large \mathbb{R}-\{1\}\) است. بنابراین برد \(\Large g\) و دامنۀ \(\Large f\) هیچ اشتراکی ندارند و نمیتوان تابع مرکب \(\Large fog\) ساخت.
دامنۀ تابع مرکب
با توجه به نکتهای که در حل مثال 3 گفتیم، میتوان دامنۀ تابع مرکب را به دست آورد. دامنۀ تابع مرکب \(\Large fog\) متشکل از \(\Large x\)هایی است که در هر دو شرط زیر صدق کنند:
- \(\Large x\) در دامنۀ \(\Large g\) باشد.
- \(\Large g(x)\) در دامنۀ \(\Large f\) باشد.
نکتۀ حائز اهمیت در ترکیب توابع این است که نمیتوان دامنۀ تابع مرکب را از روی ضابطۀ آن تشخیص داد. برای به دست آوردن دامنۀ تابع مرکب باید حتما دو شرط بالا را بررسی کنیم. در مثال بعد خواهیم دید که محاسبۀ دامنۀ تابع مرکب از روی تعریف و از روی ضابطه، به دو نتیجۀ متفاوت میانجامد و همان طور که گفتیم، نتیجهای درست است که مطابق با تعریف باشد.
مثال 4: اگر \(\Large g(x)=\sqrt{X}\) و \(\Large f(x)=x^2\) باشد، دامنۀ تابع مرکب \(\Large fog\) را به دست آورید.
حل ۴: باید \(\Large x\)هایی را پیدا کنیم که در دو شرطی که گفتیم صدق کنند. دامنۀ تابع \(\Large g\) برابر است با \(\Large [0, +\infty)\). از طرفی \(\Large g\) در دامنۀ \(\Large f\) قرار دارد، زیرا برد \(\Large g\) برابر با \(\Large [0, +\infty)\) و دامنۀ \(\Large f\) برابر با \(\Large \mathbb{R}\) است. در نتیجه دامنۀ \(\Large fog\) برابر است با \(\Large [0, +\infty)\). اگر میخواستیم دامنه را از روی ضابطۀ تابع مرکب تعیین کنیم، دچار اشتباه میشدیم، زیرا ضابطۀ تابع مرکب \(\Large fog\) برابر است با:
\(\LARGE f(g(x))=(\sqrt{x})^2=x\)
دامنۀ تابعی با ضابطۀ بالا برابر با \(\Large \mathbb{R}\) است، اما همان طور که دیدیم تنها \(\Large x\)های بزرگتر یا مساوی صفر در دامنۀ \(\Large fog\) صدق میکنند. در نتیجه برای تعیین دامنۀ تابع مرکب نمیتوان از ضابطۀ آن استفاده کرد.
مثالهایی از ترکیب توابع
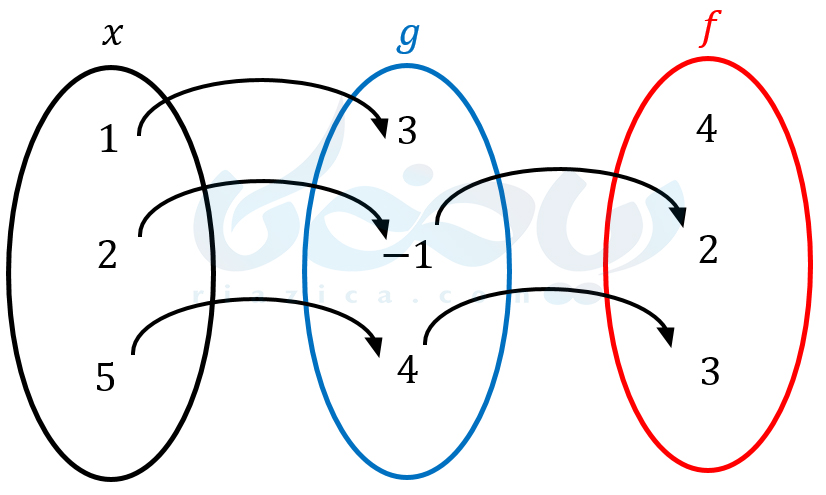
مثال 5: اگر \(\Large g=\{(1, 3), (2, -1), (5, 4)\}\) و \(\Large f=\{(-1, 2), (4, 3), (5, 4)\}\) باشد. \(\Large fog\) را به دست آورید.
حل ۵: به زبان ساده، برای به دست آوردن \(\Large fog\) باید خروجیهای \(\Large g\) را به عنوان ورودی به \(\Large f\) داده. خروجی \(\Large f\) را به دست آوریم. با انجام این کار خواهیم داشت:
\(\LARGE f(g(x))=\{(2, 2), (5, 3)\} \)
در شکل زیر نیز میتوانید چونگی حل مساله را مشاهده کنید.
مثال 6: اگر \(\Large g=\sqrt{x-2}\) و \(\Large f=\sqrt{x^2-9}\) باشد. ضابطه و دامنۀ \(\Large fog\) را به دست آورید.
حل ۶: برای به دست آوردن ضابطۀ \(\Large fog\). کافی است \(\Large g\) را به جای \(\Large x\) در \(\Large f(x)\) قرار دهیم. بنابراین داریم:
\(\LARGE fog=\sqrt{(\sqrt{x-2})^2-9} \)
\(\LARGE =\sqrt{x-2-9} \)
\(\LARGE =\sqrt{x-11} \)
همان طور که گفتیم، برای به دست آوردن دامنۀ \(\Large fog\) نمیتوان از ضابطۀ آن استفاده کرد. باید دو شرطی را که گفتیم بررسی کنیم. دامنۀ \(\Large g\) برابر با \(\Large [2, +\infty)\) و برد آن برابر با \(\Large [0, +\infty)\) است. از طرفی برای به دست آوردن دامنۀ \(\Large f\) داریم:
\(\LARGE f(x)=\sqrt{x^2-9} \)
\(\LARGE \Rightarrow x^2 \geq 9 \)
\(\LARGE \Rightarrow x\geq 3\) یا \(\LARGE x\leq -3 \)
بنابراین دامنۀ \(\Large f\) برابر است با \(\Large (-\infty, -3] \cup [3, +\infty)\). حال باید اشتراک برد \(\Large g\) و دامنۀ \(\Large f\) را پیدا کنیم. یعنی باید بینیم به ازای چه \(\Large x\)هایی، \(\Large g(x)\) در \(\Large (-\infty, -3] \cup [3, +\infty)\) قرار دارد. از آنجاییکه \(\Large g\) بزرگتر یا مساوی صفر است، پس \(\Large g\) نمیتواند در \(\Large (-\infty, -3]\) قرار بگیرد. بنابراین باید به دنبال \(\Large x\)هایی باشیم که به ازای آنها \(\Large g(x)\) در بازۀ \(\Large [3, +\infty)\) قرار بگیرد. داریم:
\(\LARGE \sqrt{x-2}\geq 3 \)
\(\LARGE x-2 \geq 9 \)
\(\LARGE x \geq 11 \)
پس، باید هم محدودیت دامنۀ \(\Large g\) که برابر با \(\Large [2, +\infty)\) بود را در نظر بگیریم. هم محدودیت \(\Large x \geq 11\). اشتراک این دو بازه، یعنی \(\Large [2, +\infty)\cap[11, +\infty)\) دامنۀ \(\Large fog\) را به ما میدهد. پس، دامنۀ \(\Large fog\) برابر است با \(\Large [11, +\infty)\).
در ادامه توصیه میشه تایع وارون رو مطالعه کنید.
زنگ آخر کلاس ترکیب توابع ریاضی دوازدهم تجربی
در این درسنامه به بررسی مبحث ترکیب توابع ریاضی دوازدهم تجربی پرداختیم. ابتدا با ذکر یک مثال درک مناسبی از مفهوم ترکیب توابع پیدا کردیم. سپس، در مورد نحوۀ ساخت تابع مرکب و چگونگی به دست آوردن ضابطۀ آن صحبت کردیم. در ادامه به بررسی دامنۀ تابع مرکب پرداختیم. همان طور که دیدیم، دامنۀ تابع مرکب را نمیتوان با استفاده از ضابطۀ آن به دست آورد. در انتها نیز چند مثال از تابع مرکب حل کردیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث ترکیب توابع ریاضی دوازدهم تجربی دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





خیلی عالی توضیح داده بودید ممنون
سلام و عرض ادب
ممنون از انرژی و پیام پرمهرتون.
موفق باشید
عاااااااااااااالییییییییییییییی
با سلام وعرض ادب
ممنون از شما
سلام خسته نباشید
ای کاش مثل ریاضی دهم ، ریاضی یازدهم و دوازدهم رو هم به ترتیب میزاشتین که درکش بالاتر و فهم ترتیبیش بالاتر بره
سلام دوست عزیز
انشالله به زودی درست میکنیم