آموزش ریاضی پایه دوازدهم تجربی
تابع وارون ⚙️🚰 – به راحتی آب خوردن!
در این درسنامه به تابع وارون میپردازیم. ابتدا روش به دست آوردن ضابطۀ تابع وارون را با یکدیگر میبینیم. سپس در مورد محدود کردن دامنه تابع بحث میکنیم. همان طور که خواهیم دید، در توابع غیر یک به یک میتوانیم با محدود کردن دامنه تابع، وارون تابع محدود شده را به دست آوریم.
یادآوری مفهوم تابع وارون
در پایۀ یازدهم با تابع وارون آشنا شدید. همان طور که به یاد دارید، در صورتی که یک تابع یک به یک باشد، با جابهجا کردن مولفههای زوجهای مرتب آن، تابعی جدید به دست میآید. به آن تابع وارون میگوییم. (در صورتی که نمایش یک تابع به وسیلۀ زوجهای مرتب آن را فراموش کردهاید، به درسنامۀ تابع مراجعه کنید). اگر تابع \(\Large f \) یک به یک باشد، وارون آن را با \(\Large f^{-1} \) نشان میدهیم. همچنین در پایۀ یازدهم دیدید. برای رسم نمودار تابع \(\Large f^{-1} \) کافی است قرینۀ نمودار تابع \(\Large f(x) \) را نسبت به خط \(\Large y=x \) به دست آورید.
مثال از مفهوم تابع وارون
مثال 1: اگر \(\Large f=\{(2,5),(3,4),(5,1)\} \) باشد، آیا \(\Large f \) یک به یک است؟ اگر یک به یک است، \(\Large f ^{-1}(x)\) را به دست آورید. \(\Large f^{-1}(5) \) چه قدر است؟
حل: همان طور که پیداست، هیچ کدام از زوج مرتبهای \(\Large f \) مولفۀ دوم تکراری ندارند. بنابراین تابع \(\Large f \) یک به یک است. برای به دست آوردن \(\Large f^{-1} \) کافی است جای مولفههای اول و دوم زوج مرتبهای \(\Large f \) را با یکدیگر عوض کنیم. با انجام این کار، \(\Large f^{-1} \) به صورت زیر خواهد شد:
\(\Large f^{-1}=\{(5,2),(4,3),(1,5)\} \)
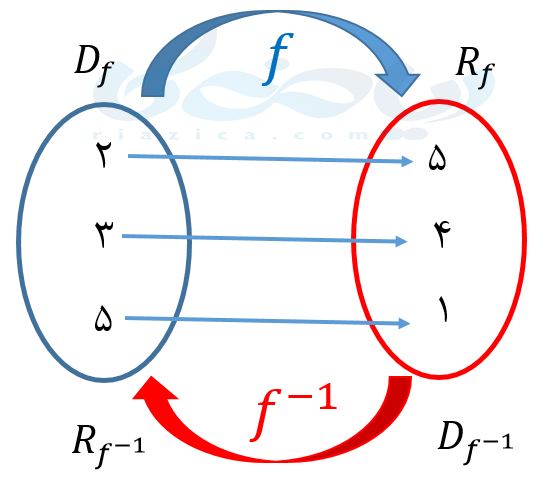
با توجه به عبارت بالا، \(\Large f^{-1}(5) \) برابر است با مولفۀ دوم زوج مرتب \(\Large (5,2) \) در تابع \(\Large f^{-1} \). بنابراین \(\Large f^{-1}(5) \) برابر است با 2. اگر دامنۀ \(\Large f \) را \(\Large D_f \) و برد \(\Large f \) را \(\Large R_f\) بنامیم، همچنین اگر دامنۀ \(\Large f^{-1} \) را \(\Large D_{f^{-1}} \) و برد \(\Large f^{-1} \) را \(\Large R_{f^{-1}}\) بنامیم، ارتباط بین \(\Large f \) و \(\Large f^{-1} \) را میتوان به صورت زیر نشان داد:
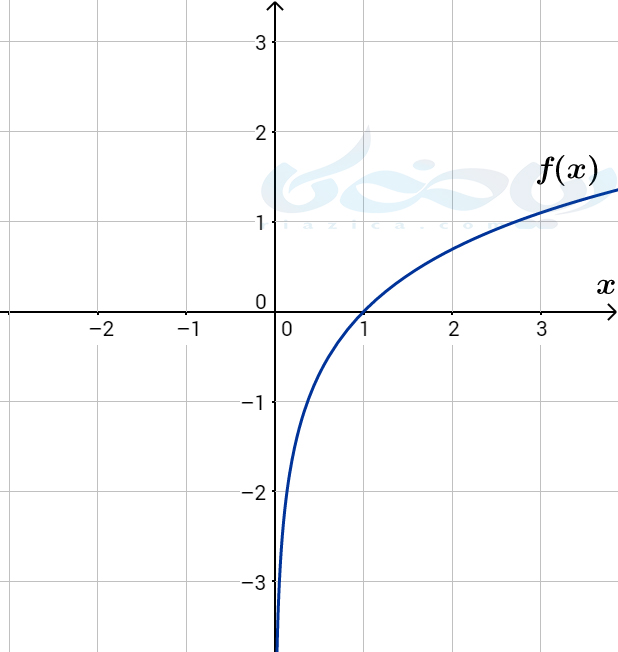
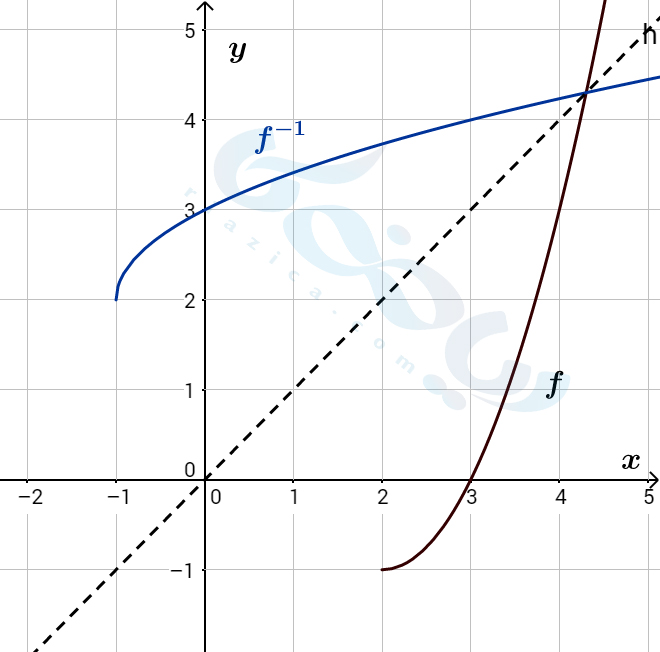
مثال 2: نمودار تابع \(\Large f(x) \) در شکل زیر رسم شده است. نمودار \(\Large f^{-1} \) را به دست آورید.
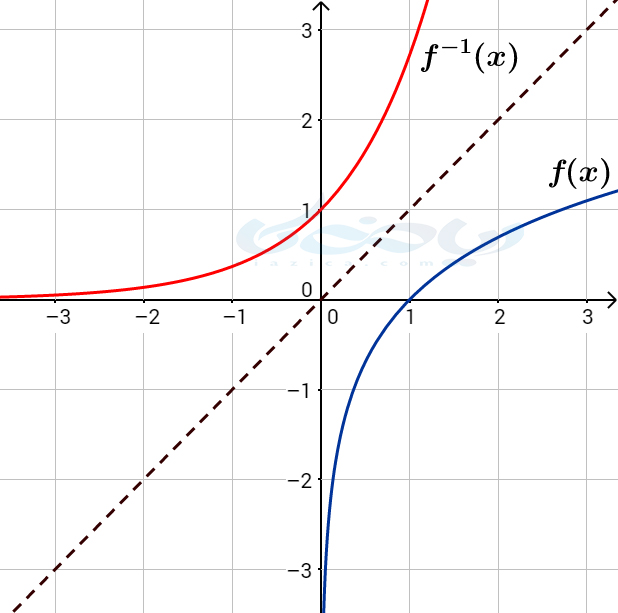
حل: همان طور که گفتیم، برای رسم نمودار \(\Large f^{-1} \) کافی است قرینۀ نمودار \(\Large f(x) \) را نسبت به خط \(\Large y=x\) به دست آوریم. با انجام این کار، نمودار \(\Large f^{-1}(x) \) به صورت زیر خواهد شد:
چه زمانی دو تابع وارون یکدیگرند؟
فرض کنید تابع \(\Large f(x) \) تابعی یک به یک بوده و دامنه و برد آن به ترتیب \(\Large D_f \) و \(\Large R_f \) باشد. واورن تابع \(\Large f(x) \)، تابع \(\Large f^{-1}(x) \) است. دامنۀ آن یعنی \(\Large D_{f^{-1}} \) برابر با \(\Large R_f \) و برد آن یعنی \(\Large R_{f^{-1}} \) برابر با \(\Large D_f \) است. برای اینکه بهتر متوجه شوید، شکل زیر را در نظر بگیرید:
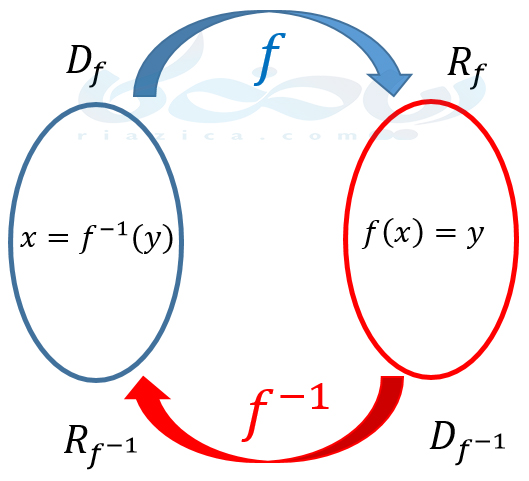
حال فرض کنید میخواهیم \(\Large f(f^{-1}(x))\) را که \(\Large x \in D_{f^{-1}} \) است به دست آوریم. برای این کار باید از \(\Large D_{f^{-1}}\) به \(\Large R_{f^{-1}} \) رفته و سپس به \(\Large R_f \) که همان \(\Large D_{f^{-1}}\) است، بازگردیم. بنابراین خواهیم داشت:
\(\LARGE f(f^{-1}(x))=x; x \in D_{f^{-1}}\)
اگر عکس این کار را انجام دهیم، یعنی \(\Large f^{-1}(f(x)) \) را که \(\Large x \in D_f \) است حساب کنیم، به نتیجۀ مشابهی میرسیم. برای محاسبۀ \(\Large f^{-1}(f(x)) \) ابتدا از \(\Large D_f \) به \(\Large R_f \) رفته و سپس از \(\Large R_f \) که همان \(\Large D_{f^{-1}} \) است، به \(\Large R_{f^{-1}} \) که همان \(\Large D_f \) است، باز میگردیم. بنابراین خواهیمداشت:
\(\LARGE f^{-1}(f(x))=x; x \in D_f \)
اگر دو تابع \(\Large f(x) \) و \(\Large g(x) \) دو شرط زیر را داشته باشند، وارون یکدیگرند:
- \(\LARGE (fog)(x)=x; x \in D_g \)
- \(\LARGE (gof)(x)=x; x \in D_f \)
مثال 3: نشان دهید دو تابع \(\Large f(x)=2x+5 \) و \(\Large g(x)=\frac{x-5}{2} \) وارون یکدیگرند.
حل:
\(\LARGE (fog)(x)=2\times \frac{x-5}{2} +5\)
\(\LARGE =x-5+5=x\)
\(\LARGE (gof)(x)=\frac{(2x+5)-5}{2} \)
\(\LARGE =\frac{2x}{2}=x\)
همان طور که دیدید، \(\Large fog(x) \) و \(\Large gof(x) \) برابر با \(\Large x \) شد. بنابراین توابع \(\Large f(x) \) و \(\Large g(x) \) وارون یکدیگر هستند.
ضابطۀ تابع معکوس
اگر \(\Large f(x) \) تابعی یک به یک باشد، برای به دست آوردن ضابطۀ \(\Large f^{-1}\) کافی است در معادلۀ \(\Large y=f(x) \) ،\(\Large x \) را بر حسب \(\Large y \) به دست آوریم. سپس، \(\Large x \) را با \(\Large y \) جابجا کرده تا ضابطۀ \(\Large f^{-1}\) به دست آید. به مثال های زیر دقت کنید.
مثال از محاسبۀ ضابطۀ تابع وارون
مثال 4: ضابطۀ وارون تابع \(\Large f(x)=2+\sqrt{4x+5}\) را به دست آورده و دامنه و برد \(\Large f^{-1} \) را مشخص کنید.
حل:
\(\LARGE y=2+\sqrt{4x+5}\)
\(\LARGE \Rightarrow \sqrt{4x+5}=y-2\)
\(\LARGE \Rightarrow 4x+5=(y-2)^2\)
\(\LARGE \Rightarrow 4x=(y-2)^2-5\)
\(\LARGE \Rightarrow x=\frac{(y-2)^2-5}{4}\)
\(\LARGE \Rightarrow f^{-1}(x)=\frac{(x-2)^2-5}{4}\)
در تابع \(\Large f(x) \) از آنجاییکه زیر رادیکال باید مثبت باشد، \(\Large D_f=[-\frac{5}{4},+\infty) \) است. از طرفی چون \(\Large \sqrt{4x+5} \) بزرگتر مساوی صفر است، \(\Large \sqrt{4x+5}+2 \) بزرگتر مساوی 2 میشود. بنابراین \(\Large R_f=[2,+\infty) \) است. دامنۀ \(\Large f^{-1} \) برابر با برد \(\Large f \) و برد \(\Large f^{-1} \) برابر با دامنۀ \(\Large f \) است. لذا دامنه و برد \(\Large f^{-1} \) برابر است با:
\(\LARGE D_{f^{-1}}=[2,+\infty) \)
\(\LARGE R_{f^{-1}}=[-\frac{5}{4},+\infty) \)
محدود کردن دامنه تابع
همان طور که در پایۀ یازدهم خواندید، توابعی که یک به یک نباشند وارون ندارند. اما در صورتی که دامنۀ یک تابع غیر یک به یک را محدود به یک بازه یا زیرمجموعۀ خاص کنیم، میتوانیم تابعی یک به یک به دست آوریم. مثلا، تابع \(\Large f(x)=|x| \) که نمودار آن در شکل زیر رسم شده است، یک به یک نیست.
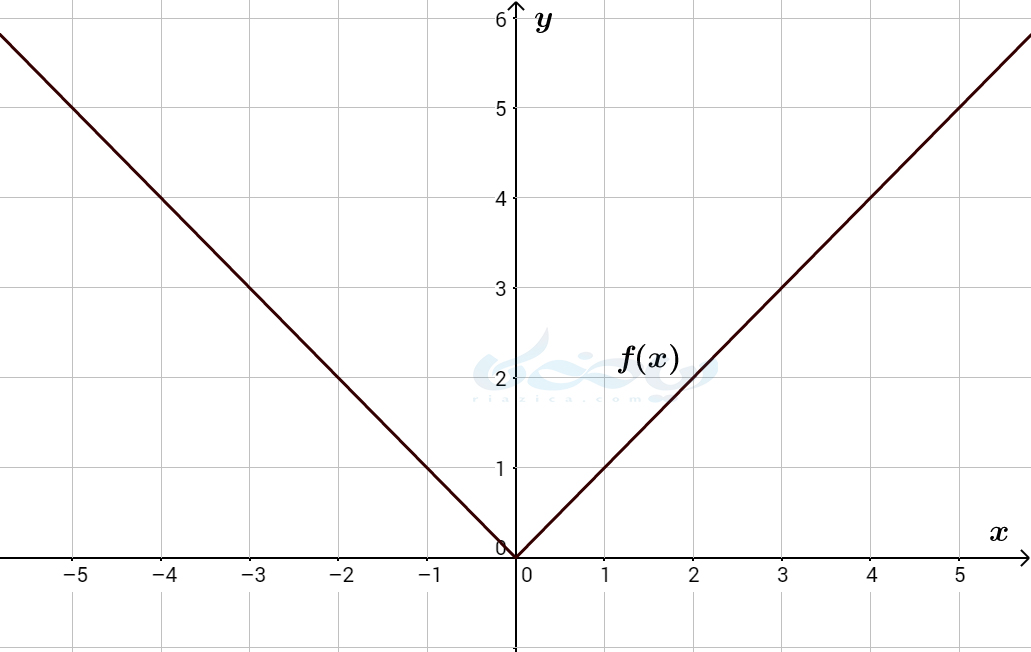
اما اگر دامنۀ \(\Large f(x) \) را به \(\Large (-\infty,0] \) یا به \(\Large [0,+\infty) \) و یا زیرمجموعهای از این دو بازه محدود کنیم، تابع یک به یک خواهد شد. در نتیجه میتوانیم معکوس تابع با دامنۀ جدید را محاسبه کنیم. مثلا، در شکل زیر دامنۀ تابع \(\Large f(x)=|x|\) را به بازۀ \(\Large (-\infty,-1]\) محدود کرده و قرینۀ آن را نسبت به خط \(\Large y=x\) رسم کردیم. در نتیجه نمودار \(\Large f^{-1}\) برای تابع با دامنۀ محدود شده به دست آمد.
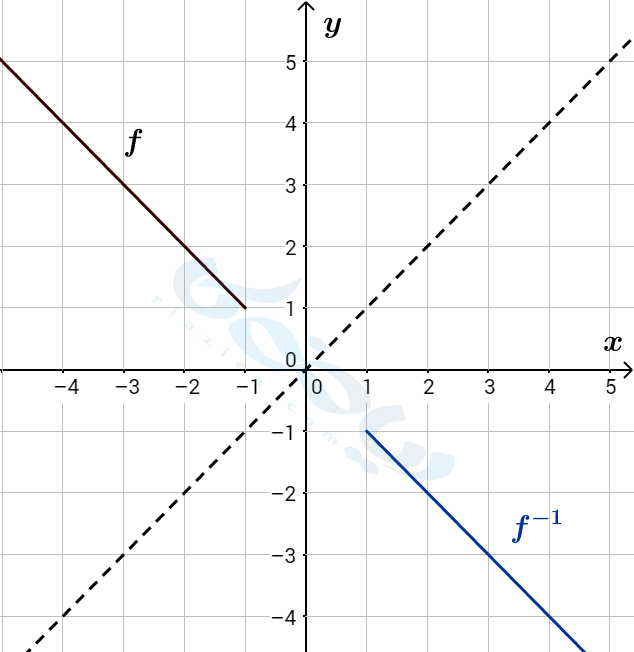
مثال از محدود کردن دامنه تابع
مثال 5: نمودار تابع \(\Large f(x)=x^2-4x+3 \) در شکل زیر رسم شده است. دامنۀ تابع را به گونهای محدود کنید که تابع یک به یک به دست آید. سپس، وارون آن را محاسبه کنید.
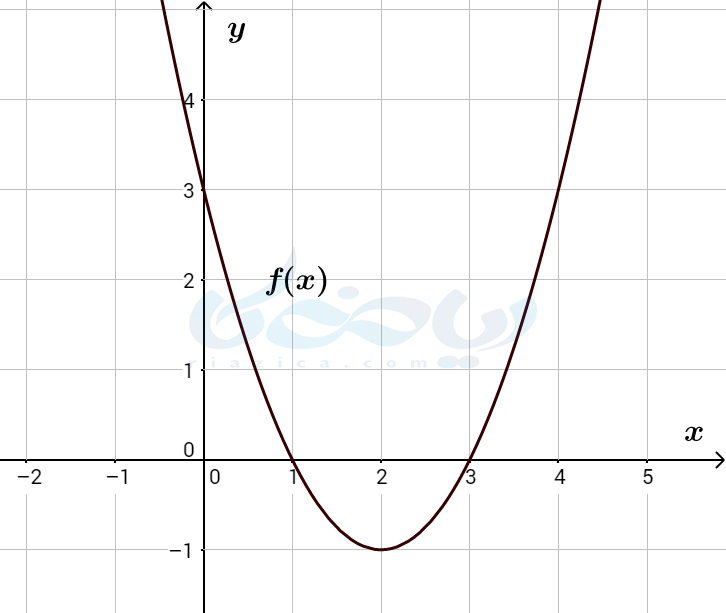
حل: این مثال پاسخ یکتا ندارد. به روشهای مختلفی میتوان دامنۀ تابع را محدود کرده و تابعی یک به یک به دست آورد. به طور مثال میتوانیم دامنۀ تابع را به بازۀ \(\Large [2,+\infty) \) محدود کنیم. در این صورت نمودار تابع به صورت زیر در میآید:
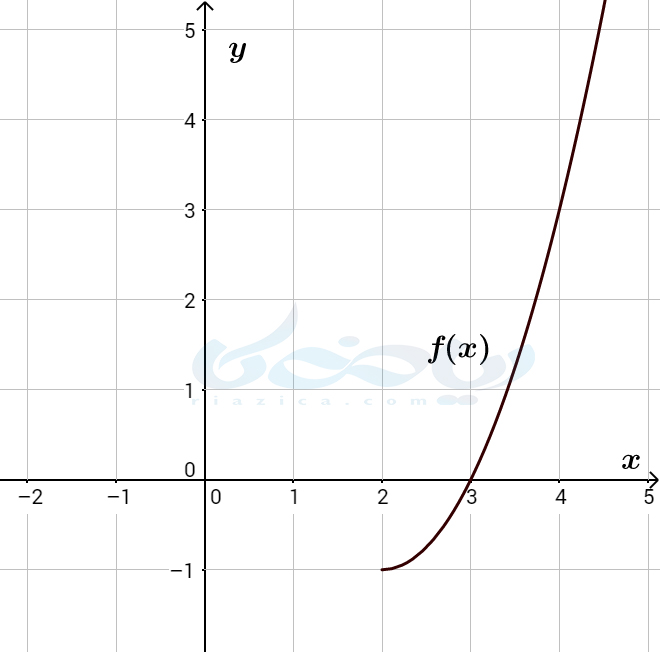
ضابطۀ تابع بعد از محدود کردن آن تغییری نکرده است. بنابراین کافی است تا \(\Large f(x) \) را بر حسب \(\Large f(y) \) با در نظر داشتن دامنۀ جدید به دست آوریم.
\(\LARGE y=x^2-4x+3 \)
\(\LARGE \Rightarrow y=(x-2)^2-1 \)
\(\LARGE \Rightarrow (x-2)^2=y+1 \)
\(\LARGE \Rightarrow x-2=\pm \sqrt{y+1} \)
\(\LARGE \Rightarrow x=\pm \sqrt{y+1}+2 \)
اما باید از علامت مثبت برای عبارت \(\Large \sqrt{y+1} \) استفاده کنیم یا منفی؟ نکتۀ بسیار جالب همین جاست. اگر دامنۀ تابع را محدود نمیکردیم، اکنون نمیتوانستیم بین علامت مثبت و منفی، یکی را بر دیگری ترجیح دهیم. اما چون دامنۀ تابع به بازۀ \(\Large [2,+\infty) \) محدود شده است، تنها علامت مثبت قابل قبول است. زیرا در غیر این صورت مقدار \(\Large x\) کوچکتر مساوی 2 خواهد شد. بنابراین داریم:
\(\LARGE x= \sqrt{y+1}+2 \)
\(\LARGE \Rightarrow f^{-1}(x)=\sqrt{x+1}+2 \)
اگر نمودار تابع با دامنۀ محدود شده و نمودار تابع وارون را رسم کنیم، شکل زیر به دست میآید. همان طور که میبینید، دو نمودار نسبت به خط \(\Large y=x\) قرینهاند.
توصیه میشه قبل از خوندن این پست ،پست وارون تابع ریاضی یازدهم مطالعه شود.
زنگ آخر کلاس تابع وارون
در درسنامهای که با یکدیگر خواندیم، ابتدا مروری کردیم بر مباحث مربوط به تابع وارون در پایۀ یازدهم. سپس بررسی کردیم در چه شرایطی دو تابع وارون یکدیگرند. همچنین به بررسی نحوۀ به دست آوردن ضابطۀ تابع وارون پرداختیم. در انتها نیز در مورد محدود کردن دامنۀ توابع غیر یک به یک و نحوۀ به دست آوردن وارون تابع محدود شده بحث کردیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث تابع وارون دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





اگر وارون یک تابع بسته باشد ایا میتوانونتیجه گرفت ان تابع پیوسته است
با سلام و عرض ادب
منظورتون از بسته بودن چی هست؟
سلام . میخواستم بپرسم وارون توابع چند ضابطه ای یا چه روشی ب دست میاد؟ ممنون
با سلام واحترام
اول باید ببینید تابع در کل دامنه یک به یک و وارون پذیر هست سپس هر وارون ضابطه را جدا گانه بدست آورید
سلام
وارون تابع |x|x_ چی میشه؟
با سلام وادب با شرط ایکس کوچکتر از صفر میشود رادیکال ایکس
سلام و عرض ادب . شاید ایکس کوچک تر از ۰ نبود .اونوقت چی
دوست عزیز در ازای ایکس های کوچکتر یا مساوی از صفر وارون پذیر است ولی بزرگتر از صفر اصلا وارون پذیر نیست
سلام
آیا میتونیم برای اینکه ثابت کنیم f و g وارون یکدیگرند، به جای ترکیبشون و رسیدن به تابع همانی، مستقیم وارون f رو محاسبه کنیم و به g برسیم؟
با سلام
بله میشه
سلام وارون تابع ایکس به توان ۳ ، فرجه ۳ ایکس هست ؟ آخه من جایی دیدم نوشته بود نیستند …
با سلام
درسته همین هست
وارون تابع درجه سه چطور بدست میاد ((X به توان 3)+X)
منم دنبال همینم
سلام دوست عزیز
باید جای x,y رو عوض کرد و بر اساس وای مرتب کرد البته همیشه کار راحتی نیست ودر اینجا توضیحش مشکله
سلام وقت بخیر
ببخشید من دنبال یه راه سریع هستم که تا هر ضابطه ای رو دیدم ،وارونش رو بنویسم، میشه راهنماییم کنید از کجا فرمول های سرعتی رو گیر بیارم
با سلام واحترام
راه سریعی نیست جای ایکس و وای رو عوض کنید وبعد وای رو تنها کنید
بله. تمام اعمالی که بر روی ایکس نجام شده رو بنویسید . بعد همرو برعکس بنویسید .
مثلا ایکس ضربدر 2 شده برای نوشتن وارون ایکس رو تقسیم بر 2 کنید و غیره…
سلام وارون این تابع چه جوری محاسبه میشه |y=3x+|x
به خاطر وجود قدر مطلق بازه بندی میکنیم
در ایکس بزرگتر از صفر میشه 4 ایکس که وارونش میشه ایکس چهارم
در ایکس های کوچکتر از صفر میشه دو ایکس که وارونش میشه ایکس دوم
سلام آیا شرطی وجود دارد که بدون نوشتن ضابطه وارون تابع ایکس بتوان تشخیص که ضابطه تابع و وارون آن یکی هستند؟
با سلام فقط تابع y=x ابعی هست که با وارونش برابر است
توابع خطی باشیب منفی یک و توابع هموگرافیک در شرایط خاص هم با وارونشون برابرن
سلام در چ صورتی تابع و وارونش برابرن
تابع همانی
سلام
وارون تابع X2_1به روی X در بازه ۳تا مثبت بی نهایت چیست
با سلام
وارون توابعی به فرم وای مساوی با ایکس به توان 3 بعلاوه 2ایکس را با چه روشی و چگونه می توان بدست
اورد؟
سلام دوست عزیز
در این توابع وقتی جای ایکس و وای رو عوض کردیم برای حل اون معادله درجه سه از روش نیوتن -رافسون یا نرم افزارهای محاسباتی استفاده کرد که در حوضه کار ما نیست