آموزش ریاضی پایه نهم
حجم هرم و مخروط ریاضی نهم 💎🔮 – محاسبه سریع و تند!
در درسنامهٔ حجم هرم و مخروط ریاضی نهم ابتدا هرم را معرفی میکنیم. سپس، اجزای هرم را بررسی کرده و با هرم منتظم آشنا میشویم. در ادامه، روش محاسبهٔ حجم هرم را بررسی کرده و با اثبات آن آشنا میشویم. در انتها نیر مخروط را معرفی کرده و حجم آن را به دست می آوریم. با ما تا انتهای درسنامهٔ حجم هرم و مخروط ریاضی نهم همراه باشید.
هرم چیست؟
تعریف هرم: به یک چندوجهی که قاعدهٔ آن چندضلعی و وجههای جانبی آن مثلث باشند، هرم میگوییم.
در شکل زیر میتوانید هرمهای مختلف با قاعدههای متفاوت را مشاهده کنید:

اجزای یک هرم با قاعدهٔ چهار ضلعی را در شکل زیر مشخص کردهایم:
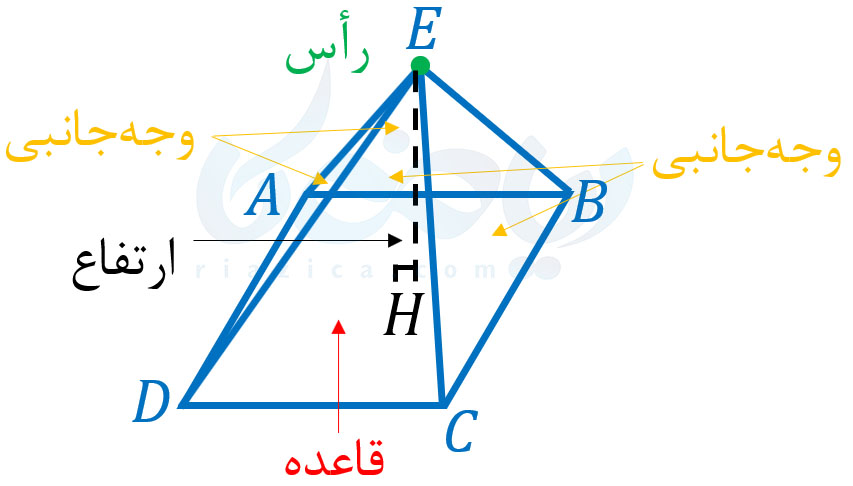
همان طور که در شکل بالا مشاهده میکنید، رأس هرم نقطهٔ \(\Large E\) است. وجههای جانبی آن، مثلثهای \(\Large EBC\) و \(\Large ECD\) و \(\Large EDA\) و \(\Large EAB\) هستند. همچنین، قاعدهٔ آن نیز، چهارضلعی \(\Large ABCD\) است. به عمودی که از رأس هرم بر قاعدهٔ آن رسم میکنیم، ارتفاع هرم میگوییم. در شکل بالا، ارتفاع هرم را با \(\Large EH\) نشان دادهایم. در صورتی که قاعدهٔ هرم، چندضلعی منتظم باشد، به آن هرم، هرم منتظم میگوییم. در هرمهای منتظم، ارتفاع هرم و قاعدهٔ آن، یکدیگر را در مرکز تقارن قاعدهٔ هرم قطع میکنند.
حجم هرم ریاضی نهم
حجم هرمی که مساحت قاعدهٔ آن برابر با \(\Large S\) و اندازهٔ ارتفاع آن برابر با \(\Large h\) است، از رابطهٔ زیر به دست میآید:

اثبات رابطهٔ حجم هرم
رابطهای که برای حجم هرم نشان داددیم را هم میتوان با استفاده از انتگرال و هم با استفاده از قضیهٔ کاوالیری ثابت کرد. در اینجا از روش دوم استفاده میکنیم. با استفاده از قضیهٔ کاوالیری میتوان ثابت کرد در صورتی که مساحت قاعدهٔ دو هرم و اندازهٔ ارتفاع آنها با یکدیگر برابر باشد، حجم دو هرم با یکدیگر برابر است (در صورتی که علاقهمندید در مورد انتگرال و قضیهٔ کاوالیری مطالعه کنید). حال منشور زیر را در نظر بگیرید:
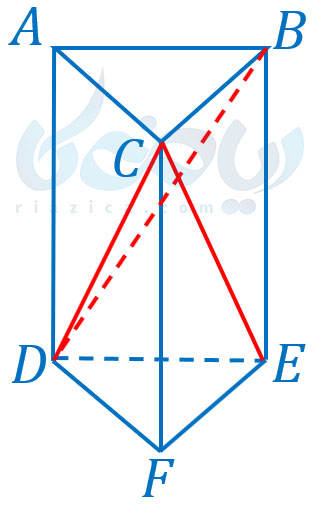
میخواهیم از روی خطوط قرمز رنگ بالا، منشور را به سه هرم تقسیم کنیم. برای اینکه بهتر متوجه شوید، به شکل زیر دقت کنید:
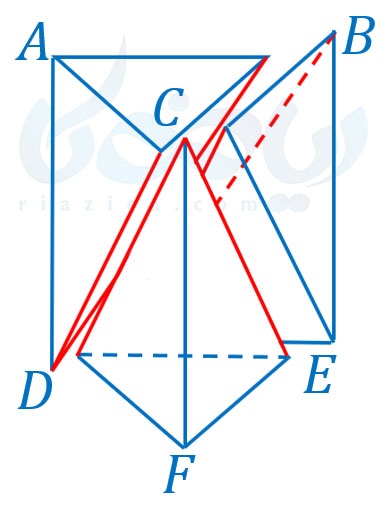
در قسمت بعد ثابت میکنیم حجم این سه هرم با یکدیگر برابر است. در نتیجه، چون حجم منشور را میدانیم، حجم هر هرم برابر با \(\Large \frac{1}{3}\) حجم منشور خواهد شد.
اثبات برابری حجم سه هرم
از آنجاییکه هرمهای ما دارای وجوه سه ضلعی هستند، می توان یکی از وجوه را به دلخواه قاعده گرفت و وجوه دیگر را به عنوان وجههای جانبی به حساب آورد. به این ترتیب میتوانیم قاعدهٔ هرم \(\Large ABCD\) را، مثلث \(\Large ABC\) در نظر بگیریم. همچنین قاعدهٔ هرم \(\Large CDEF\) را مثلث \(\Large DEF\) در نظر بگیریم. پس، دو هرم \(\Large ABCD\) و \(\Large CDEF\) دارای قاعدهها و ارتفاعهای برابر هستند. بنابراین، حجم دو هرم \(\Large ABCD\) و \(\Large CDEF\) با هم برابر است. از طرفی، دو هرم \(\Large ABCD\) و \(\Large EBCD\) نیز دارای حجمهای برابرند. زیرا میتوان قاعدهٔ هرم \(\Large ABCD\) را مثلث \(\Large ABD\) در نظر گرفت. قاعدهٔ هرم \(\Large EBCD\) را نیز میتوان مثلث \(\Large BDE\) در نظر گرفت. در این صورت، مساحت قاعدهٔ هر کدام از این دو هرم برابر است با نصف مساحت مستطیل \(\Large ABED\). ارتفاع آنها نیز با هم برابر است. در نتیجه، دو هرم \(\Large ABCD\) و \(\Large EBCD\) دارای حجمهای برابر هستند.
پس حجم هرم\(\Large ABCD\)، هم برابر با حجم هرم \(\Large CDEF\) است و هم برابر با حجم هرم \(\Large EBCD\). پس حجم سه هرم با یکدیگر برابر است.
استخراج رابطهٔ حجم هرم
بنابراین حجم هر هرم برابر است با یک سوم حجم منشور. همان طور که در درسنامهٔ محاسبه حجم های منشوری هفتم خواندیم، حجم منشور برابر است با حاصل ضرب مساحت قاعده در ارتفاع. بنابراین حجم هر هرم بالا برابر است با \(\Large \frac{1}{3}\) حجم منشور بالا، یعنی برابر است با \(\Large \frac{1}{3}\) مساحت قاعده ضرب در ارتفاع. بنابراین، برای حجم هرم، رابطهٔ زیر برقرار است:
\(\LARGE V=\frac{1}{3}Sh\)
اگر قاعدهٔ منشور، شکل دیگری به غیر از مثلث بود هم همین اتفاق میافتاد؛ یعنی میتوانستیم آن را به سه هرم با حجم مساوی تقسیم کنیم. در تصویر متحرک زیر میتوانید چگونگی تقسیم یک منشور با قاعدهٔ مربع را به سه هرم با حجم مساوی مشاهده کنید:

مثال از حجم هرم ریاضی نهم
مثال 1: حجم هرم زیر را به دست آورید.
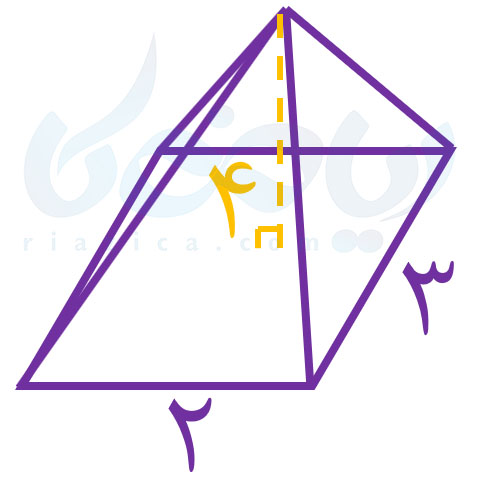
حل: همان طور که در شکل بالا میبینید، قاعدهٔ هرم، یک مستطیل با اضلاع \(\Large 2\) و \(\Large 3\) است. بنابراین مساحت قاعده برابر است با \(\Large 6\). ارتفاع هرم نیز برابر با \(\Large 4\) است. بنابراین داریم:
\(\LARGE V=\frac{1}{3}Sh\)
\(\LARGE \Rightarrow V=\frac{1}{3} \times 6 \times 4=8\)
مثال از حجم هرم ریاضی نهم
مثال 2: هرمی با ارتفاع \(\Large 10\) و قاعدهٔ مثلث داریم. اندازهٔ اضلاع قاعده برابر با \(\Large 6\) و \(\Large 8\) و \(\Large 10\) هستند. حجم هرم را به دست آورید.
حل: اگر دقت کنید، اندازهٔ اضلاع قاعده، در رابطهٔ فیثاغورس صدق میکنند. یعنی داریم:
\(\LARGE 6^2+8^2=10^2\)
بنابراین همان طور که در درسنامهٔ رابطهٔ فیثاغورس ریاضی هشتم خواندیم، طبق عکس رابطهٔ فیثاغورس میتوان نتیجه گرفت که قاعدهٔ هرم، مثلث قائمالزاویه با قاعدههایی با ابعاد \(\Large 6\) و \(\Large 8\) است. بنابراین مساحت قاعدهٔ هرم برابر است با:
\(\LARGE S=\frac{6 \times 8}{2}=24\)
حال که هم مساحت قاعدهٔ هرم را میدانیم و هم اندازهٔ ارتفاع آن را، میتوانیم حجم هرم را به دست آوریم:
\(\LARGE V=\frac{1}{3}Sh\)
\(\LARGE =\frac{1}{3} \times 24 \times 10\)
\(\LARGE =80\)
مثال از حجم هرم ریاضی نهم
مثال 3: حجم شکل زیر را بیابید.
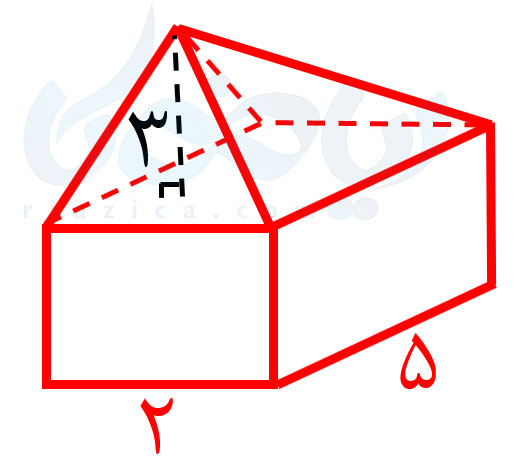
حل: حجم شکل بالا برابر است با مجموع حجم یک مکعب مستطیل و حجم یک هرم. حجم هرم برابر است با \(\Large \frac{1}{3}\) حاصل ضرب مساحت قاعده ضرب در ارتفاع. بنابراین، اگر حجم هرم را با \(\Large V_p\) نشان دهیم، داریم:
\(\LARGE V_p=\frac{1}{3}Sh\)
\(\LARGE \Rightarrow V_p=\frac{1}{3}\times (2 \times 5) \times 3\)
\(\LARGE \Rightarrow V_p=10\)
همچنین، اگر حجم مکعب مستطیل را با \(\Large V_c\) نشان دهیم، داریم:
\(\LARGE V_c=2 \times 5 \times 3=30\)
بنابراین حجم شکل که از مجموع حجم هرم و مکعب مستطیل به دست می آید، برابر است با:
\(\LARGE V=V_p+V_c\)
\(\LARGE \Rightarrow V=10+30=40\)
مخروط چیست؟
در صورتی که قاعدهٔ یک هرم به جای چندضلعی، دایره باشد، مخروط به وجود میآید. بدیهی است در این حالت، وجوه مثلی نیز نداریم. در شکل زیر یک مخروط با شعاع قاعدهٔ \(\Large R\) و ارتفاع \(\Large h\) را مشاهده کنید.
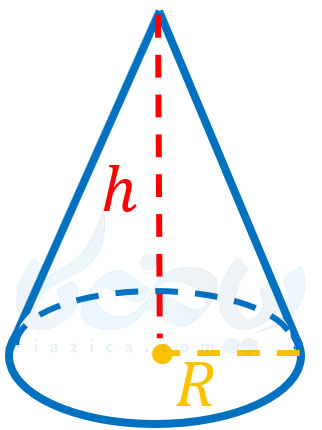
میتوان گفت مخروط، حالت حدی یک هرم منتظم است؛ یعنی هرمی که قاعدهٔ آن یک بینهایت ضلعی منتظم است. البته همان طور که در درسنامهٔ حجم و سطح ریاضی هفتم خواندید، میتوان با استفاده از دوران مثلث نیز، مخروط به دست آورد.
حجم مخروط ریاضی نهم
مشابه با هرم، حجم مخروط را نیز، هم میتوان با استفاده از انتگرال و هم با استفاده از قضیهٔ کاوالیری به دست آورد. به این ترتیب، حجم مخروط برابر است با \(\Large \frac{1}{3}\) حاصل ضرب مساحت قاعده در ارتفاع. از آنجاییکه قاعدهٔ مخروط، دایره است، مساحت قاعده از رابطهٔ \(\Large S=\pi R^2\) به دست میآید. بنابراین داریم:

مثال از حجم مخروط ریاضی نهم
مثال 4: حجم مخروط زیر را بیابید (مقدار \(\Large \pi\) را برابر با \(\Large 3\) در نظر بگیرید).
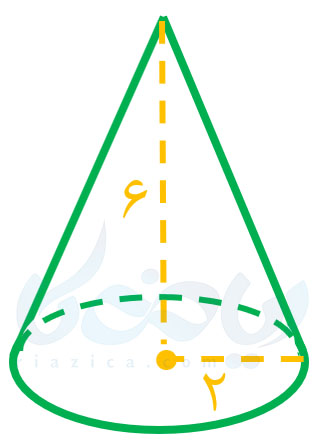
حل: همان طور که دیدیم، حجم مخروط از رابطهٔ \(\Large V=\frac{1}{3} \pi R^2 h\) به دست میآید. اندازهٔ شعاع قاعدهٔ مخروط برابر با \(\Large 2\) و اندازهٔ ارتفاع آن برابر با \(\Large 6\) است. بنابراین حجم مخروط برابر است با:
\(\LARGE V=\frac{1}{3} \pi R^2 h\)
\(\LARGE \Rightarrow V=\frac{1}{3} \times 3 \times 2^2 \times 6\)
\(\LARGE \Rightarrow V=24\)
مثال از حجم مخروط ریاضی نهم
مثال 5: یک ساعت شنی داریم که در مخروط بالایی آن، شن به حجم \(\Large 20\) وجود دارد. مساحت قاعدهٔ مخروط، برابر با \(\Large 6\) است. بعد از اینکه کل شن به مخروط پایینی منتقل شود، تا چه ارتفاعی بالا میآید؟
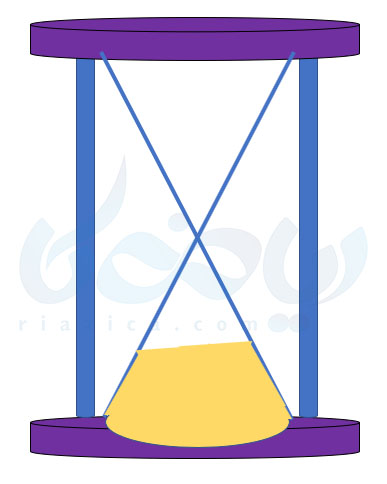
حل: حجم شنی که در مخروط پایینی ریخته میشود، برابر است با \(\Large \frac{1}{3}Sh\) که در این رابطه، \(\Large S\) برابر است با مساحت قاعدهٔ مخروط و \(\Large h\) برابر است با اندازهٔ ارتفاع آن. از طرفی حجم این مقدار شن برابر است با \(\Large 20\). بنابراین داریم:
\(\LARGE 20=\frac{1}{3}Sh\)
\(\LARGE \Rightarrow 20=\frac{1}{3} \times 6 \times h\)
\(\LARGE \Rightarrow 20=2 \times h\)
\(\LARGE \Rightarrow h=10\)
مثال از حجم مخروط ریاضی نهم
مثال 6: حجم شکل زیر را بیابید (مقدار \(\Large \pi\) را برابر با \(\Large 3\) در نظر بگیرید).
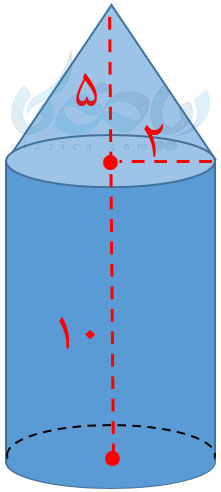
حل: حجم شکل بالا برابر است با مجموع حجم یک استوانه و یک مخروط. همان طور که در درسنامهٔ محاسبه ی حجم های منشوری هفتم خواندیم، حجم استوانه برابر است با مساحت قاعدهٔ آن ضرب در ارتفاع. بنابراین اگر حجم استوانه را با \(\Large V_r\) و حجم مخروط را با \(\Large V_e\) نشان دهیم، داریم:
\(\LARGE V_r=\pi R^2h\)
\(\LARGE \Rightarrow V_r=3 \times 2^2 \times 10=120\)
\(\LARGE V_e=\frac{1}{3}\pi R^2h\)
\(\LARGE \Rightarrow V_e=\frac{1}{3} \times 3 \times 2^2 \times 5\)
\(\LARGE \Rightarrow V_e=20\)
بنابراین حجم شکل که از مجموع حجم استوانه و مخروط به دست میآید، برابر است با:
\(\LARGE V=V_r+V_e\)
\(\LARGE \Rightarrow V=120+20=140\)
زنگ آخر کلاس حجم هرم و مخروط ریاضی نهم
در درسنامهای که از ریاضی نهم خواندیم، ابتدا هرم را معرفی کرده و نحوهٔ به دست آوردن حجم آن را بررسی کردیم. در ادامه، مخروط را به عنوان یک حالت حدی از هرم منتظم دیدیم و حجم آن را به دست آوردیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با حجم هرم و مخروط ریاضی نهم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





خوب بود :)?
خدا روشکر که پسندیدید
عالی بود
خیلی ممنون
با سلام و سپاس از توضیحات جامع و عالی تون