آموزش ریاضی پایه نهم
تقسیم چند جمله ای ها نهم ➗🔤 – ۳ نوع تقسیم مهم!
در درسنامهٔ تقسیم چند جمله ای ها نهم سه مورد زیر را بررسی میکنیم:
- تقسیم یک جملهای بر یک جملهای
- تقسیم چند جملهای بر یک جملهای
- تقسیم چند جملهای بر چند جملهای
قبل از شروع درسنامه باید گفت که هر کسری نشان دهندهٔ یک تقسیم است. بنابراین سادهسازی کسرهای یک جملهای و چند جملهای در واقع همان محاسبهٔ تقیسم آنها بر هم است. سعی میکنیم با حل مثال از هر قسمت، به درک بهتر شما از مبحث کمک کنیم. به اولین قسمت از درسنامهٔ تقسیم چند جمله ای ها نهم توجه کنید.
تقسیم یک جملهای بر یک جملهای
برای تقسیم یک جملهای بر یک جملهای باید اعداد را با هم و متغیرهای یکسان را با یکدیگر ساده کنیم. اگر توان یک متغیر در صورت کسر، بیشتر از توان همان متغیر در مخرج کسر بود، توان مخرج را از صورت کم کرده و در صورت قرار میدهیم. برعکس، اگر توان یک متغیر در مخرج کسر بیشتر از توان همان متغیر در صورت کسر بود، توان صورت را از مخرج کم کرده و در مخرج قرار میدهیم. برای اینکه بهتر متوجه شوید، به مثال بعدی توجه کنید.
مثال از درسنامهٔ تقسیم چند جمله ای ها نهم
مثال 1: تقسیم \(\Large \frac{4xy^5}{-8x^3y^2z}\) را انجام دهید.
حل: عدد \(\Large 4\) در صورت را با عدد \(\Large -8\) در مخرج ساده میکنیم؛ بنابراین، عدد \(\Large -2\) در مخرج باقی میماند. توان متغیر \(\Large x\) در صورت برابر با \(\Large 1\) و توان آن در مخرج برابر با \(\Large 3\) است. بنابراین، \(\Large 3-1\) را که برابر با \(\Large 2\) است، به عنوان توان \(\Large x\) در مخرج قرار میدهیم. توان متغیر \(\Large y\) در صورت برابر با \(\Large 5\) و توان آن در مخرج برابر با \(\Large 2\) است. بنابراین، \(\Large 5-2\) را که برابر با \(\Large 3\) است، به عنوان توان \(\Large y\) در صورت قرار میدهیم. آنچه که گفتیم را میتوانید در شکل زیر مشاهده کنید:
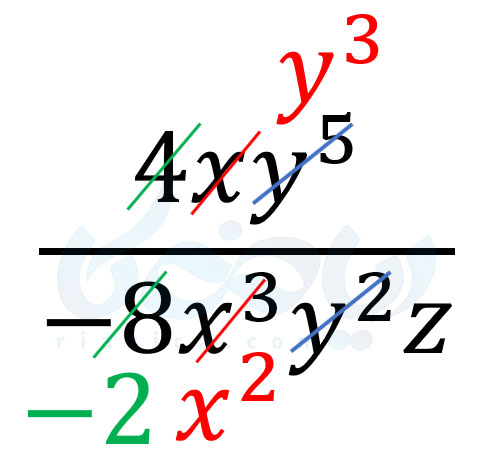
به قسمت بعدی از درسنامهٔ تقسیم چند جمله ای ها نهم توجه کنید.
تقسیم چند جملهای بر یک جملهای
برای تقسیم چند جملهای بر یک جملهای میتوانیم به دو صورت عمل کنیم:
- متغیرهای مشترک بین جملات صورت را با کمترین توان فاکتور گرفته و با مخرج ساده کنیم.
- تقسیم چند جملهای بر یک جملهای را به صورت مجموع تقسیمهای یک جملهای بر یک جملهای نوشته و مجموع را به دست آوریم.
برای اینکه چگونگی استفاده از هر روش را مشاهده کرده و بر آنها مسلط شوید، دو مثال بعدی را با استفاده از هر دو روش حل میکنیم.
مثال از درسنامهٔ تقسیم چند جمله ای ها نهم
مثال 2: تقسیم \(\Large \frac{ab^2-a^2b^3c+b^2c}{a^2bc^2}\) را انجام دهید.
حل: همان طور که گفتیم، با استفاده از هر دو روش، مسئله را حل میکنیم.
روش اول: در صورت کسر، متغیر \(\Large b\) بین هر سه جملهٔ \(\Large ab^2\) و \(\Large -a^2b^3c\) و \(\Large b^2c\) مشترک است. کوچکترین توان متغیر \(\Large b\) بین این سه جمله برابر با \(\Large 2\) است. بنابراین \(\Large b^2\) را از صورت کسر فاکتور میگیریم. به این ترتیب داریم:
\(\LARGE \frac{b^2(a-a^2bc+c)}{a^2bc^2}\)
حال می توانیم \(\Large b^2\) در صورت کسر را با \(\Large b\) در مخرج ساده کنیم. در این صورت \(\Large b\) در صورت کسر باقی میماند:
\(\LARGE \frac{b^2(a-a^2bc+c)}{a^2bc^2}\)
\(\LARGE =\frac{b(a-a^2bc+c)}{a^2c^2}\)
روش دوم: کسر \(\Large \frac{ab^2-a^2b^3c+b^2c}{a^2bc^2}\) را میتوانیم به صورت مجموع چند کسر بنویسیم:
\(\LARGE \frac{ab^2-a^2b^3c+b^2c}{a^2bc^2}\)
\(\LARGE =\frac{ab^2}{a^2bc^2}-\frac{a^2b^3c}{a^2bc^2}+\frac{b^2c}{a^2bc^2}\)
هر کسر در عبارت بالا، تقسیم یک جملهای بر یک جملهای است. بنابراین میتوانیم هر کسر را با استفاده از مطالبی که در ابتدای درسنامه خواندیم، به صورت زیر ساده کنیم:
\(\LARGE \frac{ab^2}{a^2bc^2}-\frac{a^2b^3c}{a^2bc^2}+\frac{b^2c}{a^2bc^2}\)
\(\LARGE =\frac{b}{ac^2}-\frac{b^2}{c}+\frac{b}{a^2c}\)
مثال از درسنامهٔ تقسیم چند جمله ای ها نهم
مثال 3: تقسیم \(\Large \frac{x^2yz^5-3y^2z^4+2xyz^2}{x^2z^3}\) را انجام دهید.
حل: مانند مثال قبل، با استفاده از هر دو روش، مسئله را حل میکنیم.
روش اول: در صورت کسر، متغیرهای \(\Large y\) و \(\Large z\) بین هر سه جملهٔ \(\Large x^2yz^5\) و \(\Large -3y^2z^4\) و \(\Large 2xyz^2\) مشترک هستند. کمترین توان متغیر \(\Large y\) بین هر سه عبارت برابر با \(\Large 1\) و کمترین توان \(\Large z\) بین سه عبارت برابر با \(\Large 2\) است. بنابراین، عبارت \(\Large yz^2\) را از صورت کسر فاکتور میگیریم:
\(\LARGE \frac{x^2yz^5-3y^2z^4+2xyz^2}{x^2z^3}\)
\(\LARGE =\frac{yz^2(x^2z^3-3yz^2+2x)}{x^2z^3}\)
حال \(\Large z^2\) را در صورت، با عبارت \(\Large z^3\) در مخرج ساده میکنیم:
\(\LARGE \frac{yz^2(x^2z^3-3yz^2+2x)}{x^2z^3}\)
\(\LARGE =\frac{y(x^2z^3-3yz^2+2x)}{x^2z}\)
روش دوم: کسر را به صورت مجموع چند کسر مینویسیم:
\(\LARGE \frac{x^2yz^5-3y^2z^4+2xyz^2}{x^2z^3}\)
\(\LARGE =\frac{x^2yz^5}{x^2z^3}-\frac{3y^2z^4}{x^2z^3}+\frac{2xyz^2}{x^2z^3}\)
حال هر کسر را که تقسیم یک جملهای بر یک جملهای است، ساده میکنیم:
\(\LARGE \frac{x^2yz^5}{x^2z^3}-\frac{3y^2z^4}{x^2z^3}+\frac{2xyz^2}{x^2z^3}\)
\(\LARGE =\frac{yz^2}{1}-\frac{3y^2z}{x^2}+\frac{2y}{xz}\)
\(\LARGE =yz^2-\frac{3y^2z}{x^2}+\frac{2y}{xz}\)
به قسمت بعدی از درسنامهٔ تقسیم چند جمله ای ها نهم توجه کنید.
تقسیم چند جملهای بر چند جملهای
ابتدا باید گفت که در دبیرستان به دبنال تقسیم چندجملهای بر چندجملهای با حداکثر یک متغیر هستیم. در واقع در هر دو عبارت، حداکثر یک متغیر وجود دارد و متغیر دو عبارت یکسان است. حال به سراغ توضیح چگونگی تقسیم چنین عباراتی میرویم. همان طور که به خاطر دارید، دو عدد طبیعی را میتوانیم به صورت زیر بر یکدیگر تقسیم کنیم:
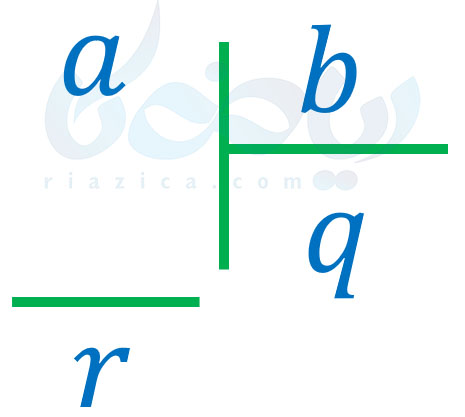
در تقسیم بالا، به \(\Large a\) مقسوم، به \(\Large b\) مقسومُعلیه، به \(\Large q\) خارج قسمت و به \(\Large r\) باقیمانده میگفتیم. همچنین، در هر تقسیمی همیشه باقیمانده کوچکتر از مقسومُعلیه بود. یعنی به طور مثال در تقسیم بالا، \(\Large r<b\) است. برای تقسیم دو چندجملهای بر هم، ابتدا مقسوم و مقسومُعلیه را بر حسب توانهای متغیر، از بزرگ به کوچک مرتب میکنیم. سپس، اولین جمله از مقسوم را بر اولین جمله از مقسومُعلیه تقسیم کرده و این روند را ادامه میدهیم. در واقع فرآیند تقسیم، مشابه با آن چیزی است که در تقسیم اعداد طبیعی دیدید. صرفاً خواندن این توضیح، به درک شما کمک نمیکند؛ به همین منظور، چگونگی تقسیم چند جملهایها را با حل مثال آموزش میدهیم. به مثال بعدی از درسنامهٔ تقسیم چند جمله ای ها نهم توجه کنید.
یادگیری تقسیم چندجملهایها با حل مثال
مثال 4: چندجملهای \(\Large 10x+3x^2+8\) را بر چندجملهای \(\Large x+2\) تقسیم کرده و خارج قسمت و باقیمانده را به دست آورید.
حل: همان طور که گفتیم، ابتدا باید مقسوم و مقسومُعلیه را بر حسب توان متغیر از بزرگ به کوچک مرتب کنیم. مرتب شدهٔ مقسوم، به صورت \(\Large 3x^2+10x+8\) خواهد بود. مقسومُعلیه هم که همان \(\Large x+2\) است، از قبل مرتب شده است. بنابراین باید حاصل تقسیم زیر را حساب کنیم:
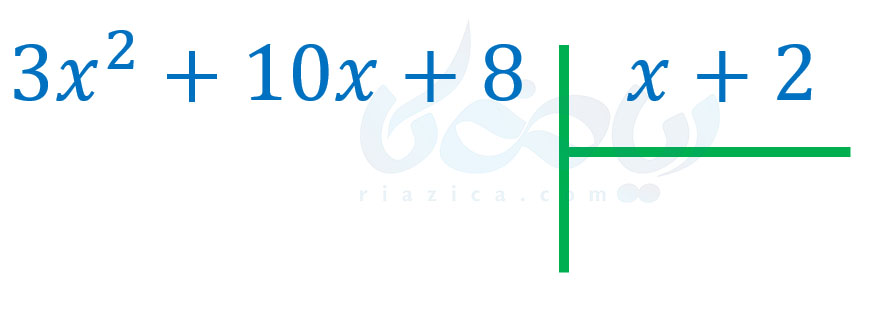
همان طور که گفتیم، باید اولین جملهٔ مقسوم را بر اولین جملهٔ مقسومُعلیه تقسیم کنیم. یعنی باید حاصل \(\Large \frac{3x^2}{x}\) را به دست آوریم. همان طور که میبینید، عبارت \(\Large \frac{3x^2}{x}\) تقسیم یک جملهای بر یک جملهای است و حاصل آن برابر با \(\Large 3x\) است. بنابراین داریم:

حال باید حاصل ضرب \(\Large 3x\) در \(\Large x+2\) را به دست آوریم. درست مانند کاری که در تقسیم اعداد طبیعی انجام میدادیم. بنابراین داریم:
\(\LARGE 3x(x+2)=3x^2+6x\)
پس تقسیم ما تا اینجا به صورت زیر در میآید:
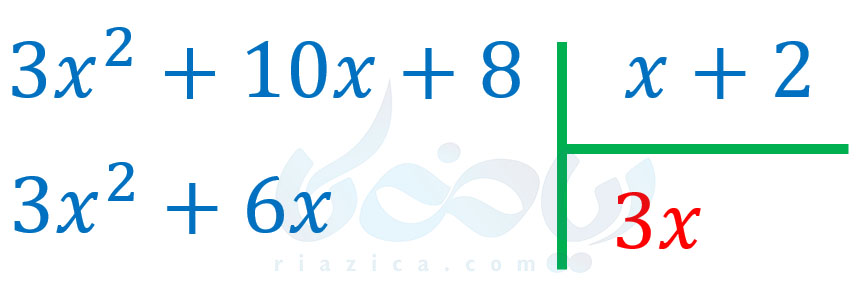
در این مرحله باید \(\Large 3x^2+6x\) را از \(\Large 3x^2+10x+8\) کم کنیم:
\(\LARGE 3x^2+10x+8-(3x^2+6x)\)
\(\LARGE =3x^2+10x+8-3x^2-6x\)
\(\LARGE =4x+8\)
بنابراین، تقسیم به شکل زیر در میآید:
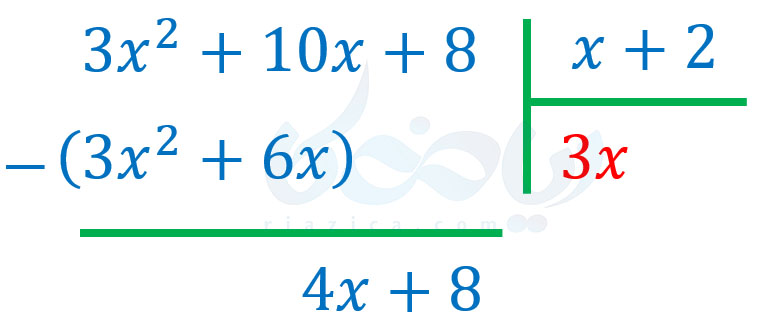
حال باید اولین جملهٔ عبارت \(\Large 4x+8\) را که \(\Large 4x\) است، بر اولین جملهٔ عبارت \(\Large x+2\) که \(\Large x\) است، تقسیم کنیم. حاصل \(\Large \frac{4x}{x}\) برابر با \(\Large 4\) است. پس داریم:
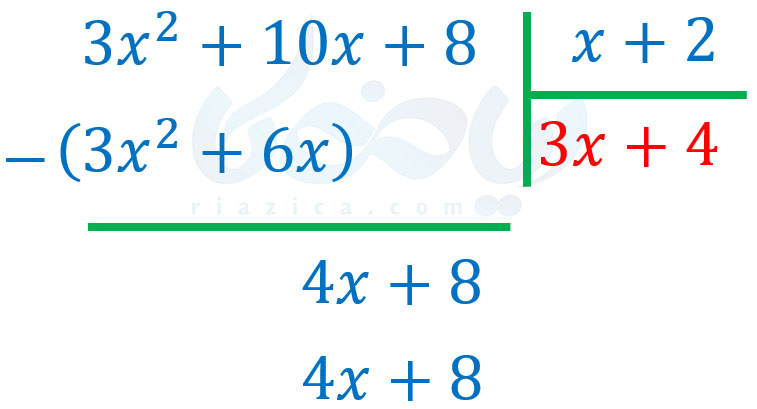
بنابراین، این بار \(\Large 4\) رادر \(\Large x+2\) ضرب کرده و از عبارت \(\Large 4x+8\) کم میکنیم. حاصل ضرب \(\Large 4\) در \(\Large x+2\) برابر با \(\Large 4x+8\) است. پس داریم:
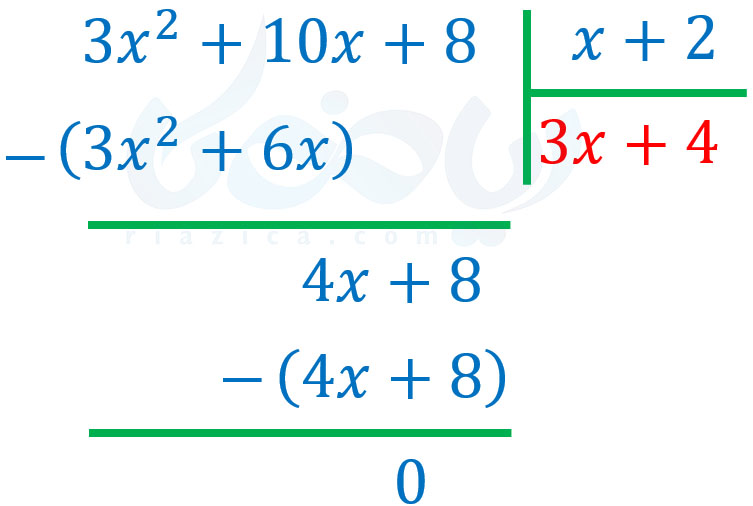
همان طور که دیدید، خارج قسمت برابر با \(\Large 3x+4\) و باقیمانده برابر با صفر شد. مانند اعداد طبیعی، در این حالت میگوییم مقسوم بر مقسومُعلیه بخش پذیر است. شرط باقیمانده در تقسیم نیز برقرار است. یعنی در اینجا، باقیمانده که همان \(\Large 0\) است، از مقسومُعلیه که \(\Large x+2\) است کوچکتر است. منظور از کوچکتر بودن، کوچکتر بودن درجهٔ عبارت \(\Large 0\) از درجهٔ چندجملهای \(\Large x+2\) است.
مثال از درسنامهٔ تقسیم چند جمله ای ها نهم
مثال 5: چندجملهای \(\Large 3x^4-2x^2-2x-7\) را بر چندجملهای \(\Large -2+x^2\) تقسیم کرده و رابطههای تقسیم را بنویسید.
حل: ابتدا مقسوم و مقسومُعلیه را بر حسب توان \(\Large x\) از بزرگ به کوچک مرتب میکنیم:
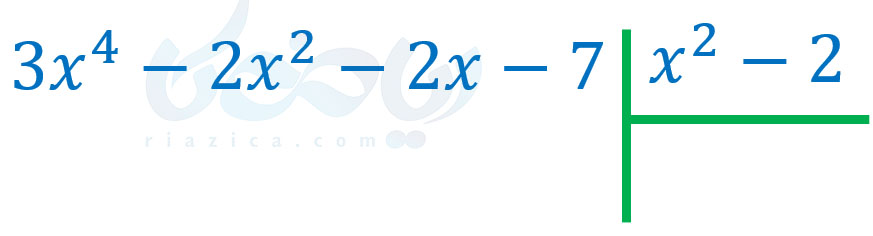
حال کافی است جملهٔ اول مقسوم را که \(\Large 3x^4\) است، بر جملهٔ اول مقسومُعلیه که \(\Large x^2\) است تقسیم کنیم. حاصل \(\Large \frac{3x^4}{x^2}\) برابر با \(\Large 3x^2\) است. بنابراین عبارت \(\Large 3x^2\) را در خارج قسمت نوشته و حاصل ضرب \(\Large 3x^2\) در \(\Large x^2-2\) را زیر مقسوم مینویسیم:
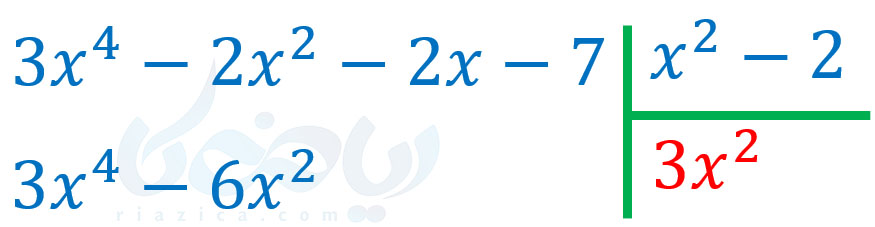
در مرحلهٔ بعدی باید \(\Large 3x^4-6x^2\) را از \(\Large 3x^4-2x^2-2x-7\) کم کنیم. برای خلاصه نویسی، عبارت \(\Large 3x^4-6x^2\) را که زیر مقسوم است، قرینه کرده و با مقسوم به صورت زیر جمع میکنیم:
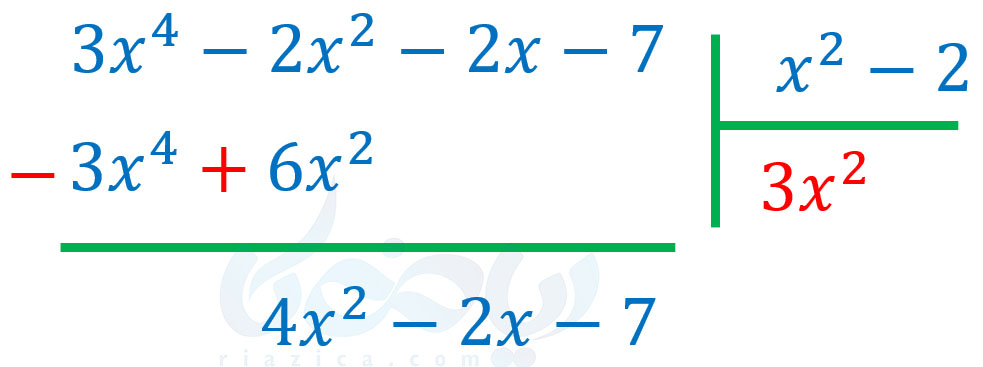
حال باید جملهٔ اول عبارت \(\Large 4x^2-2x-7\) را که \(\Large 4x^2\) است، بر جملهٔ اول \(\Large x^2-2\) که \(\Large x^2\) است تقسیم کنیم. حاصل \(\Large \frac{4x^2}{x^2}\) برابر با \(\Large 4\) است. بنابراین \(\Large 4\) را در خارج قسمت نوشته و در مقسومُعلیه که \(\Large x^2-2\) است ضرب کرده و زیر عبارت \(\Large 4x^2-2x-7\) مینویسیم:
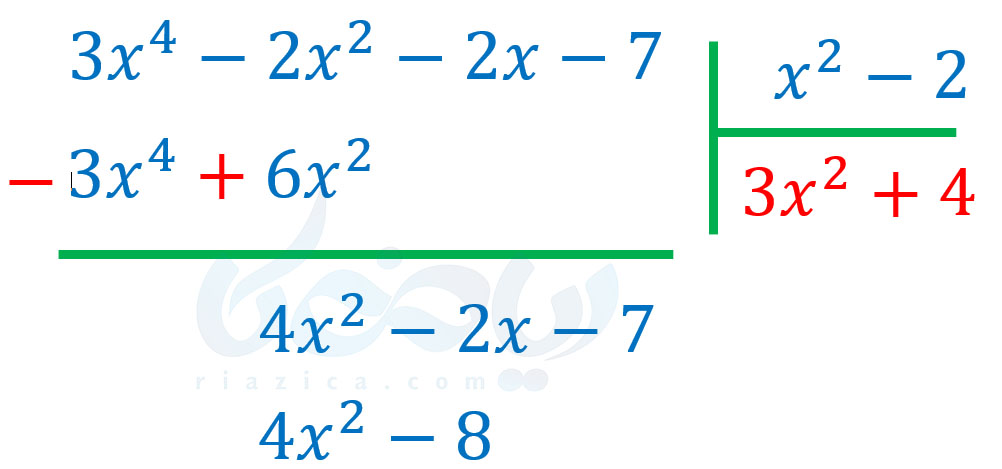
مانند مرحلهٔ قبل، \(\Large 4x^2-8\) را قرینه کرده و با \(\Large 4x^2-2x-7\) جمع می کنیم. حاصل برابر با \(\Large -2x+1\) میشود:
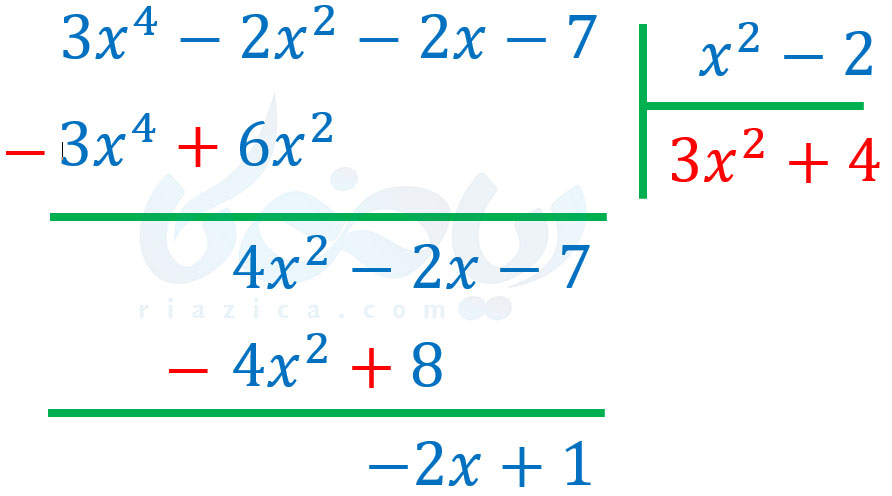
همان طور که میبینید، درجهٔ چندجملهای \(\Large -2x+1\) برابر با یک و درجهٔ مقسومُعلیه که \(\Large x^2-2\) است، برابر با \(\Large 2\) است. پس، درجهٔ باقیمانده کوچکتر از درجهٔ مقسومُعلیه شد و دیگر نمیتوانیم تقسیم را ادامه دهیم. از آنجاییکه صورت مثال، از ما رابطههای تقسیم را خواسته، باید بنویسیم:
\(\LARGE 3x^4-2x^2-2x-7\)
\(\Large =(x^2-2)(3x^2+4)-2x+1\)
همچنین باید ذکر کنیم که درجهٔ چندجملهای \(\Large -2x+1\) کمتر از درجهٔ \(\Large x^2-2\) است.
مثال از درسنامهٔ تقسیم چند جمله ای ها نهم
مثال 6: چندجملهای \(\Large y^5+2y^4+y^3+y^2+y\) را بر چندجملهای \(\Large y^3+y^2\) تقسیم کرده و رابطههای تقسیم را بنویسید.
حل: هم مقسوم و هم مقسومُعلیه مرتب است. جملهٔ اول مقسوم را که \(\Large y^5\) است، بر جملهٔ اول مقسومُعلیه که \(\Large y^3\) است تقسیم میکنیم. حاصل \(\Large \frac{y^5}{y^3}\) برابر با \(\Large y^2\) میشود. بنابراین، \(\Large y^2\) را در خارج قسمت نوشته و حاصل ضرب \(\Large y^2\) در \(\Large y^3+y^2\) را زیر مقسوم مینویسیم:
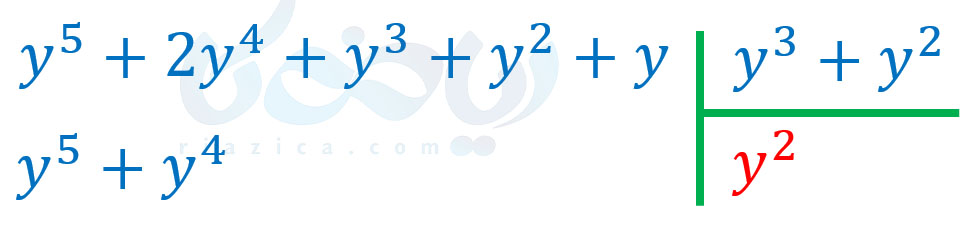
عبارت \(\Large y^5+y^4\) را قرینه کرده و با \(\Large y^5+2y^4+y^3+y^2+y\) جمع میکنیم:
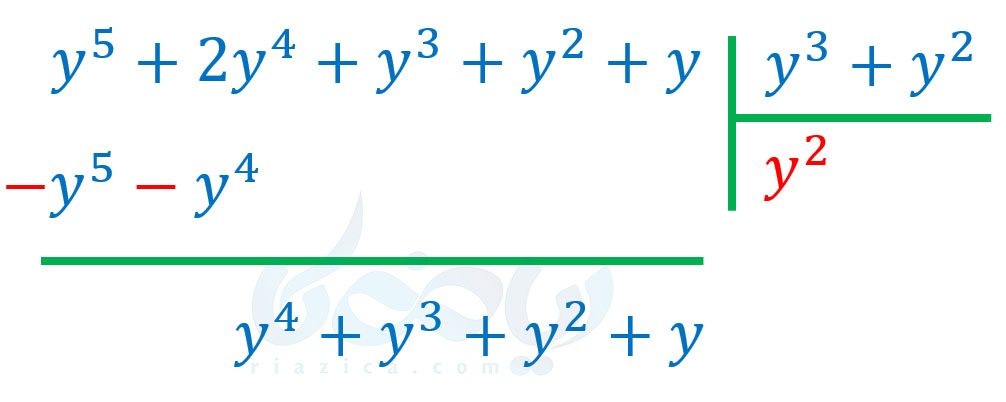
حال باید جملهٔ اول عبارت \(\Large y^4+y^3+y^2+y\) را که \(\Large y^4\) است، بر جملهٔ اول \(\Large y^3+y^2\) که \(\Large y^3\) است تقسیم کنیم. حاصل \(\Large \frac{y^4}{y^3}\) برابر با \(\Large y\) میشود. بنابراین، \(\Large y\) را در \(\Large y^3+y^2\) ضرب میکنیم:
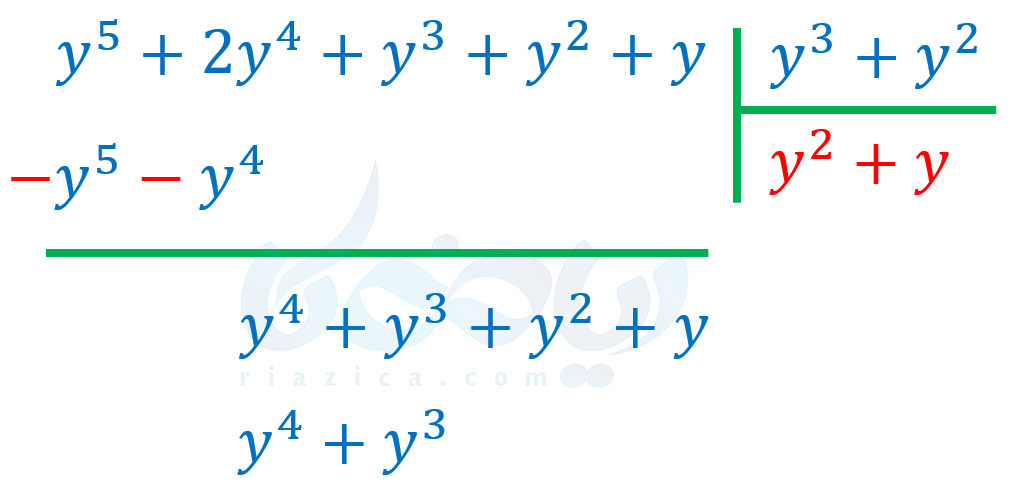
عبارت \(\Large y^4+y^3\) را قرینه کرده و با \(\Large y^4+y^3+y^2+y\) جمع میکنیم:
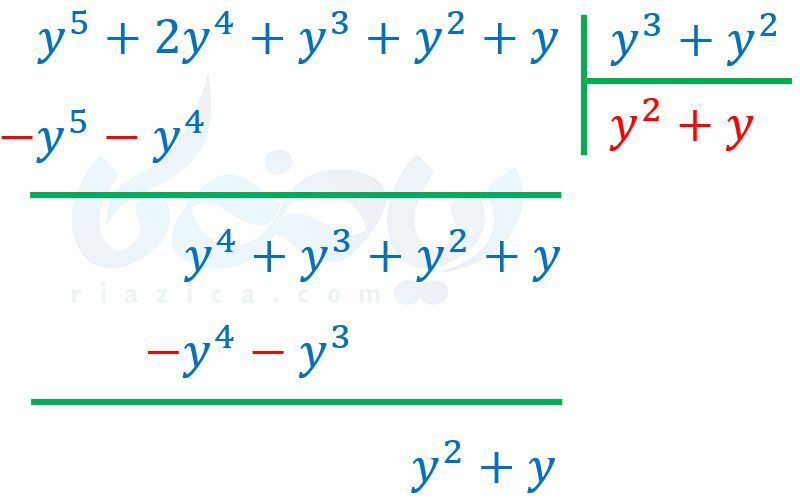
باقیمانده برابر با \(\Large y^2+y\) شد که چندجملهای درجه دوم است. مقسومُعلیه، چندجملهای درجه سوم است. بنابراین دیگر نمیتوانیم تقسیم را ادامه دهیم. پس رابطهٔ تقسیم به صورت زیر است:
\(\LARGE y^5+2y^4+y^3+y^2+y \)
\(\Large =(y^3+y^2)(y^2+y)+y^2+y\)
همچنین، باید ذکر کنیم که درجهٔ \(\Large y^2+y\) کوچکتر از درجهٔ \(\Large y^3+y^2\) است.
زنگ آخر کلاس تقسیم چند جمله ای ها نهم
در درسنامهای که از ریاضی نهم خواندیم، سه مورد زیر را بررسی کردیم:
- تقسیم یک جملهای بر یک جملهای
- تقسیم چند جملهای بر یک جملهای
- تقسیم چند جملهای بر چند جملهای
همان طور که دیدید، دانستن چگونگی تقسیم یک جملهایها به ما در محاسبهٔ تقسیم چندجملهایها کمک میکرد. ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با تقسیم چند جمله ای ها نهم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





عالی بود من کاملا یاد گرفتم
با سلام دوست عزیز
خدا راذسپاس که مفید واقع شده
خیلی عالی و دقیق توضیح دادید من کامل فهمیدم
مرسی و ممنون از زحمت شما خیلی خوب بود
واقعا عالي و كامل بود خيلي خوب متوجه شدم
عالی خوب متوجه شدم
با سلام
خدا رو شکر
وای عالی بوددد بالاخره یجا خوب توضیح دادن
با سلام تخصص ما تدریس به زبان ساده وآسان است
خوب بود
بد نبود
عالی
سلام ما از کجا بدونیم توی سوالات باید تقسیمارو کسری بنویسیم ساده کنیم یا چکشی بنویسیم حل کنیم؟ چون با دوروش میشه تقسیمارو انجام داد