آموزش ریاضی پایه هفتم
محاسبه حجم های منشوری هفتم 💎📏 – سریع و آسان!
در درسنامۀ محاسبه حجم های منشوری هفتم قصد داریم تا روش به دست آوردن حجم یک منشور را بررسی کنیم. برای این کار، ابتدا آنچه که برای محاسبۀ حجم یک مکعب مستطیل انجام دادیم، مرور میکنیم. از همان روشی که برای مکعب مستطیل به کار بردیم، برای محاسبۀ حجم منشور نیز استفاده میکنیم. در انتها نیز، مثالهای متنوعی از محاسبۀ حجم منشورها با قاعدههای مختلف حل خواهیم کرد. پیشنهاد میکنیم قبل از مطالعۀ این درسنامه، درسنامۀ حجم های هندسی ریاضی هفتم را مرور کنید.
چگونه حجم یک منشور را محاسبه کنیم؟
پیش از این روش محاسبۀ حجم دو نوع منشور را میدانستیم؛ یکی مکعب و دیگری مکعب مستطیل. مکعب، منشوری با قاعدۀ مربع است و مکعب مستطیل، منشوری با قاعدۀ مستطیل است. مشابه همان روشی که حجم یک مکعب مستطیل را محسابه کردیم، میتوانیم حجم یک منشور دلخواه را نیز محاسبه کنیم. بنابراین، در قسمت بعدی از درسنامۀ محاسبه حجم های منشوری هفتم مروری میکنیم بر آنچه که برای محاسبۀ حجم مکعب مستطیل انجام دادیم.
یادآوری از مکعب مستطیل
خاطرتان هست که برای محاسبۀ حجم یک مکعب مستطیل، طول را ضرب در عرض ضرب در ارتفاع میکریم. اگر به مکعب مستطیل به شکل یک منشور نگاه کنیم، ارتفاع آن همان یال آن است (در صورتی که فراموش کردهاید یال چیست، درسنامۀ حجم های هندسی ریاضی هفتم را مرور کنید) و حاصل ضرب طول ضرب در عرض، مساحت قاعدۀ آن را به ما میدهد. به شکل زیر نگاه کنید:

بنابراین برای محاسبۀ حجم یک مکعب مستطیل، مساحت قاعدۀ آن را ضرب در اندازۀ یال آن میکردیم. اما این کار ما چه دلیلی داشت؟ در واقع محاسبۀ حجم یک جسم معادل است با محاسبۀ تعداد مکعبهای به ضلع واحد که درون آن جسم میگنجند. باتوجه به این نکته بیایید در قسمت بعدی از درسنامۀ محاسبه حجم های منشوری هفتم محاسبه کنیم.
مثال از محاسبة حجم مکعب مستطیل
فرض کنید می خواهیم حجم یک مکعب مستطیل با ابعاد زیر را محاسبه کنیم:
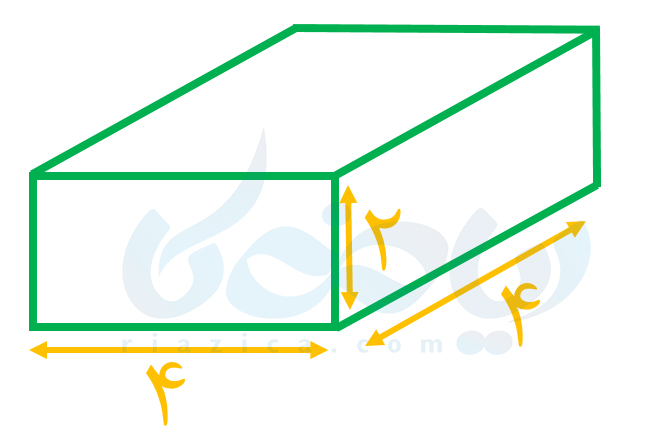
مکعب مستطیل بالا را میتوانیم به صورت زیر به مکعبهای با حجم واحد تقسیم کنیم:
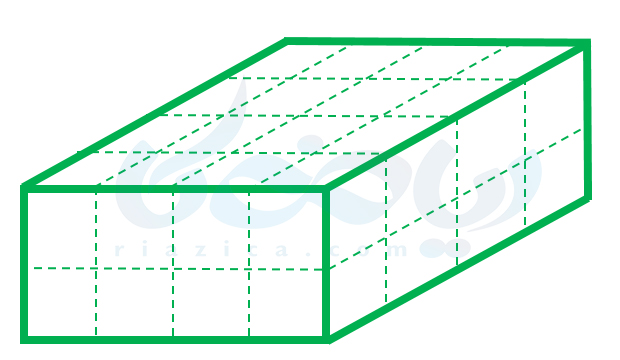
حالا بیایید تعداد مکعبهای کوچک را در شکل بالا محاسبه کنیم. برای این کار میتوانیم مکعب مستطیل را به \(\Large 4\) لایه به شکل زیر تقسیم کنیم (هر لایه را با یک رنگ هاشور زدهایم):
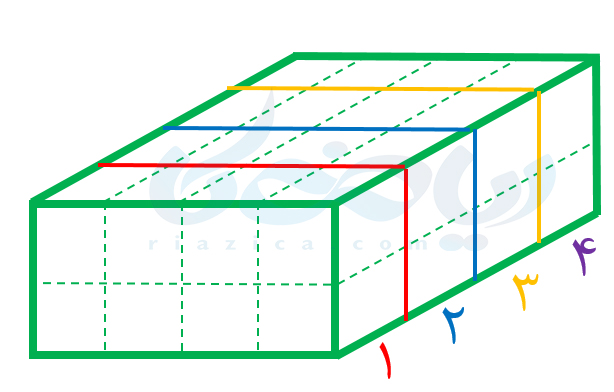
اگر تعداد مکعبهای یک لایه را بشماریم و ضرب در تعداد لایه ها که همان \(\Large 4\) است بکنیم، تعداد کل مکعبهای کوچک و در نتیجۀ آن، حجم مکعب مستطیل به دست میآید. لایۀ \(\Large 1\) را به شکل زیر به صورت جدا در نظر میگیریم تا مکعبهای آن را بشماریم:
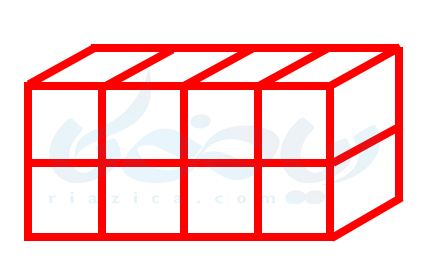
تعداد مکعبهای لایۀ \(\Large 1\) برابر است با تعداد مربعهای با مساحت واحد که سطح لایۀ \(\Large 1\) را پوشانده است؛ یعنی تعداد مکعبهای لایۀ \(\Large 1\) برابر است با \(\Large 4 \times 2\). حال کافی است این مقدار را در تعداد لایهها که برابر با \(\Large 4\) تا بود ضرب کنیم. در نتیجه تعداد مکعبهای کوچک درون مکعب مستطیل که برابر با حجم مکعب مستطیل است، برابر است با \(\Large (4 \times 2) \times 4\). حال اگر دقت کنید میبینید که عدد \(\Large 4\) که در رابطۀ قبل خارج از پرانتز نوشته شده همان اندازۀ یال مکعب مستطیل و حاصل ضرب \(\Large 4 \times 2\) درون پرانتز، همان مساحت قاعدۀ مکعب مستطیل است. در قسمت بعدی از درسنامۀ محاسبه حجم های منشوری هفتم از مثالی که حل کردیم نتیجه گیری میکنیم.
رابطۀ حجم یک منشور
همین کاری را که برای مکعب مستطیل انجام دادیم، میتوانیم برای محاسبۀ حجم منشورهای دیگر نیز انجام دهیم. یعنی مساحت قاعدۀ آنها را در طول یال آن ها ضرب کنیم. بنابراین اگر حجم منشور را با \(\Large V_p\)، مساحت قاعدۀ آن را با \(\Large S\) و ارتفاع آن را با \(\Large h\) نشان دهیم، داریم:
\(\LARGE V_p=S \times h\)
به قسمت بعدی از درسنامۀ محاسبه حجم های منشوری هفتم توجه کنید.
مثال از محاسبۀ حجم منشور
در این قسمت، حجم منشورها با قاعدههای مختلف را محاسبه خواهیم کرد. در اولین مثال، حجم یک استوانه که در واقع همان منشور با قاعدۀ دایره است را به دست میآوریم.
محاسبۀ حجم استوانه
مثال 1: حجم استوانۀ زیر را محاسبه کنید.
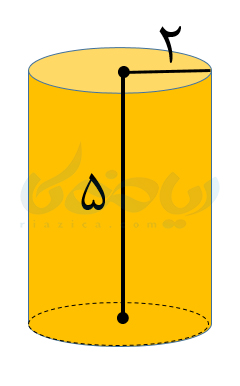
حل: همان طور که گفتم، استوانه یک منشور با قاعدۀ دایره است. بنابراین برای به دست آوردن حجم استوانه کافی است مساحت قاعدۀ آن که یک دایره است را در ارتفاع (یال) آن ضرب کنیم. اگر مساحت قاعدۀ استوانه را با \(\Large S_c\) نشان دهیم، داریم:
\(\LARGE S_c=\pi \times r \times r=4 \pi\)
بنابراین حجم استوانۀ داده شده برابر است با:
\(\LARGE V_c=4 \pi h=20 \pi\)
به مثال بعدی از درسنامۀ محاسبه حجم های منشوری هفتم توجه کنید.
محاسبۀ حجم منشور با قاعدۀ مثلث
مثال 2: حجم منشور سه وجهی زیر را محاسبه کنید.
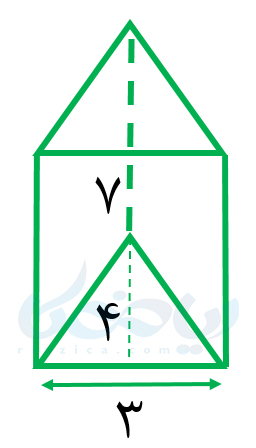
حل: همان طور که گفتیم، باید مساحت قاعده را در اندازۀ یال منشور ضرب کنیم. اگر مساحت قاعدۀ منشور را با \(\Large S_p\) نشان دهیم، داریم:
\(\LARGE S_p=\frac{3 \times 4}{2}=6\)
بنابراین حجم منشور داده شده برابر است با:
\(\LARGE V_p=6 \times 7=42\)
به مثال بعدی از درسنامۀ محاسبه حجم های منشوری هفتم توجه کنید.
مثال از محاسبه حجم های منشوری هفتم
مثال 3: حجم منشور زیر را محاسبه کنید.
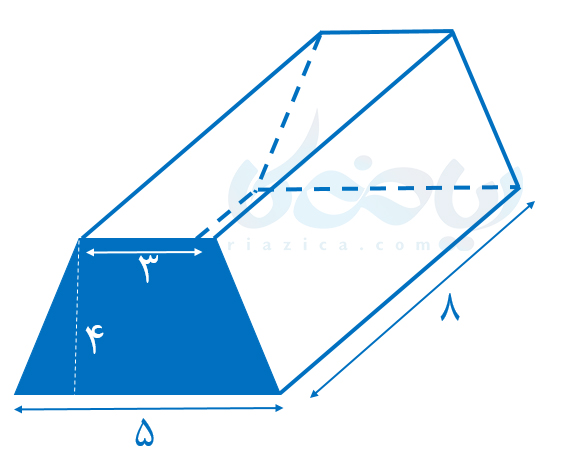
حل: قاعدۀ منشور ذوزنقه است. همان طور که به خاطر دارید، مساحت ذوزنقه از رابطۀ زیر به دست می آید:

بنابراین اگر مساحت قاعدۀ منشور را با \(\Large S_p\) نشان دهیم، داریم:
\(\LARGE S_p=\frac{(3+5) \times 4}{2}=16\)
بنابراین حجم منشور داده شده برابر است با:
\(\LARGE V_p=16 \times 8=128\)
به مثال بعدی از درسنامۀ محاسبه حجم های منشوری هفتم توجه کنید.
مثال از محاسبه حجم های منشوری هفتم
مثال 4: حجم منشور زیر را محاسبه کنید.
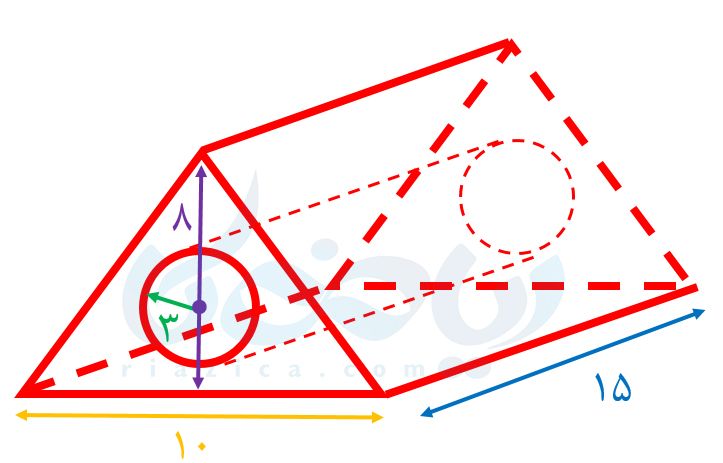
حل: همان طور که در شکل بالا مشاهده میکنید، یک منشور سه وجهی داریم که یک استوانه از آن کم شده است. برای پیدا کردن حجم منشور داده شده، میتوانیم از یکی از دو روش زیر استفاده کنیم:
- مساحت دایره را از مساحت مثلث کم کنیم و حاصل را در اندازۀ یال منشور ضرب کنیم.
- حجم منشور را بدون در نظر گرفتن استوانه حساب کنیم. حجم استوانه هم حساب کنیم. تفاضل دو مقدار به دست آمده، حجم را به ما میدهد.
از روش اول استفاده میکنیم. اگر مساحت مثلث را با \(\Large S_t\) و مساحت دایره (قاعدۀ استوانه) را با \(\Large S_c\) نشان دهیم، داریم:
\(\LARGE S_t=\frac{10 \times 8}{2}=40\)
\(\LARGE S_c=\pi \times 3 \times 3=9 \pi\)
اگر مقدار عدد \(\Large \pi\) را برای ساده شدن محاسبات به صورت تقریبی برابر با \(\Large 3\) در نظر بگیریم، داریم:
\(\LARGE S_c=9 \pi \approx 27\)
\(\LARGE \Rightarrow S_t-S_c=40-27=13\)
بنابراین، برای به دست آوردن حجم منشور کافی است عدد \(\Large 13\) را در اندازۀ یال ضرب کنیم:
\(\LARGE V_p=13 \times 15=195\)
دوستان ریاضیکا قبل خوندن این پست ،پست حجم های هندسی ریاضی هفتم را مطالعه کنید ودر ادامه پست مساحت جانبی وکل ریاضی هفتم را بخوانید.
زنگ آخر کلاس محاسبه حجم های منشوری هفتم
در درسنامهای که از ریاضی هفتم خواندیم، ابتدا با استفاده از روشی که برای محاسبۀ حجم یک مکعب مستطیل استفاده میکریم، رابطهای برای محاسبۀ حجم یک منشور دلخواه به دست آوردیم. همان طور که دیدیم، حجم یک منشور از حاصل ضرب مساحت قاعدۀ آن در اندازۀ یال آن به دست می آید. در انتهای درسنامه، حجم منشورهای مختلف با قاعده های دلخواه (از جمله استوانه که منشوری با قاعدۀ دایره است) را به دست آوردیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با این مبحث دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





واقعاً فوق العاده بود?
با سلام واحترام
ممنون از شما دوست عزیز
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
عالی بودش
با سلام
ممنون دوست گرامی
خیلی عالی و جامع بود ،. ممنون??
با سلام وعرض ادب
ممنون از نظر مثبت وپر مخبت شما
اصلا نفهمیدم اوکی عالی بود????
با سلام واحترام
کجا رو متوجه نشدید؟
سلام خوبی سه حجم منشوری حجم های هرمی. حجم های کروی توضییح دهید
سلام من فرپول حجم مکعب مستطیل رو متوجه نشدم!!!!!
ببخشید فرمول*
با سلام واحترام
حجم مکعب مستطیل میشود طول ضربدر عرض ضربدر ارتفاع
V=s×h
حجم منشور=مسحت قاعده×ارتفاع
با سلام
ممنون از پاسخگویی شما
سلام
عالی
با سلام ووقت به خیر
ممنون دوست گرامی
با سلام مطالب خیلی تاثیر گذار بود ممنون
با سلام وعرض ادب
میتونید با تهیه دوره آموزشی هشتم از آموزشهای بیشتر بهتر کا بهرمند باشید
با سلام تورو خدا جواب بدید
حجم یک منشور 100cm و مساحت قاعده آن 25cm است
ارتفاع این منشور چند سانتی متر است با توضیح ممنونم
با سلام
کافیه حجم رو به مساحت قاعده تقسیم کنید که میشه ۴
عالی
با سلام
ممنون از نگاه شما
سوال (حجم هر منشور برابر است با…………….) جای خالی چی میشه؟
مساحت دایره ×ارتفاع
(: دمت گرم
ستونی داریم به شکل ۶ظلعی منتظم که ارتفاع ۱۵ و هر ضلع ۶ضلعی بدنه این ستون را کاشی کاری کنیم چند متر مربع کاشی باقی میماند؟
سلام وقت بخیر میشه یکی جواب اینو بهم بگه
۶×6=۳۶
۳۶×۱۵=جواب
بی نظیر بود، ممنون
با سلام وادب
ممنون از انرژی که به ما میدهید
مرسی از کسی که این رو نوشته من امسال و سال دیگه این رو خیلی نیاز دارم
مرسی از کسی که این رو نوشته
عالیییی بود لطفا بیشتر بفرستید
با سلام
ما تمام درسهای ریاضی پایه هفتم رو نوشتیم
عالی
با سلام و ادب
ممنون از نگاه شما
سلام با عرض ادب اگر میشه حجم ذوزنقه رو بگید
مجموع دوقطر ضربدر ارتفاع تقسیم بر دو
عالییییی بود
سلام ممنون از شما