آموزش ریاضی پایه هفتم
حجم های هندسی ریاضی هفتم 📚🎁 – خوب بشناسشون!
در درسنامۀ حجم های هندسی ریاضی هفتم ابتدا حجمها را به دو دوستۀ هندسی و غیر هندسی تقسیم میکنیم. سپس، از بین حجمهای هندسی، حجمهای منشوری را معرفی کرده و روش نامگذاری اجزای آن را بررسی میکنیم. در انتهای درسنامه نیز، مقطع زدن و دید از بالا به یک منشور را مورد بررسی قرار میدهیم. با ما تا انتهای درسنامۀ حجم های هندسی ریاضی هفتم همراه باشید.
حجم های هندسی و غیر هندسی
میتوان حجمها را به دو دستۀ هندسی و غیر هندسی تقسیم کرد. به حجمهایی که در یکی از سه دستۀ زیر قرار داشته و یا از ترکیبی از آنها تشکیل شده باشند، حجم های هندسی میگوییم.
- حجم های منشوری
- حجم های کروی
- حجم های هرمی
به حجمهایی که در سه دستۀ بالا قرار نداشته باشند و یا از ترکیبی از آنها تشکیل نشده باشند،حجم های غیر هندسی میگوییم. درادامۀ درسنامۀ حجم های هندسی ریاضی هفتم انواع حجم های هندسی را بررسی میکنیم.
حجم های منشوری
مثال 1: حجمهای زیر، حجم های منشوری هستند:
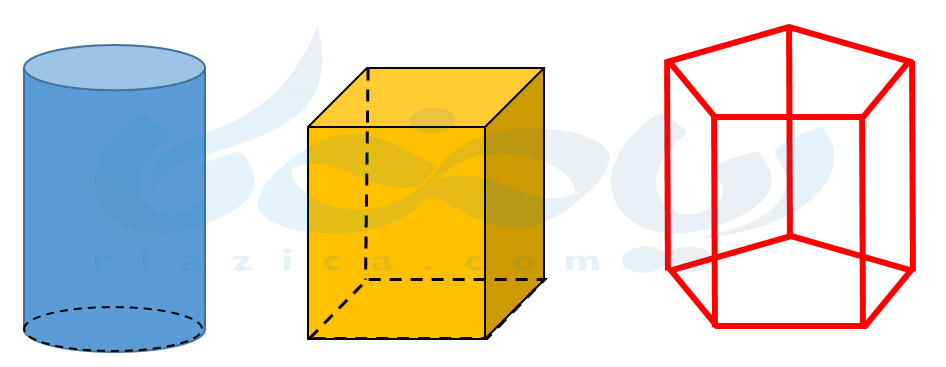
اگر دقت کنید میبینید که حجمهای منشوری بین دو سطح موازی قرار گرفتهاند. در مکعب، این دو سطح موازی، دو مربع هستند. در استوانه، دو سطح موازی، دو دایره هستند. با تغییر این دو سطح موازی میتوان حجم های منشوری مختلف به دست آورد. در ادامۀ درسنامۀ حجم های هندسی ریاضی هفتم اجزای حجم های منشوری را نامگذاری میکنیم.
نامگذاری اجزای حجم های منشوری
همان طور که گفتیم، حجم های منشوری بین دو سطح موازی قرار دارند. به این دو سطح موازی، دو قاعدۀ منشور میگوییم. هر سطحی به غیر از این دو قاعده را وجه های جانبی منشور میگوییم. محل اتصال (اشتراک) وجه های جانبی با یکدیگر و یا با قاعده های منشور را یال های منشور مینامیم. محل اتصال (اشتراک) یال ها با قاعدهها را نیز، رأس های منشور مینامیم. در منشور زیر، رأسها، یالها و قاعدههای منشور را مشخص کردهایم:
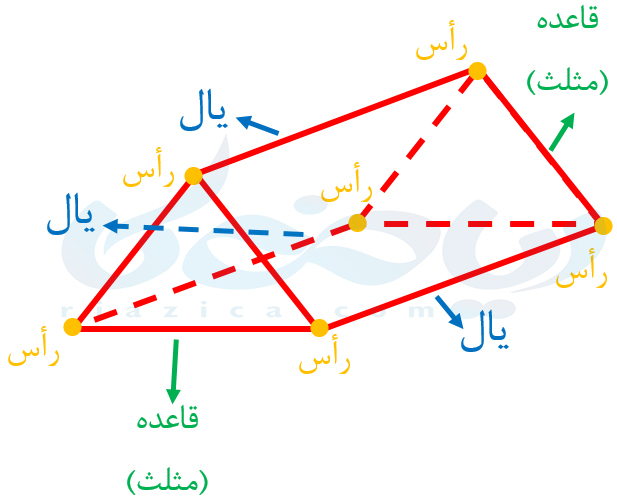
وجههای جانبی منشور بالا نیز سه متوازی الاضلاع هستند. برای اینکه بهتر متوجه شوید، در مثالهای بعدی از درسنامۀ حجم های هندسی ریاضی هفتم اجزای منشور را نام گذاری میکنیم.
مثال ازحجمهای منشوری
مثال 2: در شکل زیر، قاعدهها، وجههای جانبی، یالها و رئوس منشور را مشخص کنید.
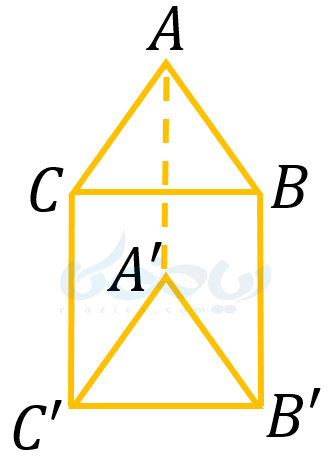
حل: اصطلاحاً به منشور شکل بالا، منشور سه پهلو میگوییم. زیرا دارای سه وجه جانبی است. قاعده های منشور شکل بالا، مثلثهای \(\Large ABC\) و \(\Large A’B’C’\) هستند. وجه های جانبی آن، مستطیلهای \(\Large ABB’A’\) و \(\Large BCC’B’\) و \(\Large CAA’C’\) هستند. یال های این منشور، پارهخطهای \(\Large AA’\) و \(\Large BB’\) و \(\Large CC’\) و رئوس این منشور، نقاط \(\Large A\) و \(\Large B\) و \(\Large C\) و \(\Large A’\) و \(\Large B’\) و \(\Large C’\) هستند. همان طور که دیدید برای نامگذاری اجزای این منشور از یک نظم خاص پیروی کردیم. همان طور که در درسنامۀ راهبردهای حل مسئله ریاضی هفتم گفتیم، به این رویکرد منظم حل مسئله، راهبردالگوسازی میگوییم.
مثال از درسنامۀ حجم های هندسی ریاضی هفتم
مثال 3: قاعدهها، وجههای جانبی، یالها و رئوس منشور زیر را مشخص کنید.
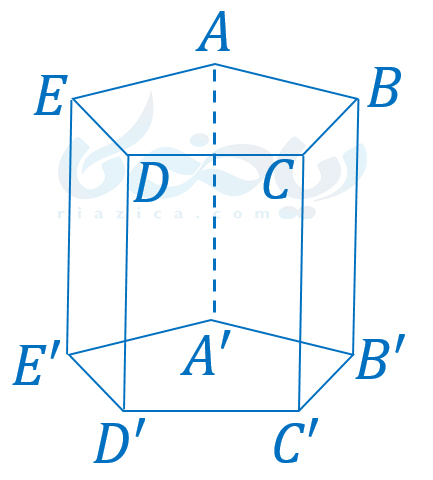
حل: اصطلاحاً به منشور شکل بالا، منشور پنج پهلو میگوییم. زیرا دارای پنج وجه جانبی است. قاعده های منشور شکل بالا، پنج ضلعیهای \(\Large ABCDE\) و \(\Large A’B’C’D’E’\) هستند. وجه های جانبی آن، مستطیلهای \(\Large ABB’A’\) و \(\Large BCC’B’\) و \(\Large CDD’C’\) و \(\Large DEE’D’\) و \(\Large EAA’E’\) هستند. یال های این منشور، پارهخطهای \(\Large AA’\) و \(\Large BB’\) و \(\Large CC’\) و \(\Large DD’\) و \(\Large EE’\) و رئوس این منشور، نقاط \(\Large A\) و \(\Large B\) و \(\Large C\) و \(\Large D\) و \(\Large E\) و \(\Large A’\) و \(\Large B’\) و \(\Large C’\) و \(\Large D’\) و \(\Large E’\) هستند.
در قسمت بعدی از درسنامۀ حجم های هندسی ریاضی هفتم به بررسی حجم های هرمی میپردازیم.
حجم های هرمی
مثال 4: حجمهای زیر هرمی هستند:
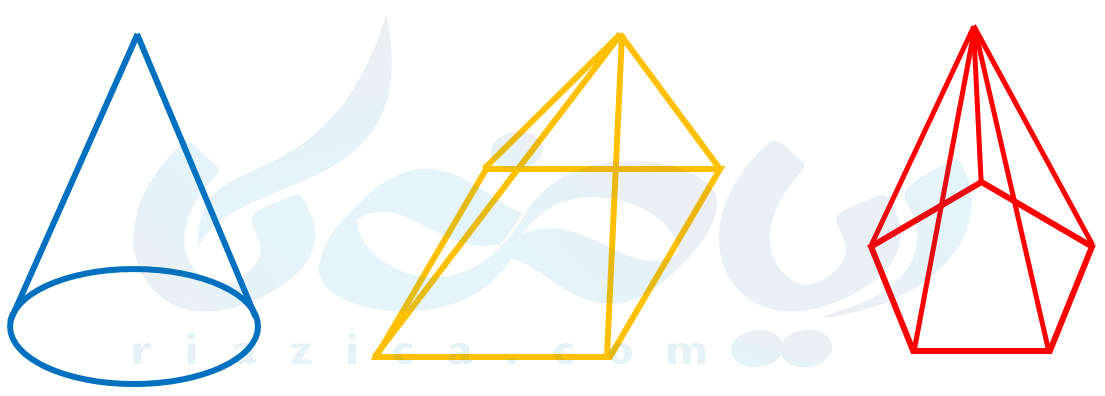
حجم های هرمی بین یک سطح (قاعده) و یک نقطه قرار دارند. قاعدۀ یک هرم میتواند هر شکلی باشد. قاعدۀ هرمهای شکل بالا از راست به چپ، پنج ضلعی منتظم، متوازی الاضلاع و دایره است. به طور خاص، مخروط، هرمی با قاعدۀ دایره است.
حجم های کروی
مثال 5: حجم زیر، حجم کروی است:

شکل کروی شکلی است که مجموعه نقاط آن در فضای سه بعدی، از یک نقطۀ ثابت به یک اندازه است. حجم چنین شکلی، حجم کروی است. در ادامۀ درسنامۀ حجم های هندسی ریاضی هفتم مثالهایی از حجمهای هندسی ترکیبی خواهیم دید.
حجم های هندسی ترکیبی
همان طور که در معرفی حجم های هندسی گفتیم، برخی از حجم های هندسی نیز از ترکیب تعدادی از سه دستهای که گفتیم، یعنی حجمهای منشوری، حجمهای هرمی و حجمهای کروی، به وجود میآیند.
مثال 6:حجمهای زیر، ترکیبی هستند:
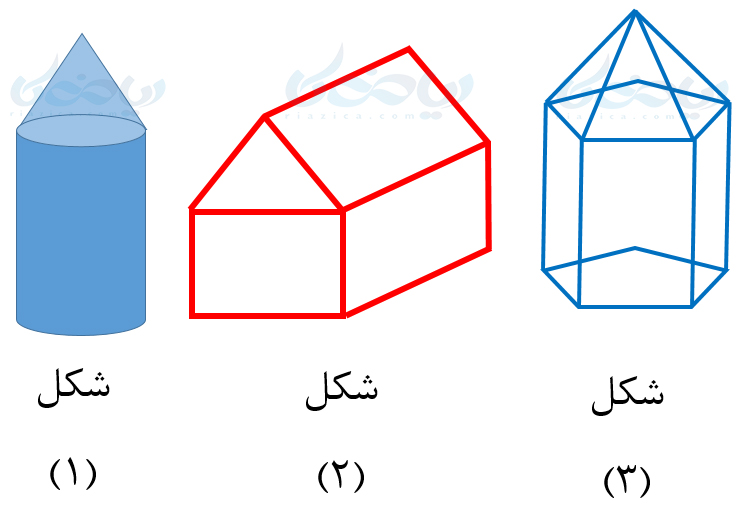
حجم اول از ترکیب یک استوانه (حجم منشوری) و یک مخروط (حجم هرمی) تشکیل شده است. حجم دوم از ترکیب یک مکعب (حجم منشوری) و یک حجم منشوری با قاعدۀ مثلث به وجود آمده است. حجم سوم نیز از ترکیب یک حجم منشوری با قاعدۀ پنجضلعیمنتظم و یک حجم مخروطی با قاعدۀ پنجضلعیمنتظم به وجود آمده است. به قسمت بعدی از درسنامۀ حجم های هندسی ریاضی هفتم توجه کنید.
مقطع زدن
در صورتی که یک شکل در فضای سه بعدی را با یک صفحه قطع کنیم، به اصلاح کتاب درسی میگوییم مقطع زده ایم. مثلاً در شکل زیر، یک صفحۀ موازی با قاعدۀ استوانه، استوانه را قطع کرده است:

همان طور که میبینید، سطح مقطع این برش، یک دایره است. اگر یک صفحۀ مایل (کج)استوانه را قطع میکرد، سطح مقطع مانند شکل زیر یک بیضی میشد:

در تصویر متحرک زیر نیز میتوانید آنچه در دو شکل بالا نشان دادیم، مشاهده کنید:
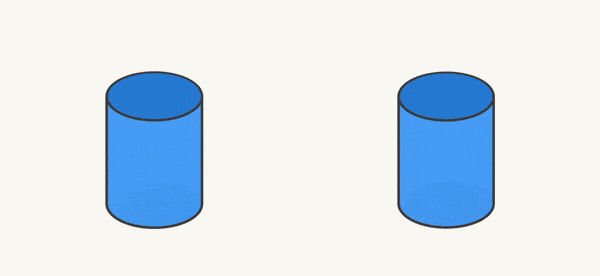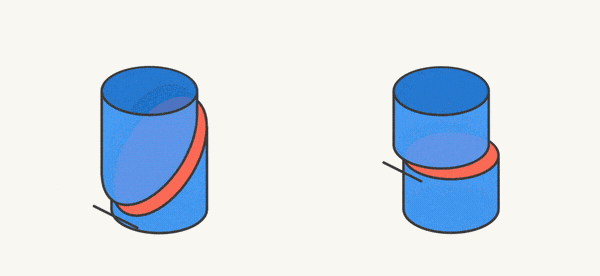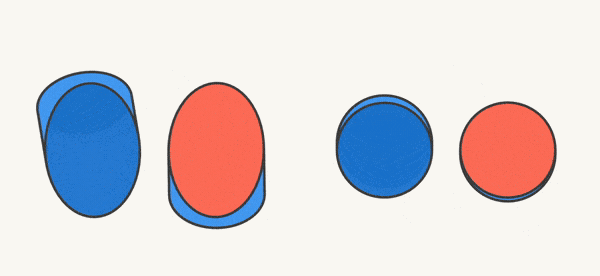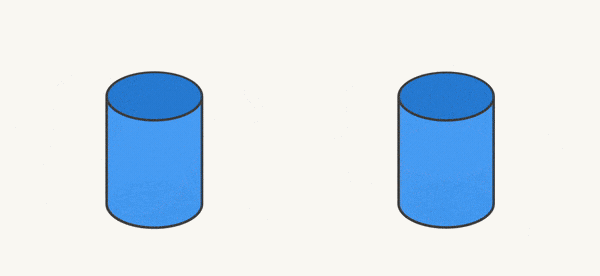
البته همین کار را برای شکلهای دیگری غیر از استوانه نیز میتوانیم انجام دهیم. مثلاً در شکل زیر، یک مکعب را با یک صفحه قطع کردهایم (برش دادهایم):
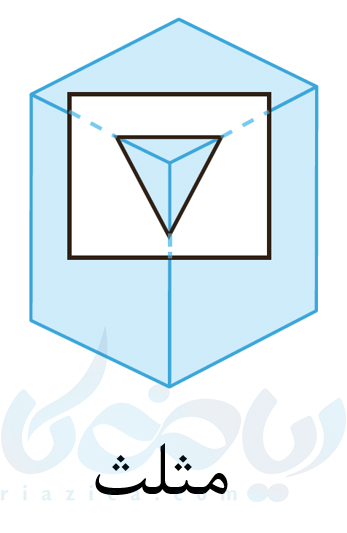
همان طور که میبینید، سطح مقطع، یک مثلث شده است. بین اشکال مختلف، به طور خاص، مقاطع مخروطی اهمیت ویژهای برای ما دارند و در سالهای آینده به آنها خواهیم پرداخت. در قسمتی بعدی از درسنامۀ حجم های هندسی ریاضی هفتم دید از بالا را بررسی میکنیم.
دید از بالا
میتوان به اشکال مختلف در فضای سه بعدی، از جهات مختلف نگاه کرده و شکل دو بعدیشان را رسم نمود. در واقع به این صورت، تصویر یک شکل سه بعدی را در فضای دو بعدی به دست میآوریم. مثلاً به منشور زیر از بالا نگاه کنید:
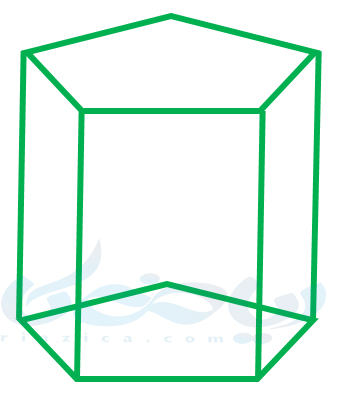
دید از بالای آن، شکل زیر خواهد شد که همان قاعدۀ منشور است:

همین کار را برای دید در زوایای دیگر و همچنین برای اشکال مختلف نیز میتوان انجام داد.
توصیه میشه برای یادگیری محاسبه حجم منشورها پست محاسبه حجم منشوری هفتم را مطالعه کنید.
زنگ آخر کلاس حجم های هندسی ریاضی هفتم
در درسنامه حجم های هندسی ریاضی هفتم که از ریاضی هفتم خواندیم، ابتدا تعریف حجم های هندسی و غیر هندسی را دیدیم. سپس، حجم های منشوری، هرمی و کروی را بررسی کرده و به طور خاص اجزای حجم های منشوری را نام گذاری کردیم. در قسمت آخر درسنامه نیز، تعریف مقطع زدن و همچنین مفهوم دید از بالا به یک منشور را مورد بررسی قرار دادیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با این مبحث دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





کتاب ریاضیحجم منشوری
با سلام وعرض ادب
متوجه منظور شما نشدیم
خیلی عالی بود مرسی
ممنون دوست عزیز
منم
خیلی ممنون
سلام و عرض ادب
ممنون از انرژی و پیام پرمهرتون.
موفق باشید.
پیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
خیلی عالی و جامع و کامل بود. برای فصل ۵ ریاضی ششم هم می خوره.
عالی بود
آیا فرمول حجم برای تمام منشور ها استفاده میشه؟ sقاعده×h
با سلام وعرض ادب
ممنون از شما بل دستور حجم همه منشورها همونه
سلام ببخشید صندلی یه حجم هندسیه؟
سلام وعرض ادب
خیر
سلام اساتید عزیز
ممنون از این همه وقتی که در اختیار توضیح کامل درس ها قرار میدهید تا ما خوب متوجه شویم❤
فکر کنم صحبتم در این topic جایگاه مناسبی نداشته باشه ولی به هر حال…
اگر میشه مطلبی در مورد فصل ۸ ریاضی نهم (حجم و مساحت کره ، حرم ، مخروط و…) را هم قرار دهید با سپاس
با سلام واحترام
ممنون از شما دوست عزیز فصل هشتم نوشته شده به زودی بارگذاری میشه
سلام دوست عزیز به این دسته بندی مراجعه کنhttps://riazica.com/category/9th-grade-math/
سلام ممنونم بابت متن علمی و باارزشتون
خواستم بگم سیب چه نوع حجمی است؟
سلام و وقت به خیر
شبیه کره هست
ولی غیر هندسی می باشد
سلام واقعا ازتون ممنونم این فصل رو خیلی عالی و خوب تدریس کردین از همه ی دست در کاران تشکر میکنم
با سلام واحترام
ممنون از شما نظرات شما مایه دلگرمی ماست
سلام
یه شکلی که منشوری هست و از پایین یک نیم دایره ازش کم شده و ارتفاع شکل منشوری ۹_قائده ۱۰_و طول ۸این رو چجوری حساب میکنیم؟
3/ 11/ 1402
سلام اگه فیلم بود بهتر بود
ولی خدایی خوب بود
با سلام وادب
ممنون از نگاه شما
ممنون از شما
باسلام ببخشید میشه چند نمونه از اشکال هندسی و غیر هندسی در زندگی روز مره را نام ببرید نیاز دارم لطفا هرچی سریعتر پاسخ بدین
ممنون میشم
سلام میشه چند نمونه شکل هندسی و غیر هندسی در زندگی روز مره نام ببرید ممنون میشم
خیلی خوب بود کامل یاد گرفتم ممونم از تدریس خوبتون❣
با سلام وادب
خوشحالیم که مفید واقع شده
خوب بود ولی مسئله نداشت
عالی
با سلام وادب
ممنون دوست عزیز
با سلام ممنون از نگاه شما
الووو
بفرمایید
خیلی خوب
خیلی خوب بود ممنون
دوچرخه چه نوع حجمی است؟
با سلام حجمهایی که منشوری یا کروی یا هرمی نباشند غیر هندسی هستند پس دوچرخه غیر هندسی است
عالی
سپاس دوست عزیز
عالی
سلام
خیلی ممنون از تدریس خوبتون
عالی بود
سلام و خسته نباشید . خیلی ممنون عالی بود
سلام واقعا خیلی ممنونم ببخشید فرمول همهی اشکال هندسی رو میزارید ممنون خیلی 💜💜💜💜
خیلی خوب بود ممنون
ببخشید دوره محاسبات سریع به چه نوع هست؟ آنلاین؟ فیلم ضبط شده یا…؟ و چجوری به دستمون میرسه؟
سلام دوست عزیز
به صورت فیلم ضبط شده هست وقتی پرداخت انجام میشه از روی سایت دانلود می کنید
من چی میگم تو چی میگی
سلام دوست عزیز شما دقیقا چی میگید
خوب بود
با سلام ممنون از نظر شما
3/ 11/ 1402
خیلی خوب بود
با سلام وادب
ممنون از لطف شما
خوب
آیا کره وجه دارد ؟؟
با سلام خیر سطح دارد
خیر
سلام ویژگی منشور مکعب چند مورد توضیح بدید در پایه هفتم ممنون
i hait mahs
عالی بود