آموزش ریاضی پایه یازدهم تجربی، آموزش هندسه دهم ریاضی
تشابه مثلث ها و اثبات بوسیله قضیه تالس 🎢🔺 – یک اصل مهم در ریاضی دهم
مفهوم دیگری که در فصل دوم کتاب ریاضی یازدهم تجربی بیان شده است در مورد تشابه مثلث ها است. این مفهوم به سادگی با کمک قضیه تالس قابل اثبات است. تشابه مثلث ها مفهومی مهم و کاربردی است که در ادامه با آن بیشتر آشنا میشویم.
در پست آموزش مثلثات و نسبتهایش خواندید دو مثلث وقتی با هم متشابهاند که تمام زاویه های نظیر به نظیرشان با هم برابر باشند. در مثلثهای متشابه اضلاع متناظر نیز با هم تناسب دارند. وقتی میگوییم مثلث ABC و ‘A’B’C با هم متشابهاند که:
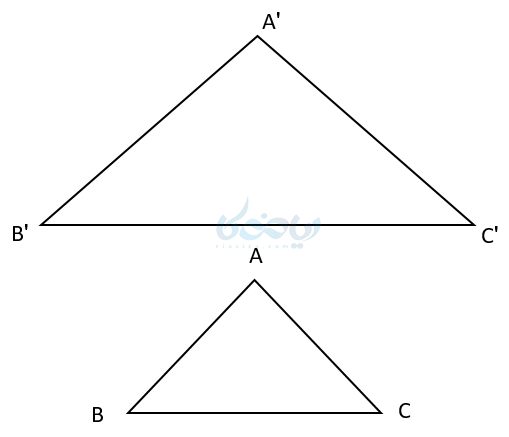
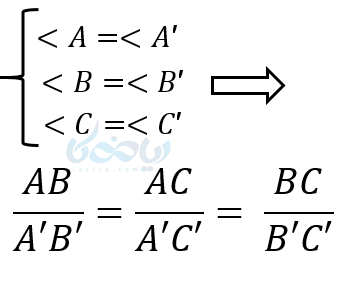
زمانیکه شما بر روی شکلی در گوشی یا رایانه خوتان زوم میکنید، در اصل شکلی متشابه با آن شکل را می بینید که اضلاع آن به یک تناسب بزرگ شدهاند. و نکته مهم اینجاست که اندازه زاویه ها تغییر نکرده است.
قضیه اساسی تشابه مثلث ها به کمک قضیه تالس
صورت قضیه :
اگر خطی موازی یکی از اضلاع مثلث دو ضلع دیگر را قطع کند، در این صورت مثلث کوچکی که به وجود میآید با مثلث بزرگ اولیه متشابه است.
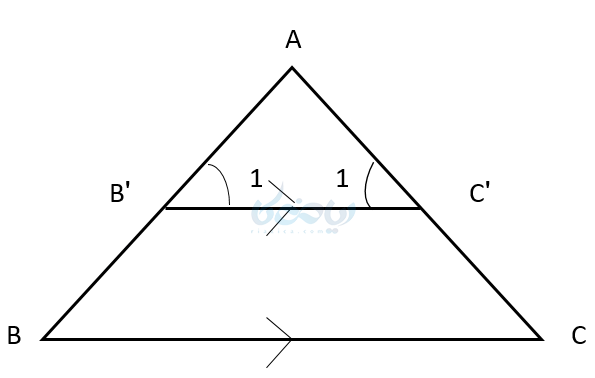
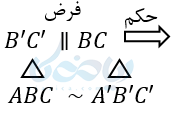
اثبات :
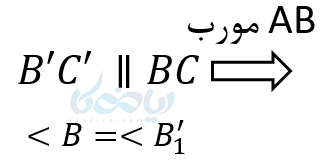
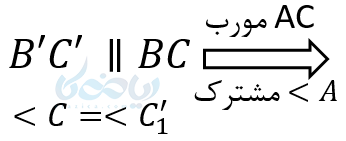
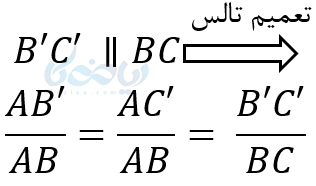
پس زاویه ها مساوی واضلاع متناسب هستند. در نتیجه مثلثها متشابهاند:
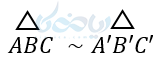
با استفاده از قضیه اساسی تشابه میتوان قضیههای زیر را بیان و اثبات کرد. البته اثبات آنها مدنظر کتاب ریاضی پایه یازدهم تجربی نیست. اما ما در اینجا اثبات این قضیههای مهم تشابه را برایتان بیان میکنیم. با استفاده از آنها و با داشتن اندازه بعضی از اضلاع و یا زاویهها، میتوان به تشابه مثلث ها پی برد.
قضایای تشابه مثلث ها واثبات آنها
قضیه 1: هرگاه دو زاویه از دو مثلث با هم برابر باشند، آن دو مثلث با هم متشابهاند.
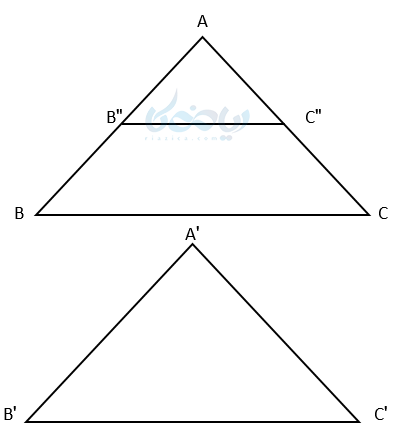
اثبات ۱:
فرض وحکم به صورت زیر است:
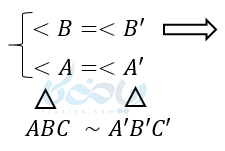
چون دو زاویه این دو مثلث برابرند پس زاویه سوم نیز برابر است.
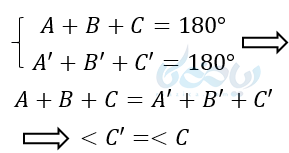
برای اثبات این قضیه با اندازه ‘A’B روی AB جدا می کنیم و آن را “AB مینامیم. به اندازه ی ‘A’C روی AC جدا کرده و آن را نیز “AC نامگذازی میکنیم. “B را به “C وصل میکنیم. دو مثلث ‘A’B’C و “A”B”C بایکدیگر همنهشت هستند، زیرا :
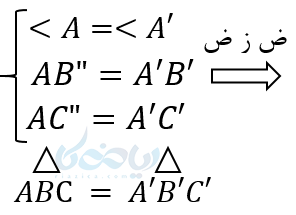
از طرفی :
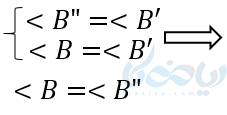
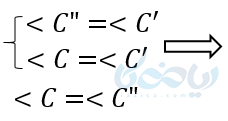
پس نتیجه میگیریم طبق قضیه توازی BC با “B”C موازی است. در نتیجه طبق قضیه اساسی، دو مثلث ABC و”AB”Cمتشابه هستند. از طرفی چون دو مثلث “AB”C و ‘AB’C با یکدیگر برابرند، پس طبق اصل تشابه مثلث ها دو مثلث ABC و ‘A’B’C نیز متشابه هستند.
قضیه 2:
هرگاه دو ضلع از دو مثلث با هم متناسب و زاویه بین دو ضلع از دو مثلث برابر باشند، آنگاه دو مثلث متشابهاند.

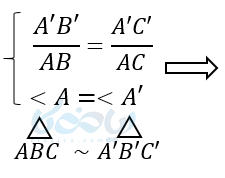
اثبات ۲: برای اثبات این قضیه روی ضلع AB به اندازه ‘A’B جدا میکنیم تا “AB به وجود آید. روی AC نیز به اندازه ‘A’C جدا میکنیم تا “AC به وجود آید. همچنین از “B به “C وصل میکنیم. دو مثلث “A”B”C و ‘A’B’C با هم برابرند. زیرا:

در فرض داشتیم:
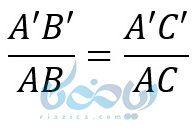
در این تناسب به جای ‘A’B و ‘A’C دو ضلع “AB و “AC را جایگذاری میکنیم و خواهیم داشت:

از طرفی میدانیم:
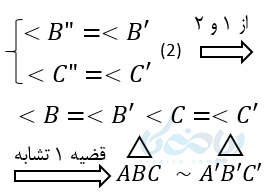
قضیه 3 تشابه مثلث ها:
اگر سه ضلع از مثلثی با سه ضلع از مثلث دیگر متناسب باشند آن دو مثلث متشابه هستند.

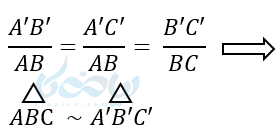
روی ضلع AB به اندازه ‘A’B جدا میکنیم. پس ‘AB” = A’B و آن را “B مینامیم . سپس “B”C را موازی BC را رسم میکنیم . در نتیجه خواهیم داشت:
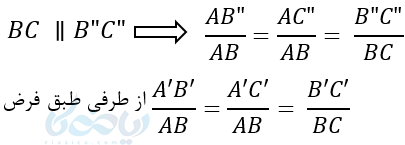
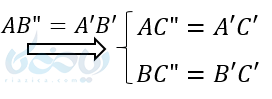
پس دو مثلث “A”B”C و ‘A’B’C با هم به حالت سه ضلع برابرند.

از طرفی چون BC با “B”C موازی است پس طبق قضیه توازی داریم:
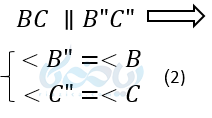
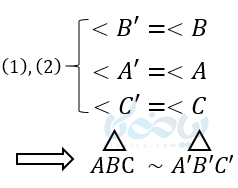
مثال ۳: در شکل زیر دو زاویه \( \LARGE <A = < D \)با هم برابرند\( \LARGE X,Y \) را بدست آورید ؟
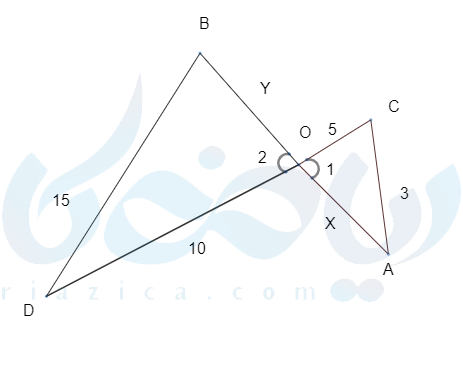
حل ۳: با استفاده از آموزش قضیه تالس و نوشتن قضایای تشابه داریم .
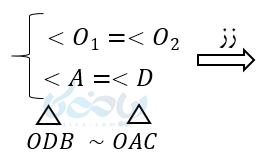

نکته مهم در حل مسٔله های تشابه مثلث ها
گاهی دانش آموزانی در نوشتن ضلعهای متناسب دچار مشکل هستند. به خصوص در بعضی شکلها که اضلاع مشترک دارند. برای تشخیص ضلعهای متناظر متناسب باید ابتدا زاویههای برابر را پیدا کرده. در این حالت اضلاع روبرویشان با هم متناسب هستند.
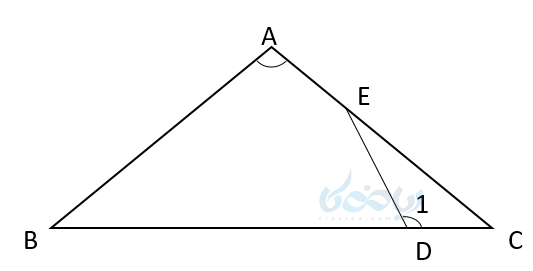
مثلاً در شکل بالا:
\( \LARGE <A = < D_1 \)
مشترک \( \LARGE <C = <C \)
\( \LARGE <E = <B \)
چون زاویه \( \LARGE < D_1 \)در مثلث DEC روبروی EC است و ضلع BC در مثلث ABC روبروی زاویه A است، پس دو ضلع EC و BC باهم متناسب هستند. کسر رو به رو را در نظر داشته باشید: \( \Large \frac{EC}{BC} \)
از طرفی چون زاویه C بین دو مثلث EDC و ABC مشترک است، پس اضلاع رو به روی این زاویه در دو مثلت نیز باهم متناسب هستند. در نتیجه میتوان کسر رو به رو را نیز در نظر گرفت \( \Large \frac{ED}{AB} \)
در نهایت برای اضلاع رو به روی E و B نیز به همین ترتیب کسر \( \Large \frac{DC}{AC} \) را در نظر میگیریم. نتیجه نهایی:
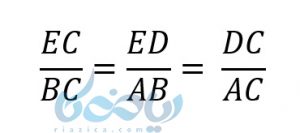
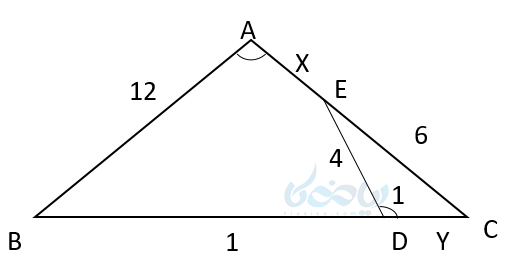
مثال ۴: در شکل زیر \( \LARGE <A = < D_1 \) اندازه اضلاع خواسته شده را بدست آورید ؟
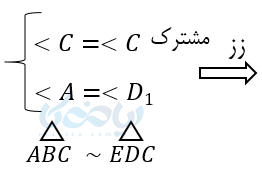
حل ۴: با استفاده از آموزش قضیه تالس و نوشتن قضایای تشابه داریم:
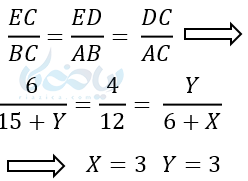
یک مفهوم اساسی در تشابه مثلث ها
وقتی دو مثلث با هم متشابه هستند، تمامی موارد زیر نیز با هم تناسب دارند:
- اضلاع
- ارتفاعها
- نیمسازها
- میانهها
- محیطها
- مساحتهایشان
اگر نسبت اضلاع به یکدیگر \( \Large K \) باشد، نسبت ارتفاعها، نیمسازها، میانه ها و محیط هایشان نیز \( \Large K \) خواهد بود. اما نسبت مساحتهایشان \( \Large K^2 \) میشود.
در ادامه تناسب هر یک از موارد گفته شده را باهم اثبات میکنیم.
قضیه 1: تناسب ارتفاعها
ثابت کنید در دو مثلث متشابه نسبت ارتفاعها به یکدیگر با نسبت اضلاع آنها برابر است.
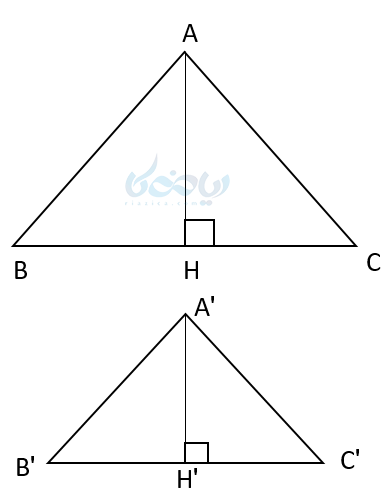
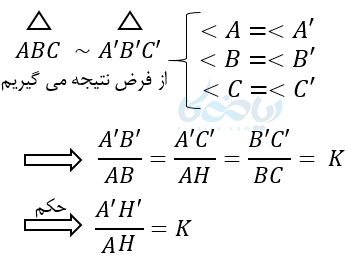
چون دو مثلث ABC و ‘A’B’C متشابه هستند پس نسبت تشابه اضلاع k می باشد .حال ارتفاعهای وارد بر اضلاع BC و ‘B’C را رسم میکنیم. حال دو مثلث ABH و ‘A’B’H را در نظر میگیریم. این دو مثلث طبق اصل تشابه مثلث ها با هم متشابهاند.
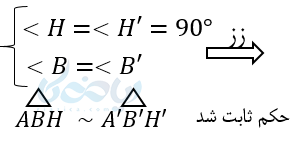
پس از تشابه این دومثلث تناسب اضلاع زیر را نتیجه می گیریم وحکم ثابت می شود.
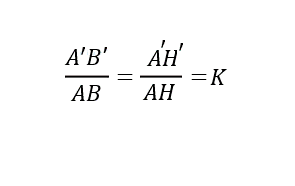
ادامهٔ قضایای مربوط به تشابه مثلث ها
قضیه 2: تناسب میانهها
ثابت کنید در دو مثلث متشابه نسبت میانهها با نسبت تشابه اضلاع با هم برابر است.
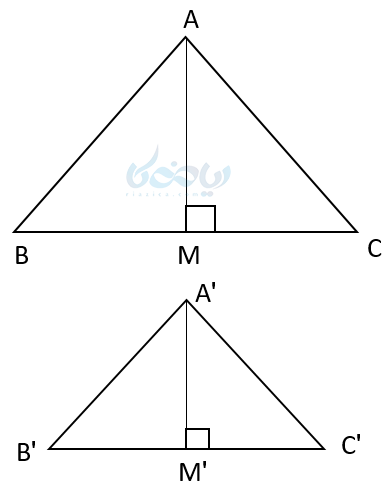
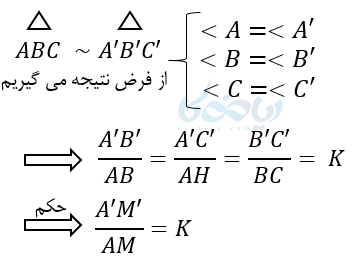
در مثلث ABC و ‘A’B’C میانههای وارد بر BC و ‘B’C را رسم میکنیم. پس:
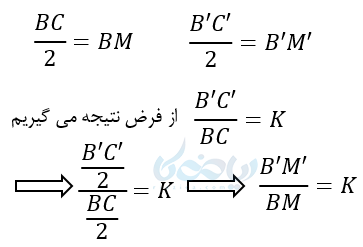
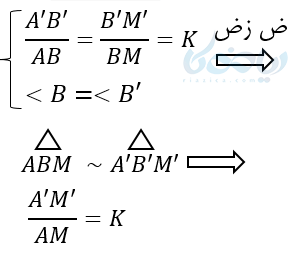
قضیه 3 : تناسب نیمسازها
ثابت کنید در دو مثلث متشابه، نسبت نیمسازها با نسبت اضلاع با هم برابر است.
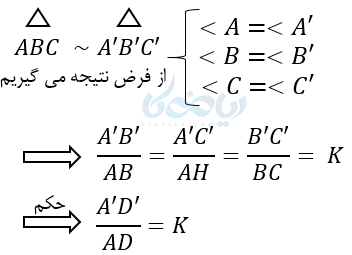
نیمساز دو زاویه A و ‘A را رسم میکنیم و آنها را AD و ‘A’D مینامیم.
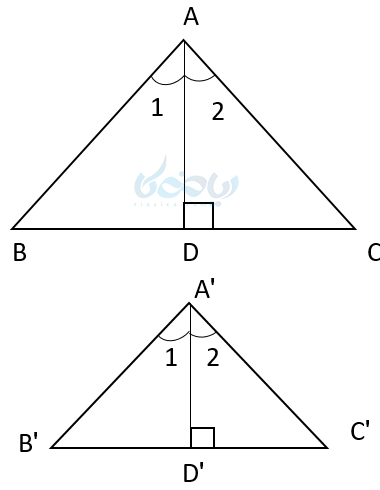
چون A’ = <A> است، پس وقتی نیمسازهای آنها را رسم میکنیم زوایای \( \LARGE <A’_1 = < A \) نیز با هم برابر میشوند. پس داریم:
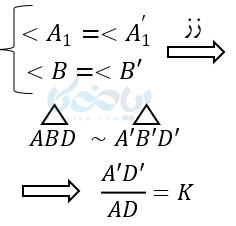
اثبات دو قضیه زیر را به عهده شما میگذاریم.
قضیه 4: تناسب محیطها
ثابت کنید در دو مثلث متشابه، نسبت محیطها با نسبت اضلاع متناسب برابر است.
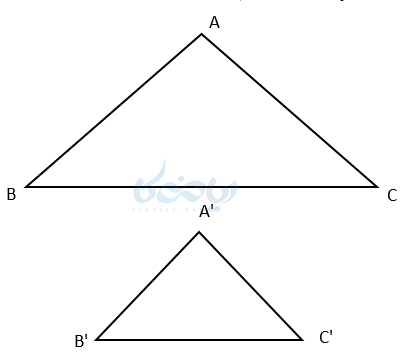
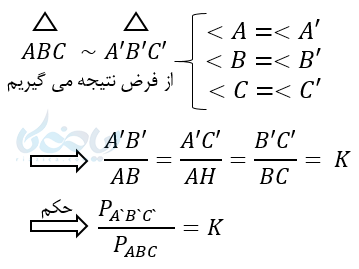
نکته: رابطهٔ زیر یکی از خواص تناسب است:
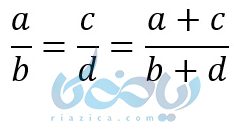
از این نکته برای اثبات قضیه استفاده کنید.
قضیه 5: تناسب مساحتها
ثابت کنید در دو مثلث متشابه، نسبت مساحتها با مجذور نسبت اضلاع متناسب برابر است.

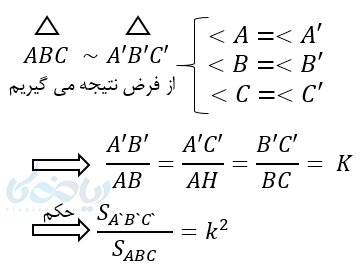
چند مثال از قضایایی که تا کنون یادگرفتم
مثال ۵: دو مثلث با هم متشابهاند. اگر نسبت تشابه آنها \( \Large \frac{3}{5} \) باشد، نسبت مساحتهای آنها چقدر است؟
حل ۵: در قضیه تالس یاد گرفتیم که در دو مثلث متشابه، نسبت مساحتها با مجذور نسبت اضلاع متناسب برابر است. در نتیجه مینویسیم:
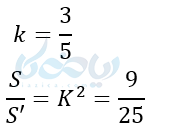
مثال ۶: دو مثلث ABC و ‘A’B’C با هم متشابهاند. اگر محیط ABC برابر 10 و AB’ = 8 و B’C’ = 7 و A’C’ = 5 باشند، سوالات زیر را پاسخ دهید:
الف ) نسبت مساحتهای آنها چقدر است؟
ب ) اگر مساحت ABC = 18 باشد مساحت ‘A’B’C چقدر است ؟
حل ۶: در آموزش قضیه تالس یاد گرفتیم که در دو مثلث متشابه نسبت محیط ها با نسبت اضلاع متناسب با هم برابر است و نسبت مساحت ها با مجذور نسبت اضلاع.
الف)
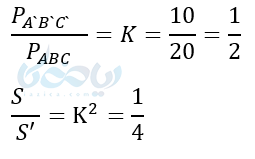
ب)

مثال ۷: اگر دو مثلث متشابه باشند و نسبت ارتفاع های آنها \( \Large \frac{3}{7} \) باشد و یک ضلع مثلث کوچکتر ۵ باشد متناظر آن در مثلث بزرگتر چقدر است ؟
حل ۷: در آموزش قضیه تالس یاد گرفتیم که در دو مثلث متشابه نسبت ارتفاع ها به یکدیگر با نسبت اضلاع آنها برابر است.
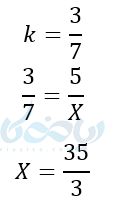
مثال ۸: اضلاع مثلث ABC و 9 , 12 , 15 میباشند و با مثلث ‘A’B’C متشابه است. اگر مساحت ‘A’B’C برابر 81 باشد، نسبت محیطهای آنها چقدر است ؟
حل ۸: مثلث ABC قائم الزاویه است زیرا داریم:
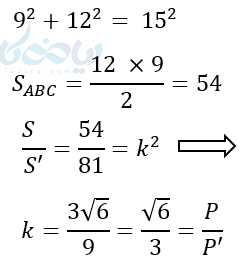
چند نکته مهم در مورد تشابه مثلث ها
- هر دو مثلث متساوی الاضلاع با هم متشابه هستند.
- هر دومثلث متساوی الساقین با زاویه رأس برابر متشابهند.
- هر دومثلث متساوی الساقین با دو زاویه زیر ساق برابر با هم متشابهند.
- هر دو مثلث قائم الزاویه با یک زاویه تند برابر با هم متشابهند.
قبل از خواندن این پست درسنامه آموزش قضیه تالس را مطالعه کنید ودر ادامه پست ترسیم های هندسی را بخوانید.
آخر کلاس تشابه مثلث ها
در این نوشتار که از کتاب ریاضی یازدهم تجربی، مفهوم تشابه مثلث ها را با مثالهای متنوع و رسم شکلهای گوناگون باهم یادگرفتیم. همچنین تمامی قضیههای این مفهوم مهم را بررسی و اثبات کردیم.
در صورتیکه که هرگونه سوالی از این مبحث داشتید، میتوانید سوال خود را در بخش دیدگاهها در پایین همین قسمت مطرح کنید. کارشناسان ریاضیکا به سوالات شما پاسخ خواهند داد.





عالیه ممنون ???
سلام ممنون از نظر و انرژی فوق العاده تون.
خیلی عالی بود ممنون
سلام ممنون از نظرتون
خوشحالیم که براتون مفید بود ?
در دو مثلث متشابه کدام یک از موارد زیر برابر نسبت تشابه نمیباشد؟ ۱)نسبت ارتفاع ها ۲)نسبت اضلاع ۳)نسبت محیط ها۴)نسبت مساحت ها ممنون میشم پاسخ بدین.?
سلام و وقت به خیر نسبت مساحت ها برابر با نسبت تشابه به توان دو می باشد.
نسبت مساحت دو مربع 9به 25 می بشد نسبت تشابه انها کدام است
سلام و عرض ادب
نسبت تشابه برابر با جذر مساحت ها می باشد یعنی ۳ به ۵ خواهد بود.
موفق باشید.
اگر دریک مثلث نسبت دوضلع برابر نسبت ارتفاع های نظیر ان دو باشد مثلث چیست؟
با سلام دوست عزیز
مثلث یا متساوی الساقین است یا متساوی الاضلاع
سلام
نسبت مساحتها در دو مثلث متشابه با نسبت تشابه K را ثابت کنید؟
با سلام وقت به خیر
در قضیه پنج همین پست اثبات شده
خیلیی عالییییے
با سلام
ممنون از لطف شما
با سلام
ممنون از لطف شما
سپاس فراوان
با سلام وعرض ادب
خواهش میکنم موفق باشبد
خیلی ممنون مطلب بسیار مفیدی بود
در دو شکل که نسبت تشابه شان x است درباره نسبت تشابه قطر ها چه میتوان گفت؟؟
خیلی طولانی
با سلام وادب
طولانی ولی کامل تا هر کس هر قسمتی که لازم داره بخونه
خیلی مفید بود عالی عالی بود ممنون
با سلام وادب
واقعا خوشحالیم چون برای تهیه این پستها واین سایت زحمت زیادی کشیدهذشده
ممنوناز وقت وانرژی که برای تدوین این پست گذاشتید واقعا عالیست
با سلام دوست عزیز
ممنون از نظر محبت آمیز شما
خیلی خوب
با سلام ممنون از شما
سپاس از مناعت طبعتون که رایگان علمتون رو در اختیار بقیه قرار میدین
عالی عالی
با سلام ممنون از نظر شما