آموزش ریاضی پایه یازدهم تجربی، آموزش هندسه دهم ریاضی

تناسب و خواص تناسب : یک نتیجه از قضیه تالس – یک دنیای متناسب 🎢🔺

آخرین بروزرسانی در تاریخ 1402/10/08 توسط سید ایمان موسوی نطنزی
تناسب و خواص تناسب : یک نتیجه از قضیه تالس - یک دنیای متناسب!
۰۸
فروردین

در کتاب ریاضی پایه یازدهم، فصل دوم و هندسه یک پایه دهم، ما با قضیه تالس و تشابه آشنا می‌شویم. ملاحظه می‌کنید که از تناسب و خواص تناسب استفاده زیادی می‌شود. پس بهتر آن است که ابتدا با تناسب و خواص آن کاملاً آشنا شویم. در نهایت قادر خواهیم بود در قسمت بعد، یعنی قضیه تالس و تشابه، از خواص تناسب بهره ببریم.

تعریف تناسب

رابطه بین دو نسبت را تناسب می گویند واین رابطه از نوع تساوی است وقتی دو نسبت با هم برابر باشند می گوییم با هم تناسب دارند یا به بیان دیگر متناسب هستند پس نسبت رابطه بین دوعدداست وتناسب رابطه بین دو نسبت که این دو مفهوم مفاهیمی کلیدی در ریاضیات وهندسه وسایر علوم می باشند.

خواص تناسب

خواص تناسب عبارتند از:

  1. طرفین وسطین
  2. تبدیل حاصلضرب به تناسب
  3. تعویض جای طرفین با وسطین
  4. معکوس کردن تناسب
  5. ترکیب نسبت در صورت یا مخرج
  6. تفاضل نسبت در صورت یا مخرج
خرید پکیج دوره محاسبات سریع 💎🔮

قیمت اصلی 799.000 تومان بود.قیمت فعلی 397.000 تومان است.افزودن به سبد خرید

1– طرفین وسطین

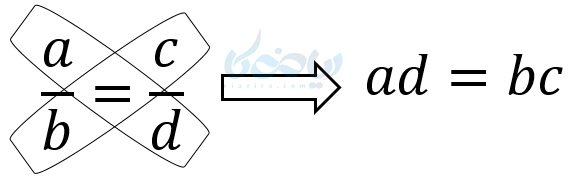
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها طرفین وسطین است.

اثبات:

طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها طرفین وسطین است.

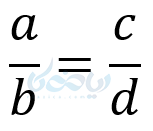
اگر هر دو صورت را در  \( \LARGE bd  \) ضرب کنیم داریم:

طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها طرفین وسطین است.

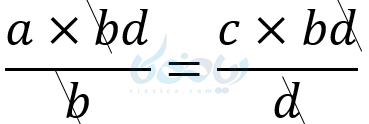
و در نتیجه داریم:

طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها طرفین وسطین است.

2– تبدیل حاصل ضرب به تناسب

هر حاصل ضرب را می توان به یک تناسب تقسیم کرد.

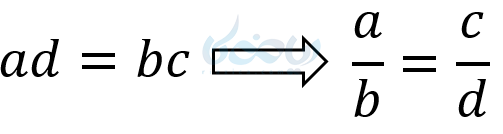
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تبدیل حاصل ضرب به تناسب است.

اثبات:

طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تبدیل حاصل ضرب به تناسب است.

طرفین را به \( \LARGE db \) تقسیم می‌کنیم:

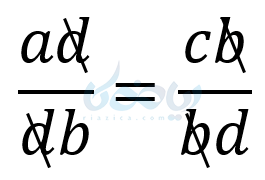
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تبدیل حاصل ضرب به تناسب است.

و در نتیجه داریم:

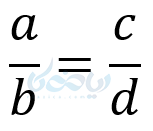
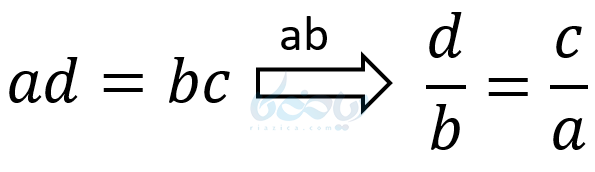
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تبدیل حاصل ضرب به تناسب است.

نکته ۱: می توان طرفین را به  \( \LARGE ab \) یا  \( \LARGE cd \) یا \( \LARGE ac \)  تقسیم کرد، در این صورت تناسب‌های زیر بدست می آید.

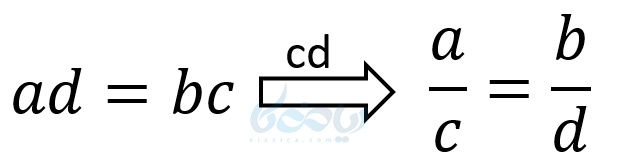
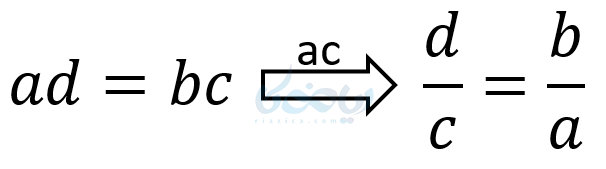
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تبدیل حاصل ضرب به تناسب است.

طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تبدیل حاصل ضرب به تناسب است.

طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تبدیل حاصل ضرب به تناسب است.

پس می توان هر حاصل ضرب را با توجه به مسئله مورد نظر به 4 نوع تناسب تبدیل کرد.

3– تعویض جای طرفین با وسطین

در هر تناسب می توان جای طرفین را با هم یا جای وسطین با هم عوض کرد، تناسب بدست آمده یک تناسب درست است.

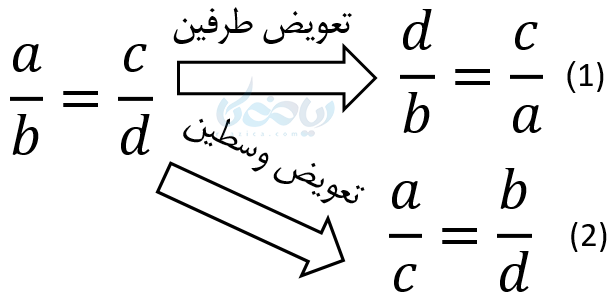
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تعویض جای طرفین با وسطین است.

اثبات 1:

طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تبدیل حاصل ضرب به تناسب است.

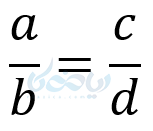
طرفین را در  \( \LARGE bd  \) ضرب می‌کنیم و داریم:

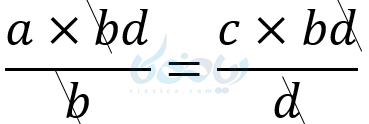
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تعویض جای طرفین با وسطین است.

به این ترتیب داریم:

طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها طرفین وسطین است.

و در نهایت، طرفین را به  \( \LARGE ab \) تقسیم می‌کنیم و خواهیم داشت:

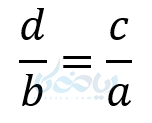
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تعویض جای طرفین با وسطین است.

اثبات 2:

طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تبدیل حاصل ضرب به تناسب است.

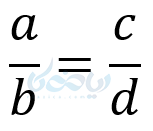
طرفین را در  \( \LARGE bd  \) ضرب می‌کنیم و داریم:

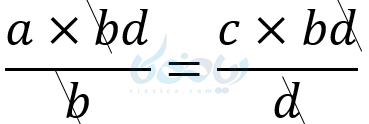
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تعویض جای طرفین با وسطین است.

به این ترتیب داریم:

طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها طرفین وسطین است.

در نهایت طرفین را به  \( \LARGE dc \) تقسیم می‌کنیم و در نتیجه خواهیم داشت:

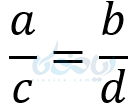
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تعویض جای طرفین با وسطین است.

4– معکوس کردن تناسب

طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها معکوس کردن تناسب است.

اثبات :


طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تبدیل حاصل ضرب به تناسب است.

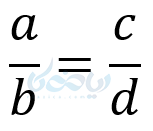
طرفین را در  \( \LARGE bd  \) ضرب می‌کنیم و داریم:

طرفین را به  \( \LARGE ac \) تقسیم می‌کنیم:

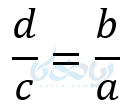
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها معکوس کردن تناسب است.

جای طرف اول و دوم را برعکس کنید:

طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها معکوس کردن تناسب است.

خرید پکیج دوره محاسبات سریع 💎🔮

قیمت اصلی 799.000 تومان بود.قیمت فعلی 397.000 تومان است.افزودن به سبد خرید

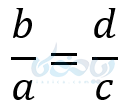
5– ترکیب نسبت در صورت یا مخرج

الف ) ترکیب نسبت در صورت

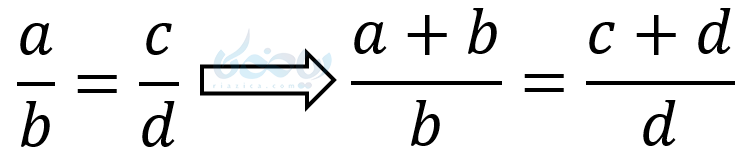
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها ترکیب نسبت در صورت یا مخرج است.

اثبات: کافی است، طرفین را بعلاوه یک کنیم.

طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تبدیل حاصل ضرب به تناسب است.

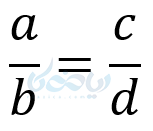
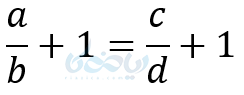
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها ترکیب نسبت در صورت یا مخرج است.

و در نتیجه خواهیم داشت:

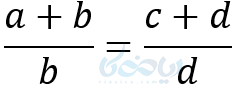
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها ترکیب نسبت در صورت یا مخرج است.

ب ) ترکیب نسبت در مخرج

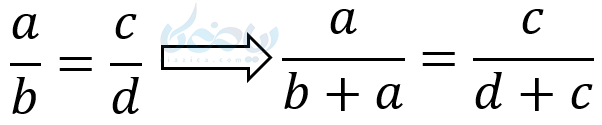
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها ترکیب نسبت در صورت یا مخرج است.

اثبات:

 

ترکیب نسبت در صورت یا مخرج.

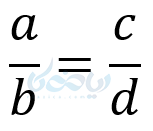
معکوس کردن:

ترکیب نسبت در صورت یا مخرج.

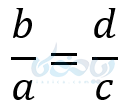
طرفین را بعلاوه یک می‌کنیم:

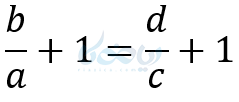
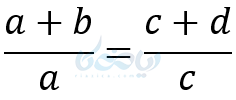
ترکیب نسبت در صورت یا مخرج.

ترکیب نسبت در صورت یا مخرج.

معکوس کردن تناسب:

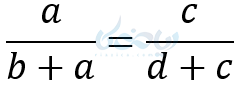
ترکیب نسبت در صورت یا مخرج.

 

6– تفاضل نسبت در صورت یا مخرج

الف ) تفاضل نسبت در صورت

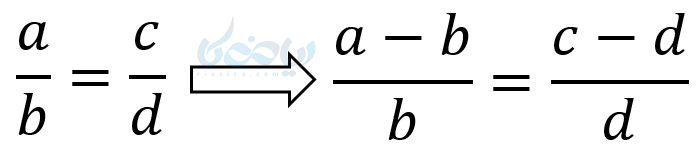
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تفاضل نسبت در صورت یا مخرج است.

اثبات:

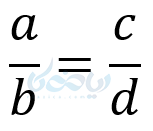
تفاضل نسبت در صورت یا مخرج.

طرفین را منهای یک می‌کنیم:

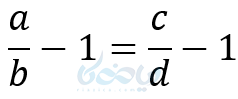
تفاضل نسبت در صورت یا مخرج.

و در نتیجه خواهیم داشت:

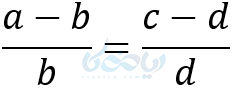
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تفاضل نسبت در صورت یا مخرج است.

ب ) تفاضل نسبت در مخرج

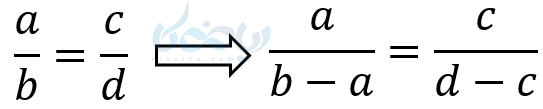
طبق قضیه تالس ما به خواص تناسب میرسیم که یکی از آن ها تفاضل نسبت در صورت یا مخرج است.

اثبات:

 

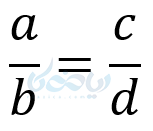
تفاضل نسبت در صورت یا مخرج.

معکوس کردن:

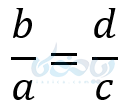
تفاضل نسبت در صورت یا مخرج.

طرفین را منهای یک می‌کنیم:

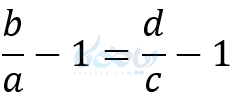
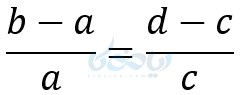
تفاضل نسبت در صورت یا مخرج.

تفاضل نسبت در صورت یا مخرج.

معکوس کردن تناسب:

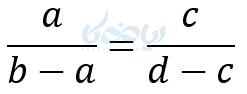
تفاضل نسبت در صورت یا مخرج.

حتما در ادامه پست قضیه تالس و تشابه مثلث ها را مطالعه کنید.

ویدیو از تناسب وخواص تناسب

در این ویدیو نتایج نسبت وتناسب که در کتاب هندسه دهم ریاضی آورده شده برای شما آموزش داده شده است

آخر کلاس تناسب و خواص تناسب

قشنگ‌ترین نکته مبحث تناسب و خواص تناسب برای من، پی‌بردن به خلقت بی‌نقص خداوند است. خدایی که هر مخلوقی را در این دنیا براساس قواعدی معین آفریده. به شکلی که هر چیزی در این دنیا با محیط پیرامون خود و حتی با خودش در تناسب است.

شما عزیزان به کمک بحث تناسب و خواص تناسب می‌توانید در بخش های، تشابه، تالس و روابط طولی مثلثاتی از آن‌ها استفاده کنید. ما سعی‌مان بر آن بوده همه مفاهیم و آموزش ها را در برگیریم و هیچ جای ابهامی برای شما نگذاریم.

هر گونه سوال و یا نظرتان از این نوشتار آموزشی را با ما در قسمت نظرات مطرح کنید. گروه آموزشی ریاضیکا به سوالات شما عزیزان به سرعت پاسخ خواهد داد.

خرید پکیج دوره محاسبات سریع 💎🔮

قیمت اصلی 799.000 تومان بود.قیمت فعلی 397.000 تومان است.افزودن به سبد خرید

سید ایمان موسوی نطنزی

20 دیدگاه برای “تناسب و خواص تناسب : یک نتیجه از قضیه تالس – یک دنیای متناسب 🎢🔺 ”

  1. neda گفته:

    عالیه?
    ممنون بابت زحماتتون
    ایکاش ویدیو هم تو سایتتون داشتید
    ولی با این حال سایتتون فوق العاده اس

    پاسخ
    • سید ایمان موسوی نطنزی گفته:

      سلام دوست عزیر
      خیلی خوشحال شدیم که براتون مفید واقع شده بود.
      حتما در آپدیت های بعدی ویدیو رو قرار می‌دهیم.

      پاسخ
  3. محمد مهدی گفته:

    سلام در اثبات ویژگی چهارم نوشتید تقسیم بر ac می کنیم آیا دلیلی بر مخالف صفر بودن آن وجود دارد

    پاسخ
    • سید ایمان موسوی نطنزی گفته:

      سلام و عرض ادب
      همیشه در تقسیم بر یک عبارت جبری شرط مخالف صفر بودن آن در آن مستتر است، چون مخرج صفر بی معنی است.
      موفق باشید.

      پاسخ
  4. علی گفته:

    فک نکنم با این آموزشتون، توی مرحله های مسائل مثلثات هنگ کنم?
    خیلی مفید بود. مرسی از شما.

    پاسخ
    • سید ایمان موسوی نطنزی گفته:

      سلام و عرض ادب
      ممنون از انرژی و پیام پرمهرتون و خوشحالیم از اینکه براتون مفید واقع شده.
      موفق باشید.

      پاسخ
    • سید ایمان موسوی نطنزی گفته:

      سلام عرض ادب
      ممنون از دیدگاه مثبت و نگاه مهرآمیزتون.
      موفق باشید.

      پاسخ
    • دبیر ارشد ریاضیکا گفته:

      با سلام وادب
      دوست عزیز با دقت بخونید اثباتش هست

      پاسخ
  9. یک دوست گفته:

    با تشکر از زحماتتون . همه ی حالات رو به خوبی گفتین ولی
    اگه ترکیب قسمت 5 و 6 رو هم اضافه میکردین ، کامل کامل میشد.
    (c+d)/(c-d) = (a+b)/(a-b)

    پاسخ
  12. ستایش گفته:

    عالی بود فقط استاد از کجا بفهمیم کیا از اینا استفاده کنیم؟

    پاسخ

دیدگاهتان را بنویسید

نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند *