آموزش هندسه دهم ریاضی، آموزش ریاضی پایه یازدهم تجربی
آموزش قضیه تالس 🎢✏️ – قدم به قدم با تصویر
آموزش قضیه تالس در مورد دو خط موازی است که یکی از قضایای مهم در هندسه میباشد. این قضیه موارد استفاده زیادی در پیدا کردن اندازه اضلاع مثلث در شکلهای دیگر دارد. تالس در حدود 60 سال قبل از میلاد مسیح زندگی میزیسته و این مفهوم را بیان کرده است. در کتاب ریاضی پایه یازدهم تجربی در فصل دوم به قضیه تالس و نتایج آن پرداخته شده است. ما در ریاضیکا اثبات صورت این قضیه و نتایج و تعمیم آنرا به زبان ساده درادامه برای شما بیان کردهایم.
صورت قضیه تالس
اگر خط موازی یکی از اضلاع مثلث رسم شود و دو ضلع دیگر را قطع کند، روی آنها پارهخطهای متناسب به وجود میآورد.
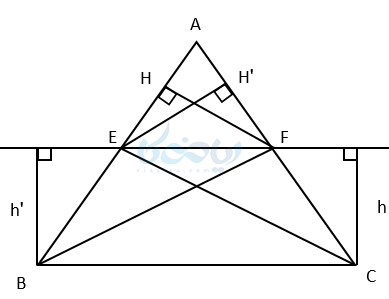

اثبات قضیه تالس
برای اثبات این قضیه ابتدا از نقطه F به B و از نقطه E به C وصل میکنیم. دو مثلث EFC و EFB را در نظر میگیریم حال ارتفاع ضلع مشترک EF را در دو مثلث رسم میکنیم. آنها را \( \Large h \) و \( \Large h’ \) مینامیم. چون EF موازی با BC میباشد و با توجه به اینکه \( \Large h \) و \( \Large h’ \) بین دو خط موازی واقع هستند، پس با هم برابرند. بنابراین مساحت دو مثلث تشکیل شده با هم برابر است. یعنی داریم:
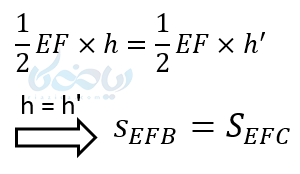
حال مثلث AEF را در نظر میگیریم. دو ارتفاع وارد بر AF و AE را رسم میکنیم. یعنی ‘EH و EH’ .FH در مثلث AFE بر AF عمود شده و در مثلث EFC بر امتداد FC عمود شده. همچنین FH بر AE در مثلث AEF عمود شد و در مثلث EFB بر امتداد EB عمود شده است.
حال تناسب درست زیر را تشکیل میدهیم. در این تناسب صورتها با هم و مخرجها با هم برابرند.
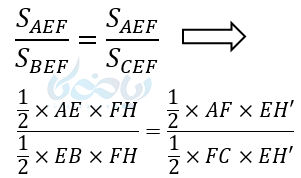
حال با ساده کردن این تناسب حکم ثابت میشود و داریم:
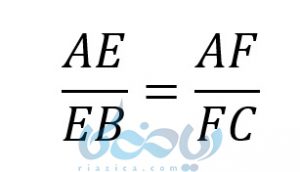
نتیجه اول از قضیه تالس
در قضیه تالس به تناسب زیر رسیدیم. حال اگر این تناسب را ترکیب نسبت در صورت کنیم خواهیم داشت:
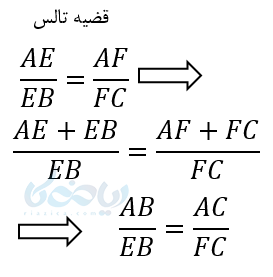
به تناسبی که در این قضیه داریم تناسب جزء به جزء میگویند. به نتیجه به دست آمده در بالا نیز تناسب کل به جزء گفته میشود.
نتیجه دوم
حال اگر قضیه تالس را ترکیب نسبت در مخرج کنیم خواهیم داشت:

اگر قضیه تالس و نتایج آن را معکوس کنیم باز هم این نتایج برقرار است . یعنی وقتی در یک مثلث ضلعی موازی یکی از اضلاع مثلث رسم شود، پاره خط های ایجاد شده به صورت:
- جزء به جزء و برعکس
- جزء به کل و کل به جزء و معکوسشان
برقرار هستند. قضیه تالس به ما هر کدام از این موارد را میآموزد.
آموزش تعمیم قضیه تالس
مثلث ABC را در نظر بگیرید که درآن EF با BC موازی باشد. طبق نتیجه قضیه تالس داریم:
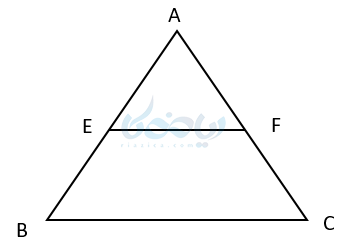
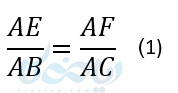
حال در همین مثلث از نقطه F خط FN را موازی ضلع AB در نظر میگیریم. طبق نتیجه قضیه تالس خواهیم داشت:
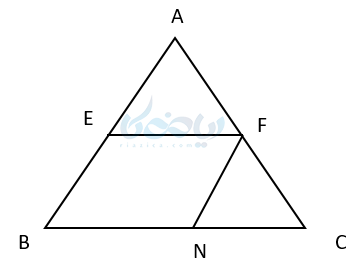
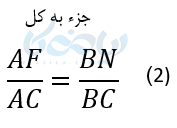
اگر چهار ضلعی EFNB را ملاحظه کنید متوجه خواهید شد که یک متوازی الاضلاع تشکیل شده است. چون اضلاع رو به روی آن دو به دو با هم موازی هستند. همانطور که میدانیم ضلعهای رو به رو در متوازی الاضلاع با هم برابر هستند بنابراین: EF = BN .
حال از مقایسهٔ شکلهای 1 و 2 نتیجه میگیریم:
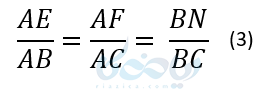
حال اگر به جای BN ضلع مساویش یعنی EF را در رابطهٔ 3 جایگذاری کنیم خواهیم داشت:
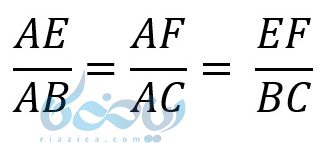
به زبان دیگر میتوان گفت وقتی ضلعی موازی یکی از اضلاع مثلث رسم شود، یک مثلث کوچک تشکیل میشود. پس در شکل بالا ضلعهای مثلث AEF با ضلعهای مثلث اصلی یعنی ABC متناسب است.
یکی دیگر از کاربردهای قضیه تالس
یکی از کاربردهای قضیه تالس و نتایج و تقسیم آن پیدا کردن اضلاع مثلثی است که بعضی از اضلاع آن مجهول است. در زیر چند مثال از این قضیه را برایتان آوردهایم تا با کاربردهای آن بیشتر آشنا شوید.
مثال ۱: در شکل زیر MN با BC موازی است مقدار \( \Large x \) و \( \Large y \) بدست آورید ؟
حل ۱: با استفاده از آموزش قضیه تالس و نوشتن نسبت ها داریم .
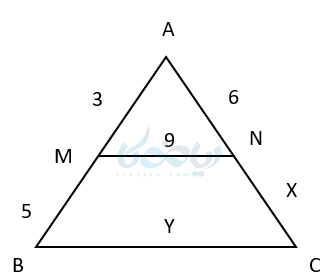
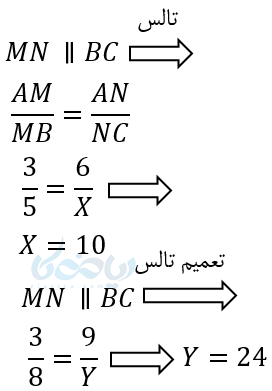
دقت کنید در مثلث بالا برای بدست آوردن X هم از تناسب جزء به جزء هم از تناسب جزء به کل می توان استفاده کرد . ولی برای بدست آوردن Y طبق تعمیم تالس فقط از تناسب جزء به کل باید استفاده کرد .
مثال ۲: در شکل زیر MN با BC موازی است مقدار \( \Large x \) بدست آورید ؟
حل ۲: با استفاده از آموزش قضیه تالس و نوشتن نسبتها داریم.
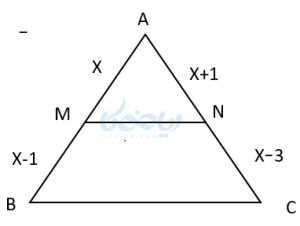
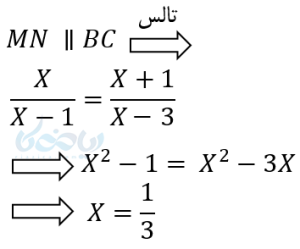
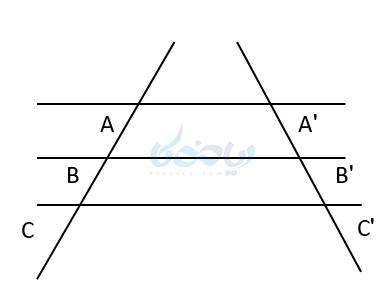
نکته: این قضیه در مورد خطهای موازی دیگر نیز برقرار است و به صورت زیر بیان میشود.
هرگاه چند خط موازی با استفاده از دو خط مورب قطع شوند نسبتهای ایجاد شده روی آنها با هم برابرند.
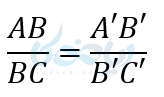
انواع استدلال:
در علم ریاضیات و حتی سایر علوم تمامی مسائل با استفاده از دو استدلال کلی اثبات میرسند که در ادامه به توضیح و بررسی هرکدام میپردازیم:
- استدلال استقرایی
- استدلال استنتاجی
استدلال استقرایی
به نتایجی که از طریق مشاهده، اندازهگیری، آزمایش، حدس و گمان و تجربه دست میآیند، استدلال استقرایی گفته میشود. مثلاً با اندازهگیری زوایای مثلث به این نتیجه میرسیم که مجموع زوایای مثلث همیشه ۱۸۰ درجه خواهد شد. این نوع استدلال با اینکه ارزشمند است اما خیلی قابل استفاده نیست. چون انسان و وسایل اندازهگیری دارای خطا هستند. نوع دیگر استدلال که قابل استفاده و محکم و متقن است استدلال استنتاجی میباشد.
استدلال استنتاجی
در استدلال استنتاجی نتایج با استفاده از واقعیت و اصول ریاضی که درستی آنها را قبلاً پذیرفتهایم به دست میآیند. بعنوان یک مثال مهم اثبات قضیه تالس را با استفاده از همین استدلال انجام دادیم.
دو مفهوم مهم در ریاضیات برای اثبات عکس قضیه تالس
برای اثبات عکس قضیه تالس نیاز است که با دو مفهوم خیلی مهم آشنا شویم. این دو مفهوم مهم که در اثبات قضایا و موارد مختلف دیگر بسیار کاربرد دارد عبارتند از:
- برهان خلف
- تعریف عکس یک قضیه
در ادامه به بررسی این دو مفهوم میپردازیم:
برهان خلف
یکی از روشهای اثبات قضایا برهان خلف است. در روش برهان خلف به جای روش مستقیم، یعنی به جای اینکه از فرض به حکم برسیم، فرض میکنیم حکم نادرست باشد (فرض خلف). سپس به تناقض میرسیم و نتیجه میگیریم فرض خلف باطل است.
عکس یک قضیه
اگر در یک قضیه جای فرض و حکم عوض شود به نتیجه به دست آمده عکس قضیه گفته میشود. عکس یک قضیه لزوماً همیشه درست نیست. حال میخواهیم عکس قضیه تالس به روش برهان خلف برایتان اثبات کنیم.
اثبات عکس قضیه تالس به روش برهان خلف
اگر در مثلثی ضلعی دو ضلع مثلث را قطع کند و روی آنها پارهخطهای متناسب وجود آورد، حتماً آن خط با ضلع سوم موازی است.
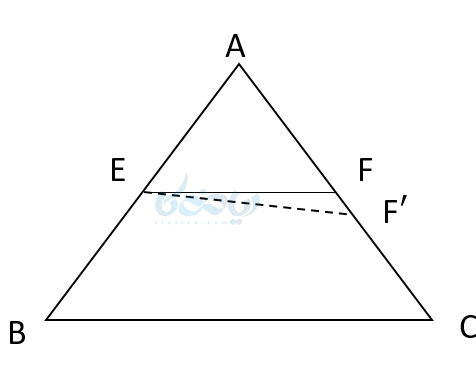
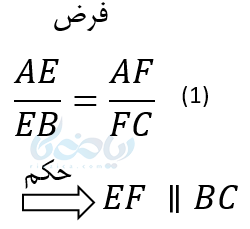
فرض خلف:
فرض میکنیم EF با BC موازی نباشد. از نقطه E خطی مانند ‘EF میتوان رسم کرد که با BC موازی باشد. پس داریم :
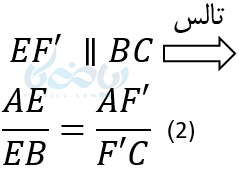
از مقایسه رابطه 2 با فرض نتیجه میگیریم:
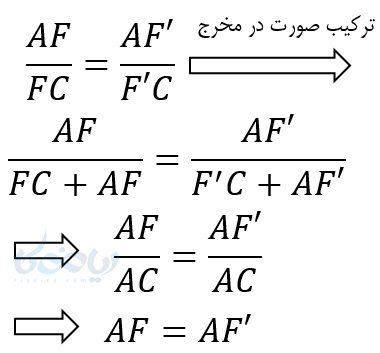
از تساوی AF و ‘AF نتیجه میشود نقطه F و ‘F بر هم منطبق می باشند . پس فرض خلف باطل است . EF موازی BC حکم ثابت شد.
در ادامه توصیه میشه پست ارزشمند تشابه مثلث ها واثبات بوسیله قضیه تالس را بخوانید.
ویدیو از آموزش قضیه تالس
در این ویدیو آموزش قضیه تالس وعکس آن وتعمیم آن طبق کتاب هندسه دهم ریاضی آورده شده است
آخر کلاس قضیه تالس
دوستان عزیز من امروز با هم قضیه تالس کامل یاد گرفتیم (ترکوندیم 🙂 ) . تشابه مثلث ها و اثبات بوسیله قضیه تالس ? و تناسب و خواص تناسب : یک نتیجه از قضیه تالس ? ادامه این مبحث هست برا اینکه خستهتون نکنم جداشون کردم. بچهها اینا رو هم حتما بخونید.
رفقا سوالاتتون زیر همین پست برامون کامنت کنید. قطعا بچههای ریاضیکا بهتون جواب میدم.





عالییییی بود
سلام وعرض ادب
ممنون از لطف شما وخوشحالیم که براتون مفید بوده
خیلی عالیییی
دمتون گرم
فقط یه سوال
به جز برهان خلف روشی برای اثبات عکس قضیه تالس نیست؟!
اگر هست ممنون میشم راهنمایی ام کنین
با سلام برای اثبات هر قضییه راههای متعددی هست مثلا برای اثبات قضیه فیثاغورس تا به حال ۱۸۰ اثبات پیدا شده در مورد عکس تالس ساده ترین روش که در کتاب یازدهم آمده برهان خلف است میتوانید به عنوان یک کار تحقیقی شما روش دیگری بیابید وبرای ما هم بفرستید تا با نام خودتان در سایت نوشته شود
یج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
از کجا بفهمیم از تالس بریم یا تعمیم تالس؟
با سلام دوست عزیز
با توجه به چیزی که صورت مسئله خواسته باید متوجه بشی
سلام عالی بود
فقط یه سوال چرا اون اول اثبات دوتا مثلث(EFC،EFB) را آوردید؟؟
با سلام وعرض ادب
اول ثابت کردیم مساحت این دو مثلث با هم برابر هست تا در قسمت دوم بتونیم یک تناسب درست بنویسیم اگه برابر نباشند اون تناسبی که نوشتیم رو نمیتونستیم نتیجه بگیریم
اثبات ویدیویی این قضیه در فروشگاه سایت هست میتونید استفاده کنید و بهتر متوجه بشید
برای بهتر فهمیدن قضایای هندسه چند بار خودتون قضایا رو برای خودتون اثبات کنید
سلام،ببخشید چگونه امکان بدست اوردن اون ضلع میان خط رو داریم؟(برای مثال توی این سوال mn)
با سلام با تناسب جز به کل در مثالهای پست دقت کنید به جواب میرسید
تعمیم عکس قضیه تالس چه فرقی با تعمیم قضیه تالس داره؟
ببخشید اشکال پروانه ای رو چطور بدست بیاریم؟
منتظر جواب هستم
با سلام وادب
ابتدا زاویه های مساوی رو پیدا کنید اضلاع روبروی آنها با هم متناسب میشوند نسبت آنها رو بنویسید ومجهول رو پیدا کنید
سلام ، در قضیه تالس معمولا جزء بالا به پایین داریم ، خواستم بدونم ایا نسبت جزء پایین به بالا هم هست ؟ اگر هست به چه شکله ؟ یعنی دقیقا برعکس حالت بالا به پایین میشه ؟
باتشکر
با سلام واحترام
بله نسبت رو از هرطرف میشه محاسبه کرد
خیلی عالی واقعا ممنون
سلام عالی فقط جواب مثال منفی یک سوم میشه نه یک سوم مثبت.
سلام دوست عزیز تصحیح شد
منم هر کاری کردم منفی اوردم میشه بیزحمت توضیح بدین؟
سلام دوست عزیز صورت سوال مشکل داشت تصحیح شد
خیلی خوب بود ممنون
با سلام وادب
ممنون از نگاه شما
سلام واقعا عااالی بود ایول بهتون
سلام دوست عزیز
ممنون از لطف وانرژی که به ما دادید
سلام
قضیه تالس رو میشه از تشابه دو مثلث هم اثبات کرد؟
سلام برای اثبات قضیه تالس از تشابه دو مثلث هم می توان استفاده کرد؟
با سلام وادب
خیر چون خود قضایای تشابه از روی تالس اثبات میشه
سلام . ممنون از زحماتتون خوب توضیح دادین . ولی یک سوال داشتم که چطور میتونم قضیه تالس رو کامل یاد بگیرم چون من الان کلاس هشتم رو تموم کردم و این به پایه ام مربوط نیست خودم میخوام این مبحث از هندسه رو کامل مسلط باشم الان دارم روش کار میکنم ولی شما میتونین به من کمک کنین؟
با سلام
هم آمورشی که اینجا گذاشتیم رو میتونید مطاله کنید هم کتاب هندسه یک دبیرستان رو گیر بیارید وبخونید
سلام و تشکر فراوان از شما بسیار عالی بود
با سلام
ممنون از نگاه شما