آموزش ریاضی پایه نهم
مجموعه ها و احتمال ریاضی نهم 🔃🅰️ – قدم به قدم با مثال!
در مبحث مجموعه ها و احتمال ریاضی نهم میخواهیم از دانستههایمان در مورد مجموعه ها برای تعریف دقیق تر فضای نمونه، پیشامد و احتمال، استفاده کنیم. مبحث پیش رو بسیار ساده، کوتاه و جذاب است. مثالهای متنوعی نیز با هم حل خواهیم کرد تا به مبحث مسلط شوید.
تعریف پیشامد با استفاده از مجموعه ها
در درسنامه آموزش احتمال هشتم دیدیم به زبان ساده، پیشامد یعنی اتفاق. مثلاً زمانی که یک تاس را پرتاب میکنیم، پیشامد (اتفاق)های ممکن، رو شدن یکی از اعداد 1 تا 6 است. بنابراین به زبان مجموعه ها، فضای نمونه، مجموعۀ همۀ پیشامدهاست. هر پیشامد نیز، یک زیرمجموعه از فضای نمونه است. در قمست بعد، احتمال رخداد یک پیشامد را در مبحث مجموعه ها و احتمال ریاضی نهم بررسی میکنیم.
تعریف احتمال با استفاده از مجموعه ها
در پایۀ هشتم، محاسبۀ احتمال رخ دادن یک پیشامد را آموختهاید. احتمال رخ دادن یک پیشامد برابر است با تعداد حالتهای مطلوب تقسیم بر تعداد حالتهای ممکن. اگر فضای نمونه را با \(\Large S\) و پیشامد مطلوب را با \(\Large A\) نشان دهیم، احتمال رخ دادن یک پیشامد را میتوان به صورت زیر نشان داد:
\(\LARGE P(A)=\frac{n(A)}{n(S)}\)
یعنی احتمال رخ دادن پیشامد \(\Large A\) برابر است با تعداد اعضای مجموعۀ \(\Large A\) تقسیم بر تعداد اعضای مجموعۀ \(\Large S\). به مثال بعدی از مبحث مجموعه ها و احتمال ریاضی نهم دقت کنید.
مثال تاس
مثال 1: تاسی را میاندازیم. احتمال اینکه عدد زوج بیاید چه قدر است؟
حل: اگر مجموعۀ همۀ حالتها را با \(\Large S\) و مجموعۀ حالتهای مطلوب را با \(\Large A\) نشان دهیم، \(\Large S\) و \(\Large A\) برابرند با:
\(\LARGE S=\{1, 2, 3, 4, 5, 6\}\)
\(\LARGE A=\{2, 4, 6\}\)
مجموعۀ \(\Large S\) همان فضای نمونه و زیرمجموعۀ \(\Large A\) همان پیشامد مطلوب است. میتوانیم \(\Large S\) و \(\Large A\) را با استفاده از نمودار وِن نیز به صورت زیر نمایش دهیم:
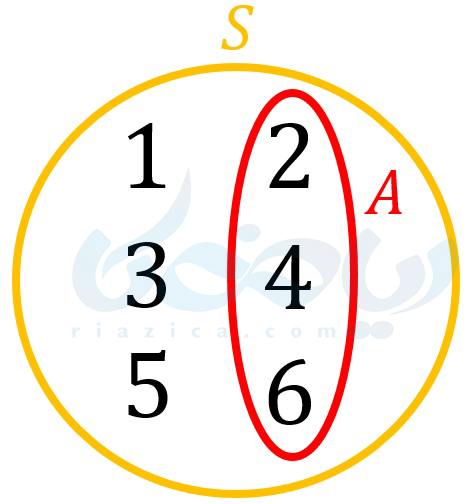
پس، تعداد اعضای مجموعۀ \(\Large A\) برابر با 3 و تعداد اعضای مجموعۀ \(\Large A\) برابر با 6 است. بنابراین، احتمال اینکه عدد زوج بیاید برابر است با:
\(\LARGE P(A)=\frac{n(A)}{n(S)}=\frac{3}{6}=\frac{1}{2}\)
حال، به مثال بعدی از مبحث مجموعه ها و احتمال ریاضی نهم دقت کنید.
مثال خارج کردن مهره از جعبه در مجموعه ها و احتمال ریاضی نهم
مثال 2: در جعبهای 2 مهرۀ قرمز، 4 مهرۀ سفید و 3 مهرۀ سبز داریم. اگر یک مهره را به تصادف از جعبه خارج کنیم، احتمال اینکه این مهره، قرمز یا سبز باشد چه قدر است؟
حل: اگر تعداد حالات مطلوب را با \(\Large n(A)\) نشان دهیم، \(\Large n(A)\) برابر است با مجموع تعداد مهرههای قرمز و سبز. بنابراین، \(\Large n(A)=5\) است. تعداد کل حالات نیز برابر با تعداد کل مهرههاست. پس، \(\Large n(S)=9\) است. بنابراین، احتمال اینکه مهرۀ خارج شده، قرمز یا سبز باشد برابر است با:
\(\LARGE P(A)=\frac{n(A)}{n(S)}=\frac{5}{9}\)
به مثال بعدی از مبحث مجموعه ها و احتمال ریاضی نهم دقت کنید.
مثال پرتاب متوالی تاس در مجموعه ها و احتمال ریاضی نهم
مثال 3: اگر تاسی را دو بار پرتاب کنیم، احتمال اینکه هر دوبار مضرب 3 بیاید چه قدر است؟
حل: میتوانیم حالات مختلف را به صورت زوج مرتب نشان داده که مولفۀ اول آن، نتیجۀ پرتاب اول و مولفۀ دوم آن، نتیجۀ پرتاب دوم باشد. در این صورت اگر حالات مطلوب را با \(\Large A\) نشان دهیم، خواهیم داشت:
\(A=\{(3, 3),(3, 6),(6, 3),(6, 6)\}\)
بنابراین \(\Large n(A)=4\) است. از طرفی تعداد کل حالات برابر با 36 است. زیرا 6 حالت برای پرتاب اول و 6 حالت نیز برای پرتاب دوم داریم که از حاصل ضرب این دو، 36 حالت به وجود میآید. در نتیجه، \(\Large n(S)=36\) است. بنابراین احتمال اینکه در هر دو پرتاب مضرب 3 مشاهده کنیم، برابر است با:
\(\LARGE P(A)=\frac{n(A)}{n(S)}=\frac{4}{36}=\frac{1}{9}\)
به مثال بعدی از مبحث مجموعه ها و احتمال ریاضی نهم دقت کنید.
مثال بیرون کشیدن کارت
مثال 4: داخل جعبهای، 20 کارت با شمارههای 1 تا 20 قرار دادیم. اگر یک کارت به تصادف از جعبه برداریم، احتمال اینکه شمارۀ کارت، عدد اول باشد چه قدر است؟
حل: فضای نمونه برابر است با:
\(\Large S=\{1, 2, \dots, 20\}\)
پیشامد مطلوب که همان اعداد اول بین 1 تا 20 است، برابر است با:
\(\Large A=\{2, 3, 5, 7, 11, 13, 17, 19\}\)
بنابراین، احتمال رخدادن پیشامد \(\Large A\) برابر است با:
\(\LARGE P(A)=\frac{n(A)}{n(S)}=\frac{8}{20}=\frac{2}{5}\)
به مثال بعدی از مبحث مجموعه ها و احتمال ریاضی نهم دقت کنید.
مثال فرزندان خانواده
مثال 5: خانوادهای دارای دو فرزند است. احتمال اینکه فرزند کوچکتر دختر باشد چه قدر است؟
حل: به روشهای مختلف میتوان این مساله را حل کرد. همین طور به سادگی میتوان پیش بینی کرد که احتمال پیشامد مطلوب، \(\Large \frac{1}{2}\) است؛ اما برای تمرین، فضای نمونه و پیشامد را به دست میآوریم. دختر را با \(\Large G\) و پسر را با \(\Large B\) نشان میدهیم. اگر مولفۀ اول زوج مرتب، فرزند بزرگتر و مولفۀ دوم زوج مرتب، فرزندکوچکتر باشد، فضای نمونه برابر است با:
\(S=\{(F, F), (B, B), (F, B), (B, F)\}\)
پیشامد مطلوب ما که همان دختر بودن فرزند کوچکتر است، برابر است با:
\(\Large A=\{(F, F), (B, F)\}\)
میتوانیم \(\Large S\) و \(\Large A\) را با استفاده از نمودار وِن نیز به صورت زیر نمایش دهیم:
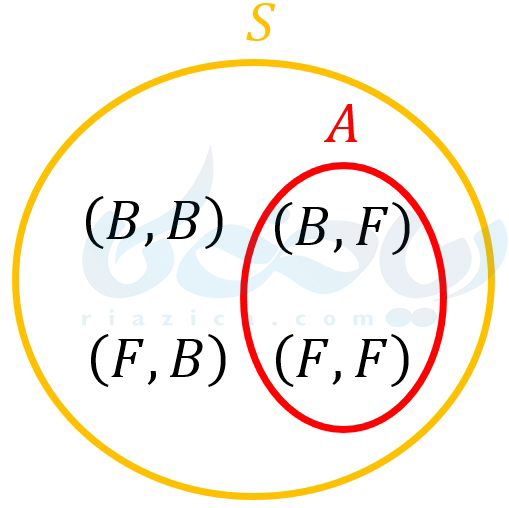
بنابراین، احتمال رخدادن پیشامد \(\Large A\) برابر است با:
\(\LARGE P(A)=\frac{n(A)}{n(S)}=\frac{2}{4}=\frac{1}{2}\)
زنگ آخر کلاس مجموعه ها و احتمال ریاضی نهم
در درسنامهای که مربوط به ریاضی نهم بود خواندیم، به بررسی مبحث مجموعهها و احتمال ریاضی نهم پرداختیم. همانطور که دیدد، احتمال رخ دادن یک پیشامد را میتوان با استفاده از تقسیم تعداد اعضای دو مجموعه به دست آورد. مثالهایی که از این مبحث حل کردیم به شما در درک این مبحث کمک خواهد کرد.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث مجموعهها و احتمال ریاضی نهم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





سلام
این سوال را چطور باید پاسخ داد؟
-به طور اتفاقی دو حروف از حروف البای فارسی انتخاب میکنیم ، با چه احتمالی از حروف شما خواهد بود؟
سلام و عرض ادب
می شود ۲/۳۲ .
موفق باشید.
حروف شما سه تا هست و باید دوتا ازش انتخاب کنیم پس میشه ترکیب ۲از ۳ برای صورت و مخرج هم میشه ۳۲
پس جواب میشه ۳/۳۲
سلام وعرض ادب درسته دوست عزیز چون کلمه شما رو داخل پرانتزننوشته بودند وسوالشون زیر پست نهمبود باعث برداشت اشتباه شد ممنون از دقت نظر شما
عالی بود
اگه انتخاب یک حرف باشه میشه ۳/۳۲
وقتی دو حرف انتخاب کنیم پس احتمالمون هم دوبرابر میشه.
فکر میکنم جوابمون ۶/۳۲ باشه.
با سلام واحترام
از بین سه حرف میخواهیم فقط دو حرف را انتخاب کنیم نه اینکه کلمه بنویسیم پس انتخاب دو از سه میشود که جواب ۳ میشود
سلام.کاملا درست میفرمایید.تشکر از پاسخگویی و توضیحاتتون.خدا بهتون خیر بده.
سلام در پرتاب یک تاس و یک سکه :
چقد احتمال دارد سکه رو یا تاس عدد زوج بیاید
چقد احتمال دارد سکه رو و تای عدد زوج بیاید
با سلام وعرض ادب
اولی چون یا اومده اجتماع دو مجموعه هست پس میشه نه یازدهم ودومی چون و اومده میشه اشتراک پس میشه سه دوازدهم
سلام خسته نباشید ببخشید جواب این سوال چی میشه؟:
احتمال آن که علی در فصل تابستان به دنیا آمده چقدر است؟
با سلام دوست عزیز
میشه یک چهارم
ممنون بابت سایت خوبتون
با سلام واحترام
ممنون حسن اتخاب شما
باسلام و درود ، میشود این سوال را توضیح بدهید.
من این سوال را بلد نیستم.
★ – هـــر یـــک از ارقــــام ۱ و ۲ و ۳ و ۴ و ۵ را روی پـــــنج کـــارت یکسان نوشته ایـــم ، به تصــــادف یـــک کـــارت را بیــــرون کشـــیده، ســــپس کـــارت دیگـــری از بقیـــه بیــــرون مـــی کشـــیم. بــا کـــدام احتمال شمارههای این دو کارت اعداد متوالی هستند؟
اگر در اینجا نتوانستید توضیح بدهید ، در واتساپ به این شماره 09212318760 توضیح دهید.
ممنون می شوم اگر ، جواب سوال مرا ، جواب دهید ، فقط با توضیح.
سلام خانمون از ما خواست تا بریم احتمال تاس رو بنویسم ولی من هری میگردم نمیتونم جوابه خوبی برای سوال پیدا کنم ??
سلام وقتتون بخیر خیلی خوب بود مرسی ?
با سلام وادب
خدا رو شکر که پستهای ما رو دوست داشتید
میشه ساده تر توضیح بدید
با سلام وادب
از این ساده تر؟؟؟
بسیار عالی، پیشنهاد میکنم استفاده کنید از مطالب بسیار خوبش☺️☺️☺️?
با سلام وادب
ممنون دوست عزیز معرف سایت ما به دوستانتون باشید
سلام خیلی ممنون از سایت خوبتون واقعا عالی هست و جای هیچ سوالی رو نمیزاره حتما به دوستام معرفی میکنم ❤?
با سلام وادب
ممنون از نظرلطف شما وخوشحالیم که مفید بوده
سلام خیلی ممنون از سایت خوبتون واقعا حرف نداشت و جای هیچ سوالی باقی نمیمونه
بازم ممنونمممم ❤
سلام و عرض ادب
ببخشید وقتی میگه از ۱تا۹کارت احتمال اینکه پیشامد عدد اول باشد چقدر می تواند باشد؟
سلام و عرض ادب
در سوالی گفته شده اگر سه سکه را باهم پرتاب کنیم احتمال اینکه حداکثر یکی از سکه ها رو بیاید چقدر است ؟
سلام دوست عزیز
یک دوم
سلام برای این سوال : خانواده ای دو فرزند دارند احتمال اینکه هردو فرزند این خانواده دختر باشند چقدر است؟ چطور باید حساب کنیم؟
با سلام دوست عزیز
یک چهارم میشه چون چهار حالت داریم
سلام خسته نباشید من یک سوال دارم در پرتاب همزمان تاس آبی و قرمز احتمال آنکه اعداد ۳ یا ۴ یا هردو ظاهر شوند را حساب کنید
با سلام و ادب
اگه تمام حالتها رو بنویسید برای دوتاس ۳۶ حالت هست که دوازده تای آنها ۳یا ۴ یا هردو اومده پس جواب بعد ساده شدن میشه یک سوم
سلام لطفا اینارو واسم توصیح بدید من تو اینا اشکال دارم
اگر تاس و سکه ای را همزمان بیندازیم چقدر احتمال دارد:
الف) تاس عددی زوج و سکه پشت باشد
ب) تاس مضرب ۲ و سکه رو باشد
سلام دوست عزیز
کافیست فضای نمونه که همون تمام حالات ممکن هست رو بنویسید مثلا تاس ۱ وسکه رو تا آخر که جمعا ۱۲ حالت میشه وبعد به سوالات جواب بدید
سکه ای را ۵ بار پرتاب میکنیم.میدانیم حدافل دو بار رو آمده است.احتمال اینکه دقیقا ۴ بار رو بیاید چقدر است؟
ممنون میشم اگر جواب بدین
سلام این احتمال شرطی هست فضای نمونه جدید شما ۲۶ عضو دارد یعنی از ۳۲ حالت کلی ۲۶ حالت حداقل دو بار رو میاید حال خواسته احتمال اینکه دقیقا ۴ بار روبیاید را بیابیم میشود پنج بیست وششم
احتمال صید مروارید در جویبار کوچکی که به برکه میریزد چقدر است؟
سلام دوست عزی اگه منظورتون اینه که این احتمال رو با عدد خاصی بگیم نمیشه چون باید تعداد مروایدهای موجود ومقدار آب جری در جویبار رو بدونیم
هیچ صیادی در جوی حقیری که به گودالی میریزد مرواریدی صید نخواهد کرد.جمله ای از کتاب حکایت دولت و فرزانگی
سلام چه جواب جالبی
سلام من بخواهم از ۱ تا ۳۶ عدد رو انتخاب کنم کدام اعداد شانس بیشتری دارند
سلام دوست عزيز
احتمال انتخاب همه یک سی وششم هست ولی به نظرم ما ناخودآگاه اعداد اول وآخر رو بیشتر انتخاب میکنیم ولی دقیق نمیدانم
۵ عدد میخواهم از ۱ تا ۳۶ انتخاب کنم کدام اعداد رو باید انتخاب کنم که شانس بیشتری داشته باشن