آموزش ریاضی پایه نهم
معرفی مجموعه ریاضی نهم 👣🅰️ – گام به گام با مثال!
میخواهیم به مبحث معرفی مجموعه ریاضی نهم بپردازیم. مبحث بسیار ساده اما در عین حال بسیار جذاب! سعی کردیم طوری درسنامه را پیش ببریم تا با مطالعۀ آن، بر تمام مباحث درس مسلط شوید. هر سوالی هم که داشتید میتوانید در قسمت دیگاهها مطرح کنید. به سرعت به سوالتان پاسخ خواهیمداد.
مجموعه چیست؟
از گرد هم آمدن دستهای از اشیا با دو ویژگی:
- مشخص بودن
- متمایز بودن
مجموعه تشکیل می شود. دقت کنید، ترتیب قرار گرفتن اشیا در مجموعه اهمیتی ندارد. منظور از متمایز بودن این است که در یک مجموعه عضو تکراری نداریم اگر در مجموعهای عضوی تکرار شود یکبار شمرده می شود.. اما مشخص بودن به چه معنی است؟ برای یافتن جواب این سوال، به مثالهای زیر از درس معرفی مجموعه ریاضی نهم دقت کنید.
مثال از مجموعه در معرفی مجموعه ریاضی نهم
مثال 1: آیا عبارت “دو تن از شاعران معروف ایران” بیانگر یک مجموعه است؟
حل: خیر؛ زیرا انتخابهای متفاوتی وجود دارد. به عبارت دیگر به صورت یکتا نمیتوان اعضایی را مشخص کرد که در جملۀ بالا صدق کنند. میتوان فردوسی و حافظ را در نظر گرفت، یا حافظ و سعدی و یا بسیاری از حالتهای دیگر.
مثال 2: کدام یک از دو عبارت زیر مشخص کنندۀ یک مجموعه است؟
- الف) دو عدد طبیعیِ کوچکتر از 4
- ب) اعداد طبیعیِ کوچکتر از 4
حل: اشیایی که در عبارت “الف” بیان شدهاند، مشخص و یکتا نیستند. به عبارت دیگر هم میتوان 1 و 2 را در نظر گرفت، هم 2 و 3 و هم 1 و 3. اما اشیای عبارت “ب”، مشخص و یکتا هستند. یعنی فقط اعداد 1 و 2 و 3، اشیای متناظر با عبارت “ب” محسوب میشوند. همچنین به وضوح، تمام اعداد 1 و 2 و 3 متمایزند.
برای علاقهمندان (خارج از کتاب): مجموعه به طور دقیق با استفاده از اصول موضوعه مشخص میشود. اصول موضوعه به طور شهودی عباراتی هستند که بدون اثبات بر سر آنها توافق میشود تا به عنوان پایهای برای اثبات گزارهها، قضایا و لِمها قرار گیرند. در صورتی که علاقهمندید میتوانید اصول موضوعۀ زرملو-فرانکل و اصل موضوع انتخاب را مطالعه کنید. در ادامه چگونگی نمایش مجموعه را در درس معرفی مجموعه ریاضی نهم خواهیم دید.
نمایش مجموعه
اعضای یک مجموعه را بین دو ابرو (آکولاد) قرار میدهیم. مثلاً مجموعۀ اعداد طبیعیِ کوچکتر از 4 برابر است با \(\Large \{1, 2, 3\}\). همچنین برای اینکه نشان دهیم شیئی عضو یک مجموعه است، از علامت \(\Large \in\) استفاده میکنیم. به طور مثال، اگر \(\Large A=\{1, 3\}\)، مینویسیم \(\Large 1 \in A\) و میخوانیم “1 عضو \(\Large A\) است”. برای نشان دادن عدم عضویت نیز، از علامت \(\Large \not\in\) استفاده میکنیم. مثلاً مینویسیم \(\Large 4\not\in A\) و میخوانیم “4 عضو \(\Large A\) نیست”. به مثال زیر از درس معرفی مجموعه ریاضی نهم دقت کنید.
مثال از نمایش مجموعه
مثال 2: هر یک از عبارتهای زیر، نشان دهندۀ چه مجموعهای است؟
- الف) اعداد اول زوج
- ب) جوابهای صحیح معادلۀ \(\Large x+2=-3\)
- ج) شمارندههای طبیعی عدد 12
حل: تنها عدد اول زوج، 2 است. پس، عبارت “الف” بیانگر مجموعۀ \(\Large \{2\}\) است. جواب معادلۀ \(\Large x+2=-3\) برابر با \(\Large -5\) است که یک عدد صحیح است. بنابراین، عبارت “ب” بیانگر مجموعۀ \(\Large \{-5\}\) است. شمارندههای طبیعی عدد 12 نیز، اعداد 1، 2، 3، 4، 6، 12 هستند. پس، عبارت “ج” بیانگر مجموعۀ \(\Large \{1, 2, 3, 4, 6, 12\}\) است.
نمودار ون
مبحث مهم دیگر در درس معرفی مجموعه ریاضی نهم ، نمودار ون است. برای نشان دادن یک مجموعه میتوان از یک خم سادۀ بسته استفاده کرد. به این نوع نمایش مجموعهها، نمودار وِن میگویند. به طور مثال، اگر \(\Large B=\{1, 2, 5\}\) باشد، نمودار ون آن برابر است با:
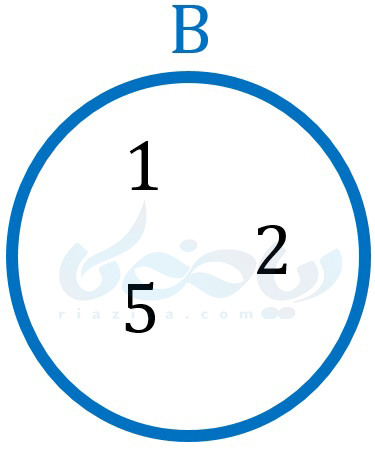
همچنین میتوان دو یا چند مجموعه را در یک نمودار ون نمایش داد. در این حالت، اشیایی که بین دو یا چند مجموعه مشترک هستند، در ناحیۀ مشترک بین آن چند مجموعه قرار میگیرند. به مثال زیر از درس معرفی مجموعه ریاضی نهم توجه کنید.
مثال از رسم نمودار ون در معرفی مجموعه ریاضی نهم
مثال 3: اگر \(\Large A=\{1, 2, 4\}\) و \(\Large B=\{3, 4, 5\}\) باشد، \(\Large A\) و \(\Large B\) را در یک نمودار ون نشان دهید.
حل: نمودار ون برای این دو مجموعه به صورت زیر در میآید:
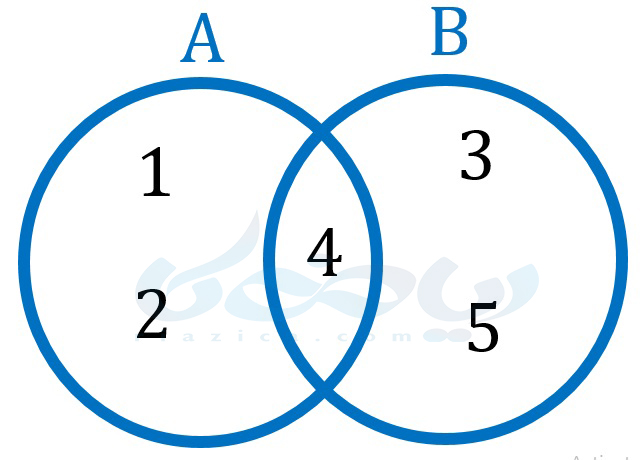
همانطور که میبینید، از آنجاییکه عدد 4 بین دو مجموعه مشترک است، در ناحیۀ مشترک بین \(\Large A\) و \(\Large B\) رسم شده است.
مجموعۀ تهی
اگر یک مجموعه هیچ عضوی نداشته باشد، به آن، مجموعۀ تهی گفته و آن را با نماد \(\Large \emptyset\) یا \(\Large \{\}\) نمایش میدهیم. باید دقت داشت که مجموعۀ \(\Large \{\emptyset\}\) یا هر مجموعۀ دیگری که بین دو آکولاد دارای یک عضو باشد، مجموعۀ تهی نیست، بلکه تک عضوی است. به مثال زیر از درس معرفی مجموعه ریاضی نهم توجه کنید.
مثال 4: کدام یک از عبارتهای زیر، نشان دهندۀ مجموعۀ تهی است؟
- الف) مجموعۀ اعداد صحیح نامنفی کوچکتر از 1
- ب) مجموعۀ اعداد صحیح منفی بزرگتر از 0
حل: عبارت “الف” بیانگر مجموعۀ \(\Large \{0\}\) است که یک مجموعۀ تک عضوی است. اما هیچ عدد صحیح منفی بزرگتر از صفر وجود ندارد. بنابراین عبارت “ب” نشان دهندۀ مجموعۀ تهی است.
زنگ آخر کلاس معرفی مجموعه ریاضی نهم
در درسنامهای که مربوط به ریاضی نهم خواندیم، مجموعهها را معرفی کردیم. روش نمایش یک مجموعه و اعضای آن را بررسی کردیم. همانطور که دیدیم میتوان یک یا چند مجموعه را با نمودار وِن نیز نمایش داد. در انتها نیز، مجموعۀ تهی را معرفی کردیم و گفتیم مجموعهای که عضوی نداشته باشد، مجموعۀ تهی است.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث معرفی مجموعه ریاضی نهم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





عالی بود
با سلام واحترام
ممنون از نظر خوب شما
عالیه
با سلام
ممنونم
ممنونم از اساتید ریاضیکا
با سلام
ممنون دوست عزیز
عالی بود ??
با سلام واحترام
ممنون از توجه شما
عالیییی
با سلام
الحمدالله که دوست داشتید
سلام ببخشید میخواستم بدونم که چه شکلی نمودار ون و رسم کنیم
با سلام واحترام
کافیهیه خم بسته یا یه دایره بکشید وداخلش اعضای مجموعه رو بنویسید حال اگه دو تا مجموعه باشند قسمت مشترک رو روی هم میکشیم
سلام یه سوال، گفته که بجای x عددی قرار دهید که مجموعه{xو3_} دارای یک عضو باشد، باید چیکارش کنیم
با سلام وادب
خوب فقط منفی سه رو میتونید بذارید
لطفابیشتربذاریدعالی بودولی
با سلام ولی چی؟
سلام داداش با شکل دایره باید نمودار ون رسم کنی
با سلام
بله برادر البته به شکل بیضی بیشتر میکشند ولی دایره هم بکشید اشکال نداره
سلام هر مجموعه زیر مجموعه چی است؟
با سلام و عرض ادب
هر مجموعه زیر مجموعه خودش میباشد ؛و مجموعه تهی ریرمجموعه همه مجموعه هاست
سلام منظور از سه شمارنده اول متمایز دارد چی هست
با سلام وادب
یعنی سه تا شمارنده یا همون مقسوم علیه اول مختلف
متمایز یعنی غیر تکراری
سلام . ببخشید آیا دو مجموعه زیر مساوی هستند ؟
A={{a,b},c,b}
B={a,b,c}
با سلام و عرض ادب
خیر مساوی نیستند چون یکی از اعضای مجموعه A خودش محموعه ای شامل دو عضو میباشد
سلام
مجموعه ( سیب و شکل سیب و apple ) چند عضو دارد
با سلام وعرض ادب
این سوال اصلا سوال خوبی نیست هر سه شکل دارد سیب را نشان میدهد پس یک عضو دارد
سلام
نمیشه بگیم سه عضو داره؟ چون متفاوتن از نظر شکل
با سلام
گفتم این سوال تالیفی خوبی نیست به نظر مولف بستگی داره
سلام مجموعه [ apple_ سیب _ ?] چند عضو دارد
یک عضو
سلام
ایا فوتبالیست های حرفه ای ایران
و شاعران معروف ایران
تشکیل مجموعه می دهند؟
با سلام وعرض ادب
خیر چون معروف بودن وحرفه ای بودن از دید هر کس فرق میکند واعضای این مجموعه ها مشخص ومعلوم نیست
لطفا چندین مثال برای مجموعه ها بزنید، سپاس
با سلام
انشالله در آینده نزدیک
سلام میشه نمایش صورت ریاضی مجموعه رو درموردش کمی توضیح بدید
سلام از نماد های ریاضی مثال بزنید
با سلام
مثلا نمادهایی که برای نشان دادن مجموعه ها به کار میبریم یا علامت عضویت یا نماد بزرگتری وکوچکتری
میشه بگید مجموعه ی متناظر چی؟
مجموعه ی یکتا چی؟
با سلام وادب
منظورتون از مجموعه متناظر رو نمیدونم چیه ولی یکتا بودن یک مجموعه یعنی مشخص بودن اعضای مجموعه مثلا وقتی می گوییم سه تناز شعرای معروف این مجموعه یکتا نیست چون از نظر اشخاص مختلف معروفیت نسبی هست ولی وقتی میگوییم وزرای کابینهدولت سیزدهماعضایآن کاملا مشخص است ویکتا هست
عالی
عالی بود
سلام وقت بخیر
مجموعه یکتا چیه؟
با سلام وادب
مجموعه ای که فقط یک عضو دارد
بهترین سایت ریاضی
عالیه
با سلام وادب
چون توسط دبیری که خودش این مباحث رو تدریس کرده وبا آموزش وچالشهاش روبه رو بوده نوشته شده ممنون از نگاه شما
نیمساز خطی هست که از راس شروع شده و زاویه را به دو قسمت مساوی تقسیم میکند???
خیلی خوب بود
با سلام وادب
ممنون از نظر لطف شما
سعی کنید مطالب کامل تر باشه
با سلام
دوست عزیز از چه نظر کاملتر بشه؟
ببخشید اگر مجموعه{1و۲و۳و۴ }=A
{3}عضو مجوعهAاست.
یا ۳ عضو مجوعه A است
آیا اکولاد تاثیری دارد؟
با سلام وادب
۳عضو مجموعه A است وقتی آکولاد میذارید میشه یه عضو جدید
این مجموعه چند عضو داره؟
{6و {7و۹}}
با سلام وادب
دو عضو
عالی. دمتون گرم به خاطر توضیحات متنی عالیتون. ممنون. خسته نباشید.
با سلام دوست عزیز
ممنون از انرژی که به ما میدهید
سلام. ایا میتوان در مجموعه A,B مثال زد که: A-B= B-A
با سلام دوست عزیز
وقتی دومجموعه با هم برابر باشن
سلام خسته نباشین خدمت اساتید گرامی. یه سوال داشتم خواستم ببینم صفحهz=0 یکتا است؟چرا؟
سلام دوست عزیز،
خیلی ممنونیم که سوالتان را با ما در میان گذاشتید.
اگرچه به صورت شهودی یکتا بودن صفحهٔ z=0 مشخص است اما برای اثبات ریاضی، شهود کافی نیست. بنابراین به سوال شما باید این طور پاسخ دهیم:
برای اینکه ثابت کنیم صفحهٔ z=0 یکتاست، میتوانید از برهان خلف استفاده کنید. فرض میکنیم صفحهٔ z=0 یکتا نیست. پس صفحهٔ دیگری مانند z’=0 وجود دارد که از صفحهٔ z=0 متمایز است. در نتیجه یا حداقل یک نقطه در صفحهٔ z=0 است که در صفحهٔ z’=0 وجود ندارد و یا حداقل یک نقطه در صفحهٔ z’=0 است که در صفحهٔ z=0 وجود ندارد. بدون کاستن از کلیت مسئله، فرض میکنیم نقطهای در صفحهٔ z=0 هست که در صفحهٔ z’=0 وجود ندارد. اسم این نقطه را b میگذاریم. دو حالت وجود دارد؛ یا مختصات z نقطهٔ b برابر با صفر نیست که در این صورت از آنجاییکه b را در صفحهٔ z=0 در نظر گرفته بودیم به تناقض میرسیم. یا مختصات z نقطهٔ b برابر با صفر است. در این صورت نقطهٔ b هم در صفحهٔ z=0 قرار دارد و هم در صفحهٔ z’=0. باز هم به تناقض رسیدیم؛ زیرا فرضمان این بود که نقطهٔ b در صفحهٔ z’=0 قرار ندارد. بنابراین فرضمان مبنی بر یکتا نبودن صفحهٔ z=0 اشتباه بوده است. پس صفحهٔ z=0 یکتاست.
بسیار بسیار عالی و پرکاربرد🙃👌
سلام دوست عزیز
خدا رو شکر مفید بوده