آموزش ریاضی پایه نهم
مجموعه های برابر ریاضی نهم ⏸✏️ – توضیح کامل با مثال!
شهریور
در این درسنامه قصد داریم تا به مبحث مجموعه های برابر ریاضی نهم بپردازیم. در انتهای این درسنامه، به راحتی آب خوردن می‌توانید به سوالات زیر پاسخ دهید:
- چه زمانی مجموعه های برابر داریم؟
- زیرمجموعه چیست؟
- نمایش مجموعه های اعداد چگونه است؟
دو مجموعۀ برابر در مبحث مجموعه های برابر ریاضی نهم
اگر دو مجموعۀ \( \Large A \) و \( \Large B \) داشته باشیم به طوری که هر عضو \( \Large A \)، عضوی از \( \Large B \) و هر عضو \( \Large B \)، عضوی از \( \Large A \) باشد، می‌گوییم دو مجموعۀ \( \Large A \) و \( \Large B\) با هم برابرند و می‌نویسیم \( \Large A=B \). به زبان ساده تر، هر گاه اعضای دو مجموعه یکسان باشند، دو مجموعه با هم برابرند. دقت کنید، ترتیب اعضا در یک مجموعه برایمان مهم نیست. به طور مثال مجموعۀ \( \Large A=\{1, 2, 3\} \) با مجموعۀ \( \Large B=\{3, 2, 1\} \) برابر است.
اگر عضوی از \( \Large A \) باشد که در \( \Large B \) نباشد یا عضوی از \( \Large B \) باشد که در \( \Large A \) نباشد، دو مجموعۀ \( \Large A \) و \( \Large B \) برابر نیستند. در این صورت می‌نویسیم \( \Large A\neq B \). به مثال زیر از مجموعه های برابر ریاضی نهم دقت کنید.
مثال از مجموعه های برابر ریاضی نهم
مثال 1: اگر \( \Large A=\{1, 3, m, 8\} \) و \( \Large B=\{8, 1, n, 4\} \) باشد، مقدار \( \Large m \) و \( \Large n \) را طوری تعیین کنید که داشته باشیم \( \Large A=B \).
حل: از آنجاییکه \( \Large A=B \)، هرعضو \( \Large A \) باید عضوی از \( \Large B \) باشد. پس، عدد 3 باید عضوی از \( \Large B \) باشد. در نتیجه \( \Large n=3 \). از طرفی هر عضو \( \Large B \) نیز باید عضوی از \( \Large A \) باشد. بنابرین، عدد 4 عضو \( \Large A \) است. پس \( \Large m=4 \). در نتیجه داریم:
\( \LARGE A=B=\{1, 4, 3, 8\} \)
زیرمجموعه
مبحث دیگر مجموعه های برابر ریاضی نهم ، مبحث زیرمجموعه است. اگر دو مجموعۀ \( \Large A \) و \( \Large B \) داشته باشیم به طوری که هر عضو \( \Large A \)، عضوی از \( \Large B \) باشد، می‌گوییم \( \Large A \) زیرمجموعۀ \( \Large B \) است و می‌نویسیم \( \Large A \subseteq B \). مثلاً \( \Large A=\{1, 2\} \) زیرمجموعۀ \( \Large B=\{1, 2, 3\} \) است. طبیعی است اگر عضوی در \( \Large A \) باشد که در \( \Large B \) نباشد، می‌گوییم \( \Large A \) زیرمجموعۀ \( \Large B \) نیست و می‌نویسیم \( \Large A \not\subseteq B \). با توجه به تعریفی که کردیم، دو گزارۀ زیر را می‌توان به راحتی نتیجه گرفت:
- الف) هر مجموعه‌ای زیرمجموعۀ خودش است. یعنی \( \Large A \subseteq A \).
- ب) هر دو مجموعۀ برابر، زیرمجموعۀ یکدیگر هستند.
اثبات گزارۀ “الف” که بدیهی است. چون هر عضوی از یک مجموعه، عضو خود آن مجموعه است. برای اثبات گزارۀ “ب” نیز، اگر دو مجموعۀ \( \Large A \) و \( \Large B \) با یکدیگر برابر باشند، هر عضوی از \( \Large A \) در \( \Large B \) هست. پس \( \Large A \subseteq B \). هر عضوی از \( \Large B \) نیز در \( \Large A \) هست. پس \( \Large B\subseteq A \).
زیرمجموعۀ تهی
دو مجموعۀ \( \Large A \) و \( \Large B \) را در نظر بگیرید. اگر برای هر \( \Large x\in A \) داشته باشیم \( \Large x \in B \)، می‌گوییم \( \Large A \subseteq B \). حالا یک سوال مهم! اگر مجموعۀ ی \( \Large A \) هیچ عضوی نداشته باشد، گزارۀ قبل در مورد آن صادق است؟ پاسخ مثبت است. چون مجموعۀ \( \Large A \) هیچ عضوی ندارد در گزاره صدق می‌کند. بنابراین تهی زیرمجموعۀ هر مجموعۀ دلخواهی است.
برای علاقه‌مندان (خارج از کتاب): روش دیگر اثبات این قضیه، استفاده از برهان خلف است. فرض کنیم مجموعه‌ای مثل \( \Large A \) وجود دارد که تهی زیرمجموعۀ آن نیست. در این صورت عضوی از تهی وجود دارد که در \( \Large A \) نیست. اما تهی هیچ عضوی ندارد. به تناقض رسیدیم. در نتیجه تهی زیرمجموعۀ هر مجموعۀ دلخواهی است.
به مثال زیر از درس مجموعه های برابر ریاضی نهم دقت کنید.
مثال از زیرمجموعه‌ها
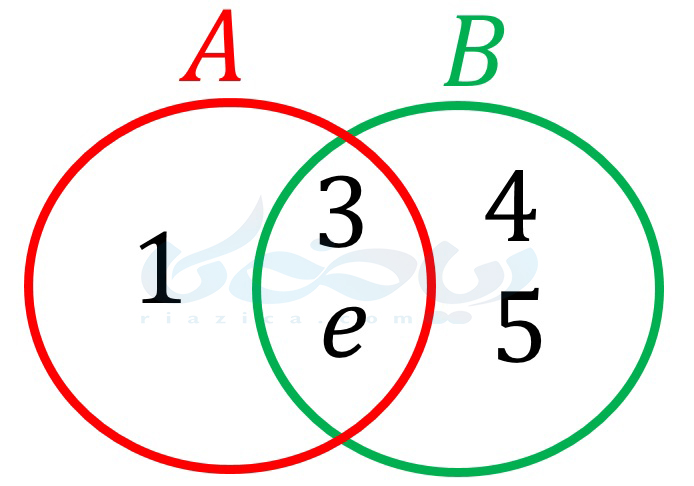
مثال 2: ثابت کنید \( \Large A=\{1, 3, e\} \) زیرمجموعۀ \( \Large B=\{e, 3, 4, 5\} \) نیست. نمودار ون آن‌ها را در یک شکل رسم کنید.
حل: در مجموعۀ \( \Large A \)، عدد 1 وجود دارد که در مجموعۀ \( \Large B \) نیست. بنابراین \( \Large A \not\subseteq B \). نمودار ون این دو مجموعه در شکل زیر رسم شده است.
مثال 3: مجموعۀ \( \Large E=\{1, 2\} \) چند زیرمجموعه دارد؟
حل: زیرمجموعه‌های \( \Large E\) به صورت زیر هستند:
\( \LARGE E_1=\{1\} \)
\( \LARGE E_2=\{2\} \)
\( \LARGE E_3=\{1, 2\} \)
\( \LARGE E_4=\emptyset \)
نمودار ون مجموعۀ \( \Large E\) به همراه زیرمجموعه‌های \( \Large E_1\) تا \( \Large E_3\) در شکل زیر رسم شده است.
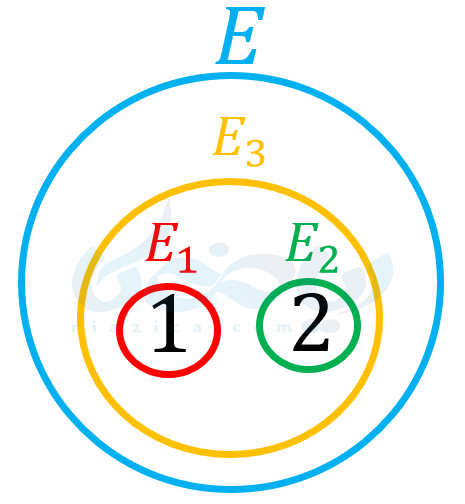
به طور کلی اگر یک مجموعه \( \Large n\) عضو داشته باشد، \( \Large 2^n\) زیرمجموعه خواهد داشت؛ زیرا فرض کنید می‌خواهیم یک زیرمجموعه از مجموعۀ دلخواه \( \Large A\) بنویسیم. اسم این زیرمجموعه را \( \Large A_1\) می‌گذاریم. برای هر عضو \( \Large A\) دو حالت داریم. یا آن عضو را در \( \Large A_1\) قرار می‌دهیم یا نه. بنابراین اگر \( \Large n\) عضو در مجموعۀ \( \Large A\) وجود داشته باشد، \( \Large 2^n\) انتخاب یا به عبارتی \( \Large 2^n\) زیرمجموعه خواهیم داشت.
حالا شما بگویید اگر مجموعه ای ۵ عضو داشته باشد چند زیر مجموعه دارد؟
نمایش مجموعه‌های اعداد
مبحث آخر از درس مجموعه های برابر ریاضی نهم ، مبحث نمایش مجموعه هاست. در سال‌های گذشته با اعداد طبیعی، اعداد حسابی و اعداد صحیح آشنا شده‌اید. هر دسته از این اعداد تشکیل یک مجموعه داده و با نمادهای زیر مشخص می‌شوند:
- مجموعۀ اعداد طبیعی را با نماد \( \Large \mathbb{N}\) نشان می‌دهیم و داریم: \( \Large \mathbb{N}=\{1, 2, 3, \dots\}\)
- مجموعۀ اعداد حسابی را با نماد \( \Large W\) نشان می‌دهیم و داریم: \( \Large W=\{0, 1, 2, 3, \dots\}\)
- مجموعۀ اعداد صحیح را با نماد \( \Large \mathbb{Z}\) نشان می‌دهیم و داریم: \( \Large \mathbb{Z}=\{\dots, -2, -1, 0, 1, 2, \dots\}\)
از آنجاییکه مجموعۀ اعداد طبیعی، زیرمجموعۀ اعداد حسابی و مجموعۀ اعداد حسابی، زیرمجموعۀ اعداد صحیح است، داریم:
\( \Large \mathbb{N}\subseteq W \subseteq \mathbb{Z}\)
نمایش مجموعه با نماد ریاضی
برای نمایش مجموعه‌ها می‌توانیم از نمادهای ریاضی نیز استفاده کنیم. به طور مثال، مجموعۀ \( \Large F=\{3, 4, 5\}\) را در نظر بگیرید. مجموعۀ \( \Large F\)، مجموعۀ اعداد طبیعی بین 2 و 6 است. می‌توانیم این مجموعه را به صورت زیر نمایش دهیم:
\( \LARGE F=\{x\in \mathbb{N}|2<x<6\}\)
در عبارت بالا، علامت “|” را “به طوری که” می‌خوانیم. یعنی مجموعۀ \( \Large F\) برابر است با \( \Large x\)های طبیعی به طوری که \( \Large x\) بین 2 و 6 باشد. به مثال‌های زیر از درس مجموعه های برابر ریاضی نهم دقت کنید.
مثال از نمایش مجموعه با نماد ریاضی در مبحث مجموعه های برابر ریاضی نهم
مثال 4: مجموعۀ اعداد طبیعی زوج و فرد را با استفاده از نمادهای ریاضی نمایش دهید.
حل: مجموعۀ اعداد طبیعی زوج را با \( \Large E\) و فرد را با \( \Large O\) نشان می‌دهیم (E حرف ابتدایی کلمۀ Even به معنای زوج و O حرف ابتدایی کلمۀ Odd به معنای فرد است). نمایش این دو مجموعه با استفاده از نمادهای ریاضی به صورت زیر است:
\( \LARGE E=\{2k|k \in \mathbb{N}\}\)
\( \LARGE O=\{2k-1|k \in \mathbb{N}\}\)
مثال 5: مجموعۀ \( \Large M=\{x\in \mathbb{Z}| x^2<5\}\) را با استفاده از نمایش اعضای آن بازنویسی کنید.
حل: مجموعۀ \( \Large M\)، مجموعۀ \( \Large x\)های صحیح است به طوری که مربع \( \Large x\) کوچکتر از 5 باشد. بنابراین مجموعۀ \( \Large M\) برابر است با:
\( \Large M=\{-2, -1, 0, 1, 2\}\)
زنگ آخر کلاس مجموعه های برابر ریاضی نهم
در درسنامه‌ای که مربوط به ریاضی نهم خواندیم، ابتدا بررسی کردیم دو مجموعه در چه شرایطی با یکدیگر برابر هستند. سپس، زیر مجموعه‌ها را معرفی کردیم. در انتها مجموعه‌های اعداد را بررسی کرده و نشان دادیم که چگونه می‌توان با استفاده از نمادهای ریاضی، یک مجموعه را نمایش داد.
ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث مجموعه های برابر ریاضی نهم دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.
ممنون عالی بود
با سلام وعرض ادب
ممنون از لظف شما
{1,2}=A زیر مجموعه‌ی {1,2}=B هست؟
با سلام وعرض ادب
این دومجموعه با هم برابرند وهر مجموعه زیر مجموعه خودش هست پس جواب مثبت هست
اره دیگه
بله
بله هست هر دو مجموعه با هم برابر هستن پس یعنی هر دو زیر مجموعه هم هستن
سلام دوست عزیز
منمون از پاسخگویی شما
????????
باسلام وعرض ادب
????
به به عالی♡
با سلام واحترام
ممنون از نظر لطف شما
خوب بود ?
با سلام واحترام
ممنون از نظر لطف شما
واقعا عالی بود
من فقط یک سوال دارم
a+b در ریاضی به چه معناست
چون این سوال توی مبحث های شما نبود
با سلام وادب در مجموعه عمل جمع نداریم
عالی ممنون
با سلام وادب
ممنون از بذل توجه شما
خیلی خوبه واقعا ادم متوجه میشه
باسلام وادب
هدف ما هم همین بوده ساده کردن ریاضی
اره دیگه
حرف نداشت من که با این توضیح کل فصل رو فهمیدم ممنون♡
با سلام
ممنون از نظر لطف شما
سلام ممنون
سلام
خواهش میکنم
وای دمتون گرم من فردا امتحان داشتم خیلی کمک کرد?♥️
با سلام دوست عزیز
خدا رو شکر مفید بوده
سلام ممنون
فقط x² یعنی چه و چه معنایی میده؟
با سلام وادب
یعنی مجذور یک عدد یا به زبان ساده ضرب یک عدد در خودش
سلام
مرسی از تدریس عالی تون مخصوصا ک جواب x²رو دادین??
سلام و خسته نباشید
آیا مجموعه{۳}با مجموعه{{۳}}برابر است؟
یا سلام وادب
خیر مجموعه اولی در واقع عضو مجموعه دومی هست
یعنی زیر مجموعه دومین آکولاده؟
با سلام
دوست عزیز هر چی که داخل آکولاد قرار بگیره عضو اون مجموعه هست اولی یه مجموعه هست که عضوش ۳ هست دومی یه مجموعه هست که عضوش یه مجموعه هست
عرض ادب
آیا مجموعه{{{}}}} با مجموعه {{فی}} برابر است؟
فی همان مجموعه تهی است
با سلام دوست عزیز
با تعداد آکولادهایی که شما نوشتید برابر نیستن اگه مجموعه اولی که نوشتید غیر از اکولاد اصلی دوتا آکولاد از هر طرف باشه با مجموعه دومی که نوشتید برابر هست
ممنون استاد
بله یکی از آکولادها اضافه هست
خواهش میکنم دوست عزیز
مثال ۵ رو توضیح بدید
با سلام
اعذاذی رو خواسته که مجذورشون از عدد پنج کمتر بشه در جواب هم اعداد صحیحی رو نوشته که توان دوم یا همون مجذورشون از عددپنج کمتر هست