با سلام به شما دوستان ریاضیکا در این پست سعی داریم ابتدا تابع رادیکالی را تعریف کرده سپس طریقه رسم نمودار آن را توضیح میدهیم برای رسم تابع رادیکالی باید ابتدا مفهوم خود تابع رادیکالی را درک کنیم.

تابع رادیکالی

توابع رادیکالی توابعی هستند که در آن‌ها عمل ریشه‌گیری انجام می‌شود. مانند وقتی که طول ضلع یک مربع را می‌خواهیم از روی مساحت آن بدست می‌آوریم در اینصورت داریم:

\( \LARGE a=\sqrt{s} \)

که در آن‌ها \( \Large a \) طول ضلع مربع و \( \Large s \) مساحت مربع می‌باشد. چنین مثال‌هایی ما را بر آن می‌دارد در مورد توابع رادیکالی و نمودار آن‌ها مطالعه بیشتری داشته باشیم.

ساده‌ترین تابع رادیکالی تایع یا ضابطه \( \Large y=\sqrt{x} \) می‌باشد.همانطور که در پست آموزش ریشه گیری دهم خواندیم زیر رادیکال با فرجه زوج باید عدد نامنفی باشد پس دامنه این تایع اعداد حقیقی نامنفی و برد آن نیز اعداد حقیقی نامنفی می‌باشد.

 

\( \LARGE y=\sqrt{x} \)

\( \LARGE D_f=[0,+\infty) \)

\( \LARGE R_f=[0,+\infty) \)

---

---

نمودار \( \Large y=\sqrt{x} \)

مثال ۱ رسم تابع رادیکالی: نمودار تابع \( \Large y=\sqrt{x} \) را رسم کنید.

جواب ۱:اگر با دادن چند مقدار به x نمودار را رسم کنیم با توجه به دامنه آن خواهیم داشت:

 

\( \LARGE 9 \)	\( \LARGE 4 \)	\( \LARGE 3 \)	\( \LARGE 2 \)	\( \LARGE 1 \)	\( \LARGE 0 \)	x
\( \LARGE 3 \)	\( \LARGE 2 \)	\( \Large \sqrt 3 \)	\( \Large \sqrt 2 \)	\( \LARGE 1 \)	\( \LARGE 0 \)	y

 

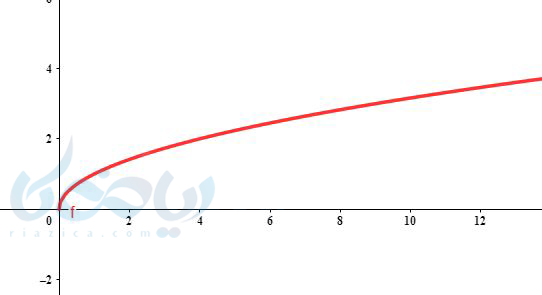
انواع روش‌های رسم تابع رادیکالی

حال اگر بخواهیم نمودار \( \Large y=\sqrt{x+1} \) را رسم کنیم از دو روش می‌توانیم این کار را انجام دهیم.

1. روش نقطه یابی
2. روش انتقال

روش نقطه یابی رسم تابع رادیکالی

در این روش مقادیری که به \( \Large x \) می‌دهیم را با توجه به دامنه تابع طوری انتخاب می‌کنیم که زیر رادیکال عدد مجذور کامل بدست آید تا نقطه یابی راحت صورت گیرد برای اینکار اولین عددی را که انتخاب می کنیم  اولین عدد دامنه است که جذر آن صفر می‌شود و عدد بعدی یک واحد قبل یا بعد آن (با توجه به دامنه) که جذرآن یک می‌شود و عدد سوم را نیز طوری انتخاب می‌ کنیم  که حاصل عبارت زیر رادیکال چهار شود که جذر آن دو که عددی صحیح هست شود

مثال ۲ رسم تابع رادیکالی: نمودار تابع \( \Large y=\sqrt{x+1} \) را رسم کنید.

جواب ۲ به روش نقطه یابی:

 

\( \LARGE y=\sqrt{x+1} \)

دامنه این تابع برابر است با:

\( \LARGE x+1 \geq 0 \)

\( \LARGE x \geq -1 \)

\( \LARGE D_f=[-1,+\infty) \)

\( \LARGE R_f=[0,+\infty) \)

\( \LARGE 3 \)	\( \LARGE 0 \)	\( \LARGE -1 \)	x
\( \LARGE 2 \)	\( \LARGE 1 \)	\( \LARGE 0 \)	y

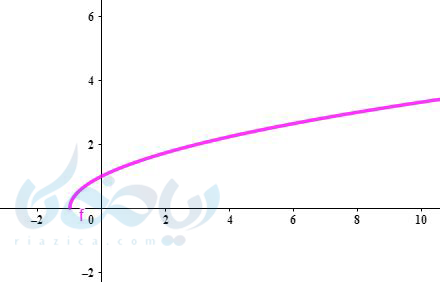
روش انتقال رسم تابع رادیکالی

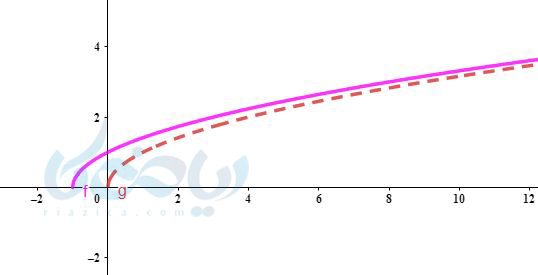
دقت کنید که وقتی نمودار را با روش نقطه یابی رسم کردیم نمودار نسبت به نمودار \( \Large y=\sqrt{x} \) یک واحد به سمت چپ منتقل شد. همانطور که در درسنامه‌های رسم نمودار معادله درجه دوم (سهمی) به روش انتقال و رسم نمودار تابع قدرمطلق به روش انتقال نیز گفته‌ایم به طورکلی:

نمودار \( \Large y=f(x+k) \) در مقایسه با نمودار \( \Large y=f(x) \) اگر \( \Large k>0 \) باشد به اندازه \( \Large k \) روی محور \( \Large x \)ها به سمت چپ منتقل می‌شود و \( \Large k<0 \) باشد به اندازه \( \Large k \) روی محور \( \Large x \) به سمت راست منتقل می‌شود. (انتقال افقی) پس داریم:

جواب ۲ به روش انتقال:

مثال ۳ رسم تابع رادیکالی: نمودار تابع \( \Large y=\sqrt{x-1} \) را رسم کنید.

جواب ۳ به روش نقطه یابی:

 

\( \LARGE y=\sqrt{x-1} \)

دامنه این تابع برابر است با:

\( \LARGE x-1 \geq 0 \)

\( \LARGE x \geq 1 \)

\( \LARGE D_f=[1,+\infty) \)

\( \LARGE R_f=[0,+\infty) \)

\( \LARGE 5 \)	\( \LARGE 2 \)	\( \LARGE 1 \)	x
\( \LARGE 2 \)	\( \LARGE 1 \)	\( \LARGE 0 \)	y

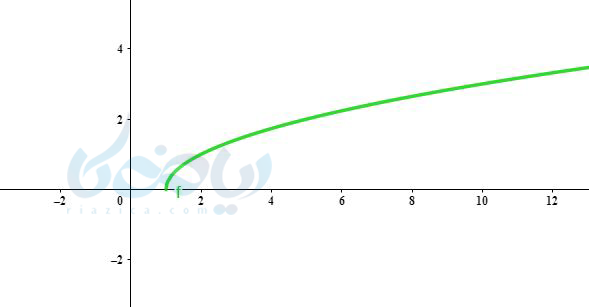
جواب ۳ به روش انتقال:

چون \( \Large x-1 \) شده و \( \Large k<0 \) است پس نمودار یک واحد به سمت راست منتقل می‌شود.

 

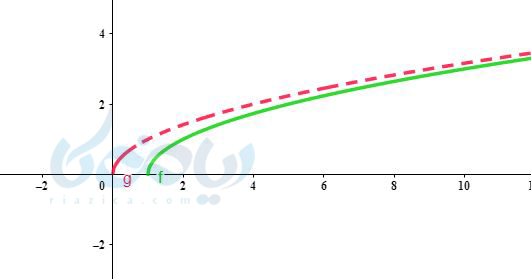
مثال ۴ رسم تابع رادیکالی: نمودار تابع \( \Large y=\sqrt{x} + 2 \) را رسم کنید.

جواب ۴ به روش نقطه یابی:

 

\( \LARGE y=\sqrt{x} + 2 \)

دامنه این تابع برابر است با:

\( \LARGE x \geq 0 \)

\( \LARGE D_f=[0,+\infty ) \)

\( \LARGE R_f=[2,+\infty) \)

\( \LARGE 4 \)	\( \LARGE 1 \)	\( \LARGE 0 \)	x
\( \LARGE 4 \)	\( \LARGE 3 \)	\( \LARGE 2 \)	y

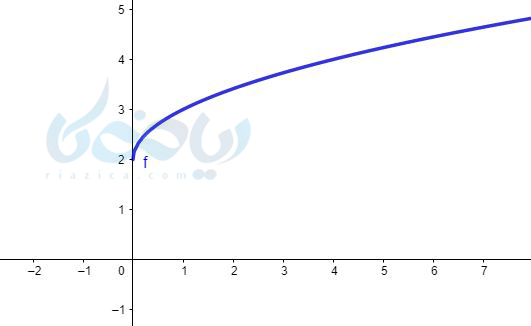
جواب ۴ به روش انتقال:

همانطور که می‌بینید نمودار این تابع رادیکالی دو واحد به سمت بالا منتقل شده است.

به طور کلی:

نمودار \( \Large y=f(x)+k \) در مقایسه با نمودار \( \Large y=f(x) \) اگر \( \Large k>0 \) باشد به اندازه \( \Large k \) روی محور \( \Large y \)ها به سمت بالا منتقل می‌شود و اگر \( \Large k<0 \) باشد به اندازه روی محور \( \Large y \)ها به پایین منتقل می‌شود (انتقال عمودی). یعنی داریم:

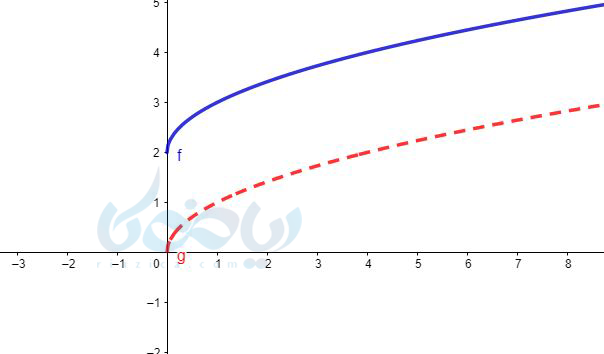
مثال ۵ رسم تابع رادیکالی: نمودار تابع رادیکالی \( \Large y=\sqrt{x-2} +3 \) را رسم کنید.

جواب ۵ به روش نقطه یابی:

\( \LARGE y=\sqrt{x-2} + 3 \)

دامنه این تابع برابر است با:

\( \LARGE x-2 \geq 0 \)

\( \LARGE x \geq 2 \)

\( \LARGE D_f=[2,+\infty ) \)

\( \LARGE R_f=[3,+\infty) \)

\( \LARGE 6 \)	\( \LARGE 3 \)	\( \LARGE 2 \)	x
\( \LARGE 5 \)	\( \LARGE 4 \)	\( \LARGE 3 \)	y

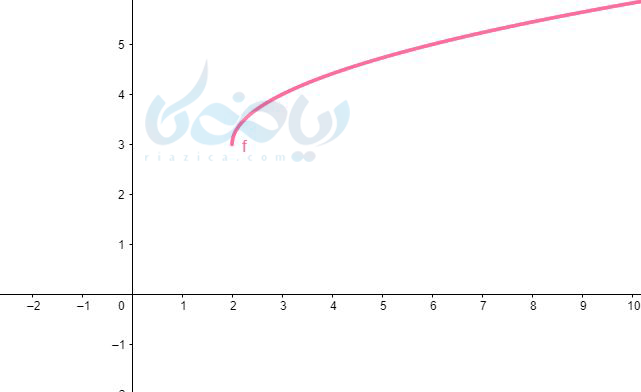
جواب ۵ به روش انتقال:

به روش انتقال نمودار تابع رادیکالی \( \Large y=\sqrt{x}\) را دو واحد به سمت راست و سه واحد به بالا منتقل می‌کنیم.

 

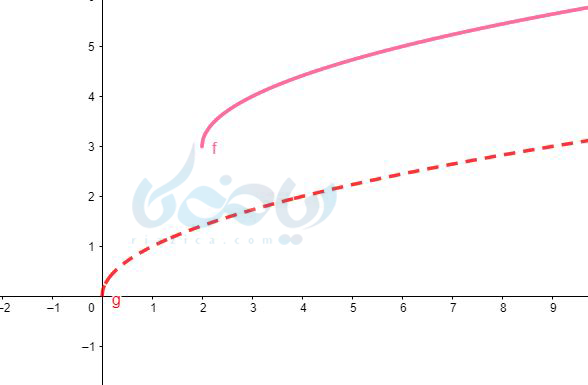
مثال ۶ رسم تابع رادیکالی: نمودار \( \Large y=-\sqrt{x} \) را رسم کنید.

جواب ۶ به روش نقطه یابی:

 

\( \LARGE y=-\sqrt{x} \)

دامنه این تابع برابر است با:

\( \LARGE x \geq 0 \)

\( \LARGE D_f=[0,+\infty ) \)

\( \LARGE R_f=[0,-\infty) \)

\( \LARGE 4 \)	\( \LARGE 1 \)	\( \LARGE 0 \)	x
\( \LARGE -2 \)	\( \LARGE -1 \)	\( \LARGE 0 \)	y

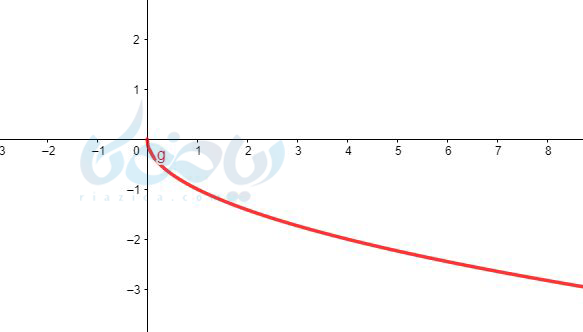
همانطور که می‌بینید نمودار تابع \( \Large y=-\sqrt{x}\) قرینه تابع \( \Large y=\sqrt{x}\) نسبت به محور \( \Large x \)ها می‌باشد.

به طور کلی داریم:

نمودار توابع \( \Large y=f(x) \) و \( \Large y=-f(x) \) قرینه یکدیگرند نسبت به محور \( \Large x \)ها می‌باشند.

مثال ۷ رسم تابع رادیکالی: نمودار تابع \( \Large y=-\sqrt{x-1}+2 \) رسم کنید.

جواب ۷ به روش نقطه یابی:

 

\( \LARGE y=-\sqrt{x-1}+2 \)

دامنه این تابع برابر است با:

\( \LARGE x-1 \geq 0 \)

\( \LARGE x \geq 0 \)

\( \LARGE D_f=[1,+\infty ) \)

\( \LARGE R_f=[2,-\infty) \)

\( \LARGE 5 \)	\( \LARGE 2 \)	\( \LARGE 1 \)	x
\( \LARGE 0 \)	\( \LARGE 1 \)	\( \LARGE 2 \)	y

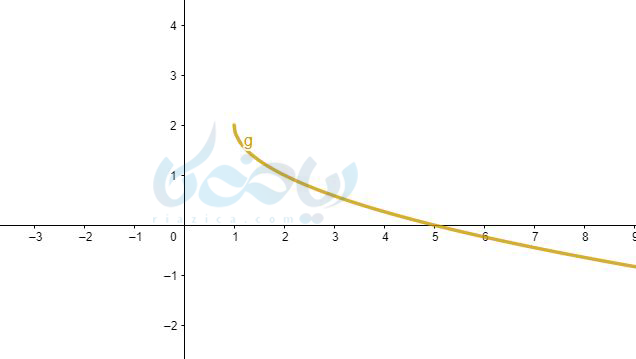
روش انتقال باید نمودار تابع \( \Large y=-\sqrt{x} \) را یک واحد به راست و دو واحد به بالا منتقل کنیم.

جواب ۷ به روش انتقال:

---

---

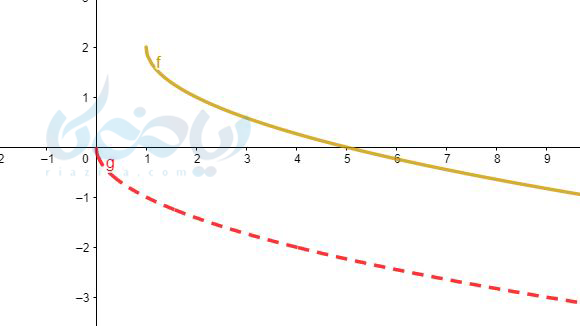
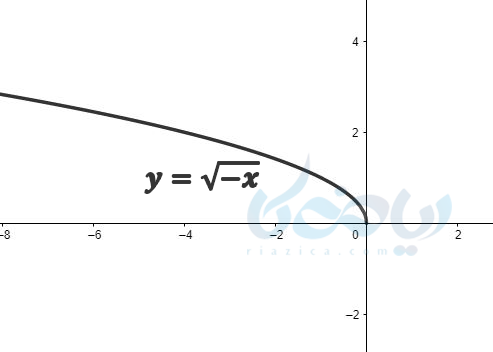
مثال ۸ رسم تابع رادیکالی: نمودار تابع \( \Large y=\sqrt{-x} \) را رسم کنید.

جواب ۸ به روش نقطه یابی:

 

\( \LARGE y=\sqrt{-x} \)

دامنه این تابع برابر است با:

\( \LARGE -x \geq 0 \)

\( \LARGE x \leq 0 \)

\( \LARGE D_f=(-\infty,0] \)

\( \LARGE R_f=[0,+\infty) \)

\( \LARGE -4 \)	\( \LARGE -1 \)	\( \LARGE 0 \)	x
\( \LARGE 2 \)	\( \LARGE 1 \)	\( \LARGE 0 \)	y

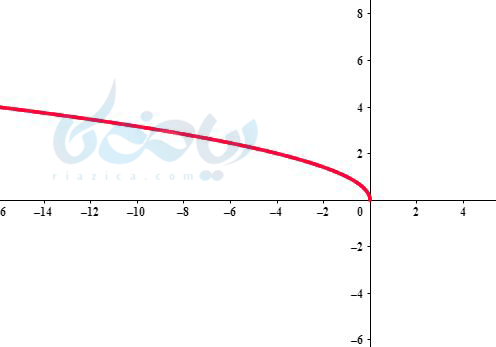
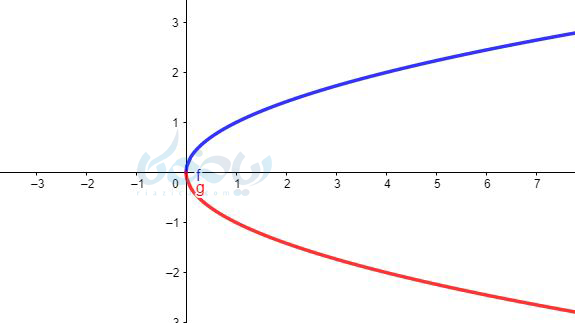
همانطور که می‌بینید نمودار \( \Large y=\sqrt{x} \) و \( \Large y=\sqrt{-x} \) قرینه یکدیگرند نسبت به محور ‌\( \Large y \)ها هستند و به طورکلی:

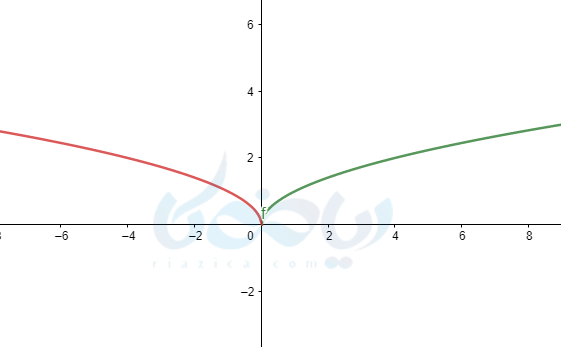
نمودار توابع \( \Large y=f(x) \) و  \( \Large y=f(-x) \)که در آن‌ها تابع فرد است. (یعنی این دو تابع با هم برابر نیستند) نسبت به محور \( \Large y \)ها قرینه یکدیگرند.

 

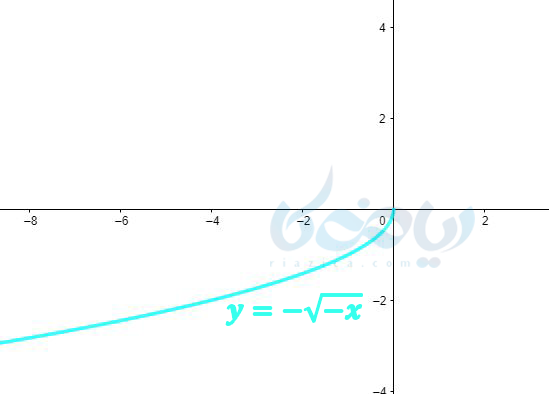
همانطور که در زیر می‌بینید نمودار های \( \Large y=\sqrt{-x} \) و \( \Large y=-\sqrt{-x} \)  نیز نسبت به محور ‌\( \Large x \) ها قرینه یکدیگرند.

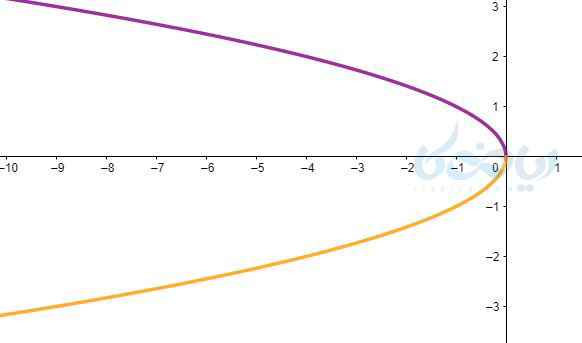
مثال ۹ رسم تابع رادیکالی: نمودار تابع \( \Large y=\sqrt{1-x} \) را رسم کنید.

جواب ۹ به روش نقطه یابی:

\( \LARGE y=\sqrt{1-x} \)

دامنه این تابع برابر است با:

\( \LARGE 1-x \geq 0 \)

\( \LARGE x \leq 1 \)

\( \LARGE D_f=(-\infty,1] \)

\( \LARGE R_f=[0,+\infty) \)

\( \LARGE -3 \)	\( \LARGE 0 \)	\( \LARGE 1 \)	x
\( \LARGE 2 \)	\( \LARGE 1 \)	\( \LARGE 0 \)	y

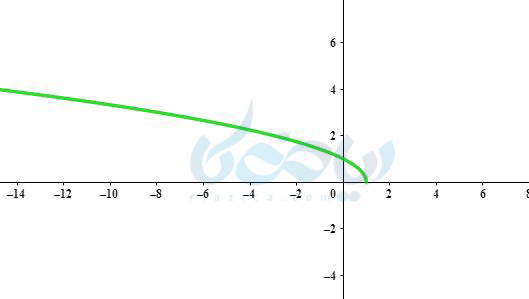
جواب ۹ به روش انتقال:

در واقع \( \Large y=\sqrt{1-x} \) برابر است با \( \Large y=\sqrt{-(x-1)} \) پس باید نمودار \( \Large y=\sqrt{-x} \) یک واحد به سمت راست منتقل کنیم چون \( \Large K<0 \) است.

 

 

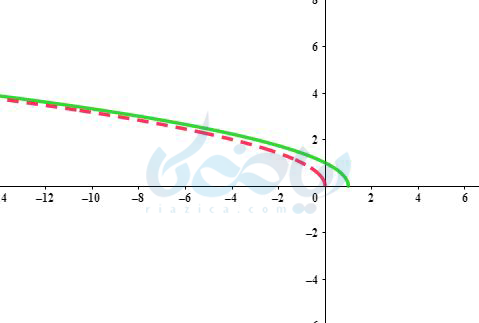
نمودارهای اصلی (مادر) تابع رادیکالی

پس نمودارهای اصلی (مادر) توابع رادیکالی ساده به یکی از چهار صورت زیر هستند که بقیه توابع رادیکالی را می‌توان با انتقال این توابع بدست آورد.

 

 

 

 

 

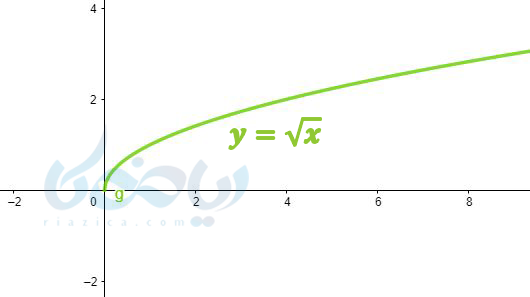
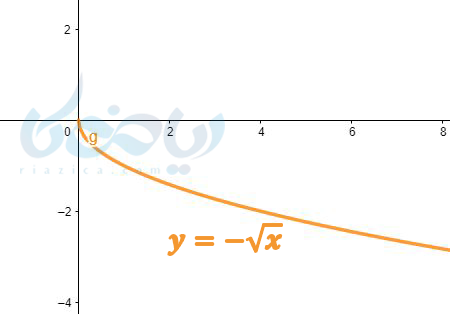
البته ما در این درسنامه ساده‌ترین نمودار تابع رادیکالی را برایتان شرح دادیم. که در کتاب درسی شما وجود دارد. توابع رادیکالی زیادی وجود دارند که به روش‌های دیگر رسم می‌شوند.

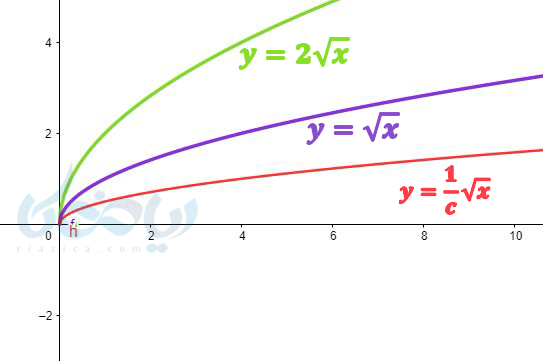
نمودار تابع \( \Large y=a\sqrt{x} \)

نمودار \( \Large y=a\sqrt{x} \) اگر \( \Large \left| a \right| > 1 \) باشد نمودار تابع رادیکالی از محور \( \Large x \)ها دور می‌شود و اگر قدرمطلق \( \Large a \) بین صفر و یک باشد نمودار تابع رادیکالی به محور \( \Large x \)ها ها نزدیک می‌شود.

در ادامه توصیه میشه تابع جز صحیح را مطالعه کنید.

زنگ آخر رسم تابع رادیکالی

خوب رفقا باهم رسم تابع رادیکالی از ریاضی یازدهم تجربی را کامل، کامل یادگرفتیم. دوستان حتما عکس‌های خلاصه را ذخیره کنید و مرورشون کنید. با حل کردن چندتا مثال به راحتی آب خوردن میتونید رو این بحث تسلط کافی پیدا کنید.

هر سوالی از این مبحث داشتید کافیه برامون در قسمت دیدگاه بنویسید. کارشناسان ریاضیکا قطعا بهتون پاسخ می‌دهند.

---

---