واحد های اندازه‌ گیری زاویه 💎💯 – تبدیل درجه و رادیان یادبگیر!

در پست واحد های اندازه‌ گیری زاویه از ریاضی یازدهم تجربی یادمی‌گیرید، در سال‌های گذشته با واحد اندازه گیری درجه برای اندازه گیری زاویه آشنا شده‌اید و از نقاله برای رسم زاویه با اندازه مورد نظر استفاده کرده‌اید حال می‌خواهیم در این درسنامه شما را با یک واحد دیگر به نام رادیان آشنا کنیم و چگونگی تبدیل رادیان به درجه و برعکس را آموزش دهیم. البته لازم به ذکر است که واحد اندازه گیری دیگری به نام گردا هم برای زاویه وجود دارد که بعدها با آن آشنا خواهید شد.

تعریف زاویه به عنوان یک واحد اندازه گیری زاویه

اگر محیط دایره را به 360 کمان مساوی تقسیم کنیم اندازه زاویه مرکزی روبروی هر کدام از این کمان‌ها 1 درجه می‌باشد. می‌دانیم اندازه هر کمان با اندازه زاویه مرکزی روبروی آن با هم برابرند. وسیله اندازه گیری زاویه نقاله هست که در واقع یک نیم دایره است که به 180 قسمت مساوی تقسیم شده است.

نکته واحد های اندازه‌ گیری زاویه: لازم به توضیح است که بگوییم جنس زاویه از جنس دوران است که ما آن را در درسنامه مثلثات توضیح داده‌ایم.

دایره مثلثاتی رانیز در درسنامه دایره مثلثاتی به طور کامل تعریف کرده‌ایم. حال باز یه طور مختصر آن را تعریف می‌کنیم.

تعریف دایره مثلثاتی

دایره مثلثاتی دایره‌ای است به شعاع واحد که جهت دوران در آن خلاف عقربه‌های ساعت است و محورهای مختصات قطرهای آن می‌باشند و مبدا آن نیز محل برخورد دایره با جهت مثبت محور \( \Large x \) ها می‌باشد.

تعریف رادیان در واحد های اندازه‌ گیری زاویه

اگر روی محیط یک دایره به شعاع \( \Large r \) به اندازه شعاع ،کمانی را جدا کنیم زاویه مرکزی روبروی آن 1 رادیان نام دارد.

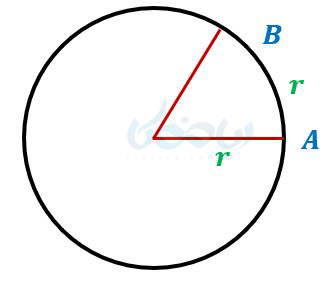
برای درک بهتره دایره ای به شعاع \( \Large r \) در نظربگیرید دهانه پرگار را به اندازه \( \Large r \) باز کرده و وسوزن پرگار را روی نقطه \( \Large A \) بگذارید و یک کمان بزنید تا دایره را در نقطه \( \Large B \) قطع کند زاویه مرکزی \( \Large AOB \) یک رادیان می‌باشد که تقریبا \(\Large  57.3 ^{\circ} \) خواهد بود.

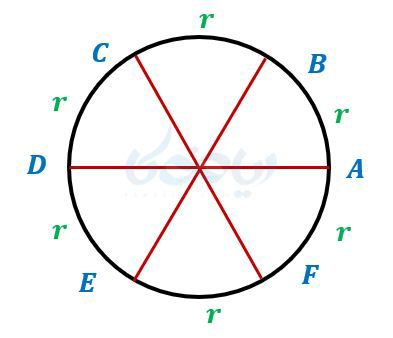
اگر این کار را ادامه دهید می‌بینید 6 زاویه مرکزی که طول کمان روبروی آن‌ها با شعاع برابر است به وجود می‌آید که هر کدام آن‌ها یک رادیان است. پس داریم:

1 رادیان برابر است با اندازه زاویه مرکزی دایره‌ای که طول کمان روبروی آن با شعاع دایره مساوی است.

پس به این ترتیب خواهیم داشت:

مثال ۱ واحد های اندازه‌ گیری زاویه: یک دو چرخه سوار در یک پیست دوچرخه سواری به شعاع ۲۰ متر رکاب می‌زند اگر این دوچرخه سوار ۵۰۰ متر رکاب بزند چند رادیان دوران کرده؟

حل ۱:

\(\LARGE  \alpha =\frac{l}{r} \)

\(\LARGE  \alpha =\frac{500}{20}=25 rad \)

تبدیل رادیان به درجه و بالعکس

می‌داینم عدد پی برابر است با نسبت محیط دایره به قطر آن:

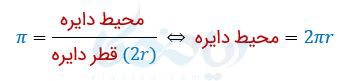
که مقدار تقریبی آن \(\Large  \pi \simeq 3.14 \) می‌باشد. پس نصف محیط دایره \(\Large  \pi r \) می‌باشد در نتیجه زاویه مرکزی روبروی یک نیم دایره برحسب رادیان برابر است با:

\(\LARGE \alpha = \frac{\pi r}{r} = \pi   \)

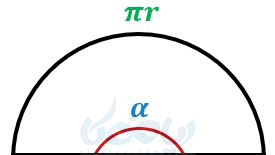
از طرفی می‌دانیم این زاویه بر حسب درجه ۱۸۰ می‌باشد. پس یک درجه برابر است با \(\Large \frac{\pi}{180} \) رادیان. یعنی برای تبدیل درجه به رادیان کافی است آن را در \(\Large \frac{\pi}{180} \) رادیان ضرب کنیم.

\(\LARGE 30 ^{\circ}  \rightarrow \frac{\pi}{6}  rad \)

\(\LARGE 45 ^{\circ}  \rightarrow \frac{\pi}{4}  rad \)

\(\LARGE 60 ^{\circ}  \rightarrow \frac{\pi}{3}  rad \)

\(\LARGE 90 ^{\circ}  \rightarrow \frac{\pi}{2}  rad \)

\(\LARGE 120 ^{\circ}  \rightarrow \frac{2\pi}{3}  rad \)

\(\LARGE 150 ^{\circ}  \rightarrow \frac{5\pi}{6}  rad \)

و برعکس برای تبدیل رادیان به درجه بر \(\Large \frac{\pi}{180} \) تقسیم می‌کنیم. و با توجه به اینکه در تقسیم اعداد گویا تقسیم به ضرب تبدیل شده و کسر دوم معکوس می‌شود. پس کافیست در \(\Large \frac{180}{\pi} \) ضرب کنیم. پس داریم:

\(\LARGE 1 rad \rightarrow 57.3 ^{\circ} \)

\(\LARGE \frac{\pi}{36} rad \rightarrow 5^{\circ} \)

\(\LARGE \frac{2\pi}{5} rad \rightarrow 72 ^{\circ} \)

\(\LARGE \frac{5\pi}{4} rad \rightarrow 225 ^{\circ} \)

اگر \(\Large D \) اندازه زاویه \(\Large  \alpha \) بر حسب درجه و \(\Large  R \) اندازه زاویه \(\Large  \alpha \) بر حسب رادیان باشد:

\(\LARGE  \frac{D}{180}=\frac{R}{\pi} \)

نکته واحد های اندازه‌ گیری زاویه: می‌توان گفت رادیان واحدی برای تبدیل دوران به طول است.

مثال ۲ واحد های اندازه‌ گیری زاویه: یک دونده در یک زمین دو میدانی دایره شکل به شعاع ۵۰ متر در حال دویدن است اگر او ۳۱۵ درجه دوران کند چند متر دویده است؟

حل ۲: ابتدا واحد درجه را به رادیان تبدیل می‌کنیم.

\(\LARGE  315 \times \frac{\pi}{180} = \frac{7\pi}{4} \)

\(\LARGE  \alpha = \frac{7\pi}{4} rad  \)

\(\LARGE r=50 m  \)

\(\LARGE  \alpha = \frac{l}{r} \)

\(\LARGE \frac{7\pi}{4} = \frac{l}{50} \)

\(\LARGE l = \frac{350\pi}{4} \simeq 274.75 m \)

ویدیو از واحدهای اندازه گیری زاویه

در این گیفت جالب رابطه درجه ورادیان رو مشاهده می کنید.

زنگ آخر واحد های اندازه‌ گیری زاویه

خوب رفقا باهم واحد های اندازه‌ گیری زاویه  از ریاضی یازدهم تجربی را کامل، کامل یادگرفتیم. با مفهوم درجه و رادیان آشنا شدیم و نحوه تبدیل آن‌ها را نیز به یکدیگر فراگرفتیم. هر سوالی از این مبحث داشتید کافیه برامون در قسمت دیدگاه بنویسید. کارشناسان ریاضیکا قطعا بهتون پاسخ می‌دهند.