آموزش ریاضی پایه یازدهم تجربی
تابع جز صحیح 🈁✅ – به زیر دستت نگاه کن!
یکی از توابع زیبا که نمودار آن نیز نموداری زیبا و متنوع است و کاربردهای زیادی در ریاضیات دارد تابع جزء صحیح میباشد ما در این پست میخواهیم مفهوم جزء صحیح و پیدا کردن جزء صحیح یک عدد و خواص آن را به شما آموزش دهیم سپس تابع جزء صحیح را فرض کرده و چگونگی رسم نمودار آن را نیز به شما بیاموزیم پس همراه ما باشید.
مثالی از تابع جزء صحیح
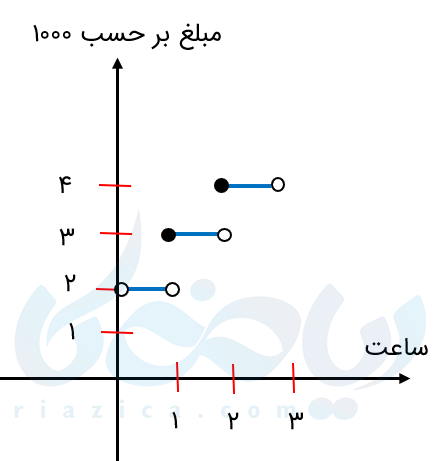
حتما شما یا خانوادهتان وقتی به مراکز خرید یا مکانهای دیگر میروید و اتومبیل خود را در پارکینگها پارک میکنید دیدهاید که نرخ پارکینگها در بازههای زمانی مختلف تغییر میکند مثلا از وقتی وارد میشود تا زیر یک ساعت یک مبلغی به عنوان ورودی از شما دریافت میکنند فرض کنید ۲۰۰۰ تومان از یک ساعت تا دو ساعت ۳۰۰۰ تومان از دو ساعت تا سه ساعت ۴۰۰۰ تومان و الی آخر.
| مبلغ | زمان |
|---|---|
| ۲۰۰۰ تومان | از زمان ورود تا زیر یک ساعت |
| ۳۰۰۰ تومان | از یک ساعت تا دو ساعت |
| ۴۰۰۰ تومان | از دو ساعت تا سه ساعت |
جزء صحیح یک عدد
هر عدد حقیقی را میتوان به صورت جمع یک عدد صحیح و یک عدد اعشاری نوشت. به مثالهای زیر دقت کنید:
\( \LARGE 3.14=3+0.14 \)
\( \LARGE 125.012=125+0.012 \)
\( \LARGE \Pi = 3.14….. \)
\( \LARGE = 3 + 0.14….. \)
\( \LARGE \sqrt{2}=1.141….=1+0.14 \)
دقت کنید که جزء صحیح اعداد از آنها کوچکتر است و در واقع اولین عدد صحیح سمت چپ آن عدد حقیقی میباشد.
که نماد جزء صحیح براکت \( \Large [\;] \) میباشد که توسط ریاضیدان بزرگ گاوس در سال ۱۸۰۸ میلادی انتخاب شد البته امروزه از نماد \( \Large \lfloor \rfloor \) یا \( \Large \lceil \rceil \) نیز استفاده میشود. پس داریم:
\( \LARGE [3.14] =3 \)
\( \LARGE [125] =125 \)
\( \LARGE [\Pi] =3 \)
\( \LARGE [\sqrt{2}] =1 \)
پس در مورد اعداد منفی نیز جزء صحیح اولین عدد سمت چپ آنها میباشد. یعنی داریم:
\( \LARGE [-1.2] =-2 \)
\( \LARGE [-0.5] =-1 \)
\( \LARGE [-\Pi] =-4 \)
اما تعریف دقیق جزء صحیح اعداد به صورت زیر میباشد.
جز صحیح هر عدد حقیقی
جزء صحیح هر عدد حقیقی بزرگترین عدد صحیح کوچکتر از آن عدد میباشد که با نماد براکت \( \Large ([\;]) \) نمایش داده میشود.
به زبان دیگر: اگر \( \Large n \) یک عدد صحیح و \( \Large x \) یک عدد حقیقی باشد به طوریکه:
\( \LARGE n \leq x < n+1 \Leftrightarrow [x]=n \)
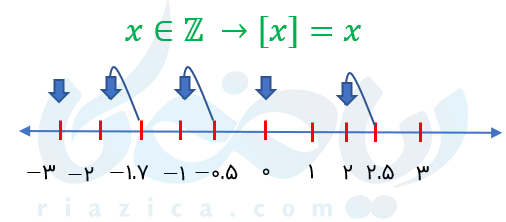
نکته: بنابر تعریف، جزء صحیح اعداد صحیح برابر خودشان میباشد.
یعنی:
مثال:
(1
\( \LARGE [3.14]=3 \Leftrightarrow 3 \leq 3.14 <4 \)
(2
\( \LARGE [5]=5 \Leftrightarrow 5 \leq 5 <6 \)
(3
\( \LARGE [0]=0 \Leftrightarrow 0 \leq 0 <1 \)
(4
\( \LARGE [-\sqrt3]=-2 \Leftrightarrow -2 \leq -\sqrt3 <-1 \)
(5
\( \LARGE [-\frac{1}{5}]=-1 \Leftrightarrow -1 \leq -\frac{1}{5} <۰ \)
(6
\( \LARGE [\frac{7}{2}]=3 \Leftrightarrow 3 \leq \frac{7}{2} <4 \)
(7
\( \LARGE [sin30]=0 \Leftrightarrow 0 \leq sin30 <1 \)
(8
\( \LARGE [cos120]=-1 \)
\( \LARGE \Leftrightarrow -1 \leq cos120 <0 \)
(9
\( \LARGE [\frac{3}{4}]=۰ \Leftrightarrow 0 \leq \frac{3}{4} <1 \)
(10
\( \LARGE [log_2 2^4]=4 \)
\( \LARGE log_2 2^4 \leq log_2 2^4 <log_2 2^5 \)
\( \LARGE 4 \leq log_2 2^4 <5 \)
خواص جزء صحیح

تابع جزء صحیح
تابع جزء صحیح تابعی است که به هر عدد صحیح خود همان عدد صحیح را نسبت میدهد و به هر عدد غیر صحیح، بزرگترین عدد صحیح کوچکتر از آن را نسبت میدهد و ضابطه آن \( \Large f{(x)}=[x] \) یا \( \Large y=[x] \) نشان داده میشود.
معادلات تابع جزء صحیح
وقتی معادله شامل براکت (جزء صحیح) داریم از تعریف تابع جزء صحیح و خواص جزء صحیح و تنها کردن براکت آن را حل میکنیم به مثالهای زیر دقت کنید.
مثال ۱: معادله زیر را حل کنید.
\( \LARGE [x]=5 \)
جواب ۱:
همانطور که میبینید در این معادله ساده ما یک دسته جواب داریم یعنی تمام اعداد بین ۵ و ۶ و خود ۵ میتواند جزء صحیح شان ۵ باشد.
\( \LARGE [x]=5 \rightarrow 5 \leq x < 6 \)
مجموعه جواب:
\( \LARGE [5,6) \)
مثال ۲: معادله زیر را حل کنید.
\( \LARGE [x+3]-7=2 \)
جواب ۲:
\( \LARGE [x]+3=9 \)
\( \LARGE [x]=6 \)
\( \LARGE 6 \leq x < 7 \)
مجموعه جواب:
\( \LARGE [6,7) \)
مثال ۳: معادله زیر را حل کنید.
\( \LARGE [2x+3]=2 \)
جواب ۳:
\( \LARGE [2x]+3=2 \)
\( \LARGE [2x]=-1 \)
\( \LARGE -1 \leq 2x < 0 \)
\( \LARGE -\frac{1}{2} \leq x < 0 \)
مجموعه جواب:
\( \LARGE [-\frac{1}{2},0) \)
مثال ۴: معادله زیر را حل کنید.
\( \LARGE 2[x]+[x-1]=2 \)
جواب ۴:
\( \LARGE 2[x]+[x] -1=2 \)
\( \LARGE 3[x]=3 \)
\( \LARGE [x]=1 \)
\( \LARGE 1 \leq x < 2 \)
مجموعه جواب:
\( \LARGE [1,2) \)
مثال ۵: معادله زیر را حل کنید.
\( \LARGE [\frac{1-3x}{4}]=4 \)
جواب ۵:
\( \LARGE 4 \leq \frac{1-3x}{4} < 5 \)
طرفین را ضربدر ۴ میکنیم :
\( \LARGE 16 \leq 1-3x <20 \)
طرفین را منهای ۱ میکنیم:
\( \LARGE 15 \leq -3x <19 \)
طرفین را تقسیم بر ۳- میکنیم:
\( \LARGE -5 \geq x > -\frac{19}{3} \)
مجموعه جواب:
\( \LARGE (-\frac{19}{3},-5] \)
مثال ۶: معادله زیر را حل کنید.
\( \LARGE 2[3x-2]=1 \)
جواب ۶:
\( \LARGE [3x-2]=\frac{1}{2} \)
معادله جواب ندارد چون:
\( \LARGE [u]=K \rightarrow K \in \mathbb{Z} \)
همیشه باید جواب براکت یک عدد صحیح باشد پس این معادله جواب ندارد.
مثال ۷: مجموعه جواب معادله زیر را بدست آورید.
\( \LARGE [x]^2-3[x]-10=0 \)
جواب ۷:
برای حل ایم معادله از تغییر متغیر استفاده میکنیم:
\( \LARGE [x]=t \rightarrow [x]^2=t^2 \)
\( \LARGE t^2-3t-10=0 \)
\( \LARGE (t-5)(t+2)=0 \)
\( \LARGE t=5,t=-2 \)
\( \LARGE [x]=5 \rightarrow 5 \leq x <6 \)
\( \LARGE [x]=-2 \rightarrow -2 \leq x <-1 \)
مجموعه جواب:
\( \LARGE [5,6) \cup [-2,-1) \)
در ادامه پست رسم تابع جزء صحیح را مطالعه کنید.
زنگ آخر تابع جزء صحیح
در این نوشتار مبحث تابع جزء صحیح از ریاضی یازدهم تجربی را به طور کامل یادگرفتیم. حتما سعی کنید تعریف و مفهوم کلی این تابع را درک کنید. هر سوالی از تابع جزء صحیح داشتید در قسمت دیدگاه از ما بپرسید دوستان ریاضیکا حتما به سوالاتتان پاسخ میدهند. موفق باشید.





سلام درمورد رسم این توابع هم توضیح بدید ممنون
سلام و عرض ادب
به پست زیر مراجعه کنید:
https://riazica.com/draw-floor-and-ceiling-functions/
موفق باشید.
عرض سلامووقت بخیرببخشیدنمودارایکس درجزصحیح ایکس چطور رسم میشه؟
سلام دوست عزیز
به پستhttps://riazica.com/draw-floor-and-ceiling-functions/ مراجع کن
براکت پی +براکت رادیکال پی چند می شود؟
با سلام دوست عزیز
براکت عدد پی میشود سه وبراکت رادیکال پی میشود یک پس مجموعشان میشود چهار
سلام
لطفا تابع براکت یازدهم انسانی هم بگید
سلام و عرض ادب
فرق زیادی ندارد، در آینده هم قرار میدهیم.
موفق باشید
سلام میشه راجب براکت اعداد منفی هم توضیح بدین وقتی متغیر به منفی یا مثبت از سمت چپ یا راست میل میکنه …. و همینطور همین حالت وقتی که متغیر داخل براکت ضریب داره …. ممنونم
سلام وعرض ادب
به زودی در ادامه پست گذاشته خواهد شد توصیه میشه پست رسم نمودار جزصحیح هم مطالعه بشه
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام
https://riazica.com/draw-floor-and-ceiling-functions/ این پست رو هم بخونید
در قسمت شماره ۱ خواص جزء صحیح داریم کوچکتر و مساوی n+1 . فکر میکنم علامت مساوی اضافه باشه.
با سلام وعرض ادب
ممنون از دقت نظر شما اصلاح میشود
سلام می تونید یک تعریف کلی درمورد تابع جزئه صحیح بدید
با سلام وعرض ادب
جز صحیح عدد صحیح خودش مبشود وجز صیحیح اعداد غیر صحیح میشود اولین عدد صحیح قبل از خودش مثلا جز صحیح عدد ۲/۵ میشود ۲ چون بین دوعدد صحیح ۲و۳ هست
سلام وقتتون بخیر
ببخشید میشه جواب براکت زیر رو برام بگید ممنون میشم 9=[3+[x]]
با سلام وادب
میشه ایکس بین بزگتر یا مساوی شش وکوچکتر از هفت
با سلام جزء صحیح عدد رادیکال پنج چند میشود
با سلام
میشه ۲
سلام یه سوال داشتم حد جز صحیح [x-]-lim x ایکس میل می کند به ۳ ازسمت چپ چطوری حل میشه؟
سلام
این چطوری حل میشه؟
0=10+[x] 5؟
سلام
ابتدا مثل یه معادله ساده حلش کنید تا براکت ایکس تنها بشه یعنی ده رو ببرید اونطرف وبه پنج تقسیم کنید جواب میشه منفی دو حالا ببینید درچه بازه ای جواب براکت میشه منفی دو
درسته در بازه نیم باز منفی یک تا منفی دو بسته
سپاسگزارم
با سلام وادب
ممنون از لطف شما
سلام
این چطوری حل میشه؟
0=10+[x] 5؟
سلام جسارتا توی خواص جز صحیح خط چهار یک اشتباهی رخ داده و کوچک تر مساوی گذاشته شده
با سلام وادب ممنون از دقت نظر شما اصلاح میشود
اصلاح شد
سلام
می خواستم درمورد این متن برام توضیح بدین
برای هر عدد حقیقی k، داریم [x+k]=[x]+k
با سلام اگه k عدد غیر صحیح باشه درست نیست
سلام
می خواستم درمورد این متن برام توضیح بدین
برای هر عدد حقیقی k، داریم [x+k]=[x]+k
جملات یکم جابه جا شدن
آیا این درسته؟؟
یا سلام وادب
اگه k عدد صحیح باشه درسته