آموزش ریاضی پایه دوازدهم تجربی
تبدیل نمودار توابع 👣📉 – گام به گام با تصویر!
شهریور
در این درسنامه به مبحث تبدیل نمودار توابع دوازدهم تجربی میپردازیم. در حل بسیاری از مسائل فصول مختلف کتاب، نیاز به تسلط کافی روی این مبحث دارید. بنابراین توصیه میکنیم تا با جدیت بیشتری این مبحث را دنبال کنید. به طور کلی در این درسنامه به دنبال آن هستیم تا با دانستن نمودار تابع \(\Large f(x)\)، نمودار توابع \(\Large f(kx)\)، \(\Large kf(x)\) و \(\Large |f(x)|\) را که \(\Large k\) یک عدد دلخواه است، رسم کنیم.
نمودار \(\Large kf(x)\)
در مورد تابع \(\Large y=kf(x)\) میخواهیم سه مورد را بررسی کنیم. اول از همه اینکه نمودار آن چه ارتباطی با نمودار \(\Large f\) دارد و به ازای چه مقادیری از \(\Large k\)، نمودار دچار انقباض یا انبساط میشود. بعد از این، دامنه و برد آن را بررسی میکنیم. در آخر نیز به بررسی نقاط تقاطع آن با محور \(\Large x\)ها که همان ریشههای معادلۀ \(\Large kf(x)=0\) است، میپردازیم.
انقباض و انبساط
همانطور که در پایۀ یازدهم خواندید، برای رسم نمودار تابع با ضابطۀ \(\Large kf(x)\) با استفاده از روش تبدیل نمودار توابع باید عرض هر نقطه از نمودار تابع \(\Large f(x)\) را \(\Large k\) برابر کنیم. بسته به مقدار \(\Large k\)، نمودار تابع یا دچار انقباض یا انبساط عمودی میشود، یا ابتدا قرینه شده و سپس دچار انقباض و انبساط عمودی میگردد. برای اینکه بهتر متوجه شوید، نمودار تابع \(\Large f(x)\) که در شکل زیر رسم شده است را در نظر بگیرید.
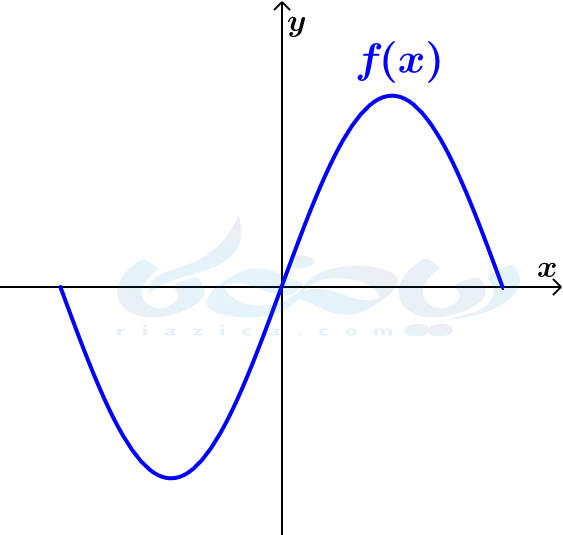
به طور کلی سه حالت رخ میدهد:
- \(\Large k\) عددی بین \(\Large 0\) و \(\Large 1\) است. در این حالت، نمودار تابع \(\Large y=kf(x)\) از انقباض عمودی نمودار \(\Large f\) به دست آمده و به شکل زیر خواهد شد:
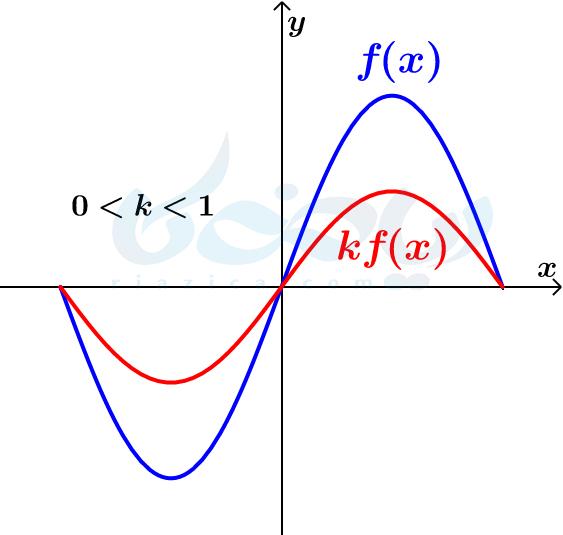
- \(\Large k\) عددی بزرگتر از \(\Large 1\) است. در این حالت، نمودار تابع \(\Large y=kf(x)\) از انبساط عمودی نمودار تابع \(\Large f(x)\) به دست آمده و به شکل زیر خواهد شد:
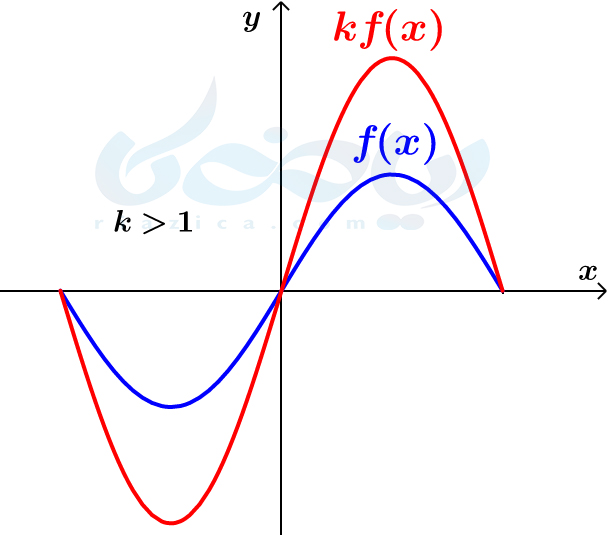
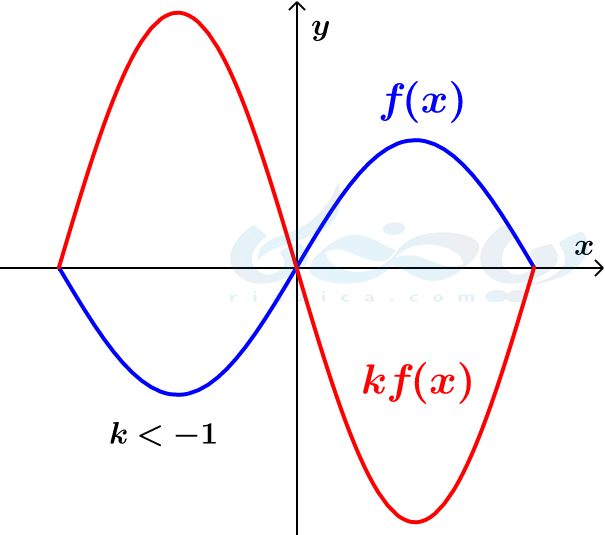
- \(\Large k\) عددی منفی است. در این حالت، ابتدا نمودار تابع \(\Large f(x)\) را نسبت به محور \(\Large x\)ها قرینه میکنیم، اگر \(\Large k\) بین \(\Large 0\) و \(\Large -1\) باشد، نمودار را منقبض و اگر \(\Large k\) کوچکتر از \(\Large -1\) باشد، نمودار را منبسط میکنیم. نمودار هر دو حالت در دو شکل زیر رسم شده است.
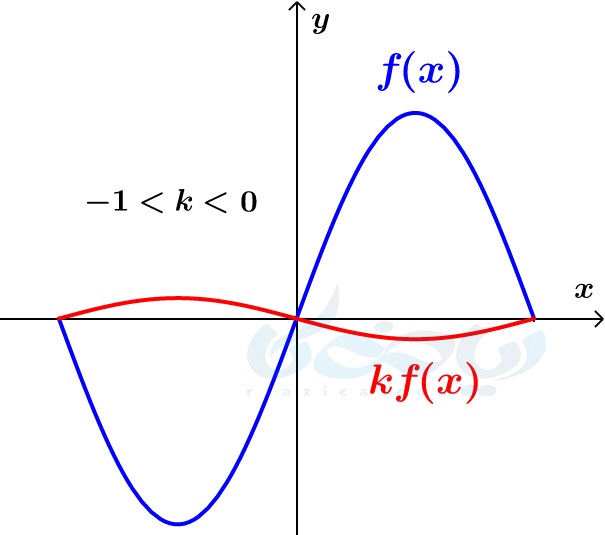
ریشهها
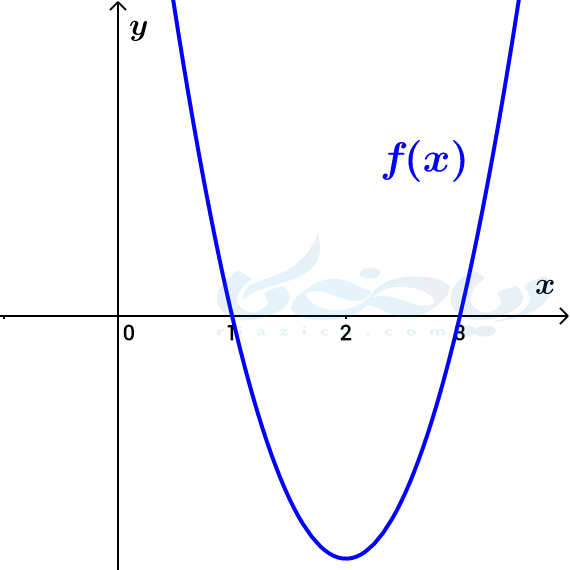
تابع \(\Large f(x)\) را در نظر بگیرید. اگر به ازای \(\Large x_0\) داشته باشیم \(\Large f(x_0)=0\)، میگوییم \(\Large x_0\) ریشۀ معادلۀ \(\Large f(x)=0\) است. همچنین، نقطۀ \(\Large (x_0, 0)\) روی نمودار تابع \(\Large f(x)\) بوده و به عبارتی دیگر، تابع \(\Large f(x)\)، محور \(\Large x\)ها را در نقطۀ \(\Large x_0\) قطع میکند. مثلاً، در شکل زیر، \(\Large x=3\) و \(\Large x=1\) ریشههای معادلۀ \(\Large f(x)=0\) بوده و نمودار \(\Large f\) محور \(\Large x\)ها را در \(\Large x=3\) و \(\Large x=1\) قطع میکند.
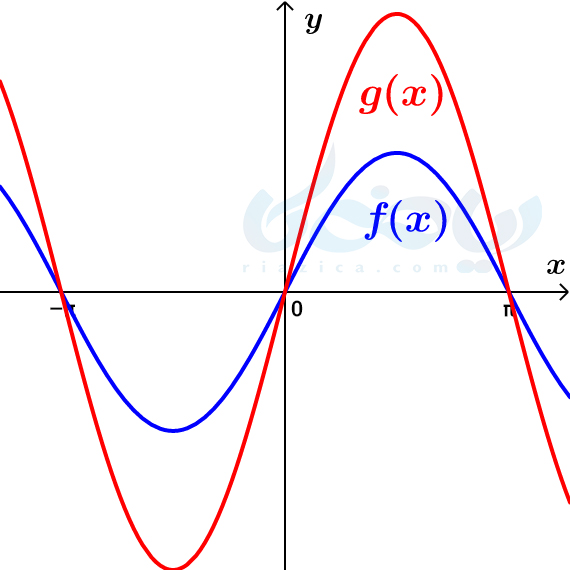
در مورد ریشههای معادلۀ \(\Large kf(x)=0\) چه میتوانیم بگوییم؟ طبیعتاً هر \(\Large x\) که \(\Large f(x)\) را صفر کند، \(\Large kf(x)\) را نیز صفر خواهد کرد. پس، ریشههای معادلۀ \(\Large f(x)=0\)، ریشههای معادلۀ \(\Large kf(x)=0\) نیز هست و نقاط تلاقی تابع \(\Large f(x)\) با محور \(\Large x\)ها با تابع \(\Large y=kf(x)\) یکسان است. میتوانید این موضوع را برای نمودار دو تابع \(\Large f(x)=\sin x\) و \(\Large g(x)=2 \sin x\) که در شکل زیر رسم شده است، مشاهده کنید.
دامنه و برد در مبحث تبدیل نمودار توابع
از آنجاییکه با ضرب عدد \(\Large k\) در \(\Large f(x)\)، تغییری در \(\Large x\)ها صورت نمیگیرد، دامنۀ تابع \(\Large f(x)\) و \(\Large y=kf(x)\) یکی است. اما در مورد برد این دو تابع چه میتوان گفت؟ به مثالهای زیر دقت کنید.
مثال 1: در شکل زیر نمودار تابع \(\Large f(x)=\cos (x)\) رسم شده است. نمودار توابع \(\Large g(x)=2 f(x)\) و \(\Large h(x)=-\frac{1}{2}f(x)\) را با استفاده از نمودار تابع \(\Large f(x)\) به دست آورده و برد هر یک را مشخص کنید.
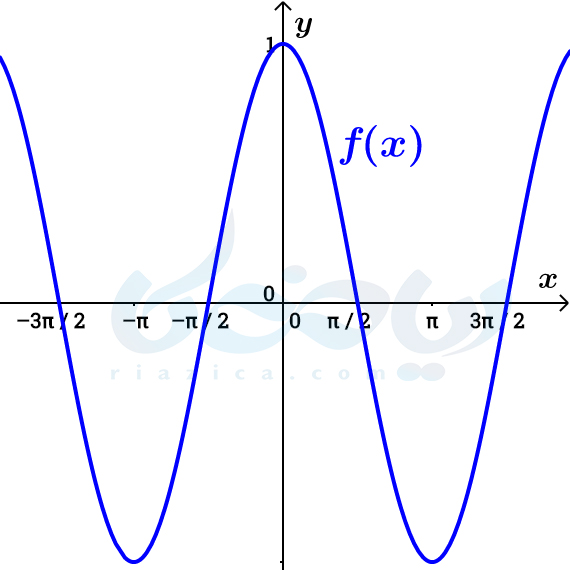
حل: همانطور که گفتیم، نمودار تابع \(\Large g(x)=2 f(x)\) از انبساط عموی \(\Large f\) و نمودار تابع \(\Large h(x)=-\frac{1}{2}f(x)\) از قرینه و سپس انقباض عمودی \(\Large f\) به دست میآید. بنابراین نمودار دو تابع \(\Large g(x)\) و \(\Large h(x)\) به صورت زیر خواهد بود:
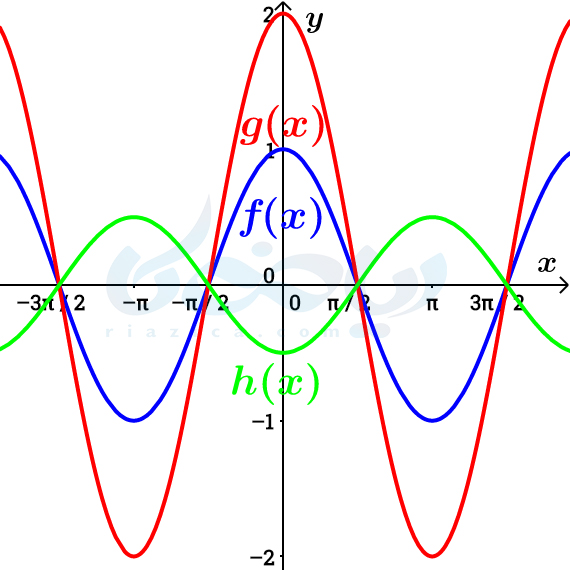
همان طور که میبینیم، برد تابع \(\Large f(x)\) برابر با \(\Large [-1, 1]\)، برد \(\Large g(x)\) برابر با \(\Large [-2, 2]\) و برد \(\Large h(x)\) برابر با \(\Large [\frac{-1}{2}, \frac{1}{2}]\) است.
مثال 2: در شکل زیر نمودار تابع \(\Large f(x)=x\) رسم شده است. نمودار توابع \(\Large g(x)=2f(x)\) و \(\Large h(x)=-\frac{1}{2}f(x)\) را به دست آورده و برد هر یک را مشخص کنید.
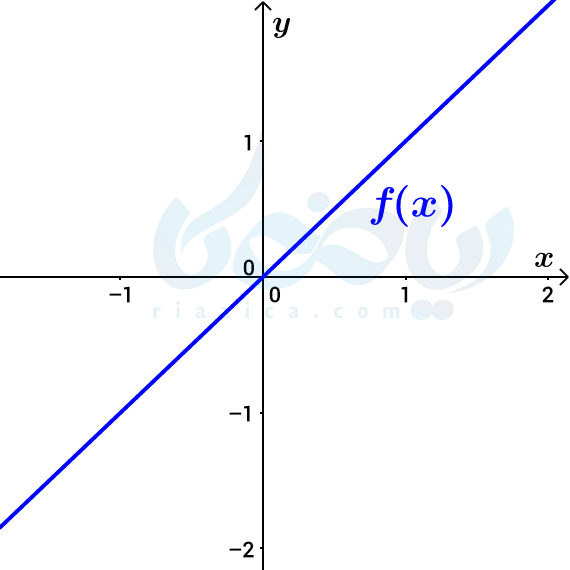
حل: نمودار \(\Large g(x)=2f(x)\) را با انبساط عمودی \(\Large f\) و نمودار تابع \(\Large h(x)=-\frac{1}{2}f(x)\) را با قرینه کردن و انقباض عمودی \(\Large f\) به صورت زیر رسم میکنیم:
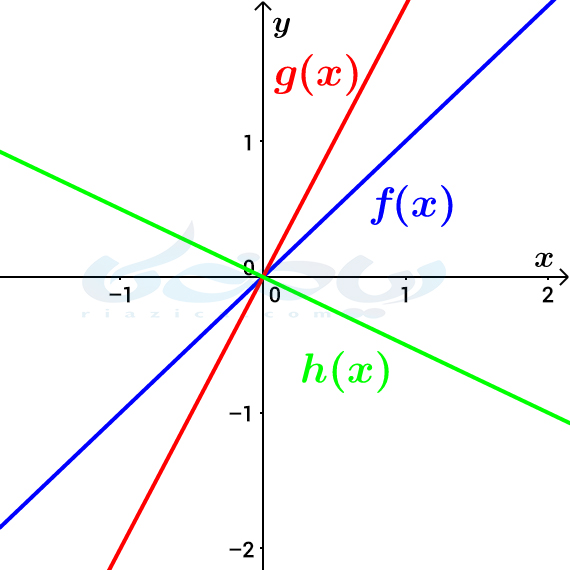
همان طور که میبینید، برد هر سه تابع \(\Large f(x)\) و \(\Large g(x)=2f(x)\) و \(\Large h(x)=-\frac{1}{2}f(x)\) برابر با \(\Large \mathbb{R}\) است.
با توجه به این دو مثال، نمیتوان یک رابطۀ کلی بین برد تابع \(\Large f(x)\) و تابع \(\Large y=kf(x)\) به دست آورد. در مثال 2، برد هر سه تابع برابر بود، اما در مثال 1 این اتفاق رخ نداد.
پیدا کردن برد بدون تبدیل نمودار توابع
در مثال 1، بدون رسم نمودار \(\Large g\) و \(\Large h\) و بدون استفاده از روش تبدیل نمودار توابع نیز میتوانستیم برد آنها را به دست آوریم. در مثال 1، برد \(\Large f\) برابر با \(\Large [-1, 1]\) است. بنابراین داریم:
\(\Large -1\leq f(x) \leq 1\)
\(\Large \Rightarrow -2\leq 2f(x) \leq 2\)
پس برد \(\Large g(x)=2f(x)\) برابر است با \(\Large [-2, 2]\). همچنین برای \(\Large h(x)=-\frac{1}{2}f(x)\) داریم:
\(\Large -1\leq f(x) \leq 1\)
\(\Large \Rightarrow -\frac{1}{2}\leq -\frac{1}{2}f(x) \leq \frac{1}{2}\)
پس برد \(\Large h(x)=-\frac{1}{2}f(x)\) برابر است با \(\Large [-\frac{1}{2}, \frac{1}{2}]\).
نمودار \(\Large f(kx)\)
فرض کنید نمودار تابع \(\Large f(x)\) به شکل زیر است:
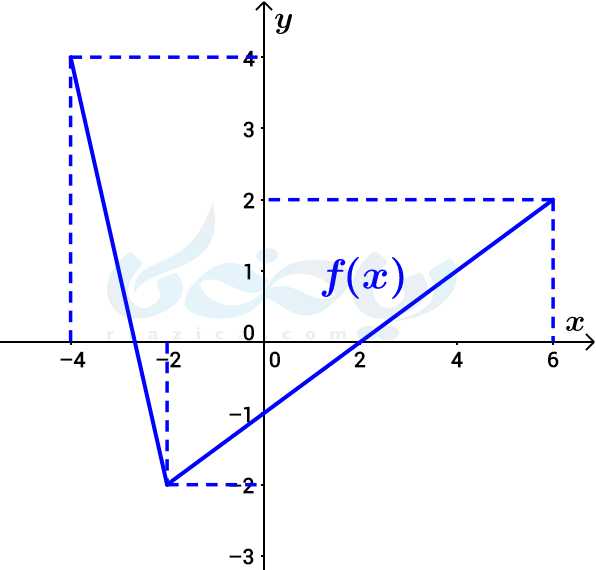
میخواهیم نمودار تابع \(\Large y=f(2x)\) را با استفاده از نمودار تابع \(\Large f(x)\) رسم کنیم. اگر \(\Large x\) برابر با \(\Large \frac{-4}{2}\) باشد، \(\Large f(2x)\) برابر با \(\Large f(-4)\) خواهد بود. همین طور اگر \(\Large x\) را به ترتیب \(\Large \frac{-2}{2}\) و \(\Large \frac{6}{2}\) در نظر بگیریم، \(\Large f(2x)\) به ترتیب برابر با \(\Large f(-2)\) و \(\Large f(6)\) خواهد بود. مقادیر \(\Large f(-4)\) و \(\Large f(-2)\) و \(\Large f(6)\) در نمودار بالا مشخص است. اگر این سه نقطه را به یکدیگر وصل کنیم، نمودار تابع \(\Large y=f(2x)\) به صورت زیر به دست میآید:
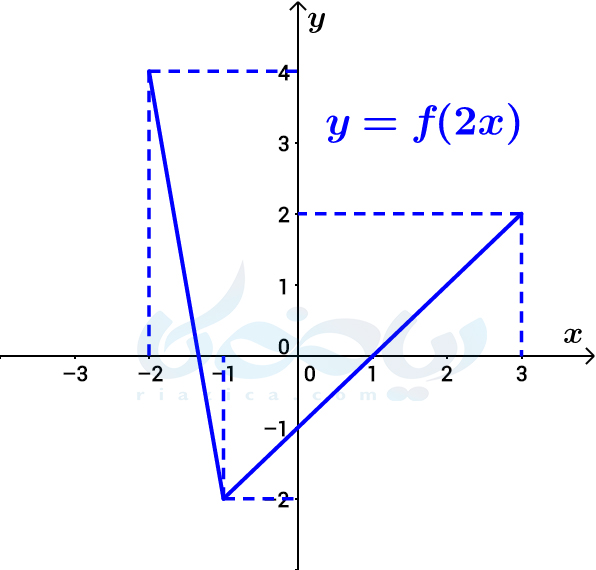همانطور که میبینید اگر طول هر نقطه از نمودار \(\Large f(x)\) را \(\Large \frac{1}{2}\) برابر کنیم، نمودار تابع \(\Large y=f(2x)\) که در شکل بالا رسم شده، به دست میآید.
انقباض و انبساط
همانطور که دیدید، برای رسم نمودار تابع \(\Large y=f(2x)\) با استفاده از روش تبدیل نمودار توابع کافی است طول هر نقطه از نمودار تابع \(\Large f(x)\) را در \(\Large \frac{1}{2}\) ضرب کنیم. به طور کلی برای رسم نمودار تابع \(\Large y=f(kx)\) کافی است طول هر نقطه از نمودار \(\Large f(x)\) را در \(\Large \frac{1}{k}\) ضرب کنیم. در این صورت سه حالت کلی پیش خواهد آمد:
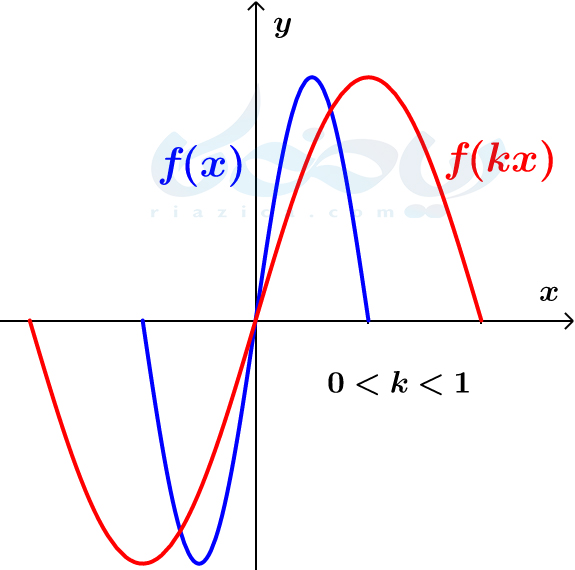
- \(\Large k\) عددی بین \(\Large 0\) و \(\Large 1\) است. در این حالت، نمودار تابع \(\Large y=f(kx)\) از انبساط افقی نمودار \(\Large f\) به دست آمده و به شکل زیر خواهد شد:
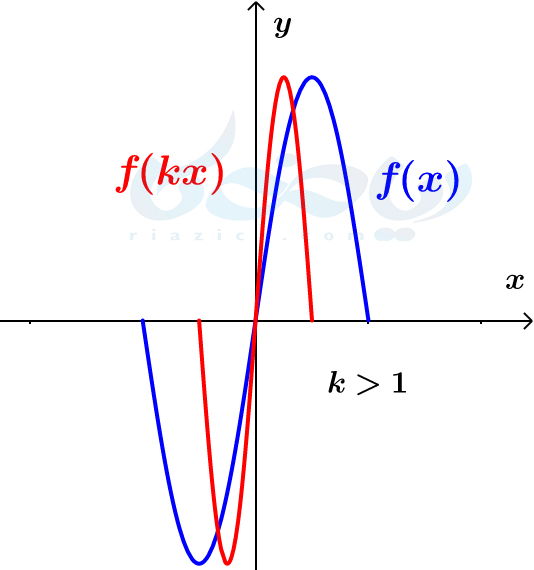
- \(\Large k\) عددی بزرگتر از \(\Large 1\) است. در این حالت، نمودار تابع \(\Large y=f(kx)\) از انقباض افقی نمودار تابع \(\Large f(x)\) به دست آمده و به شکل زیر خواهد شد:
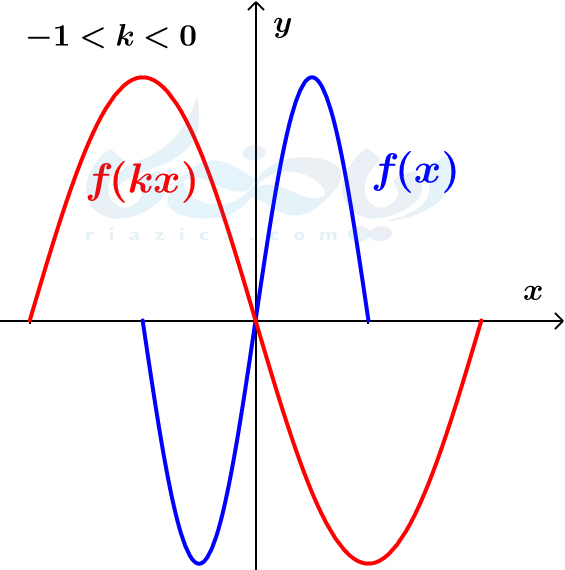
- \(\Large k\) عددی منفی است. در این حالت، ابتدا نمودار تابع \(\Large f(x)\) را نسبت به محور \(\Large y\)ها قرینه میکنیم. ، اگر \(\Large k\) بین \(\Large 0\) و \(\Large -1\) باشد، نمودار را منبسط و اگر \(\Large k\) کوچکتر از \(\Large -1\) باشد، نمودار را منقبض میکنیم. نمودار هر دو حالت در دو شکل زیر رسم شده است.
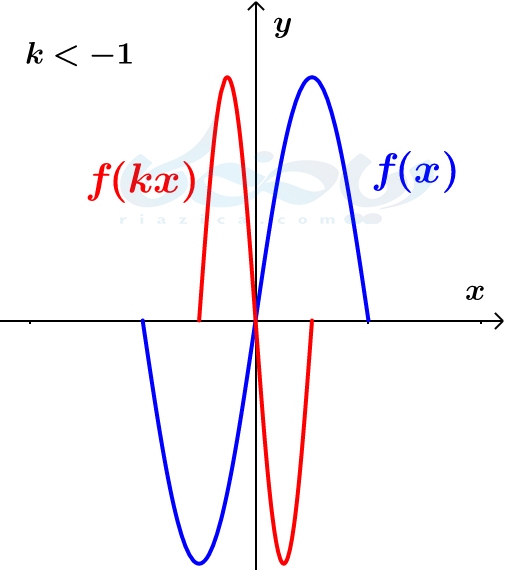
ریشهها
فرض کنیم به ازای \(\Large x_0\) مقدار \(\Large f(x_0)\) برابر با صفر شود. در این صورت به ازای \(\Large \frac{x_0}{k}\)، مقدار \(\Large f(k\frac{x_0}{k})\) برابر با \(\Large f(x_0)\) خواهد بود و از آنجاییکه \(\Large f(x_0)\) صفر است، \(\Large f(k\frac{x_0}{k})\) نیز صفر خواهد شد. پس اگر ریشههای معادلۀ \(\Large f(x)=0\) را در \(\Large \frac{1}{k}\) ضرب کنیم، ریشههای معادلۀ \(\Large f(kx)=0\) به دست میآید.
دامنه و برد
همان طور که گفتیم، نمودار تابع \(\Large y=f(kx)\) از ضرب طول نقاط نمودار \(\Large f(x)\) در \(\Large \frac{1}{k}\) به دست میآید و برد تابع \(\Large y=f(kx)\) نسبت به برد تابع \(\Large y=f(x)\) تغییری نخواهد کرد. اما دامنۀ \(\Large f(kx)\) چه طور؟ به دو مثال زیر توجه کنید.
مثال 3: در شکل زیر نمودار تابع \(\Large f(x)=\sqrt{1-x^2}\) رسم شده است. نمودار توابع \(\Large g(x)= f(2x)\) و \(\Large h(x)=f(-\frac{1}{2}x)\) را با استفاده از نمودار تابع \(\Large f(x)\) به دست آورده و دامنۀ هر یک را مشخص کنید.
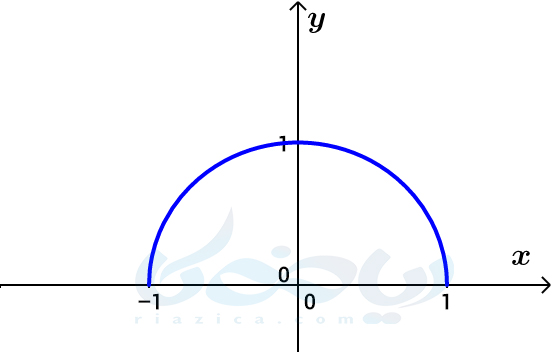
حل: همانطور که گفتیم، نمودار تابع \(\Large g(x)=f(2x)\) از انقباض افقی \(\Large f\) و نمودار تابع \(\Large h(x)=f(-\frac{1}{2}x)\) از قرینه نسبت به محور \(\Large y\)ها و سپس انبساط افقی \(\Large f\) به دست میآید. از آنجاییکه نمودار \(\Large f\) نسبت به محور \(\Large y\)ها متقارن است، قرینه کردن آن نسبت به محور \(\Large y\)ها تاثیری ندارد. بنابراین نمودار دو تابع \(\Large g(x)\) و \(\Large h(x)\) به صورت زیر خواهد بود:
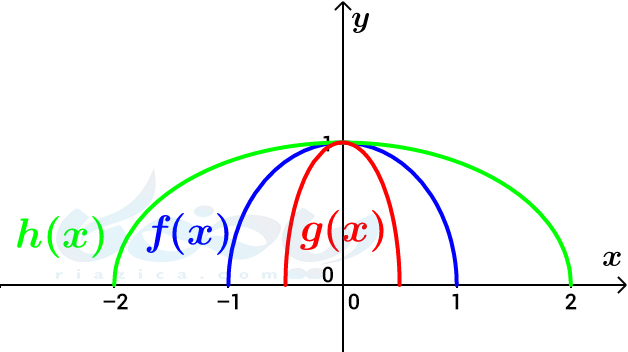
همان طور که میبینیم، دامنۀ تابع \(\Large f(x)\) برابر با \(\Large [-1, 1]\)، دامنۀ \(\Large g(x)\) برابر با \(\Large [-\frac{1}{2}, \frac{1}{2}]\) و دامنۀ \(\Large h(x)\) برابر با \(\Large [-2, 2]\) است.
مثال 4: در شکل زیر نمودار تابع \(\Large f(x)=x+1\) رسم شده است. نمودار توابع \(\Large g(x)=f(2x)\) و \(\Large h(x)=f(-\frac{1}{2}x)\) را به دست آورده و دامنۀ هر یک را مشخص کنید.
حل: نمودار \(\Large g(x)=f(2x)\) را با انقباض افقی \(\Large f\) و نمودار تابع \(\Large h(x)=f(-\frac{1}{2}x)\) را با قرینه کردن و انبساط افقی \(\Large f\) به صورت زیر رسم میکنیم.
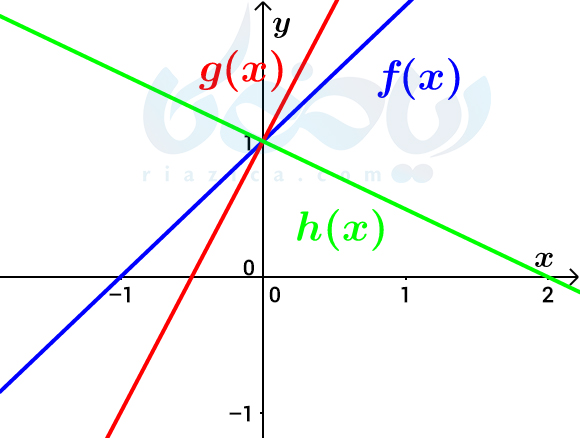
همان طور که میبینید، دامنۀ هر سه تابع \(\Large f(x)\) و \(\Large g(x)=f(2x)\) و \(\Large h(x)=f(-\frac{1}{2}x)\) برابر با \(\Large \mathbb{R}\) است.
با توجه به این دو مثال، نمیتوان یک رابطۀ کلی بین دامنۀ تابع \(\Large f(x)\) و تابع \(\Large y=f(kx)\) به دست آورد. در مثال 4، دامنۀ سه تابع برابر بود، اما در مثال 3 این اتفاق رخ نداد.
پیدا کردن دامنه بدون تبدیل نمودار توابع
در مثال 3، بدون رسم نمودار \(\Large g\) و \(\Large h\) و بدون استفاده از روش تبدیل نمودار توابع نیز میتوانستیم دامنۀ آنها را به دست آوریم. در مثال 3، دامنۀ \(\Large f\) برابر با \(\Large [-1, 1]\) است. بنابراین برای \(\Large f(2x)\) باید داشته باشیم:
\(\Large -1\leq 2x \leq 1\)
\(\Large \Rightarrow -\frac{1}{2}\leq x \leq \frac{1}{2}\)
پس دامنۀ \(\Large g(x)=f(2x)\) برابر است با \(\Large [-\frac{1}{2}, \frac{1}{2}]\). همچنین برای \(\Large f(-\frac{1}{2}x)\) باید داشته باشیم:
\(\Large -1\leq -\frac{1}{2}x \leq 1\)
\(\Large \Rightarrow -2\leq x \leq 2\)
پس دامنۀ \(\Large h(x)=f(-\frac{1}{2}x)\) برابر است با \(\Large [-2, 2]\).
نمودار \(\Large |f|\) در مبحث تبدیل نمودار توابع
برای رسم نمودار \(\Large |f|\) با استفاده از روش تبدیل نمودار توابع ابتدا نمودار را تعیین علامت میکنیم. به ازای \(\Large f(x)\)های مثبت، مقدار خود تابع و به ازای \(\Large f(x)\)های منفی، قرینۀ آنها را قرار میدهیم. یعنی در قسمتهایی که نمودار \(\Large f\) بالای محور \(\Large x\)هاست، خود نمودار و در قسمتهایی که زیر محور \(\Large x\)هاست، قرینۀ نمودار را نسبت به محور \(\Large x\)ها رسم کنیم.
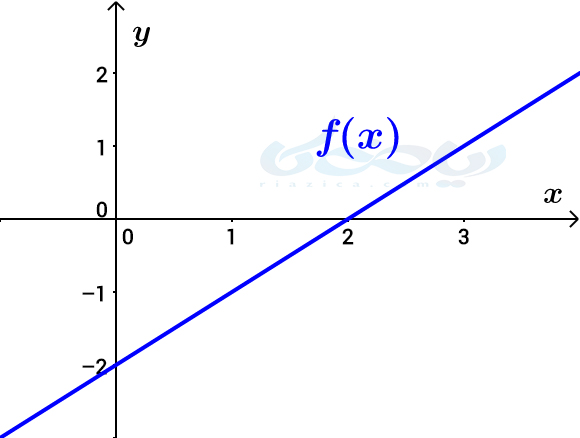
مثال 5: نمودار تابع \(\Large f(x)=x-2\) در شکل زیر رسم شده است. نمودار تابع \(\Large y=|f(x)|\) را رسم کنید.
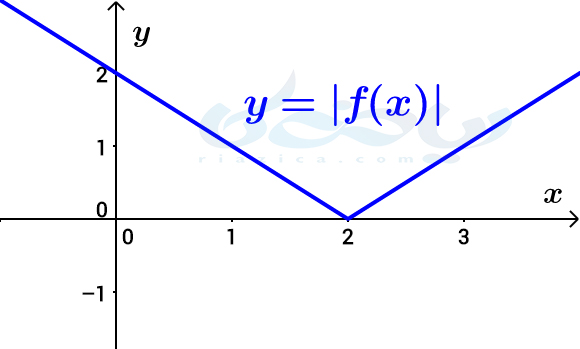
حل: به ازای \(\Large x> 2\)، مقدار \(\Large f(x)\) مثبت بوده و نمودار \(\Large f\) بالای محور \(\Large x\)هاست، اما به ازای \(\Large x<2\)، مقدار \(\Large f(x)\) منفی است و نمودار \(\Large f\) پایین محور \(\Large x\)هاست. پس، در \(\Large x> 2\) خود نمودار و در \(\Large x< 2\) قرینۀ نمودار نسبت به محور \(\Large x\)ها را رسم میکنیم:
توصیه میشه قبل خوندن این پست ،پست ترکیب توابع ریاضی دوازدهم را بخوانید ودر ادامه پست تابع وارون را مطالعه کنید.
زنگ آخر کلاس تبدیل نمودار توابع
در این درسنامه، به مبحث تبدیل نمودار توابع دوازدهم تجربی پرداختیم. روش رسم نمودار توابع \(\Large y=kf(x)\) و \(\Large y=f(kx)\) و \(\Large y=|f(x)|\) را با استفاده از نمودار تابع \(\Large f(x)\) بررسی کردیم. همچنین، در مورد دامنه و برد و ریشههای توابع \(\Large y=kf(x)\) و \(\Large y=f(kx)\) بحث کردیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث تبدیل نمودار توابع دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.
خیلی عالی توضیح میدید ولی کاش می شد با فیلم این مبحث ها را یاد گرفت چون خیلی از بچه با فیلم بهتر یاد می گیرند
با سلام وعرض ادب
ممنون از نظر لطف شما در حال تهیه پکیجهای ویدیویی برای همه پایه ها هستیم
سلام،به عنوان دبیر ریاضی خیلی از مطالب تون که ساده و روان بود لذت بردم.
با سلام وعرض ادب
ممنون همکار محترم خوشحالیم که برای شما مفید بوده قدر زر زرگر شناسد قدر گوهر ،گوهری
سلام، وقتتون بخیر
ممنون از سایت خوبتون که انقدر ساده، ریاضیات رو با مثال برای ما دانش آموزان قابل فهم کرده ?
اگر میشه، درمورد توابع گلدونی هم یه سری مطالب اولیه اش رو قرار بدید، متشکرم
با سلام وادب
انشالله به زودی
سلام وقت بخیر دوره محاسبات ذهنی تهیه کردم اما باز نمیشه و یا میگه لینک در دسترس نیست چیکار باید کنم؟؟؟؟؟
سلام دوستدعزیز
مشکل رو برطرف کردیم
ممنون از سایت خوبتون
با سلام وادب ممنون از انرژی شما
عالییییی
با سلام ممنون از نظر شما
عالی بود،ممنون
ممنون از نظر شما