دستگاه معادلات خطی نهم 3️⃣🎢 – ۳ روش عالی برای حل!

در درسنامهٔ معادلات خطی ریاضی نهم قصد داریم دستگاه‌های معادلات خطی را معرفی کرده و روش حل آن‌ها را بررسی کنیم. به طور کلی معادلات خطی از  ضرایب ثابت و یا متغیرهایی با درجهٔ یک تشکیل شده‌اند. برای یادآوری بیشتر می‌توانید درسنامهٔ معادله خط ریاضی نهم را مرور کنید. اما دستگاه معادلات خطی چیست؟ در این درسنامه قصد داریم تا به همین سوال پاسخ دهیم. با ما تا انتها همراه باشید.

دستگاه معادلات خطی چیست؟

اگر به جای یک معادلهٔ خطی، چند معادلهٔ خطی با متغیرهای مشترک داشته باشیم، دستگاه معادلات خطی داریم. به اعدادی که در صورت جاگذاری در متغیرها در معادله صدق کنند، جواب دستگاه معادلات می‌گوییم. بگذارید مثال بزنیم. معادلهٔ \(\Large y=x+2\) خطی است. اگر به جای \(\Large x\) مقدار \(\Large 1\) و به جای \(\Large y\) مقدار \(\Large 2\) را قرار دهیم، رابطهٔ \(\Large y=x+2\) برقرار است. بنابراین به \(\Large x=1\) و \(\Large y=3\) یک جواب برای معادلهٔ \(\Large y=x+2\) می‌گوییم. معادلهٔ \(\Large y=x+2\)، دسته جواب‌های دیگری نیز دارد. مثلاً \(\Large x=2\) و \(\Large y=4\) نیز در معادله صدق می‌کنند. حال فرض کنید به جای یک معادله، دو معادله داشتیم و به دنبال \(\Large x\)ها و \(\Large y\)هایی بودیم که به طور همزمان در هر دو معادله صدق کنند. مثلاً فرض کنید دو معادلهٔ \(\Large y=2x+1\) و \(\Large y=x+3\) را داریم و به دنبال دسته جواب هایی هستیم که در هر دو صدق ‌کنند. در این صورت به \(\Large \begin{cases} y=2x+1 \\ y=x+3 \end{cases}\) دستگاه معادله خطی می‌گوییم. اگر مقدار \(\Large x\) را برابر با \(\Large 2\) و مقدار \(\Large y\) را برابر با \(\Large 5\) قرار دهیم، \(\Large x\) و \(\Large y\) در هر دو معادله صدق می‌کنند. در ادامهٔ درسنامه روش حل دستگاه‌های معادلات خطی را بررسی خواهیم کرد.

---

---

روش حل دستگاه معادلات خطی

از آنجاییکه در کتاب درسی، دستگاه‌هایی که دو معادله و دو متغیر دارند، بررسی می‌شوند، ما نیز به بررسی این دستگاه‌ها می‌پردازیم. البته روش حل دستگاه‌های دیگر نیز به همین صورت است. به طور کلی، برای حل دستگاه‌های معادلات خطی که دارای دو معادله و دو مجهول هستند، باید یک مجهول را به طریقی حذف کرده تا یک معادلهٔ یک مجهولی داشته باشیم. برای این کار، سه روش متداول وجود دارد:

• رسم نمودار
• روش حذفی (جمع دو معادله و حذف یکی از متغیرها)
• روش جایگزینی (به دست آوردن یک متغیر از یک معادله و قرار دادن آن در معادلهٔ دیگر)

در قسمت‌های بعدی از درسنامهٔ دستگاه معادلات خطی نهم ، هر یک از این سه روش را بررسی می‌کنیم.

حل دستگاه معادلات خطی با رسم نمودار

فرض کنید یک دستگاه معادلات خطی دارای دو معادله و دو مجهول داریم. در این صورت هر معادله نمایانگر یک خط در صفحه است. اگر با استفاده از معلوماتمان در درسنامهٔ معادله خط ریاضی نهم، هر خط را در صفحه رسم کنیم، در صورتی که دو خط دارای نقطه یا نقاط مشترک باشند، آن نقطه یا نقاط، جواب دستگاه معادلات خطی هستند. زیرا وجود نقطهٔ مشترک به معنای وجود \(\Large x\)ها و \(\Large y\)هایی است که در هر دو معادله صدق می‌کنند.

به طور کلی برای دو خط در صفحه، یکی از حالات زیر پیش می‌آید:

• دو خط با یکدیگر موازی هستند؛ در این صورت دو خط هیچگاه یکدیگر را قطع نکرده و دستگاه معادلات، جوابی ندارد.
• دو خط روی یکدیگر می‌افتند؛ در این صورت دو خط یکدیگر را در بی‌شمار نقطه قطع کرده و دستگاه معادلات، بی‌شمار جواب دارد.
• دو خط فقط در یک نقطه یکدیگر را قطع می‌کنند؛ در این صورت دستگاه معادلات نیز تنها یک جواب دارد.

هر یک از سه حالات بالا را با حل مثال و رسم نمودار خواهیم دید. به مثال بعدی از درسنامهٔ دستگاه معادلات خطی نهم توجه کنید.

مثال از حل دستگاه معادلات خطی با رسم نمودار

مثال 1: دستگاه معادلات خطی \(\Large \begin{cases} x+2y=2 \\ 3x+y=6 \end{cases}\) را با رسم نمودار حل کنید.

حل: باید هر یک از خطوط \(\Large x+2y=2\) و \(\Large 3x+y=6\) را رسم کرده و نقاط مشترکشان را به دست آوریم. برای رسم هر خط کافی است دو نقطه از آن خط را پیدا کنیم. اگر در معادلهٔ \(\Large x+2y=2\)، مقدار \(\Large x\) برابر با \(\Large 0\) باشد، \(\Large y=1\) خواهد بود. همچنین، اگر \(\Large x=-2\) باشد، \(\Large y=2\) خواهد بود. بنابراین از دو نقطهٔ \(\Large \begin{bmatrix} 0 \\ 1 \end{bmatrix}\) و \(\Large \begin{bmatrix} -2 \\ 2 \end{bmatrix}\) برای رسم خط \(\Large x+2y=2\) استفاده می‌کنیم. سراغ خط \(\Large 3x+y=6\) می‌رویم. اگر در معادلهٔ \(\Large 3x+y=6\) مقدار \(\Large x\) برابر با \(\Large 0\) باشد، \(\Large y=6\) خواهد بود. همچنین، اگر \(\Large x=1\) باشد، \(\Large y=3\) خواهد بود. بنابراین از دو نقطهٔ \(\Large \begin{bmatrix} 0 \\ 6 \end{bmatrix}\) و \(\Large \begin{bmatrix} 1 \\ 3 \end{bmatrix}\) برای رسم خط \(\Large 3x+y=6\) استفاده می‌کنیم. در نمودار زیر، هر دو خط را رسم کرده‌ایم.

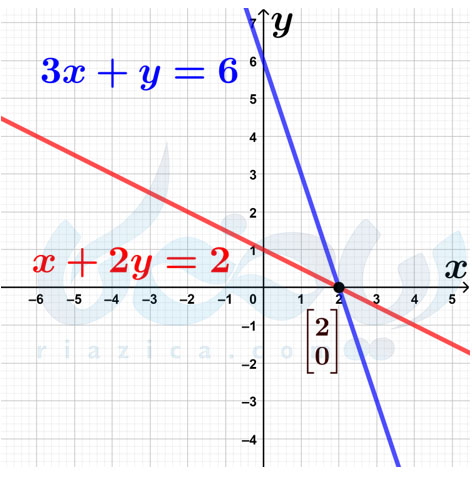
همان طور که در نمودار بالا می‌بینید، دو خط \(\Large x+2y=2\) و \(\Large 3x+y=6\) یکدیگر را در نقطهٔ \(\Large \begin{bmatrix} 2 \\ 0 \end{bmatrix}\) قطع می‌کنند. بنابراین نقطهٔ \(\Large \begin{bmatrix} 2 \\ 0 \end{bmatrix}\) تنها جواب دستگاه معادلات خطی \(\Large \begin{cases} x+2y=2 \\ 3x+y=6 \end{cases}\) است. به مثال بعدی توجه کنید.

مثال از حل دستگاه معادلات با رسم نمودار

مثال 2: جواب‌های دستگاه معادلات خطی \(\Large \begin{cases} 2x+3y=5 \\ 4x+6y=10 \end{cases}\) را با رسم نمودار بیابید.

حل: مانند مثال قبل، از هر خط دو نقطه انتخاب کرده و خطوط را رسم می‌کنیم. اگر در معادلهٔ \(\Large 2x+3y=5\)، مقدار \(\Large x\) برابر با \(\Large -2\) باشد، \(\Large y=3\) خواهد بود. همچنین، اگر \(\Large x=1\) باشد، \(\Large y=1\) خواهد بود. بنابراین از دو نقطهٔ \(\Large \begin{bmatrix} -2 \\ 3 \end{bmatrix}\) و \(\Large \begin{bmatrix} 1 \\ 1 \end{bmatrix}\) برای رسم خط \(\Large 2x+3y=5\) استفاده می‌کنیم. سراغ خط \(\Large 4x+6y=10\) می‌رویم. اگر \(\Large x=4\) باشد، \(\Large y=-1\) خواهد بود. همچنین، اگر \(\Large x=1\) باشد، \(\Large y=1\) خواهد بود. بنابراین از دو نقطهٔ \(\Large \begin{bmatrix} 4 \\ -1 \end{bmatrix}\) و \(\Large \begin{bmatrix} 1 \\ 1 \end{bmatrix}\) برای رسم خط \(\Large 4x+6y=10\) استفاده می‌کنیم. با استفاده از نقاطی که پیدا کردیم، خطوط را رسم می‌کنیم:

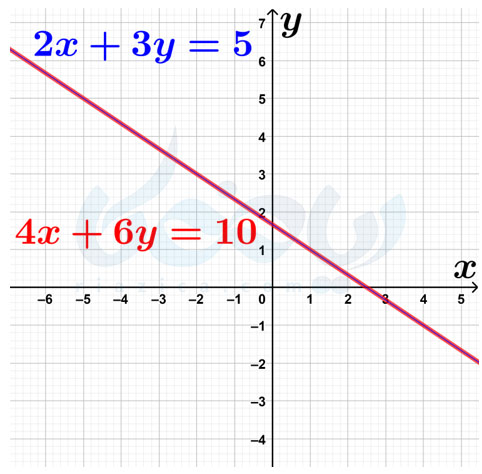
همان طور که دیدید، دو خط بر یکدیگر منطبق شدند. یعنی در واقع هر دو معادله خط، نمایانگر یک خط هستند. این را بدون رسم خطوط نیز می‌توانستیم متوجه شویم. اگر دقت کنید، معادلهٔ \(\Large 4x+6y=10\) از ضرب معادلهٔ \(\Large 2x+3y=5\) در عدد \(\Large 2\) به وجود می‌آید. می‌دانیم اگر دو طرف یک معادله را در یک عدد ضرب کنیم، جواب‌های معادله تغییر نمی‌کنند. بنابراین، هر دو معادله یکی هستند و به همین دلیل دو خط روی هم می‌افتند. بنابراین جواب‌های دستگاه معادله خطی \(\Large \begin{cases} 2x+3y=5 \\ 4x+6y=10 \end{cases}\) برابر است با تمام نقاط روی خط \(\Large 2x+3y=5\). در نتیجه این دستگاه بی‌شمار جواب دارد.

مثال از حل دستگاه معادلات با رسم نمودار

مثال 3: جواب‌های دستگاه معادلات خطی \(\Large \begin{cases} x-2y=4 \\ 2x-4y=-4 \end{cases}\) را با رسم نمودار بیابید.

حل: مانند دو مثال قبل، از هر خط دو نقطه پیدا کرده و خطوط را رسم می‌کنیم. نقاط \(\Large \begin{bmatrix} 0 \\ -2 \end{bmatrix}\) و \(\Large \begin{bmatrix} 4 \\ 0 \end{bmatrix}\) روی خط \(\Large x-2y=4\) و نقاط \(\Large \begin{bmatrix} 0 \\ 1 \end{bmatrix}\) و \(\Large \begin{bmatrix} -2 \\ 0 \end{bmatrix}\) روی خط \(\Large 2x-4y=-4\) قرار دارند. اگر خطوط را رسم کنیم، شکل زیر حاصل می‌شود:

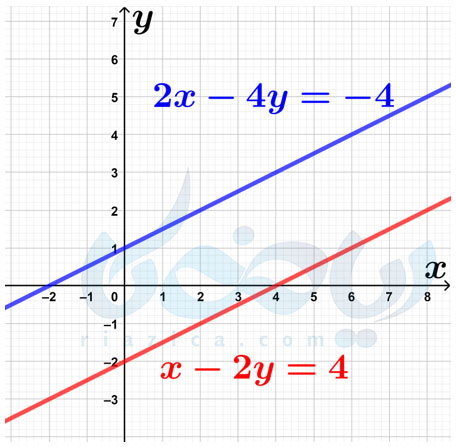
همان طور که می‌ببینید، دو خط موازی هستند. این بار اگر دقت کنید می‌بینید که ضرایب \(\Large x\) و \(\Large y\) در معادلهٔ \(\Large 2x-4y=-4\) از ضرب ضرایب \(\Large x\) و \(\Large y\) معادلهٔ \(\Large x-2y=4\) در \(\Large 2\) به دست آمده‌اند. اما مقدار ثابت دو معادله در طرف راست آن‌ها که \(\Large 4\) و \(\Large -4\) است، چنین نسبتی با هم ندارند. به عبارت دیگر، شیب دو خط با هم برابر است اما عرض از مبدأ آن‌ها با یکدیگر تفاوت دارد (در صورتی که نحوهٔ به دست آوردن شیب خط و عرض از مبدأ را فراموش کرده‌اید، درسنامهٔ شیب خط و عرض از مبدأ ریاضی نهم را مرور کنید). شیب خط \(\Large x-2y=4\) برابر با \(\Large \frac{1}{2}\) و عرض از مبدأ آن برابر با \(\Large -2\) است. شیب خط \(\Large 2x-4y=-4\) نیز برابر با \(\Large \frac{1}{2}\) اما عرض از مبدأ آن برابر با \(\Large 1\) است.  در نتیجه هرگاه یک دستگاه معادلات خطی با دو معادله و دو مجهول داشتیم که ضرایب \(\Large x\) و \(\Large y\) یک معادله از ضرب ضرایب \(\Large x\) و \(\Large y\) معادلهٔ دیگر به دست آمد، اما بین مقادیر ثابت چنین رابطه‌ای وجود نداشت، دو خط با یکدیگر موازی بوده و دستگاه معادلات خطی بدون جواب است. به قسمت بعدی از درسنامهٔ دستگاه معادلات خطی ریاضی نهم توجه کنید.

نتیجه‌گیری از سه مثال قبل

با توجه به آنچه در سه مثال قبل دیدیم، می‌توان نتیجه گرفت که در یک دستگاه معادلات خطی با دو معادلهٔ دو متغیره، اگر خطوط یکدیگر را در یک نقطه قطع کنند، دستگاه یک جواب دارد. اگر خطوط بر یکیگر منطبق باشند، دشتگاه بی‌شمار جواب دارد. اگر خطوط با یکدیگر موازی باشند، دستگاه جوابی ندارد.

حل دستگاه معادلات خطی به روش حذفی

برای حل دستگاه معادلات خطی می‌توان معادلات را با یکدیگر جمع کرده تا یکی از متغیرها حذف شود و دستگاه تبدیل به یک معادلهٔ یک مجهولی گردد. به این روش، روش حذفی می‌گوییم. اما منظور از جمع معادلات و حذف متغیر چیست؟ فرض کنید می‌خواهیم دستگاه \(\Large \begin{cases} x+y=2 \\ x-y=4 \end{cases}\) را حل کنیم. در این صورت، طرف‌های چپ دو معادله را با هم و طرف‌های راست را با هم جمع کرده و با یکدیگر برابر قرار می‌دهیم. برای اینکه بهتر متوجه شوید به تصویر پایین دقت کنید:

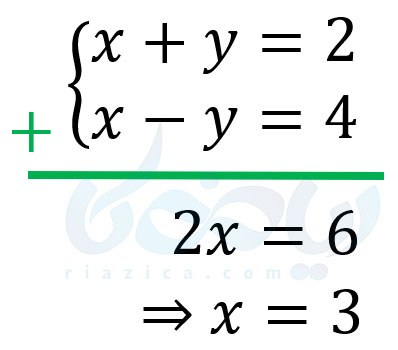
همان طور که دیدید، با انجام این کار، دستگاه به معادلهٔ یک مجهولی \(\Large 2x=6\) تبدیل می‌شود. پاسخ این معادلهٔ یک مجهولی نیز، \(\Large x=3\) است. حال کافی است به دستگاه اولیه برگردیم و مقدار \(\Large x\) را در یکی از معادلات، برابر با \(\Large 3\) قرار دهیم. مثلاً، کافی است در معادلهٔ \(\Large x+y=2\) که در دستگاه، قبل از جمع معادلات وجود داشت، مقدار \(\Large x\) را برابر با \(\Large 3\) قرار دهیم. در این صورت داریم:

\(\LARGE 3+y=2\)

\(\LARGE \Rightarrow y=-1\)

در نتیجه، \(\Large \begin{bmatrix} 3 \\ -1 \end{bmatrix}\) جواب دستگاه معادلات خطی است. باید توجه داشت که گاهی لازم است ابتدا یکی از معادلات را در یک عدد مناسب ضرب کرده و سپس با معادلهٔ دوم جمع کنیم. برای پیدا کردن عدد مناسب، ابتدا ببینید چه متغیری را می‌خواهید حذف کنید. مثلاً فرض کنید می‌خواهیم متغیر \(\Large x\) را در دو معادله حذف کنیم. باید یکی از معادلات را در عددی ضرب ‌کنیم به طوری که ضریب \(\Large x\) در دو معادله قرینهٔ یکدیگر شود. در انتها دو معادله را با یکدیگر جمع می‌کنیم تا متغیری که مد نظرمان بود حذف گردد. برای اینکه بهتر متوجه شوید، به مثال‌های بعدی از درسنامهٔ دستگاه معادلات خطی نهم توجه کنید.

---

---

مثال از حل دستگاه به روش حذفی

مثال 4:دستگاه معادلات خطی \(\Large \begin{cases} 2x-5y=2 \\ 4x+3y=17 \end{cases}\) را حل کنید.

حل: سعی می کنیم متغیر \(\Large x\) را از دو معادله حذف کنیم. ضریب متغیر \(\Large x\) در معادلهٔ اول برابر با \(\Large 2\) و در معادلهٔ دوم برابر با \(\Large 4\) است. بنابراین، کافی است معادلهٔ اول را در عدد \(\Large -2\) ضرب کنیم تا ضریب \(\Large x\) در دو معادله، قرینهٔ یکدیگر شود. به این ترتیب داریم:

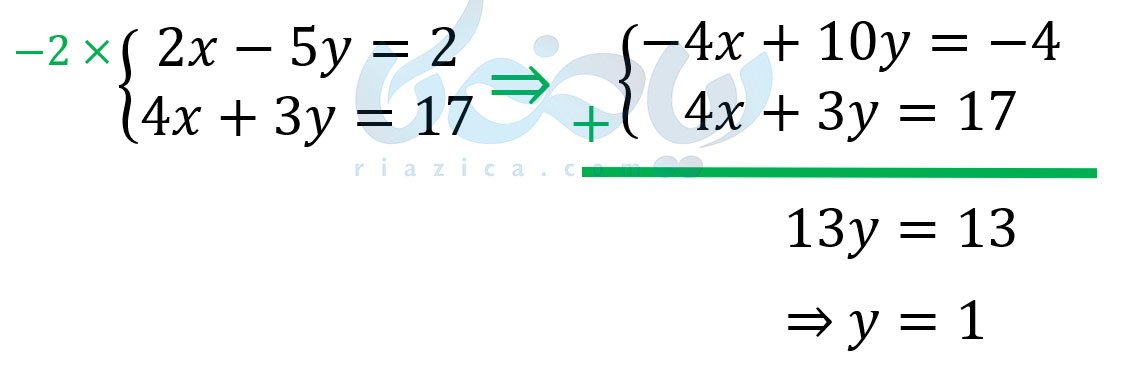
حال باید \(\Large y\) را در یکی از معادلات دستگاه برابر با \(\Large 1\) قرار داده تا \(\Large x\) را به دست آوریم. معادلهٔ \(\Large 2x-5y=2\) را برای این کار انتخاب می‌کنیم. بنابراین داریم:

\(\LARGE 2x-5=2\)

\(\LARGE \Rightarrow 2x=7\)

\(\LARGE \Rightarrow x=\frac{7}{2}\)

در نتیجه، \(\Large y=1\) و \(\Large x=\frac{7}{2}\) جواب دستگاه معادلات خطی ماست.

مثال از حل دستگاه معادلات خطی به روش حذفی

مثال 5: جواب‌های دستگاه معادلات خطی \(\Large \begin{cases} \frac{x}{3}+\frac{y}{2}=3 \\ -\frac{2x}{9}+\frac{y}{6}=-1 \end{cases}\) را بیابید.

حل: این بار سعی می‌کنیم متغیر \(\Large y\) را حذف کنیم. ضریب متغیر \(\Large y\) در معادلهٔ اول برابر با \(\Large \frac{1}{2}\) و در معادلهٔ دوم برابر با \(\Large \frac{1}{6}\) است. بنابراین، کافی است معادلهٔ دوم را در عدد \(\Large -3\) ضرب کنیم تا ضریب \(\Large y\) در دو معادله، قرینهٔ یکدیگر شود. به این ترتیب داریم:

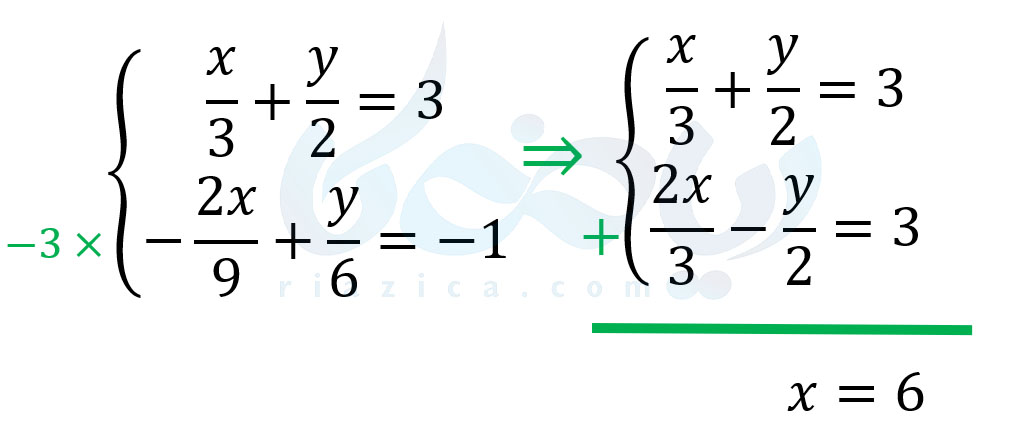
بنابراین \(\Large x=6\) است. حال باید مقدار \(\Large x\) را در یکی از معادلات دستگاه برابر با \(\Large 6\) قرار داده و \(\Large y\) را به دست آوریم. معادلهٔ \(\Large \frac{x}{3}+\frac{y}{2}=3\) را برای این کار انتخاب می‌کنیم. بنابراین داریم:

\(\LARGE 2+\frac{y}{2}=3\)

\(\LARGE \Rightarrow \frac{y}{2}=3-2=1\)

\(\LARGE \Rightarrow y=2\)

در نتیجه، \(\Large \begin{bmatrix} 6 \\ 2 \end{bmatrix}\) جواب دستگاه معادلات خطی ماست.

حل دستگاه معادلات خطی با جایگزینی

به غیر از دو روشی که برای حل دستگاه معادلات خطی معرفی کردیم، یعنی رسم نمودار و جمع معادلات، روش دیگری نیز برای پیدا کردن جواب‌های یک دستگاه وجود دارد. در این روش که آن را روش جایگزینی می‌نامیم، مقدار یکی از متغیر‌ها را در یکی از معادلات، بر حسب متغیرهای دیگر به دست آورده و در معادلهٔ دیگر قرار می‌دهیم. به طور مثال فرض کنید می‌خواهیم دستگاه معادلات خطی \(\Large \begin{cases} -x+y=2 \\ x+y=6 \end{cases}\) را با روش جایگزینی حل کنیم. در معادلهٔ اول، متغیر \(\Large x\) را بر حسب متغیر \(\Large y\) می‌نویسیم:

\(\LARGE -x+y=2\)

\(\LARGE \Rightarrow x=y-2\)

حال، عبارت \(\Large y-2\) را به جای \(\Large x\) در معادلهٔ \(\Large x+y=6\) قرار می‌دهیم. به این ترتیب داریم:

\(\LARGE x+y=6\)

\(\LARGE \Rightarrow (y-2)+y=6\)

\(\LARGE \Rightarrow 2y=8\)

\(\LARGE \Rightarrow y=4\)

همان طور که دیدید دستگاه معادلات به یک معادلهٔ یک مجهولی تبدیل شد و از این طریق مقدار \(\Large y\) به دست آمد. از طرفی \(\Large x\) را بر حسب \(\Large y\) نوشته بودیم. بنابراین با داشتن \(\Large y\) می‌توانیم \(\Large x\) را نیز به دست آوریم. یعنی داریم:

\(\LARGE x=y-2\)

\(\LARGE \Rightarrow x=4-2=2\)

مثال از حل دستگاه معادلات با جایگزینی

مثال 6: دستگاه معادلات خطی \(\Large \begin{cases} 3x-2y=1 \\ 2x+y=3 \end{cases}\) را حل کنید.

حل: در معادلهٔ دوم، متغیر \(\Large y\) را بر حسب متغیر \(\Large x\) می‌نویسیم:

\(\LARGE 2x+y=3\)

\(\LARGE \Rightarrow y=3-2x\)

حال، عبارت \(\Large 3-2x\) را به جای \(\Large y\) در معادلهٔ \(\Large 3x-2y=1\) قرار می‌دهیم. به این ترتیب داریم:

\(\LARGE 3x-2y=1\)

\(\LARGE \Rightarrow 3x-2(3-2x)=1\)

\(\LARGE \Rightarrow 3x-6+4x=1\)

\(\LARGE \Rightarrow 7x=7\)

\(\LARGE \Rightarrow x=1\)

بنابراین مقدار \(\Large x\) برابر با \(\Large 1\) است. حال کافی است به جای \(\Large x\) در رابطهٔ \(\Large y=3-2x\) مقدار \(\Large 1\) را قرار دهیم تا \(\Large y\) نیز به دست آید. به این ترتیب، مقدار \(\Large y\) برابر با \(\Large 3-2\) یعنی \(\Large 1\) خواهد شد.

مثال از حل دستگاه معادلات با جایگزینی

مثال 7: جواب های دستگاه معادلات خطی \(\Large \begin{cases} 2x+3y=4 \\ 4x+5y=3 \end{cases}\) را بیابید.

حل: هیچ تفاوتی نمی‌کند که کدام متغیر را از کدام معادله انتخاب کرد و بر اساس متغیر دیگر بنویسیم. معادلهٔ اول و متغیر \(\Large x\)  را برای این کار انتخاب می‌کنیم:

\(\LARGE 2x+3y=4\)

\(\LARGE \Rightarrow 2x=4-3y\)

\(\LARGE \Rightarrow x=\frac{4-3y}{2}\)

حال، عبارت \(\Large \frac{4-3y}{2}\) را به جای \(\Large x\) در معادلهٔ \(\Large 4x+5y=3\) قرار می‌دهیم. به این ترتیب داریم:

\(\LARGE 4x+5y=3\)

\(\LARGE \Rightarrow 4 \times \frac{4-3y}{2} +5y=3 \)

\(\LARGE \Rightarrow 2(4-3y) +5y=3 \)

\(\LARGE \Rightarrow 8-6y+5y=3 \)

\(\LARGE \Rightarrow 8-y=3 \)

\(\LARGE \Rightarrow y=5 \)

بنابراین مقدار \(\Large y\) برابر با \(\Large 5\) است. حال کافی است به جای \(\Large y\) در رابطهٔ \(\Large x=\frac{4-3y}{2}\) مقدار \(\Large 5\) را قرار دهیم تا \(\Large x\) نیز به دست آید. به این ترتیب، مقدار \(\Large x\) برابر با \(\Large \frac{4-15}{2}\) یعنی \(\Large \frac{-11}{2}\) است.

زنگ آخر کلاس

در درسنامه‌ای که از ریاضی نهم خواندیم، ابتدا با دستگاه معادلات خطی آشنا شدیم. همان طور که دیدیم، دستگاه معادلات خطی را می‌توان یا با رسم نمودار، یا با جمع معادلات یا با استفاده از روش جایگزینی حل کرد. در حل دستگاه با استفاده از رسم نمودار دیدیم که برای یک دستگاه با دو معادله و دو مجهول، سه حالت ممکن است رخ دهد. یا دستگاه جواب نداشته باشد، یا یک جواب داشته باشد و یا بی شمار جواب داشته باشد.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با این مبحث دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.  

---

---