آموزش ریاضی پایه هفتم
شمارنده اول ریاضی هفتم 1️⃣🌐 – اعداد اولشو بشمار!
در درسنامۀ شمارنده اول ریاضی هفتم ابتدا منظورمان از شمارندۀ اول را بیان میکنیم. سپس، روش تجزیۀ یک عدد و به دست آوردن شمارنده های اول آن را نشان میدهیم. در انتها نیز، کاربرد تجزیۀ اعداد در ساده کردن صورت و مخرج کسر را میبینیم. پیشنهاد میکنیم قبل از مطالعۀ این درسنامه، درسنامۀ عدد اول ریاضی هفتم را مطالعه کنید. سعی میکنیم با حل مثالهای مختلف، در درک بهتر این مبحث به شما کمک کنیم. با ما تا انتها همراه باشید.
شمارندۀ اول چیست؟
هر عدد طبیعی بزرگتر از \(\Large 1\) را میتوان به صورت حاصل ضرب تعدادی عدد اول نوشت. مثلاً عدد \(\Large 18\)، عددی طبیعی است و میتوان آن را به صورت \(\Large 2 \times 3 \times 3\) نوشت. به \(\Large 2\) و \(\Large 3\)، شمارنده های اول عدد \(\Large 18\) میگوییم.
برای علاقهمندان: اینکه هر عدد طبیعی بزرگتر از \(\Large 1\) را میتوان به صورت حاصل ضرب تعدادی عدد اول نوشت، نتیجهای است که با استفاده از قضیۀ اساسی حساب ثابت میشود. در صورتی که علاقهمندید، در مورد آن مطالعه کنید.
به مثال بعدی از درسنامۀ شمارنده اول ریاضی هفتم توجه کنید.
مثال از شمارنده اول ریاضی هفتم
مثال 1: چهار عدد بیابید که شمارندههای اولشان \(\Large 2\) و \(\Large 5\) باشد.
حل: کافی است \(\Large 2\) و \(\Large 5\) را به چهار صورت مختلف در هم ضرب کنیم (دقت کنید که مُجازیم از یک عدد اول به تعداد دلخواه در حاصل ضربی که مینویسیم استفاده کنیم):
\(\LARGE 2 \times 5 =10\)
\(\LARGE 2 \times 2 \times 5 =20\)
\(\LARGE 2 \times 5 \times 5 =50\)
\(\LARGE 2 \times 2 \times 5 \times 5 =100\)
در قسمت بعدی از درسنامۀ شمارنده اول ریاضی هفتم روش به دست آوردن شمارنده های اول یک عدد دلخواه را خواهیم آموخت.
تجزیۀ عدد و یافتن شمارنده های اول
گاهی لازم است که شمارنده های اول یک عدد را پیدا کنیم. برای این کار کافی است ابتدا عدد داده شده را به صورت حاصل ضرب دو عدد بنویسیم. سپس این کار را تا جایی ادامه دهیم که به شمارنده های اول عدد برسیم. مثلاً فرض کنید میخواهیم شمارنده های اول عدد \(\Large 12\) را پیدا کنیم. ابتدا عدد \(\Large 12\) را به صورت حاصل ضرب دو عدد \(\Large 3\) و \(\Large 4\) به صورت زیر مینویسیم:

عدد \(\Large 3\) که اول است و لازم نیست جلوتر برویم. به همین خاطر دور آن دایره کشیدیم. اما عدد \(\Large 4\) را میتوانیم به صورت حاصل ضرب \(\Large 2\) در خودش بنویسیم:
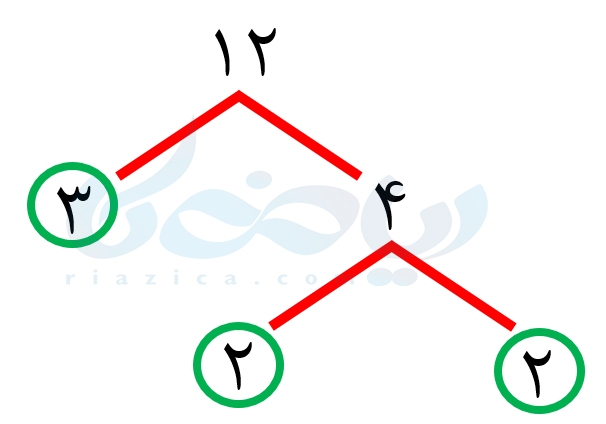
از این جلوتر نمیتوانیم برویم، زیرا به اعداد اول رسیدیم. بنابراین، با توجه به نمودار بالا، اعداد \(\Large 2\) و \(\Large 3\) شمارنده های اول عدد \(\Large 12\) هستند و عدد \(\Large 12\) را میتوانیم به صورت \(\Large 3 \times 2 \times 2\) بنویسیم. به این کار تجزیه و به نموداری که در بالا رسم کردیم، نمودار درختی میگوییم. به مثال بعدی از درسنامۀ شمارنده اول ریاضی هفتم توجه کنید.
مثال از تجزیۀ عدد به عوامل اول
مثال 2: با رسم نمودار درختی، شمارندههای اول عدد \(\Large 75\) را پیدا کنید.
حل: ابتدا عدد \(\Large 75\) را به صورت حاصل ضرب دو عدد مینویسیم. مثلاً \(\Large 3\) و \(\Large 25\) را در نظر میگیریم:
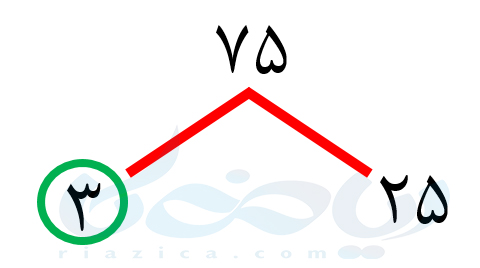
عدد \(\Large 3\)، عدد اول است. بنابراین تجزیه نمیشود. باید \(\Large 25\) را تجزیه کنیم. عدد \(\Large 25\) را به صورت حاصل ضرب \(\Large 5\) در \(\Large 5\) مینویسیم:
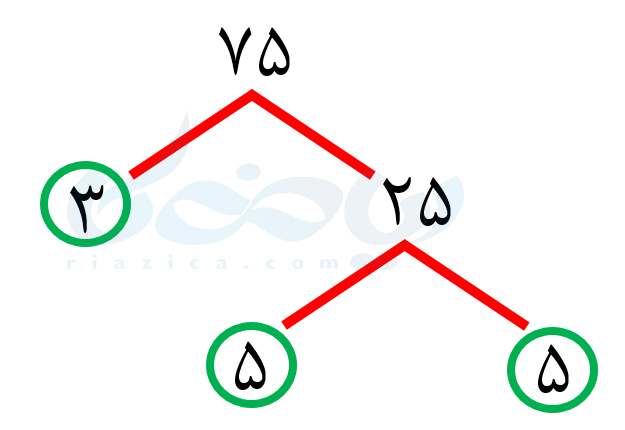
دیگر نمیتوانیم هیچ عددی را تجزیه کنیم، زیرا به عوامل اول رسیدهایم. با توجه به نمودار بالا، عدد \(\Large 75\) را میتوان به صورت \(\Large 5 \times 5 \times 3 \) نوشت. به مثال بعدی از درسنامۀ شمارنده اول ریاضی هفتم توجه کنید.
مثال از درسنامۀ شمارنده اول ریاضی هفتم
مثال 3: با رسم نمودار درختی، شمارندههای اول عدد \(\Large 72\) را پیدا کنید.
حل: ابتدا عدد \(\Large 72\) را به صورت حاصل ضرب دو عدد مینویسیم. مثلاً \(\Large 2\) و \(\Large 36\) را برای این کار انتخاب میکنیم:

عدد \(\Large 2\)، عدد اول است. بنابراین تجزیه نمیشود. باید \(\Large 36\) را تجزیه کنیم. میتوانیم \(\Large 36\) را به صورت حاصل ضرب \(\Large 9\) در \(\Large 4\) بنویسیم:
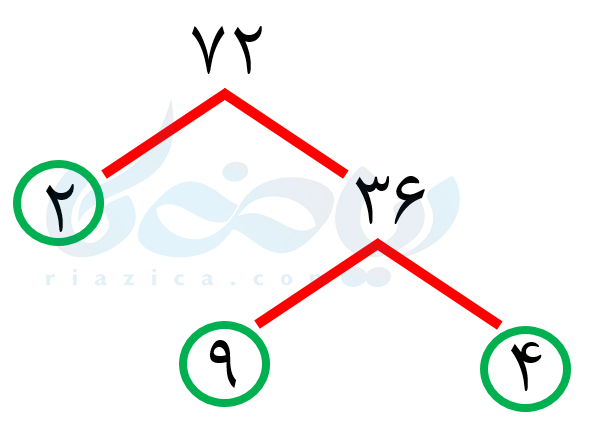
هم \(\Large 9\) تجزیه میشود و هم \(\Large 4\). عدد \(\Large 9\) را به صورت حاصل ضرب \(\Large 3\) در \(\Large 3\) و عدد \(\Large 4\) را به صورت حاصل ضرب \(\Large 2\) در \(\Large 2\) مینویسیم:

دیگر نمیتوانیم هیچ عددی را تجزیه کنیم، زیرا به عوامل اول رسیدهایم. با توجه به نمودار بالا، عدد \(\Large 72\) را میتوان به صورت \(\Large 2 \times 2 \times 2 \times 3 \times 3\) نوشت. به قسمت بعدی از درسنامۀ شمارنده اول ریاضی هفتم توجه کنید.
ساده کردن صورت و مخرج کسر
از تجزیۀ اعداد میتوان در ساده کردن صورت و مخرج کسرها نیز استفاده کرد. در واقع، بعد از پیدا کردن شمارندههای صورت و مخرج کسر، شمارندههای مشترک را ساده میکنیم. مثلاً کسر \(\Large \frac{18}{27}\) را در نظر بگیرید. میتوان صورت و مخرج کسر را به صورت زیر تجزیه کرد:
\(\LARGE \frac{18}{27}=\frac{9 \times 2}{9 \times 3}\)
عدد \(\Large 9\)، شمارندۀ مشترک صورت و مخرج کسر است و ساده میشود. بنابراین داریم:
\(\LARGE \frac{18}{27}=\frac{2}{3}\)
به مثال بعدی از درسنامۀ شمارنده اول ریاضی هفتم توجه کنید.
مثال از ساده کردن صورت و مخرج کسر
مثال 4: کسر \(\Large \frac{56}{72}\) را با تجزیۀ صورت و مخرج، ساده کنید.
حل: صورت کسر را میتوان به صورت \(\Large 8 \times 7\) و مخرج کسر را میتوان به صورت \(\Large 8 \times 9\) تجزیه کرد. بنابراین داریم:
\(\LARGE \frac{56}{72}=\frac{8 \times 7}{8 \times 9}\)
عدد \(\Large 8\)، شمارندۀ مشترک صورت و مخرج کسر است و ساده میشود. بنابراین داریم:
\(\LARGE \frac{56}{72}=\frac{7}{9}\)
توصیه میشه قبل از خوندن این مطلب پست اعداد اول ریاضی هفتم رو مطالعه کن ودر ادامه پست بزرگترین شمارنده مشترک ریاضی هفتم رو بخون.
زنگ آخر کلاس شمارنده اول ریاضی هفتم
در این درسنامه از ریاضی هفتم، شمارندههای اول را معرفی کردیم. همانطور که گفتیم، هر عدد طبیعی بزرگتر از \(\Large 1\) را میتوان به صورت حاصل ضرب اعداد اول نوشت. روش تجزیۀ اعداد با استفاده از نمودار درختی را بررسی کردیم. همچنین در انتهای درسنامه، کاربرد تجزیۀ اعداد در ساده کردن صورت و مخرج کسر را دیدیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با این مبحث دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





۹۸
بد نی
با سلام
خدا رو شکر
خیلی ممنون از درسنامه عالیتون
واقعا استفاده خوبی بردم.
فردا سر امتحان از این مبحث مطمئنم هیچ اشکالی ندارم.
واقعا سپاسگزارم
با سلام وادب
خوشحالیم که اینهمه برای شما مفید بوده
عالی بود
واقعا ممنون
خداقوت
با سلام وادب
ممنون ازنظرلطف شما
بسیار عالی هستین
با سلام و ادب
ممنون از نظر لطف شما
بسیار عالی هستین واقعا ممنونم درمورد حجم های منشوری هم بگید
با سلام وادب
ممنون از شما در مورد حجمهای منشوری هم پست داریم
با سلام دوست عزیز اینم لینک پست حجم های منشوریhttps://riazica.com/category/7th-grade-math/page/2/
عالی بود برای امتحان فردا خیلی بدردم میخوره مرسی
با سلام دوست عزیز
خوشحالیم که مفید بوده برای شما
۹ شمارنده ی اول نیست
با سلام
خیر عدد مرکب هست
بسیار عالی
وای ممنون خیلی خوب بود یعنی خوب که نه عالی بود! واقعا ممنون بابت این توضیحات
ممنون از توجه ودلگرمی شما