آموزش ریاضی پایه دهم
دامنه و برد تابع به زبان عکس‌ها ✅👨👧👧
اسفند
مبحث دامنه و برد تابع و پیداکردن آن‌ها با توجه به ضابطه و نمودار تابع مبحث مهمی است که گاهی حتی چالش برانگیز است. به خصوص پیداکردن برد همیشه کار ساده‌ای نیست. اما آنچه در کتاب آموزش ریاضی دهم بیشتر بر آن تاکید، پیداکردن دامنه و برد از روی نمودار است.
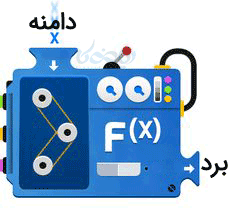
تعریف دامنه و برد در ریاضی دهم
همانطور که در نوشتار تابع و بازنمایی‌های آن مشاهده کردید، یک تابع را به چهار شکل می‌توان نمایش داد که یکی از آن‌ها زوج مرتب بود. حال مجموعه همه مؤلفه‌های اول زوج‌های مرتب تشکیل دهنده هر تابع را دامنه و مجموعه همهٔ مولفه‌های دوم را برد آن تابع می‌نامند.
نمایش دامنه و برد تابع از روی زوج‌های مرتب
در نوشتار تابع و بازنمایی‌های آن، یکی از اشکال نمایش تابع زوج مرتب بود. اگر همهٔ مولفه‌های اول را داخل یک مجموعه بنویسیم به آن دامنه می‌گویند. و اگر مولفه‌های دوم را داخل یک مجموعه بنویسیم بدان برد گفته میشود.
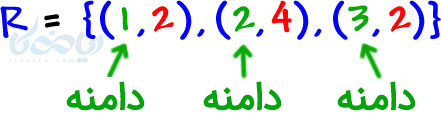
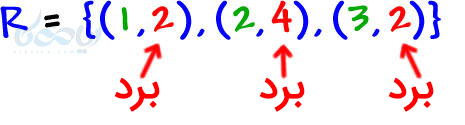
مثال۱: دامنه و برد توابع زیر را مشخص کنید؟
حل ۱:
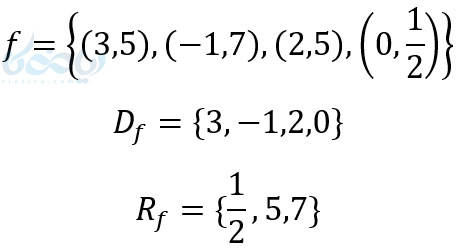
در آموزش ریاضی دهم یاد می‌گیریم، اگر تابع به صورت جدول نوشته شود مجموعه عضوهای ردیف اول دامنه و مجموعه عضوهای ردیف دوم برد نامیده میشود.
| ۲ | ۱ | ۰ | -۱ | -۲ | دامنه |
|---|---|---|---|---|---|
| ۴ | ۳ | ۲ | ۱ | ۰ | برد |
مثال ۲: دامنه و برد جدول زیر را مشخص کنید؟
حل ۲:
| 5 | -1 | -2 | \( \Large x \) |
|---|---|---|---|
| -2 | -3 | -2 | \( \Large f(x) \) |
\( \LARGE D_f=\{-2,-1,5\} \)
\( \LARGE R_f=\{-2,-3,-2\} \)
اگر تابع به صورت نمودار ون (پیکانی) نوشته شود همه اعضای \( \Large A \) دامنه و همه اعضای \( \Large B \) برد هستند.
مثال ۳: دامنه و برد توابع زیر را مشخص کنید؟
حل ۳:
(1
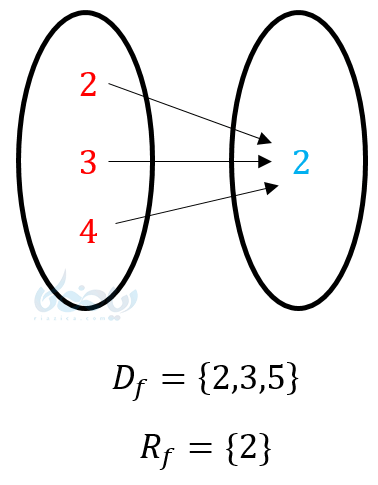
(2
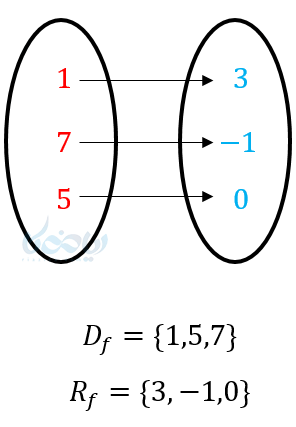
اگر تابع به صورت نمودار باشد، مجموعه تشکیل دهنده \( \Large x \)ها دامنه و مجموعه تشکیل دهنده \( \Large y \)ها برد است.
نکته ۱: کافی است از نمودار به محورها وصل کنیم و محدوده \( \Large x , y \) را مشخص کنید.
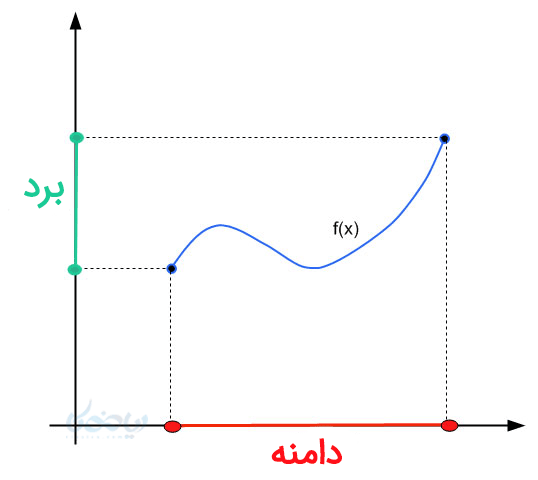
مثال ۴: دامنه و برد توابع زیر را مشخص کنید؟
حل ۴:
(1
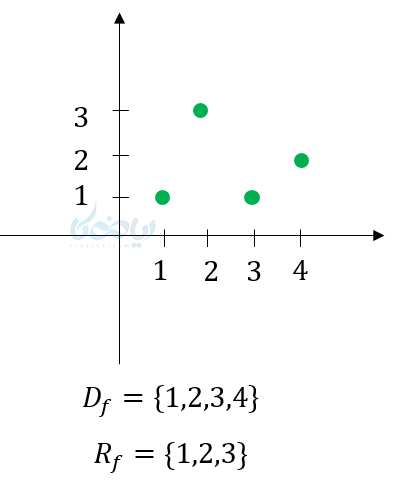
(2
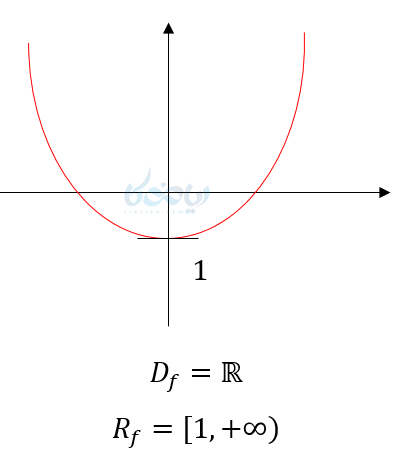
(3
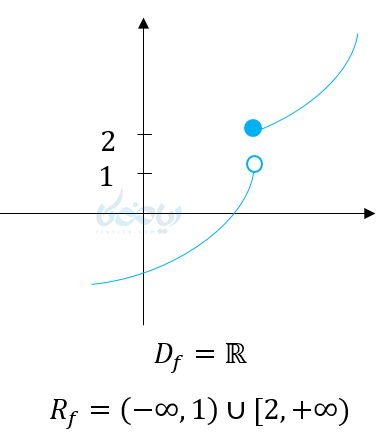
پس داریم:
تعریف دامنه
مجموعه همهٔ مؤلفه‌های اول تشکیل دهنده تابع را دامنه می‌گویند و آن را با \( \Large D \) نمایش می‌دهند. (دامنه تابع \( \Large D_f = f \) )
تعریف برد
مجموعه همهٔ مؤلفه‌های دوم تشکیل دهنده تابع را برد تابع می‌گویند و آن را با \( \Large R \) نمایش می‌دهند. (برد تابع \( \Large R_f = f \) )
مثال ۵: دامنه و برد توابع زیر را بنویسید؟
حل ۵:
(1
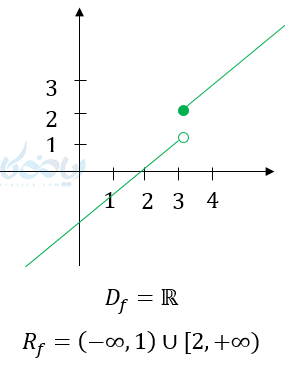
(2
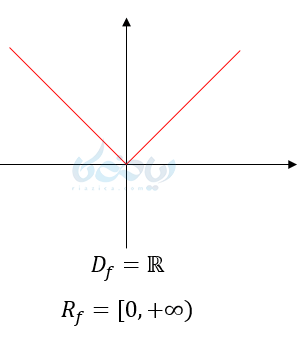
(3
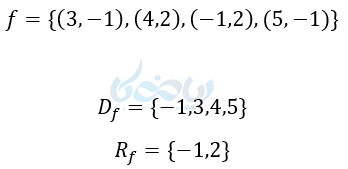
(4
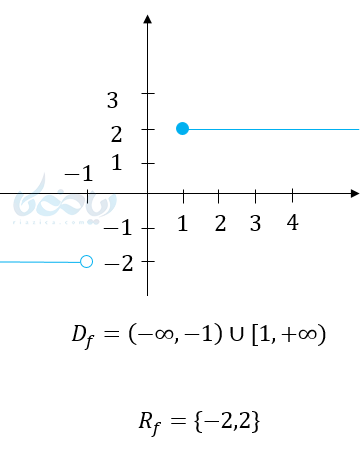
نکته مهم در مورد دامنه توابع
مطلب مهم در مورد دامنه توابع با ضابطه خاص این است که یک تابع فقط به ضابطه‌اش بستگی ندارد. بلکه دامنه تعریف آن هم برای ما مهم است. اگر یک تابع با دامنه های مختلف داده شود، این توابع با هم یکسان نیستند و نمودار آن‌ها متفاوت است.
مثال ۶: تابع \( \Large f(x)=3x-2 \) را در نظر بگیرید و آن را با دامنه‌های داده شده رسم کنید.
الف) با دامنه \( \Large \{0,1,2\} \)
ب) با دامنه \( \Large \mathbb{R} \geq 0 \)
ج) با دامنه \( \Large [-1,2] \)
ت) با دامنه \( \Large \mathbb{R} \)
حل ۶:
این یک تابع خطی است (تابع خطی جزء توابع چندجمله‌ای درجه اول است که به صورت \( \Large y=ax+b \) است.) و با دامنه‌های مختلف خواسته شده. پس داریم:
(الف
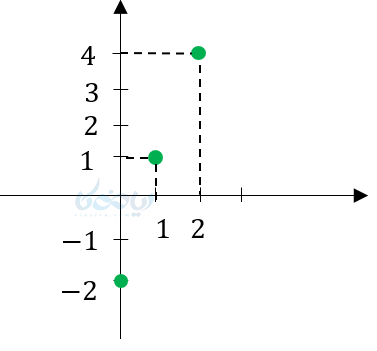
(ب
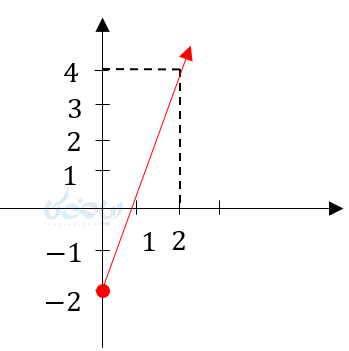
(پ
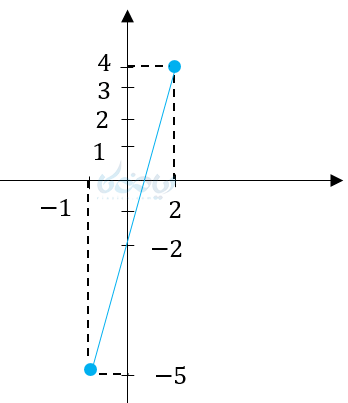
(ت
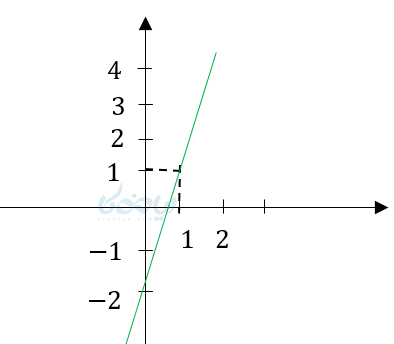
در قسمت الف از یک خط سه نقطه‌اش مدنظر است در قسمت ب یک نیم‌خط داریم در قسمت پ یک پاره‌خط داریم و در قسمت ت یک خط کامل
نکته ۲: اگر در مسئله‌ای ضابطه تابع داده شد اما در مورد دامنه صحبتی نشد بزرگترین دامنه ممکن آن تابع را در نظر می‌گیریم.
بزرگترین دامنه ممکن یک تابع مقادیری است که به جای \( \Large x \) می‌توان قرار داد و تابع به ازای آن مقادیر تعریف شده باشد.
در مورد توابع خطی بزرگترین دامنه ممکن آن‌ها مجموعه اعداد حقیقی \( \Large \mathbb{R} \) میباشد.
مثال ۷: دامنه تابع \( \Large y = \sqrt x \) را پیدا کنید؟
حل ۷: چون زیر تابع با فرجه زوج، عدد منفی بی‌معنی است. پس دامنه این تابع \( \Large D_f=[0,+\infty) \) است. پس بزرگترین دامنه ممکن اعداد حقیقی نا‌منفی است.
در پست تابع گویا در مورد دامنه تابع گویا مفصل صحبت کرد هایم
مقدار تابع
تابع \( \Large f=\{(2,3),(5,7),(-1,4)\} \) را در نظر بگیرید. همانطورکه مشاهده می‌کنید عضو 2 از دامنه به 3 از برد و عضو 5 از دامنه به 7 از برد و عضو 1- از دامنه به 4 از برد نظیر شده است. این مطلب را می‌توان به شکل ساده‌تری بیان کرد:
عضو 2 از دامنه به 3 از برد نظیر شده است.
\( \LARGE f(2)=3 \)
می‌خوانیم \( \Large f \)، دو مساوی سه.
عضو 5 از دامنه به 7 از برد نظیر شده است.
\( \LARGE f(5)=7 \)
و به طور کلی می‌گوییم در تابع \( \Large f \) داریم:
\( \LARGE f(x)=y \)
حال تابع خطی \( \Large y=3x-2 \) را در نظر بگیرید. در واقع داریم \( \Large f(x)=3x-2 \) در این تابع ورودی‌ها \( \Large x \)ها هستند. یعنی ما به \( \Large x \) مقدار می‌دهیم و خروجی‌ها \( \Large y \)ها هستند. حال اگر به این تابع 2 بدهیم به ما 4 تحویل می‌دهد. یعنی:
(1
\( \LARGE f(2)=4 \)
(2
\( \LARGE f(-1)=-5 \)
(3
\( \LARGE f(0)=-2 \)
(4
\( \LARGE f(a)=3a-2 \)
(5
\( \LARGE f(\sqrt 5)=3\sqrt 5 -2 \)
(6
\( \LARGE f(x^2)=3x^2-2 \)
یعنی هر مقداری به تابع بدهیم آن را به جای \( \Large x \) قرار داده عملیات تابع را روی آن اعمال می‌کند و به ما \( \Large y \) تحویل می‌دهد.
مانند یک کارخانه ریسندگی که ماشین آلات رسیندگی در آن وجود دارد. اگر به کارخانه نخ قرمز تحویل دهید پارچه قرمز تحویل می‌گیرید و غیره. برای همین تابع به عنوان یک ماشین تولید \( \Large y \) هم محسوب میشود. برای همین به تابع \( \Large function \) یعنی عملکرد یا کار یا تابع گفته میشود و حرف \( \Large f \) برای نمایش تابع از این کلمه گرفته شده است.
مثال ۸: اگر تابعی به صورت \( \Large f(x)=-4x-1 \) باشد و دامنه آن \( \Large A=\{0,-1,2,4\} \) باشد برد تابع \( \Large f \) را بدست آورید.
حل ۸:
(1
\( \LARGE f(0)=-1 \)
(2
\( \LARGE f(2)=-9 \)
(3
\( \LARGE f(-1)=3 \)
(4
\( \LARGE f(4)=-17 \)
\( \LARGE R_f=\{-1,-9,3,-17\} \)
ویدیو دامنه وبرد تابع
در این ویدیو یک مثال از تعیین برد تابع برای شما آورده شده است
آخر کلاس امروز: آموزش دامنه و برد تابع در ریاضی دهم
مبحث پیدا کردن دامنه و برد تابع مطلب وسیعی است ولی جان کلام، آموزش این مبحث در بالا به صورت کاملا مفهومی به شما نشان داده شده. نمونه سوال ریاضی دهم از این بخش را از ما بپرسید و زیر این پست در قسمت دیدگاه برایمان کامنت کنید. گروه آموزشی ریاضیکا به سوال‌هایتان پاسخ می‌دهند.
ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی دهم به شما پیشنهاد می‌دهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکل‌ها 📒📉
- دامنه و برد تابع به زبان عکس‌ها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!
سلام ممنون از آموزش های خوبتون
واقعا منی که تو درس تابع کلی اشکال داشتم الان کامل یاد گرفتم
ضمن عرض سلام. خداروشکر که آموزش‌ها براتون مفید بودن.
موفق و پیروز باشید
عالی بود?
تشکر بابت انرژی مثبت
خوشحالیم که براتون مفیده بوده
تورابطه تابع چطور میتونیم xوyرو بدست بیاریم؟
سلام و عرض ادب
سوالتون واضح نیست. لطفا کامل تر بنویسید. منظروتون تابع در چه شکلی است؟ (نمودار یا معادله)
موفق باشید.
با سلام خسته نباشید دمدون گرم واقعا سایت خوبی دارین خدا خیرتون
با سلام ممنون از نظر ونگاه شما
عالی بود.
من دبیر ریاضی هستم و از این قسمت برای تدریسم خیلی ایده گرفتم
سلام همکار عزیز.
خیلی خوشحال شدم که این مطالب براتون مفید واقع شده.
انشالله معرف سایت ما به دانش‌آموزانتون باشید.
عالیه ممنون???
سلام و عرض ادب
ممنون از پیام پر مهرتون
موفق باشید
سلام اگه دامنه بدن f(X),هم بدن چجوری باید برد رو پیدا کنم؟؟
با سلام وعرض احترام
بستگی داره چه تابعی باشه ولی اگه امکان داره نمودار تابع رو بکشید واز روی نمودار برد رو پیدا کنید
تابع فقط این نیست که بجای x بزاری y همان برد بیاد توابع پیچیده هستن دامنه وبردشان نیاز به تجزیه دار ودارای شر شروط هستن که به این سادگی هم نیستن
با سلام وعرض ادب
در حد ریاضی دهم مطلب کامل هست در توابع پیچیده تر که فقط ضابطه تابع در دست میباشد کاهی پیدا کردن برد مشکل هست
سلام
برد تابع رادیکال x که دامنه ۰و۹ میشه ۰و ۹ یا R
سلام
برد تابع رادیکال x که دامنه ۰و۹ میشه ۰و ۹ یا R
سلام وعرض احترام
میشود از ۰ تا ۳
سلام ببخشید من توی پیدا کردن دامنه مشکلی ندارم ولی در پیدا کردن برد توابع چرا
هرکاری هم که می کنم بازم به مشکل می خورم فقط کافیه که نموداری که بمون می دن یکم پیچیده شه ده بیا درساش کن
شما راه حلی ندارین؟
که مثلا وقتی می خوام برد رو پیدا کنم یک سری موارد رو در نظر بگیرم؟
با سلاموعرض ادب
منظورتون از روی نمودار هست ؟
سلام
من پروفسور حسابی هستم. انیشتین و هاوکینگ هم اینجا کنار من هستند. ما هر سه تامون خیلی تو این مبحث داغون بودیم. آموزشاتون عالی بود و ما کاملا متحول شدیم.اونقدر که به چندین نظریه جدید دست پیدا کردیم. فقط لطف کنین یکم نظرات و تشکرات تابلو رو کاهش بدین.
با سلام واحترام
پروفسور عزیز ودوستان چه کنیم که دوستان به ما لطف دارن بهشون میگم دیگه تشکر نکنن خاطر جنابعالی مکدر نشه
ممنون خیلی واضح تدریس شده
همینو کتاب درسی دور سرش پیچونده
با سلام وعرض احترام
خوشجالیم که مفید واقع شده
اگه سهمی زیر رادیکال باشه دامنه اشو چجوری بدست میاریم؟
با سلام
کافیه زیر رادیکال رو بزرگتر مساوی صفر بذارید ونامعادله رو از طریق تعیین علامت حل کنید
تابع=رادیکال x
دامنه={0و9}
برد؟
سلام و خسته نباشید
برد این تابع چجوری حساب میشه بی زحمت توضیح میدید
با سلام وادب
کافیه اعضای دامنه رو به جای ایکس بذارید تا برد بدست بیاد یعنی ۰و۳
سلام استاد
خیلی عالی بود
خدا قوت
خدا حفظتون کنه
با توجه به تجربیات خودم روش تدریستون خیلی ساده و جامع و مفهومی بود
عالی عالی عالی
سلام دوست عزیز
ممنون از نظر کارشناسی شما که باعث دلگرمی ما هست
خیلی عالی و کامل و مفید بود من که متوجه شدم ممنون
ممنون از نظر لطف شما