آموزش ریاضی پایه هفتم
مساحت جانبی و کل ریاضی هفتم 🛢💯 – جوانبشو بسنج!
در درسنامۀ مساحت جانبی و کل ریاضی هفتم ابتدا منظورمان از مساحت جانبی را بیان میکنیم. سپس سراغ مساحت کل رفته و چند مثال حل میکنیم. در انتها نیز گستردۀ منشورهای مختلف را بررسی کرده و آنها را رسم میکنیم. سعی میکنیم با استفاده از رسم شکل و حل مثال، به درک بهتر شما از این مبحث کمک کنیم. برای مطالعۀ این درسنامه لازم است تا با منشور و مفاهیمی مثل وجه و قاعدۀ منشور آشنایی داشته باشد؛ بنابراین حتما پیش از شروع مطالعۀ این درسنامه، درسنامۀ حجم های هندسی ریاضی هفتم را مرور کنید. به اولین قسمت از درسنامۀ مساحت جانبی و مساحت کل ریاضی هفتم توجه کنید.
مساحت جانبی منشور
تعریف مساحت جانبی: به مجموع مساحت تمام وجههای یک منشور، مساحت جانبی منشور میگوییم.
به طور مثال، منشور سه وجهی زیر که قاعدۀ آن مثلث متساوی الاضلاع است در نظر بگیرید:
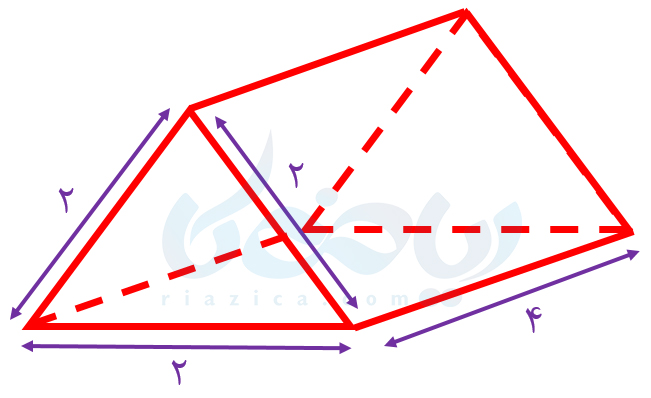
همان طور که میبینید، هر وجه منشور بالا، یک مستطیل با طول \(\Large 4\) و عرض \(\Large 2\) است. بنابراین مساحت هر وجه منشور برابر است با \(\Large 8\). از طرفی منشور داده شده، سه وجه دارد. در نتیجه اگر مساحت جانبی منشور بالا را با \(\Large S\) نشان دهیم، داریم:
\(\LARGE S=3 \times 8=24\)
مثال از درسنامۀ مساحت جانبی و مساحت کل ریاضی هفتم
مثال 1: مساحت جانبی منشور زیر را بیابید.
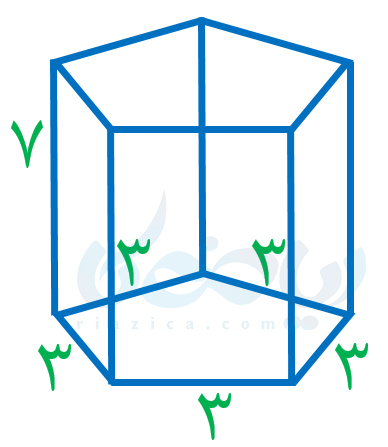
حل: همان طور که در شکل بالا مشخص است، هر وجه منشور، یک مستطیل با طول \(\Large 7\) و عرض \(\Large 3\) است. بنابراین مساحت هر وجه منشور برابر است با \(\Large 21\). از طرفی منشور داده شده، پنج وجه دارد. در نتیجه اگر مساحت جانبی منشور بالا را با \(\Large S\) نسان دهیم، داریم:
\(\LARGE S=5 \times 21=105\)
مساحت جانبی یک منشور را میتوان با استفاده از روش دیگری نیز محاسبه کرد. در قسمت بعدی از درسنامۀ مساحت جانبی و مساحت کل ریاضی هفتم به معرفی این روش میپردازیم.
غلتاندن منشور و یافتن مساحت جانبی
در این قسمت، قصد داریم روش دیگری برای محاسبۀ مساحت جانبی یک منشور معرفی کنیم.در دو مثال بالا قاعده منشورها شکلهای منتظم بودن ولی در شکل زیر قاعده یک مثلث مختلف الاضلاع است پس وجه های منشور با هم برابر نیستند.
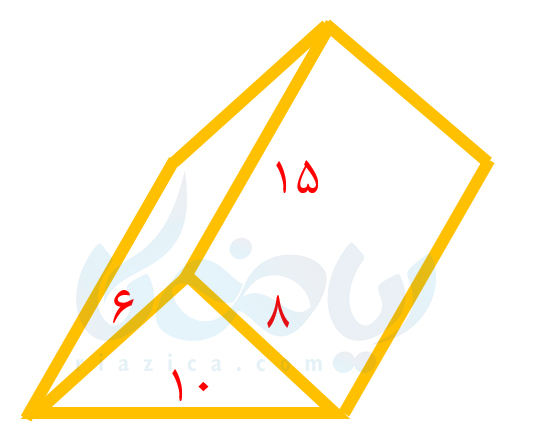
برای محاسبۀ مساحت جانبی منشور بالا میتوانیم مساحت هر وجه آن را به دست آورده و آنها را با یکدیگر جمع کنیم. در این صورت مساحت جانبی منشور داده شده برابر است با:
\(\Large S=15 \times 6+15 \times 8+15 \times 10\)
\(\LARGE =90+120+150\)
\(\LARGE =360\)
بیایید کمی خلاقیت به خرج دهیم! منشور را به صورت زیر روی یک کاغذ غلتانده و هر وجه را رسم میکنیم:
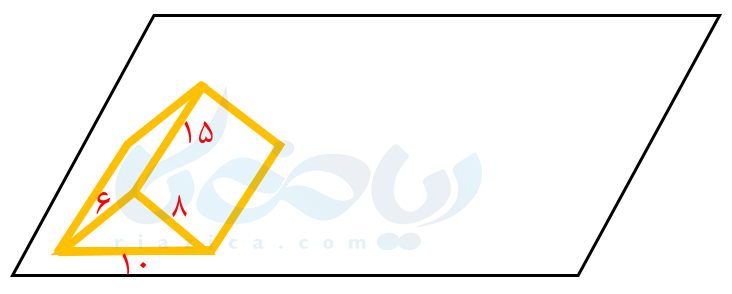
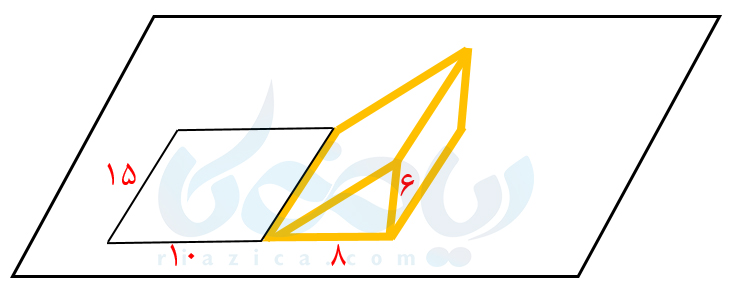
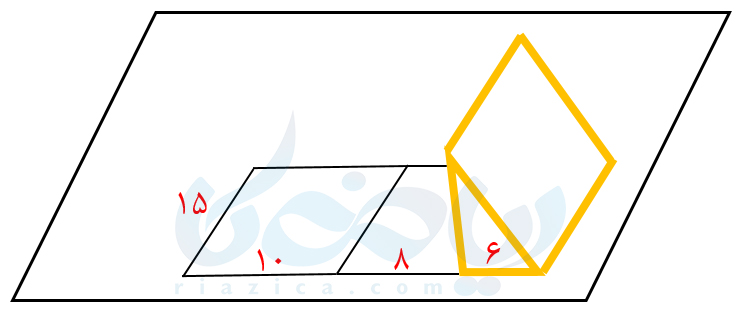
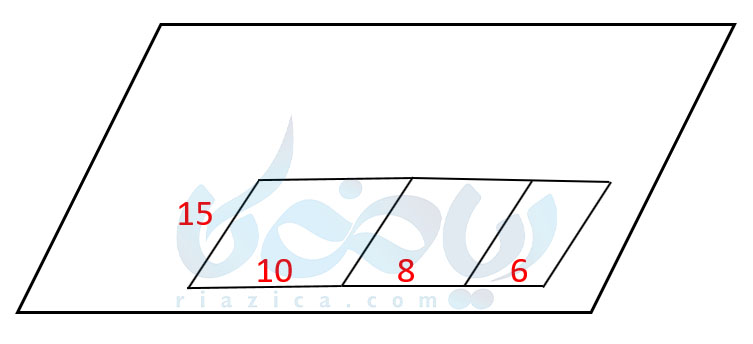
مساحت جانبی منشور برابر است با مجموع مساحت مستطیلهای بالا؛ یعنی مساحت جانبی منشور برابر است با مساحت مستطیل بزرگ. حال کمی دقت کنید! طول مستطیل بزرگ برابر است با محیط قاعدۀ منشور. عرض مستطیل بزرگ برابر است با فاصلۀ دو قاعدۀ منشور که به آن ارتفاع منشور میگوییم. بنابراین مساحت جانبی منشور برابر است با حاصل ضرب محیط قاعدۀ منشور در ارتفاع آن. رابطۀ بسیار جالبی به دست آوردیم. از این رابطه میتوانیم برای محاسبۀ مساحت جانبی منشورهای دیگر نیز استفاده کنیم. یعنی اگر محیط قاعدۀ یک منشور را با \(\Large P\) و ارتفاع آن را با \(\Large h\) نشان دهیم، پس محاسبه مساحت جانبی هر نوع منشوری از رابطۀ کلی زیر به دست میآید:
\(\LARGE S=P \times h\)
در این مثال، محیط قاعدۀ منشور و ارتفاع آن برابر بود با:
\(\LARGE P=6+8+10=24\)
\(\LARGE h=15\)
در نتیجه مساحت جانبی منشور برابر است با:
\(\LARGE S=P \times h\)
\(\LARGE =24 \times 15\)
\(\LARGE =360\)
برای علاقهمندان: در این منشور، ارتفاع منشور با یال آن برابر بود. اما در همۀ منشورها لزوماً این چنین نیست. در صورتی که مایلید در مورد منشورهای مایل مطالعه کنید.
به قسمت بعدی از درسنامۀ مساحت جانبی و مساحت کل ریاضی هفتم توجه کنید.
غلتاندن استوانه به عنوان یک منشور
از آنجاییکه استوانه نیز یک منشور است، میتوانیم کاری را که در قسمت قبل برای یک منشور سه وجهی انجام دادیم، برای استوانه نیز انجام دهیم؛ یعنی استوانه را روی یک صفحه غلتانده و مساحت جانبی آن را به دست آوریم. استوانهٔ زیر را در نظر بگیرید:

اگر استوانه را روی یک صفحه بغلتانیم، شکلهای زیر به دست میآیند:

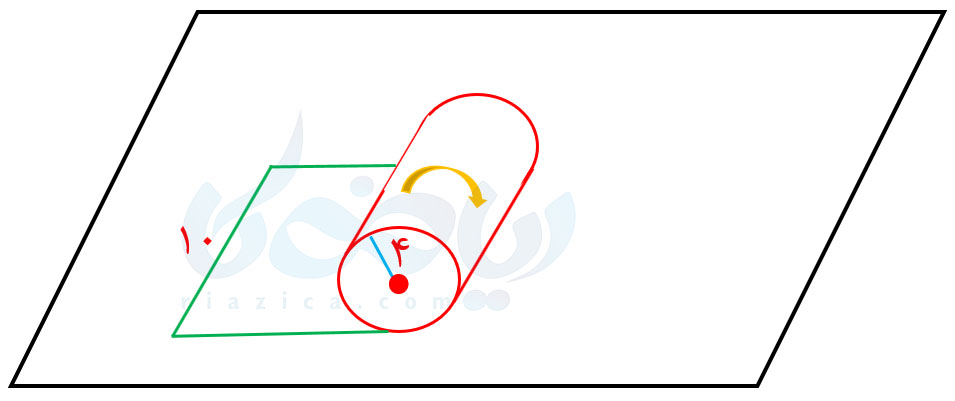
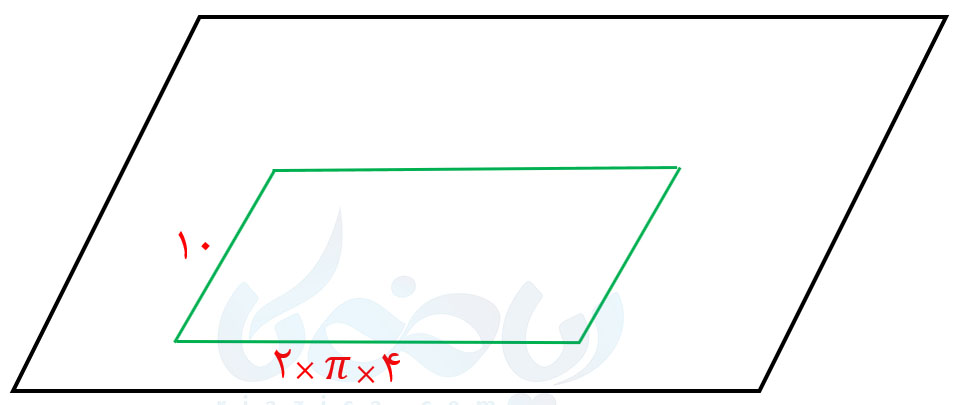
همان طور که میبینید، مساحت جانبی استوانه برابر است با مساحت مستطیل شکل آخر که عرض آن برابر با ارتفاع استوانه و طول آن برابر با محیط دایرهاست. بنابراین مساحت جانبی استوانه برابر است با:
\(\LARGE S=2 \times \pi \times 4 \times 10 \)
\(\LARGE \Rightarrow S=80 \pi \)
مثال از درسنامۀ مساحت جانبی و مساحت کل ریاضی هفتم
مثال 2: غلتکها، اجسام استوانهای شکل هستند که برای صاف کردن زمین و کاربردهای دیگر به کار میروند. اگر شعاع استوانۀ یک غلتک، \(\Large 1\) متر و ارتفاع استوانۀ آن \(\Large 3\) متر باشد، با \(\Large 4\) بار چرخاندن آن، چند متر زمین صاف میشود؟ (\(\Large \pi\) را برابر با \(\Large 3\) در نظر بگیرید)

حل: وقتی غلتک را روی زمین میچرخانیم، به ازای هر بار چرخش، به اندازۀ مساحت جانبی غلتک، زمین صاف میشود. در نتیجه برای محاسبۀ مساحت زمینی که صاف میشود کافی است مساحت جانبی غلتک را به دست آورده و در \(\Large 4\) ضرب کنیم. برای به دست آوردن مساحت جانبی از رابطۀ قسمت قبل استفاده میکنیم؛ یعنی محیط قاعدۀ استوانه را در ارتفاع آن ضرب میکنیم. اگر ارتفاع استوانه را با \(\Large h\)، محیط آن را با \(\Large P\) و مساحت جانبی آن را با \(\Large S\) نشان دهیم، داریم:
\(\LARGE P=2 \pi r= 2 \times 3 \times 1=6\)
\(\LARGE h=3\)
\(\LARGE S=P \times h=6 \times 3=18\)
کل مساحت زمینی که صاف شده برابر است با \(\Large 4\) برابر مساحت جانبی استوانه، یعنی \(\Large 72\) سانتی متر مربع.
مساحت کل منشور
تعریف مساحت کل: به مجموع مساحت جانبی و مساحت دو قاعدهٔ منشور، مساحت کل منشور میگوییم.
بنابراین، برای محاسبۀ مساحت کل یک منشور، کافی است ابتدا با استفاده از آنچه در این درسنامه آموختیم، مساحت جانبی را به دست آورده و سپس با مساحت دو قاعدۀ منشور جمع کنیم. برای اینکه بهتر متوجه شوید، به مثالهای بعدی توجه کنید.
مثال از درسنامۀ مساحت جانبی و مساحت کل ریاضی هفتم
مثال 3: مساحت کل منشور زیر را به دست آورید.
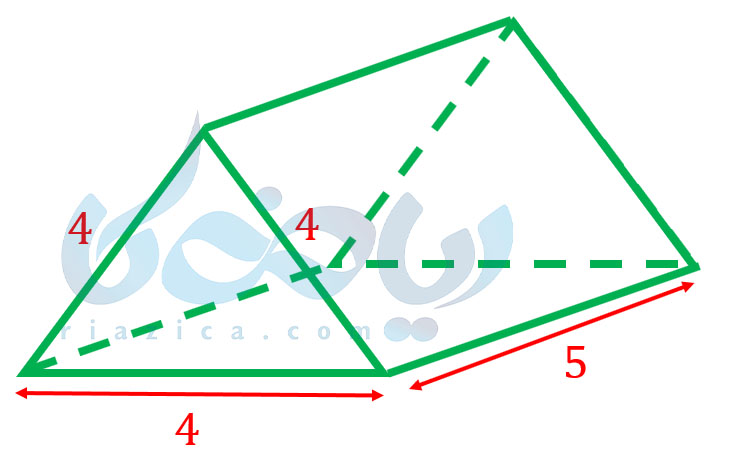
حل: همان طور که گفتیم، مساحت کل یک منشور برابر است با مجموع مساحت جانبی و مساحت دو قاعدۀ منشور. برای به دست آوردن مساحت جانبی، کافی است محیط قاعدۀ منشور را به دست آورده و در ارتفاع آن ضرب کنیم. محیط قاعدۀ منشور برابر است با مجموع اضلاع مثلث؛ از آنجا که مثلث متساوی الاضلاع است، محیط قاعدۀ منشور برابر است با سه برابر ضلع آن، بعنی \(\Large 12\). اگر مساحت جانبی منشور را با \(\Large S_L\) نشان دهیم، داریم:
\(\LARGE S_L=P \times h=12 \times 5=60\)
حال باید مجموع مساحت قاعدههای منشور را به دست آوریم. برای این کار کافی است مساحت یک قاعده را به دست آورده و در دو ضرب کنیم. برای به دست آوردن مساحت قاعده ابتدا باید اندازهٔ ارتفاع مثلث را به دست آوریم. با توجه به اینکه در مثلث متساوی الاضلاع، ارتفاع مثلث، میانهٔ آن نیز هست (اگر دلیل آن را نمیدانید، سعی کنید با استفاده از همنهشتی مثلثها آن را ثابت کنید)، میتوانیم شکل زیر را رسم میکنیم:
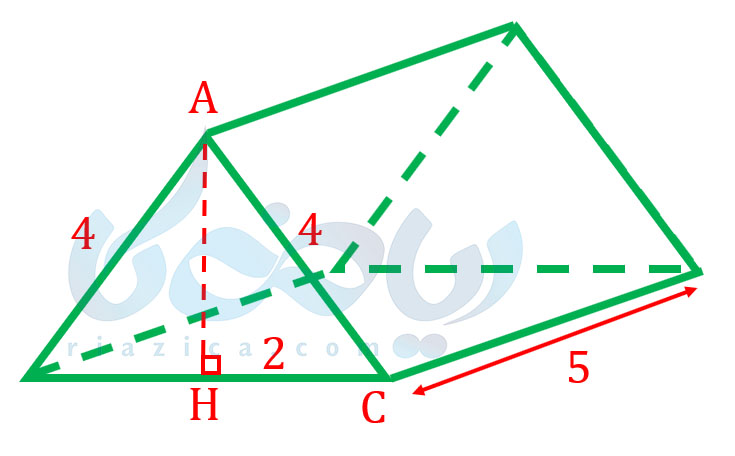
کافی است رابطهٔ فیثاغورس را در مثلث \(\Large AHC\) بنویسیم:
\(\LARGE AH^2+HC^2=AC^2\)
\(\LARGE \Rightarrow AH^2+4=16\)
\(\LARGE \Rightarrow AH^2=12\)
\(\LARGE \Rightarrow AH=\sqrt{12}=2\sqrt{3}\)
بنابراین، اندازهٔ ارتفاع مثلث قاعده برابر است با \(\Large 2 \sqrt{3}\). حال کافی است قاعدهٔ مثلث را در ارتفاع آن ضرب کرده و سپس حاصل را در \(\Large 2\) ضرب کنیم تا مساحت مجموع دو قاعده به دست بیاید. اگر مجموع مساحت قاعدههای منشور را با \(\Large S_B\) نشان دهیم، داریم:
\(\LARGE S_B=2 \times (\frac{4 \times 2 \sqrt{3}}{2})=8 \sqrt{3}\)
برای محاسبۀ مساحت کل منشور کافی است مساحت جانبی و مجموع مساحت دو قاعده را با هم جمع کنیم. اگر مساحت کل را با \(\Large S_T\) نشان دهیم، داریم:
\(\LARGE S_T=S_L+S_B=60+8 \sqrt{3}\)
به قسمت بعدی از درسنامۀ مساحت جانبی و کل ریاضی هفتم توجه کنید.
فرمول حجم و مساحت جانبی و مساحت کل استوانه
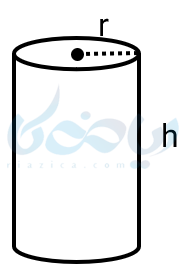
با توجه به مطالب بالا در استوانه ای به شعاع قاعده \(\Large r \) و ارتفاع \(\Large h \) فرمول های حجم و مساحت جانبی و کل استوانه به شکل زیر خواهد بود.
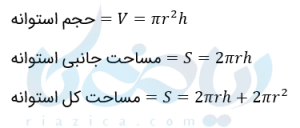
گستردۀ یک منشور
اگر یک استوانۀ کاغذی داشته باشیم، میتوانیم آن را به صورت زیر باز کرده و اصطلاحاً شکل گستردۀ آن را به دست آوریم:
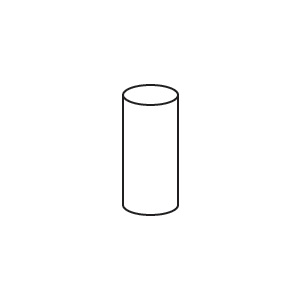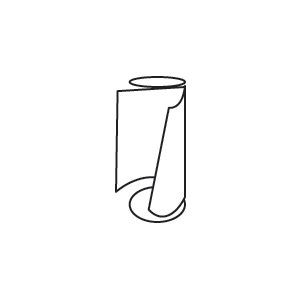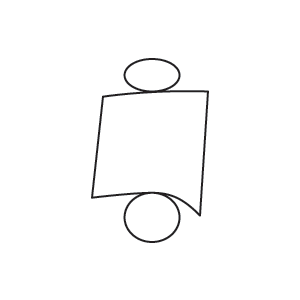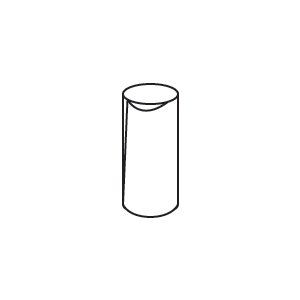
همین کار را میتوانیم برای منشورهای دیگر نیز انجام دهیم. مساحت سطحی که در شکل گسترده داریم، همان مساحت کل منشور است. به مثال بعدی از درسنامۀ مساحت جانبی و کل ریاضی هفتم توجه کنید.
مثال از گستردۀ منشور
مثال 4: گستردۀ یک منشور \(\Large 3\) وجهی و یک منشور \(\Large 5\) وجهی را رسم کنید.
حل: وجههای جانبی یک منشور سه وجهی، مستطیل هستند. و قاعدههای آن نیز مثلث هستند. همچنین در شکل گسترده، از هر قاعده یک ضلع روی وجههای جانبی میافتد. در نتیجه میتوانیم شکل زیر را به عنوان گستردۀ یک منشور سه وجهی رسم کنیم:
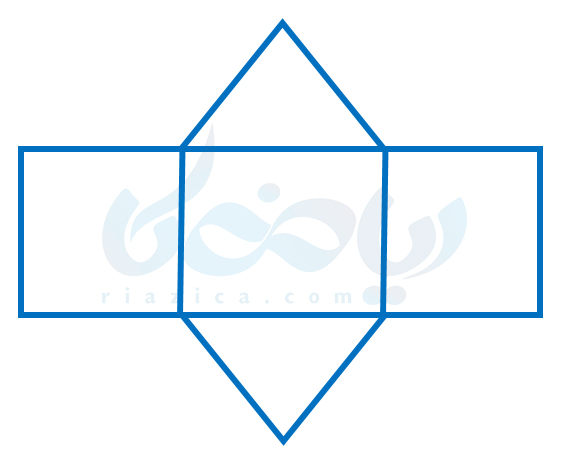
مظابق با توضیحاتی که برای منشور سه وجهی دادیم، میتوانیم شکل زیر را نیز به عنوان گستردۀ منشور پنج وجهی در نظر بگیریم:
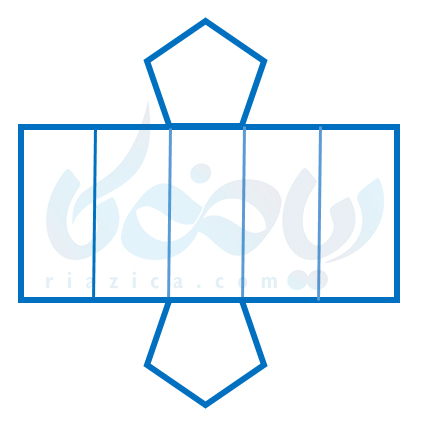
در ادامه پست حجم وسطح ریاضی هفتم را مطالعه کنید.
زنگ آخر کلاس مساحت جانبی و کل ریاضی هفتم
در درسنامهای که از ریاضی هفتم خواندیم، روش به دست آوردن مساحت جانبی و مساحت کل منشور را بیان کردیم. همان طور که دیدید، برای به دست آوردن مساحت جانبی منشور کافی بود محیط قاعدۀ آن را در ارتفاع ضرب کنیم. برای به دست آوردن مساحت کل منشور نیز باید مساحت جانبی را با مجموع مساحت دو قاعدۀ منشور جمع میکردیم. در انتهای درسنامه نیز، به بررسی گستردۀ یک منشور پرداختیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با معادله خط ریاضی نهم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





ممنونم. خیلی عالی بود.
با سلام وعرض احترام
ممنون از نگاه پر مهر شما
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
ممنون خیلی عالیه
با سلام وادب
ممنون از شما دوست عزیز
عالی بود خیلی آموزنده بود
ممنون از نظر محبت آمیز شما
عالیی بود
واقعا که جای بعضی از دبیرا اصلا تو آموزش پرورش نیست مثل معلم ما
۲ کلمه میگه ۱ هفته نشده امتحان میگیره
اصلا به کتاب نگاه نمیکنه
کلاس هم که از بس معلممون ببخشید ولی خنگه معاون میاد تو کلاس
متاسفم برای آموزش وپرورش برای استخدام معلم های مفت خور
سلام دوست عزیز
در همه اقشار آدم وظیف شناس وغیر موظف هست اکثر معلمان دلسوز هستن ولی گاهی متاسفانه معلم وظیفه نشناس هم پیدا میشه
من چندتا سوال دارم ؟
خیلی بده
سلام دوست عزیز
کاش نطرتون رو دقیق تر بیان کنید تا بدانیم کجای کار اشکال داره
مکعب نیست????
مکعب جزو منشورهاست این پست رو مطالعه کنیدhttps://riazica.com/volume-of-a-prism/
عااالی
سلام من اصلا نفهمیدم و اصلا در رابطه با ریاضی هفتم نبود متاسفم خیلی بد بود🙁اصلا هیج عددی ننوشته بود😞
سلام بله همینطوره
اصلا برای هفتم جزر نداریم
با سلام دوست عزیز اگه کامل بخونید کلی مثال زدیم
عالی بود خدا قوت دستتون درد نکنه
با سلام واحترام
ممنون از توجه شما
ببخشید من رادیکال رو در اونجا نفهمیدم مگه به دست اوردن مساحت هم اینقدرکار داره ؟؟؟؟؟ میشه راهنمایی کنید
با سلام وادب
برای مساحت کل مساحت قاعده رو که مثلث هست میخواهی چون ارتفاع مثلث رو نداریم باید ابتدا ارتفاع رو از رابطه فیثاغورس بدست بیاریم چند بار با دقت بخوانید متوجه میشید
عالی حرف ندارن
ممنون که وقت گذاشتین
با سلام
ممنون از نظر ونگاه شما
سلام ببخشید فرمول مساحت کل و جانبی چیه
سلام
مساحت کل وجانبی چه شکلی ؟
ممنون از تدریس عالی شما
سلام دوست عزیز متن رو بخونید به جواب میرسید.
ممنون از لطف شما
با سلام ودرود
ممنون از انرژی شما
با سلام و تشکر. عالی بود.
با سلام دوست عزیز
خرسندیم که مفید بوده
عالی بود ❤
با سلام وادب
ممنون از نگاه شما
خیلی خوب بود.شما خیلی خوبید.¿¡
با سلام وادب
ممنون شما هم خوبید
خیلی خیلی عالی بود ممنون از زحمات شما
با سلام دوست عزیز
ممنون از محبت شما
من متوجه نشدم😭😭
در مسائل چه مواقی باید مساحت جانبی و چه مواقعی باید مساحت کل رو به دست بیاریم؟!
با سلام وادب
گاهی مستقیم سوال میگه کدوم وگاهی از روی صورت مسئله باید فهمید مثلا میگه دیواره استوانه ای را میخواهیم رنگ بزنیم این یعنی مساحت جانبی یا همون بدنه یا مثلا میگه یه مکعب رو با کاغذ کادو کلش رو بپوشانیم این میشه مساحت کل
عالی بود
عالی
عالی بود من خیلی خوب یاد گرفتم
با تشکر 🌹🌹
با سلام
خدا رو شکر
سلام خیلی ممنون واقعا کاربردی بود فقط معلم های ما رادیکال رو توضیح ندادن و توی کتاب نیست که یاد بگیریم همه ی مبحث رو متوجه شدم به جز اون قسمت ممنون میشم اون قسمت رو حذف کنین تا کیفیت سایت بره بالا تر
سلام دوست عزیز
ممنون از نظر شما وقتی امسال رادیکال رو بخونید اونها هم به کارتون میاد
عالی بود بسیار خوب بود من رازی بودم از این همه توضیح خوب و اینکه ای کاش مطالب بیشتری را به نمایش میگذاشتین برای ما باز هم ممنونم از لطفتون چون من الان نیاز داشتم به تمام نکات ریاضی
سلام دوست عزیز
ما کل پایه هفتم رو درس به درس گذاشتیم در سایت