آموزش ریاضی پایه نهم
سطح و حجم ریاضی نهم 🎲⚽️ – ۳ بعدی شو ببین!
در درسنامهٔ سطح و حجم ریاضی نهم به بررسی موارد زیر میپردازیم:
- گستردهٔ حجمهای هندسی و مساحت آنها
- دوران یک شکل و به دست آوردن حجم
- برش یک شکل با یک صفحه
سعی میکنیم با حل مثال و رسم شکلهای مختلف، به درک بهتر شما از این مبحث کمک کنیم. با ما تا انتهای درسنامهٔ سطح و حجم ریاضی نهم همراه باشید.
گستردهٔ مکعب و مکعب مستطیل
گستردهٔ یک مکعب یا یک مکعب مستطیل را میتوان به روشهای مختلفی نشان داد. در شکل زیر یک مکعب به همراه گستردهٔ آن را مشاهده میکنید. همان طور که میبینید، اندازهٔ تمام اضلاع (یالها)، هم در مکعب و هم در گستردهٔ آن برابر با \(\Large a\) است.
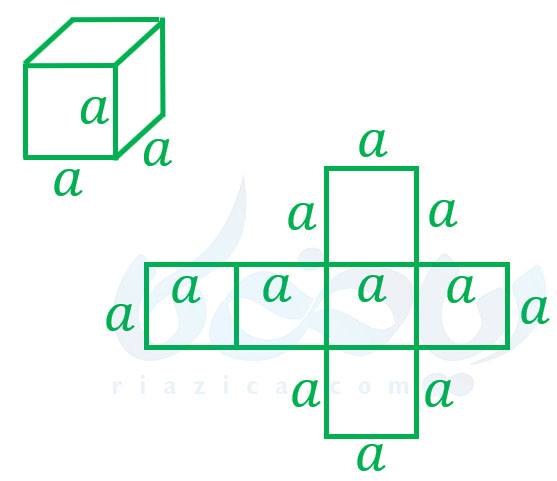
در شکل زیر نیز میتوانید یک مکعب مستطیل به همراه گستردهٔ آن را مشاهده کنید. ابعاد گسترده، مطابق با ابعاد مکعب مستطیل، روی شکل مشخص شدهاند.
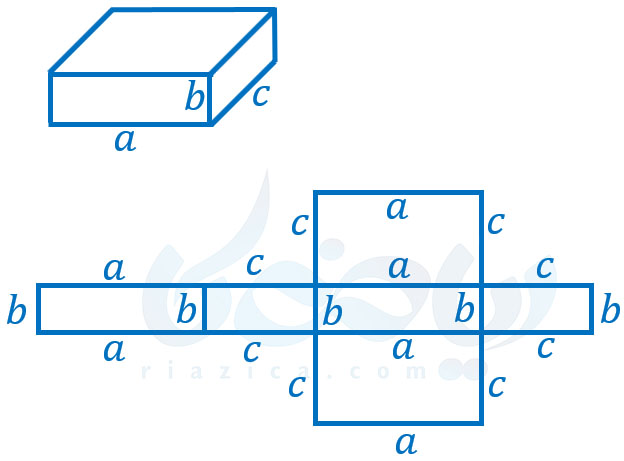
به قسمت بعدی از درسنامهٔ سطح و حجم ریاضی نهم توجه کنید.
گستردهٔ هرم
همان کاری را که برای مکعب و مکعب مستطیل انجام دادیم، میتوانیم برای هرم نیز انجام دهیم. در شکل زیر یک هرم با قاعدهٔ مثلث و گشتردهٔ آن را مشاهده میکنید:
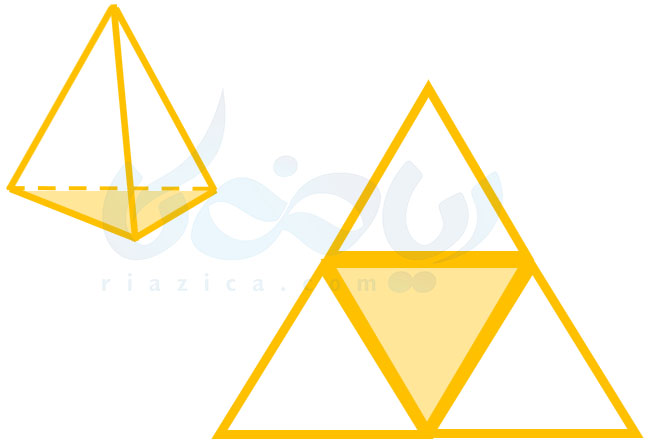
مثال از درسنامهٔ سطح و حجم ریاضی نهم
مثال 1: در شکل زیر یک هرم منتظم با قاعدهٔ مربع مشاهده میکنید. اندازهٔ تمام یالها (پارهخط هایی که از رأس هرم به قاعده متصل هستند) با یکدیگر برابر است. ابتدا شکل گستردهٔ آن را رسم کنید. سپس، مساحت گستردهٔ آن را به دست آورید.
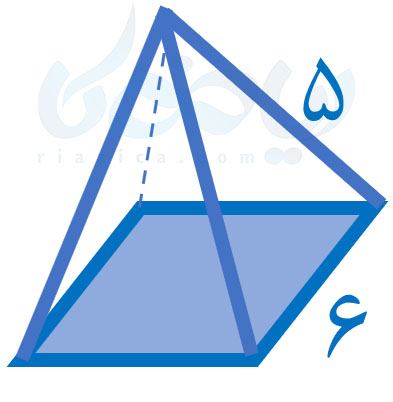
حل: ابتدا گستردهٔ هرم را رسم میکنیم:
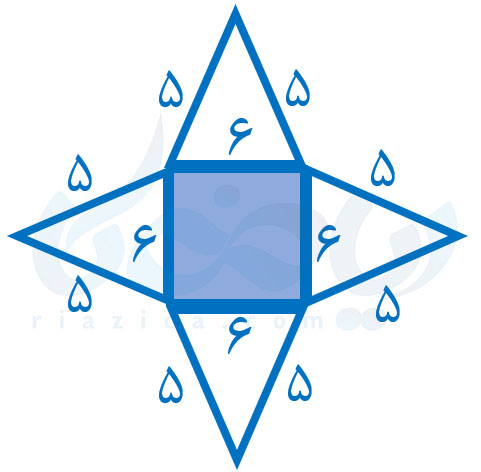
مساحت شکل گستردهٔ هرم از مجموع مساحت مربع و مساحت چهار مثلث کناری به دست میآید. اگر مساحت مربع را با \(\Large S_a\) نشان دهیم، داریم:
\(\LARGE S_a=a^2=6^2=36\)
برای به دست آوردن مجموع مساحت مثلثهای کناری کافی است مساحت یک مثلث را به دست آورده و در \(\Large 4\) ضرب کنیم. قاعدهٔ هر مثلث برابر با \(\Large 6\) است؛ اما ارتفاع هر مثلث را نداریم. بنابراین باید ارتفاع هر مثلث را به دست آوریم. در شکل زیر، یکی از مثلثها را به تنهایی نشان دادهایم:
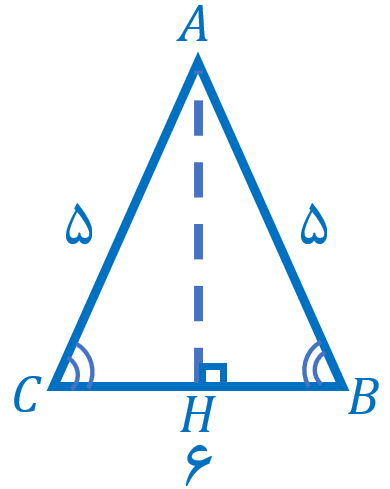
در شکل بالا، مثلثهای \(\Large ABH\) و \(\Large ACH\) به دلیل برابری دو ضلع و زاویهٔ بین، با یکدیگر همنهشت هستند؛ زیرا، \(\Large AB\) با \(\Large AC\) برابر است. همچنین، \(\Large AH\) بین دو مثلث مشترک است. از طرفی، از آنجاییکه زاویهٔ \(\Large B\) با \(\Large C\) و زاویهٔ \(\Large AHB\) با \(\Large AHC\) برابر است، دو زاویهٔ \(\Large BAH\) و \(\Large CAH\) نیز با یکدیگر برابرند. بنابراین، همان طور که گفتیم، دو مثلث \(\Large ABH\) و \(\Large ACH\) با یکدیگر همنهشت هستند و در نتیجه، \(\Large BH\) با \(\Large CH\) نیز برابر است و اندازهٔ هر کدام از آنها برابر است با نصف ضلع مربع، یعنی \(\Large 3\). حال، برای به دست آوردن اندازهٔ \(\Large AH\) کافی است از قضیهٔ فیثاغورس استفاده کنیم:
\(\LARGE AH^2+BH^2=AB^2\)
\(\LARGE \Rightarrow AH^2+3^2=5^2\)
\(\LARGE \Rightarrow AH=4\)
بنابراین، با توجه به اندازهٔ قاعده و ارتفاع مثلث \(\Large ABC\)، مساحت آن به صورت زیر به دست میآید:
\(\LARGE S_{ABC}=\frac{AH \times BC}{2}\)
\(\LARGE \Rightarrow S_{ABC}=\frac{4 \times 6}{2}=12\)
پس، مساحت گستردهٔ هرم که از مجموع مساحت مربع و چهار برابر مساحت یکی از مثلثها به دست میآمد، برابر است با:
\(\LARGE S=S_a+4S_{ABC}\)
\(\LARGE \Rightarrow S=36+48=84\)
به قسمت بعدی از درسنامهٔ سطح و حجم ریاضی نهم توجه کنید.
ساخت مخروط از یک قطاع
میتوان با استفاده از یک قطاع از دایره، یک مخروط به وجود آورد. به تصویر متحرک زیر دقت کنید:
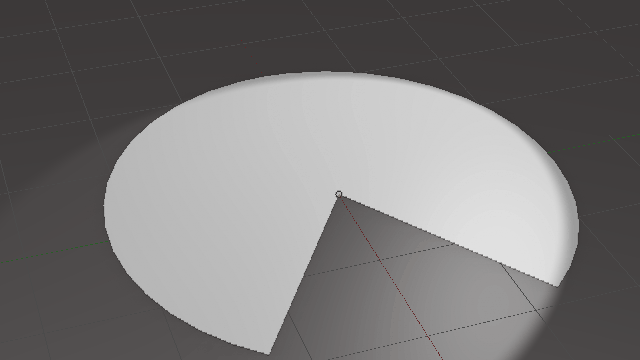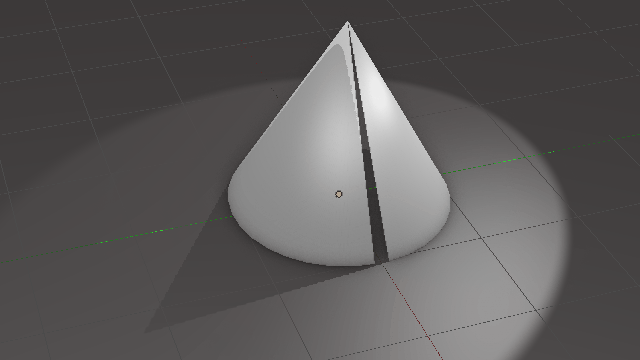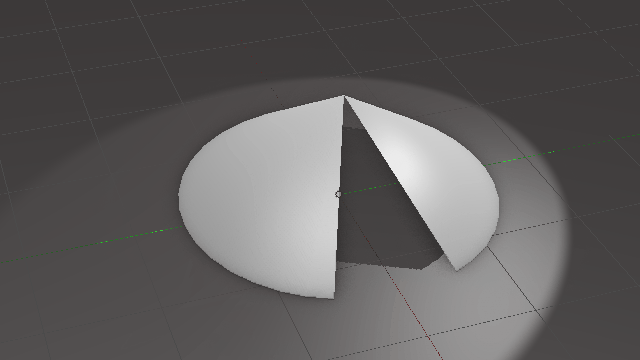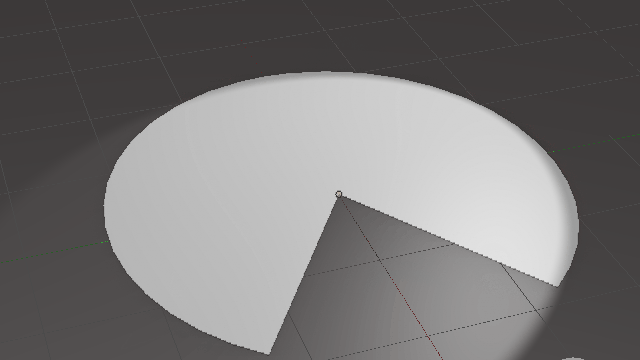
بدیهی است که طول کمان قطاع، برابر است با محیط قاعدهٔ مخروط. مثلاً در شکل زیر، با استفاده از یک قطاع با زاویهٔ \(\Large 240\) درجه، یک مخروط ساختهایم. طول کمان \(\Large AB\) در شکل سمت چپ، برابر است با محیط قاعدهٔ مخروط در شکل سمت راست:
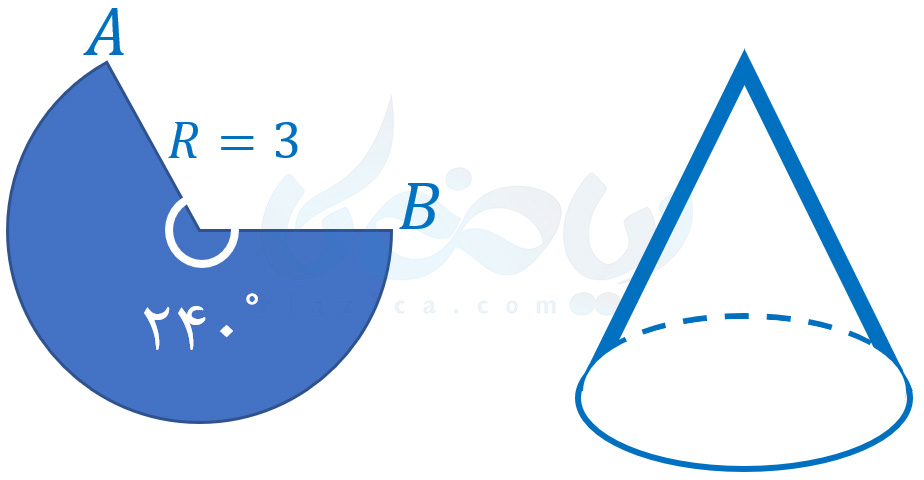
برای به دست آوردن طول کمان \(\Large AB\) که همان محیط قاعدهٔ مخروط نیز هست، کافی است از یک تناسب ساده استفاده کنیم. نسبت طول کمان \(\Large AB\) به محیط کلدایرهای که کمان از آن جدا شده، برابر است با نسبت زاویهٔ قطاع به \(\Large 360\) درجه. یعنی داریم:
\(\LARGE \frac{AB}{2 \pi r}=\frac{240}{360}\)
\(\LARGE \Rightarrow \frac{AB}{2 \pi r}=\frac{2}{3}\)
شعاع دایرهای که کمان از آن جدا شده، برابر با \(\Large 3\) است. بنابراین، در رابطهٔ بالا، به جای \(\Large r\) مقدار \(\Large 3\) را قرار میدهیم. در این صورت داریم:
\(\LARGE \frac{AB}{6 \pi}=\frac{2}{3}\)
\(\LARGE \Rightarrow AB=6 \pi \times \frac{2}{3}\)
\(\LARGE \Rightarrow AB=4 \pi\)
بنابراین، طول کمان \(\Large AB\) که همان اندازهٔ محیط قاعدهٔ مخروط نیز هست، برابر است با \(\Large 4 \pi\). به قسمت بعدی از درسنامهٔ سطح و حجم ریاضی نهم توجه کنید.
دوران مستطیل و ساخت استوانه
ساخت حجمهای مختلف با استفاده از دوران را قبلاً در درسنامهٔ حجم و سطح ریاضی هفتم مشاهده کردهاید. همان طور که در پایهٔ هفتم دیدید، از دوارن مستطیل حول یکی از اضلاعش میتوان استوانه به وجود آورد. به تصویر متحرک زیر دقت کنید:

مثال از درسنامهٔ سطح و حجم ریاضی نهم
مثال 2: یک مستطیل را یکبار حول طول آن (شکل 1) و بار دیگر حول عرض آن (شکل 2) دوران میدهیم. در هر حالت، حجم استوانهای که تشکیل میشود را به دست آورید (مقدار \(\Large \pi\) را برابر با 3 در نظر بگیرید).
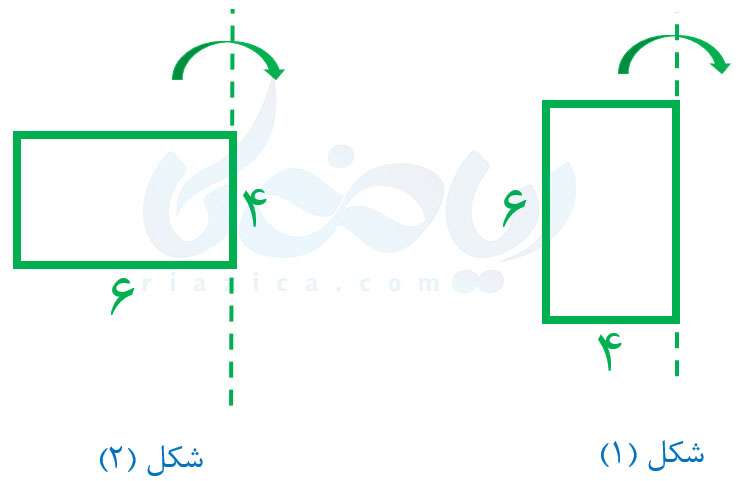
حل: همان طور که در درسنامهٔ محاسبه حجم های منشوری هفتم خواندید، حجم استوانه از حاصل ضرب مساحت قاعده در ارتفاع آن به دست میآید. برای شکل 1، شعاع قاعدهٔ استوانه برابر با عرض مستطیل و ارتفاع استوانه برابر با طول مستطیل خواهد بود. بنابراین حجم استوانهٔ شکل 1 به صورت زیر به دست میآید:
\(\LARGE V_1=\pi R^2h\)
\(\LARGE =3 \times 4^2 \times 6\)
\(\LARGE =288\)
برای شکل 2، شعاع قاعده برابر با طول مستطیل و ارتفاع استوانه برابر با عرض مستطیل خواهد بود. بنابراین حجم استوانهٔ شکل 2 به صورت زیر به دست میآید:
\(\LARGE V_2=\pi R^2h\)
\(\LARGE =3 \times 6^2 \times 4\)
\(\LARGE =432\)
دوران مثلث قائمالزاویه و ساخت مخروط
اگر یک مثلث قائم الزاویه را حول یکی از قاعدههایش دوران دهیم، یک مخروط به دست خواهد آمد. به تصویر متحرک زیر دقت کنید:

مثال از درسنامهٔ سطح و حجم ریاضی نهم
مثال 3: یک مثلث قائمالزاویه را یکبار حول قاعدهٔ کوچک آن (شکل 1) و بار دیگر حول قاعدهٔ بزرگ آن (شکل 2) دوران میدهیم. در هر حالت، حجم مخروطی که تشکیل میشود را به دست آورید (مقدار \(\Large \pi\) را برابر با 3 در نظر بگیرید).
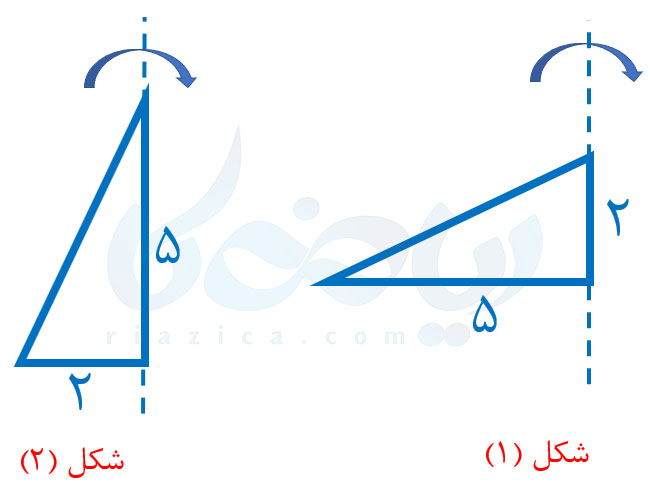
حل: همان طور که در درسنامهٔ حجم هرم و مخروط ریاضی نهم خواندید، حجم مخروط برابر است با \(\Large \frac{1}{3}\) حاصل ضرب مساحت قاعده در ارتفاع. برای شکل 1، شعاع قاعدهٔ مخروط برابر با قاعدهٔ بزرگ مثلث و ارتفاع مخروط برابر با قاعدهٔ کوچک مثلث خواهد بود. بنابراین حجم مخروط شکل 1 به صورت زیر به دست میآید:
\(\LARGE V_1=\frac{1}{3}\pi R^2h\)
\(\LARGE =\frac{1}{3} \times 3 \times 5^2 \times 2\)
\(\LARGE =50\)
برای شکل 2، شعاع قاعدهٔ مخروط برابر با قاعدهٔ کوچک مثلث و ارتفاع مخروط برابر با قاعدهٔ بزرگ مثلث خواهد بود. بنابراین حجم مخروط شکل 2 به صورت زیر به دست میآید:
\(\LARGE V_2=\frac{1}{3}\pi R^2h\)
\(\LARGE =\frac{1}{3} \times 3 \times 2^2 \times 5\)
\(\LARGE =20\)
حجم حاصل از دوران ربع دایره
اگر یک ربعدایره را حول شعاع آن دوران دهیم، یک نیمکره به دست می آید. همچنین اگر یک نیمدایره را حول قطر آن دوران دهیم، کره به دست میآید. به تصویر متحرک زیر دقت کنید:
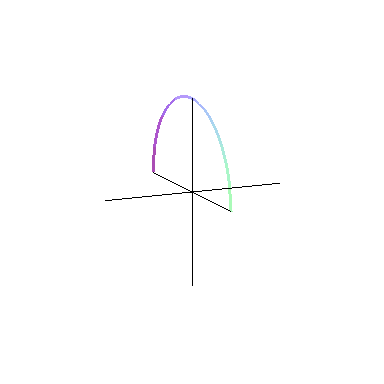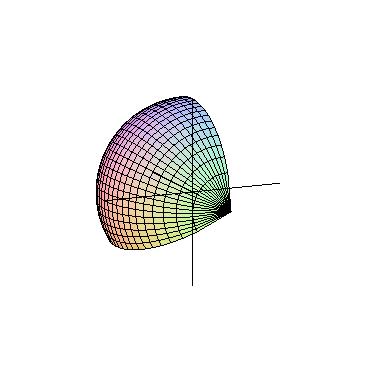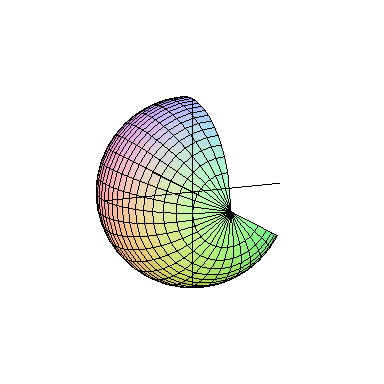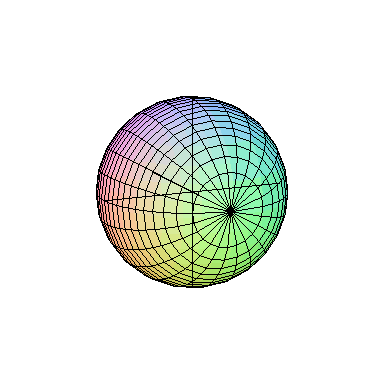
مثال از درسنامهٔ سطح و حجم ریاضی نهم
مثال 4: مطابق شکل زیر، یک ربع دایره را حول شعاع آن دوران میدهیم. حجم شکل حاصل را به دست آورید (مقدار \(\Large \pi\) را برابر با 3 در نظر بگیرید).
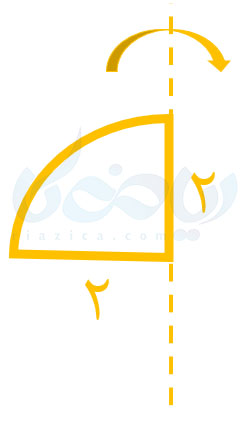
حل: همان طور که در درسنامهٔ حجم و مساحت کره ریاضی نهم خواندید، حجم کره از رابطهٔ \(\Large V=\frac{4}{3} \pi R^3\) به دست میآید. اگر ربعدایرهٔ بالا را حول شعاع آن دوران دهیم، یک نیمکره با شعاع \(\Large 2\) به دست میآید. از آنجا که حجم نیمکره، نصف حجم کره است، داریم:
\(\LARGE V=\frac{1}{2} \times \frac{4}{3} \pi R^3\)
\(\LARGE \Rightarrow V=\frac{1}{2} \times \frac{4}{3} \times 3 \times 2^3\)
\(\LARGE \Rightarrow V=16\)
برش کره
هر حجمی را می توان با یک صفحه برش داد و اصطلاحاً به یک مقطع دست یافت. به طور خاص با مقاطع مخروطی، یعنی شکلهایی که از برش دادن یک مخروط با یک صفحه ایجاد میشوند، در سال دوازدهم آشنا خواهید شد. در درسنامهٔ سطح و حجم ریاضی نهم میخواهیم برش یک کره با یک صفحه را بررسی کنیم. به طور کلی، یک کره و یک صفحه در فضا، یکی از سه حالت زیر را نسبت به یکدیگر دارند:
- صفحه و کره یکدیگر را قطع نمیکنند.
- صفحه و کره یکدیگر را در یک نقطه قطع میکنند؛ در این صورت صفحه بر کره مماس شدهاست.
- صفحه و کره در بیش از یک نقطه یکدیگر را قطع میکنند؛ در این صورت، سطح مقطع یک دایره خواهد بود.
در شکل زیر، حالت سوم، یعنی زمانی که صفحه و کره یکدیگر را در یک دایره قطع میکنند را مشاهده میکنید:
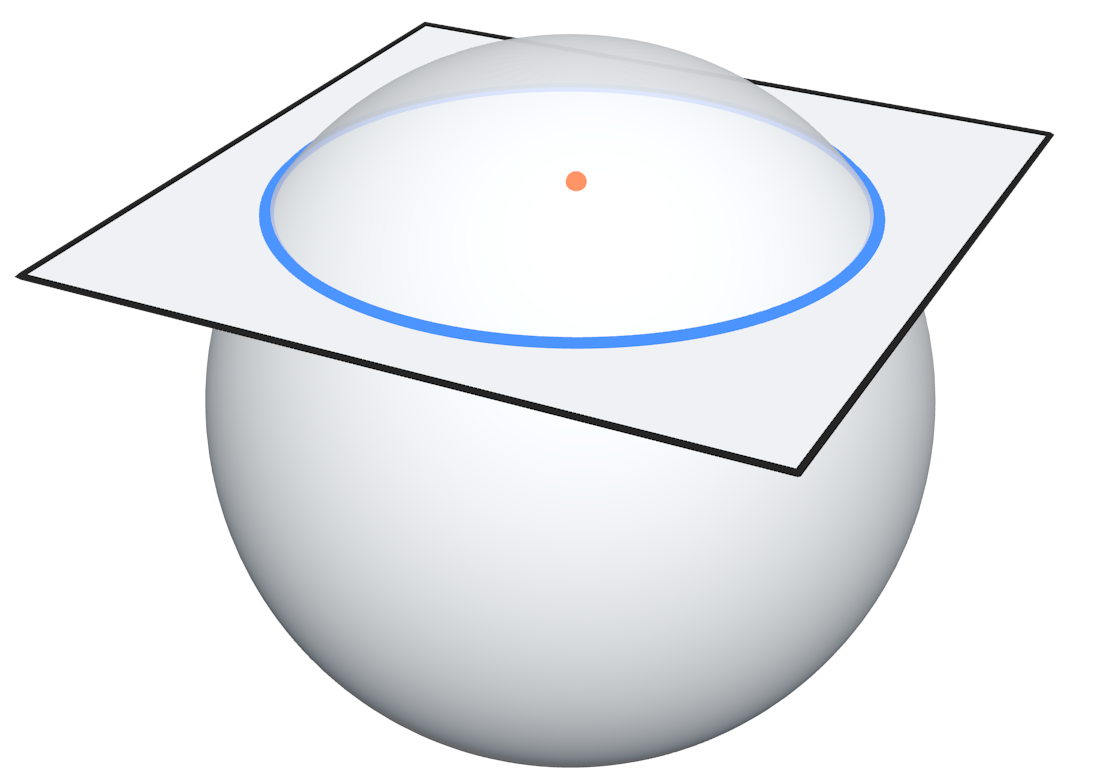
طبیعتاً در صورتی مساحت سطح مقطع بیشترین مقدار ممکن را دارد که یکی از اقطار کره روی صفحه قرار داشته باشد؛ درست مانند شکل یر:
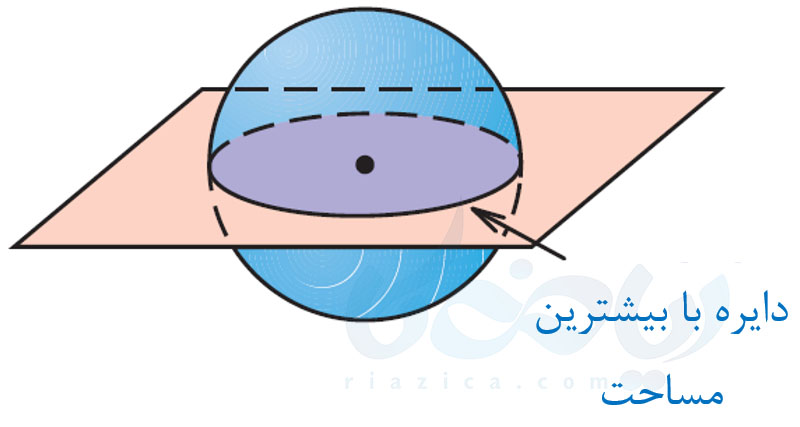
قبل خوندن این پست توصیه میشه پست حجم وسطح ریاضی هفتم رو مطالعه کنید.
زنگ آخر کلاس سطح و حجم ریاضی نهم
در درسنامهای که از ریاضی نهم خواندیم، ابتدا گستردهٔ هرم را بررسی کرده و از آن مثال حل کردیم. سپس، چگونگی ساخت مخروط از یک قطاع دایره را با یکدیگر دیدیم. در انتها نیز، دوران مستطیل، دایره و مثلث قائمالزاویه را بررسی کرده و حجم اَشکال به وجود آمده را محاسبه کردیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با سطح و حجم ریاضی نهم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





کامل وجامع
با سلام ممنون از نگاه شما