تقسیم و بخش پذیری حسابان 2 ➗🔱 – جادویی یادبگیر!

در درسنامهٔ تقسیم و پخش پذیری حسابان 2 به تقسیم و بخش‌پذیری چندجمله‌ای‌ها می‌پردازیم. برای یادآوری تقسیم چندجمله‌ای‌ها که در ریاضی نهم خواندید، می‌توانید قبل از شروع مطالعهٔ این درسنامه، درسنامهٔ تقسیم چند جمله ای ها نهم را مطالعه کنید. سعی می‌کنیم با استفاده از بیانی ساده و حل مثال‌های مختلف به درک بهتر شما از این مبحث کمک کنیم. با ما تا انتهای درسنامه همراه باشید.

قضیه تقسیم برای چند جمله ای ها

ابتدا قضیه تقسیم چند جمله ای ها را بیان می‌کنیم. سپس به حل مثال از آن می‌پردازیم.

قضیه تقسیم برای چند جمله ای ها: اگر \(\Large f(x)\) و \(\Large g(x)\) توابع چند جمله ای باشند و \(\Large g(x) \neq 0\) باشد، آنگاه چند جمله ای های یکتای \(\Large q(x)\) و \(\Large r(x)\) وجود دارند به صورتی که داشته باشیم:

\(\LARGE f(x)=g(x)q(x)+r(x)\)

که در عبارت بالا درجهٔ \(\Large r(x)\) از درجهٔ \(\Large g(x)\) کمتر است. به \(\Large q(x)\) خارج قسمت و به \(\Large r(x)\) باقی مانده می‌گوییم. 

در ریاضی نهم، تقسیم چندجمله ای ها بر یکدیگر را دیده‌ایم. برای یادآوری، در قالب یک مثال، روش تقسیم یک چند جمله ای بر چند جمله ای دیگر را مرور می‌کنیم. به مثال بعدی از درسنامهٔ تقسیم و بخش پذیری حسابان 2 توجه کنید.

مثال از تقسیم چند جمله ای ها بر هم

مثال 1: اگر \(\Large f(x)=4x^2+3+6x\) و \(\Large g(x)=2x+5\) باشد، حاصل تقسیم \(\Large f(x)\) بر \(\Large g(x)\) را بیابید.

حل: ابتدا باید جملات \(\Large f\) و \(\Large g\) را به صورت نزولی بر حسب درجه مرتب کنیم. یعنی مثلاً در \(\Large f\)، ابتدا جملهٔ درجه دوم که \(\Large 4x^2\) است، سپس جملهٔ درجه یکم که \(\Large 6x\) است و در آخر جملهٔ ثابت که \(\Large 3\) است را می‌آوریم:

\(\LARGE f(x)= 4x^2+6x+3\)

برای \(\Large g\) هم باید همین کار را انجام دهیم. البته \(\Large g\) از ابتدا مرتب شده به ما داده شده است. پس تقسیم به صورت زیر در می‌آید:

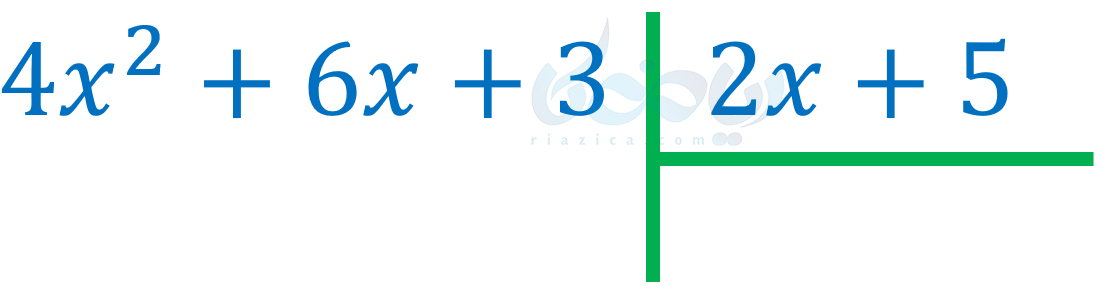
در این مرحله باید اولین جملهٔ \(\Large f\) را که \(\Large 4x^2\) است، بر اولین جملهٔ \(\Large g\) که \(\Large 2x\) است تقسیم کنیم. برای این کار کافی است ضرایب عددی را بر هم و عبارات جبری را بر هم تقسیم کرده و حاصل را در هم ضرب کنیم. برای اینکه بهتر متوجه شوید، برای تقسیم \(\Large 4x^2\) بر \(\Large 2x\) فرآیند زیر را طی می‌کنیم:

حاصل تقسیم \(\Large 4\) بر \(\Large 2\) برابر با \(\Large 2\) است. حاصل تقسیم \(\Large x^2\) بر \(\Large x\) برابر با \(\Large x\) است. بنابراین حاصل تقسیم \(\Large 4x^2\) بر \(\Large 2x\) برابر با \(\Large 2x\) می‌گردد. پس می‌نویسیم:

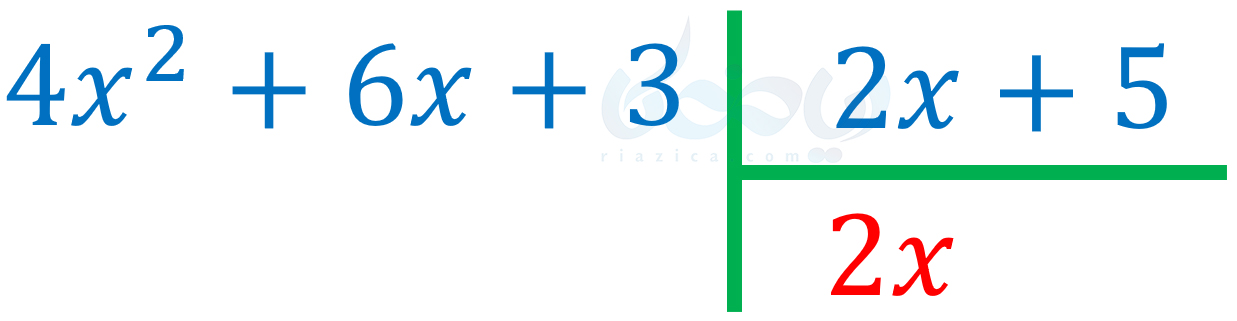
در این مرحله باید \(\Large 2x\) که در تصویر بالا به رنگ قرمز نشان داده شده است را در \(\Large 2x+5\) ضرب کرده و حاصل را از \(\Large 4x^2+6x+3\) کم کنیم. حاصل ضرب \(\Large 2x\) در \(\Large 2x+5\) به صورت زیر به دست می‌آید:

\(\LARGE 2x (2x+5)\)

\(\LARGE =4x^2+10x\)

پس می‌نویسیم:

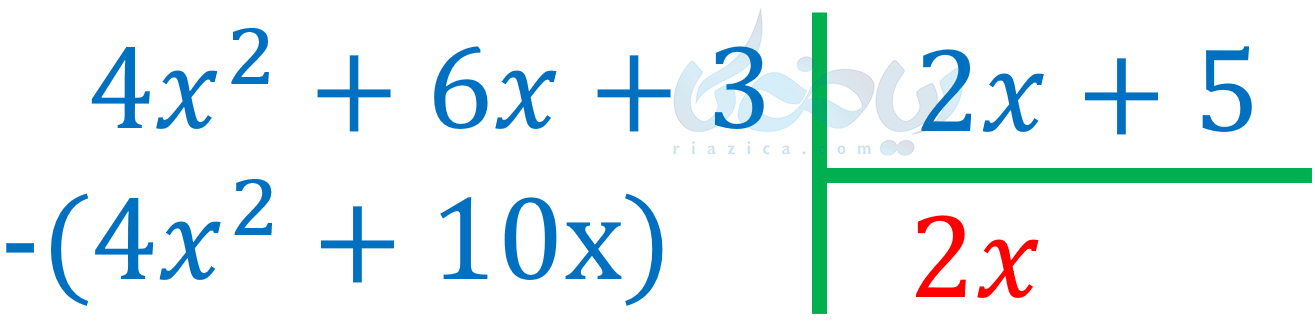
حالا باید تفاضل دو عبارت آبی رنگ را محاسبه کنیم. برای این کار کافی است جملات هم درجه را از یکدیگر کم کنیم؛ یعنی \(\Large 4x^2\) را از \(\Large 4x^2\) کم کرده و \(\Large 10x\) را از \(\Large 6x\) کم کنیم. در نهایت خواهیم داشت:

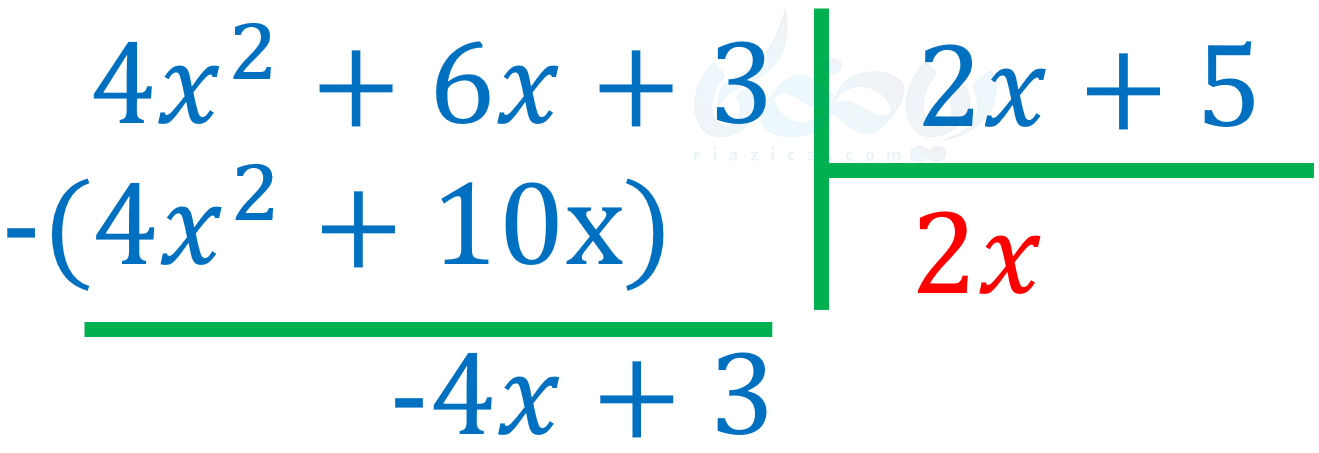
الآن باید \(\Large -4x+3\) را بر \(\Large 2x+5\) تقسیم کنیم. کافی است کارهای مراحل قبل را تکرار کنیم. یعنی جملهٔ اول \(\Large -4x+3\) را که \(\Large -4x\) است بر جملهٔ اول \(\Large 2x+5\) که \(\Large 2x\) است، تقسیم می‌کنیم. حاصل به صورت زیر در می‌آید:

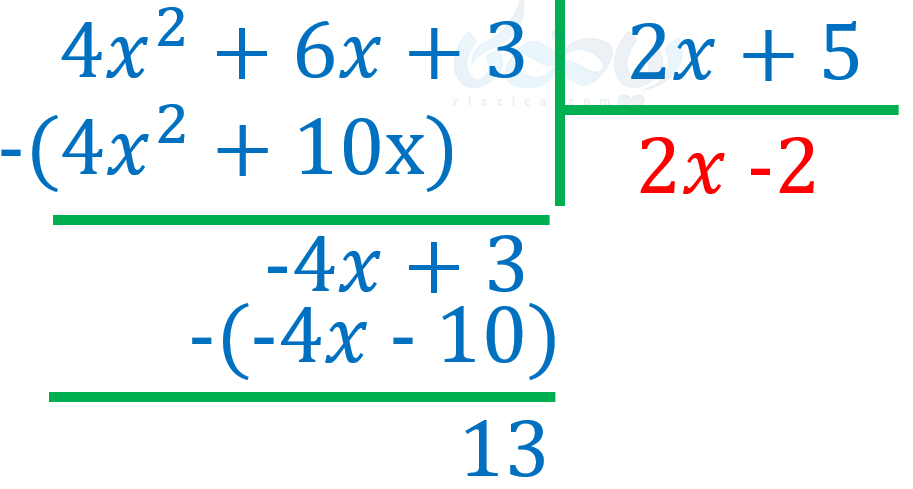
آیا باید تقسیم را ادامه دهیم؟ خیر. چون \(\Large 13\) چندجمله‌ای از درجهٔ صفر است و \(\Large 2x+5\) چندجمله‌ای از درجهٔ \(\Large 1\) است. بنابراین، درجهٔ باقی‌مانده کمتر از درجهٔ مقسوم‌ُعلیه است و تقسیم را متوقف می‌کنیم. به قسمت بعدی از درسنامهٔ تقسیم و بخش پذیری حسابان 2 توجه کنید.

باقی مانده تقسیم \(\Large f(x)\) بر \(\Large ax+b\)

باقی‌ماندهٔ تقسیم یک چند جمله‌ای بر \(\Large ax+b\) را می‌توان بدون انجام عملیات تقسیم به دست آورد. کافی است از قضیهٔ زیر استفاده کنیم. 

قضیه: باقی ماندهٔ تقسیم چند جمله ای \(\Large f(x)\) بر \(\Large ax+b\) برابر است با \(\Large f(-\frac{b}{a})\). به بیان ساده تر برای یافتن باقی ماندهٔ این تقسیم کافی است در \(\Large f(x)\) به جای \(\Large x\)، ریشهٔ \(\Large ax+b\) را قرار دهیم.

به طور مثال اگر بخواهیم باقی مانده تقسیم \(\Large f(x)=2x^2+3x+5\) را بر \(\Large 2x+6\) بیابیم، کافی است \(\Large f(-\frac{6}{2})\) یا همان \(\Large f(-3)\) را محاسبه کنیم:

\(\Large f(-3)= 2 \times (-3)^2+3 \times (-3) + 5\)

\(\LARGE = 18-9+ 5\)

\(\LARGE = 14\)

بنابراین، باقی مانده تقسیم \(\Large f(x)=2x^2+3x+5\) بر \(\Large 2x+6\) برابر است با \(\Large 14\). همان طور که دیدید، بدون انجام عملیات تقسیم، باقی مانده را به دست آوردیم.

چرا قضیه باقی مانده تقسیم برقرار است؟

اگرچه نمی‌خواهیم اثبات ریاضی برای قضیه باقی مانده تقسیم چند جمله ای ها ارائه کنیم، اما دوست داریم نسبت به این قضیه شهود مناسبی داشته باشید. اگر چند جمله ای \(\Large f(x)\) را بر \(\Large (ax+b)\) تقسیم کنیم، خواهیم داشت:

\(\LARGE f(x)=(ax+b)q(x)+r(x)\)

اگر در عبارت بالا به جای \(\Large x\) مقدار \(\Large -\frac{b}{a}\) که در واقع ریشهٔ \(\Large (ax+b)\) است را قرار دهیم، خواهیم داشت:

\(\LARGE f(-\frac{b}{a})=(a(-\frac{b}{a})+b)q(-\frac{b}{a})+r(-\frac{b}{a})\)

اگر عبارت بالا را ساده کنیم، داریم:

\(\Large f(-\frac{b}{a})=(-b+b)q(-\frac{b}{a})+r(-\frac{b}{a})\)

\(\LARGE \Rightarrow f(-\frac{b}{a})=0+r(-\frac{b}{a})\)

\(\LARGE \Rightarrow f(-\frac{b}{a})=r(-\frac{b}{a})\)

بنابراین مقدار \(\Large r(x)\) به ازای \(\Large x=-\frac{b}{a}\) برابر است با \(\Large f(-\frac{b}{a})\).

آنچه که گفتیم بسیار ناقص‌تر از یک اثبات ریاضی است. صرفاً قصد داشتیم یک شهود ابتدایی در شما ایجاد کنیم. در صورتی که علاقه‌مندید می‌توانید در مورد قضیهٔ کوچک بزو مطالعه کنید.

مثال از قضیهٔ باقی مانده تقسیم

مثال 2: باقی مانده تقسیم \(\Large f(x)=x^2+3x+7\) بر \(\Large 2x-1\) را بیابید.

حل: از آنجاییکه \(\Large 2x-1\) یک چند جمله ای درجهٔ اول است، می‌توانیم از قضیهٔ باقی مانده تقسیم چند جمله ای ها استفاده کنیم. بنابراین کافی است مقدار \(\Large f(x)\) را به ازای ریشهٔ \(\Large 2x-1\) که \(\Large \frac{1}{2}\) است به دست آوریم:

\(\LARGE r=f(\frac{1}{2})\)

\(\LARGE =(\frac{1}{2})^2+3 \times (\frac{1}{2})+7\)

\(\LARGE =\frac{1}{4}+\frac{3}{2}+7\)

\(\LARGE =\frac{35}{4}\)

مثال از درسنامهٔ تقسیم و بخش پذیری حسابان 2

مثال 3: باقی مانده تقسیم \(\Large f(x)=3x^5+2x^4+5x+6\) بر \(\Large x-1\) را بیابید.

حل: مانند مثال قبل از قضیهٔ باقی ماندهٔ تقسیم استفاده می‌کنیم. کافی است مقدار \(\Large f(x)\) را به ازای \(\Large x=1\) که همان ریشهٔ \(\Large x-1\) بیابیم:

\(\Large r=f(1)=3 \times 1^5+2 \times 1^4+5 \times 1+6\)

\(\LARGE =3+2+5+6=16\)

تجزیهٔ \(\Large x^n-a^n\)

تقسیم \(\Large x^n-a^n\) بر \(\Large x-a\) به صورت زیر در می‌آید:

همان طور که از تقسیم بالا می‌توان حدس زد، می‌توان ثابت کرد که \(\Large x^n-a^n\) به صورت زیر تجزیه می‌شود:

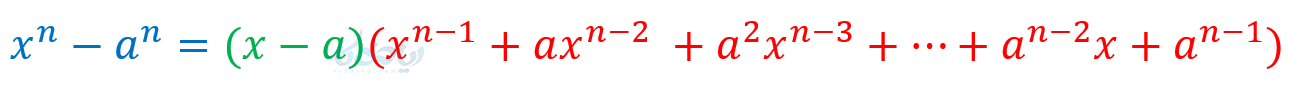
اگر دقت کنید در عبارت قرمز رنگ رابطهٔ بالا در هر جمله، مجموع توان \(\Large a\) و \(\Large x\) برابر است با \(\Large n-1\). جملهٔ اول فقط از \(\Large x\) تشکیل شده و جملهٔ آخر فقط از \(\Large a\) تشکیل شده است.

به مثال‌های بعدی از درسنامهٔ تقسیم و بخش پذیری حسابان 2 توجه کنید.

مثال از تجزیهٔ \(\Large x^n-a^n\)

مثال 4: خارج قسمت تقسیم \(\Large x^5-32\) بر \(\Large x-2\) را به دست آورید.

حل: در واقع باید خارج قسمت تقسیم \(\Large x^5-2^5\) بر \(\Large x-2\) را به دست بیاوریم. کافی است از تجزیه‌ای که آموختیم استفاده کنیم:

\( x^5-2^5=(x-2)(x^{4}+2x^{3}+2^2x^{2}+ 2^3x+2^4)\)

عبارت بالا را می‌توان به این صورت ساده کرد:

\( x^5-2^5=(x-2)(x^{4}+2x^{3}+4x^{2}+ 8x+16)\)

مثال از تقسیم و بخش پذیری حسابان 2

مثال 5: باقی مانده تقسیم \(\Large f(x)= x^4-81\) بر \(\Large x-3\) را بیابید.

حل: برای حل این مثال، هم می‌توانیم از قضیه باقی مانده تقسیم استفاده کنیم و هم می‌توانیم از تجزیهٔ \(\Large x^4-3^4\) استفاده کنیم. هر دو روش را می‌بینیم.

روش 1: طبق قضیهٔ باقی مانده تقسیم چند جمله ای ها، باقی ماندهٔ تقسیم \(\Large f(x)\) بر \(\Large x-3\) برابر است با \(\Large f(3)\). یعنی داریم:

\(\LARGE r=f(3)=3^4-81=0\)

روش 2: همین که می‌دانیم \(\Large f(x)\) به صورت حاصل ضربی از \(\Large x-3\) در یک عبارت دیگر تجزیه می‌شود، می‌توان نتیجه گرفت که \(\Large f(x)\) بر \(\Large x-3\) بخش‌پذیر بوده و باقی ماندهٔ تقسیم صفر است.  اما برای تمرین بیشتر، تجزیه یا همان رابطهٔ تقسیم را می نویسیم:

\(x^4-81=(x-3)(x^3+3x^2+9x+27)+0\)

همان طور که می‌بینید، خارج قسمت تقسیم برابر با \(\Large (x^3+3x^2+9x+27)\) و باقی ماندهٔ آن برابر با صفر است.

تغییر \(\Large a\) به \(\Large -a\) در تجزیهٔ \(\Large x^n-a^n\)

 در تجزیهٔ \(\Large x^n-a^n\) اگر \(\Large a\) را به \(\Large -a\) تغییر دهیم، بسته به اینکه \(\Large n\) زوج است یا فرد، دو رابطهٔ دیگر به دست می‌آید.

اگر \(\Large n\) فرد باشد، داریم:

 

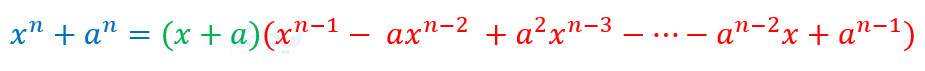
اگر \(\Large n\) زوج باشد، داریم:

 

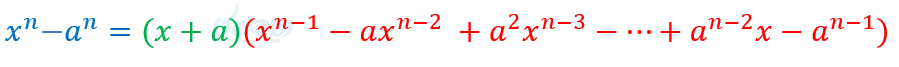
تنها تفاوت این روابط در علامت مثبت و منفی آن‌هاست که دلیل آن هم این است که وقتی \(\Large -a\) به توان زوج می‌رسد، علامت منفی از بین می‌رود.

مثال از درسنامهٔ تقسیم و بخش پذیری حسابان 2

مثال 6: چند جمله ای \(\Large x^5+32\) را تجزیه کنید.

حل: \(\Large n\) عددی فرد است، پس می‌توانیم از رابطه‌ای که دیدیم استفاده کنیم:

\(\LARGE x^5+32\)

\(\LARGE =x^5+2^5\)

\(=(x+2)(x^4-2x^3+4x^2-8x+16)\)

زنگ آخر درسنامهٔ تقسیم و بخش پذیری حسابان 2

در درسنامه‌ای که از حسابان 2 خواندیم، بخش پذیری و تقسیم چند جمله ای ها را بررسی کرده و مثال هایی از درس دوم کتاب حسابان 2 حل کردیم.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با درسنامهٔ تقسیم و بخش پذیری حسابان 2 دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.