معادلات مثلثاتی شامل تانژانت󠁴♓️➿ – آخرین بحث مثلثات!!

در درسنامهٔ معادلات مثلثاتی شامل تانژانت به بررسی دسته‌ای از معادلات مثلثاتی می‌پردازیم که در آن‌ها تابع تانژانت حضور دارد. سعی می‌کنیم با توضیح ساده و حل مثال‌های مرتبط با این مبحث از کتاب حسابان 2 به درک بهتر شما کمک کنیم. با ما تا پایان درسنامه همراه باشید.

معادلات مثلثاتی

به طور کلی به معادلاتی که شامل نسبت‌های مثلثاتی هستند، معادلات مثلثاتی می‌گویند. برای مثال، دو معادلهٔ زیر، معادلات مثلثاتی هستند:

\(\LARGE 2sin (x) + 3cos (x) =4\)

\(\LARGE tan (3x+2) =0\)

معادلهٔ اول شامل نسبت‌های مثلثاتی سینوس و کسینوس است. معادلهٔ دوم شامل نسبت مثلثاتی تانژانت است. از آنجاییکه قرار است در این درسنامه به بررسی معادلات شامل تانژانت بپردازیم، بهتر است نسبت مثلثاتی تانژانت و نحوهٔ به دست آوردن تانژانت یک زاویه در دایره مثلثاتی را به صورت کوتاه یادآوری کنیم. 

تانژانت یک زاویه و دایره مثلثاتی

همان طور که به یاد دارید، تانژانت یک زاویه در یک مثلث قائم الزاویه برابر است با نسبت ضلع مقابل به ضلع مجاور. برای درک بهتر به شکل زیر نگاه کنید:

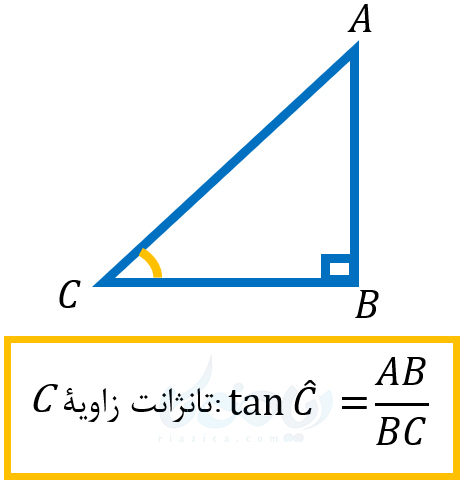
در دایرهٔ مثلثاتی (دایره به شعاع واحد) نیز، تانژانت یک زاویه بر روی محور تانژانت به صورت زیر نمایش داده می‌شود:

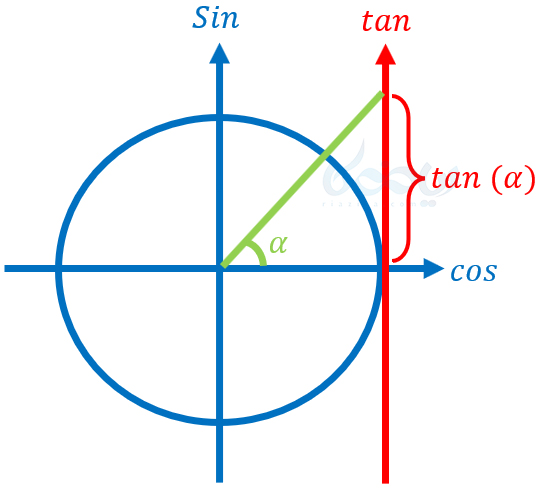
در صورتی که نیاز به مطالعه و حل تمرین بیشتر از نسبت‌های مثلثاتی دارید، می‌توانید درسنامهٔ آموزش نسبت‌های مثلثاتی دهم را مرور کنید. برای مطالعهٔ دقیق‌تر نسبت مثلثاتی تانژانت نیز می‌توانید به درسنامهٔ تانژانت مراجعه کنید. برای مرور مبحث دایرهٔ مثلثاتی نیز می‌توانید  درسنامهٔ دایرهٔ مثلثاتی را مطالعه کنید. در قسمت بعدی به بررسی معادلات شامل تانژانت می‌پردازیم.

تانژانت مجموع و تفاضل دو زاویه

با نسبت مثلثاتی تانژانت قبلاً آشنا بودید و مباحثی که تا این قسمت از درسنامه دیدید، صرفاً مرور مباحث گذشته بود. مباحثی که از این به بعد مطرح می‌شوند، جدید خواهند بود. می‌خواهیم \(\Large tan(\alpha+\beta)\) را بر حسب \(\Large tan(\alpha)\) و \(\Large tan(\beta)\) به دست آوریم. به عبارت دیگر به دنبال رابطه‌ای هستیم که با کمک آن بتوان با دانستن تانژانت دو زاویه، تانزانت مجموع آن‌ دو زاویه را نیز به دست آورد. طبیعتاً با توجه به مثال‌های نقضی که وجود دارد، می‌دانیم \(\Large tan(\alpha+\beta)\) با \(\Large tan(\alpha)+tan(\beta)\) متحد نیست. اما می‌توان رابطهٔ دیگری پیدا کرد. داریم:

\(\LARGE tan(\alpha+\beta)=\frac{sin(\alpha+\beta)}{cos(\alpha+\beta)}\)

از طرفی می‌دانیم که \(\Large sin(\alpha+\beta)\) و \(\Large cos(\alpha+\beta)\) را که سینوس و کسینوس مجموع دو زوایه هستند، می‌توان به صورت زیر نوشت:

\( sin(\alpha+\beta)=sin(\alpha)cos(\beta)+cos(\alpha)sin(\beta)\)

\( cos(\alpha+\beta)=cos(\alpha)cos(\beta)-sin(\alpha)sin(\beta)\)

بنابراین داریم:

\(\LARGE tan(\alpha+\beta)=\frac{sin(\alpha+\beta)}{cos(\alpha+\beta)}\)

\(\LARGE =\frac{sin(\alpha)cos(\beta)+cos(\alpha)sin(\beta)}{cos(\alpha)cos(\beta)-sin(\alpha)sin(\beta)}\)

اگر صورت و مخرج کسر بالا را بر \(\Large cos(\alpha)cos(\beta)\) تقسیم کنیم*، خواهیم داشت: 

\(\LARGE =\frac{\frac{sin(\alpha)cos(\beta)}{cos(\alpha)cos(\beta)}+\frac{cos(\alpha)sin(\beta)}{cos(\alpha)cos(\beta)}}{\frac{cos(\alpha)cos(\beta)}{cos(\alpha)cos(\beta)}-\frac{sin(\alpha)sin(\beta)}{cos(\alpha)cos(\beta)}}\)

اگر صورت و مخرج کسرهای بالا را ساده کنیم، به عبارت زیر می‌رسیم:

\(\LARGE =\frac{\frac{sin(\alpha)}{cos(\alpha)}+\frac{sin(\beta)}{cos(\beta)}}{1-\frac{sin(\alpha)sin(\beta)}{cos(\alpha)cos(\beta)}}\)

\(\LARGE =\frac{tan(\alpha)+tan(\beta)}{1-tan(\alpha)tan(\beta)}\)

بنابراین داریم:

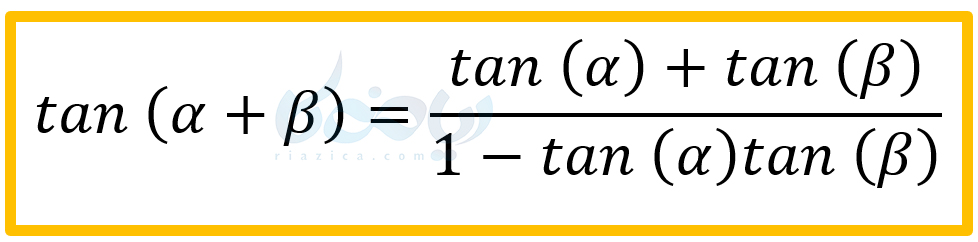
برای تانژانت تفاضل دو زاویه نیز کافی است در رابطهٔ بالا، \(\Large -\beta\) را به جای \(\Large \beta\) قرار می‌دهیم:

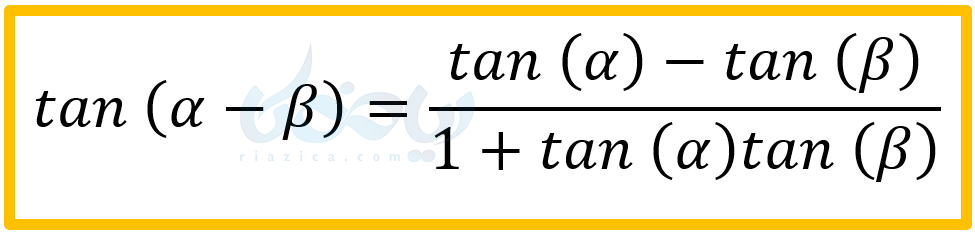
دقت مهم: جایی که با علامت * مشخص شده و صورت و مخرج را بر عبارت \(\Large cos(\alpha)cos(\beta)\) تقسیم کردیم، باید توجه می‌کردیم که \(\Large cos(\alpha)cos(\beta)\) در هیچ حالتی برابر با صفر نشود. خوشبختانه این امر همیشه اتفاق می‌افتد. زیرا این عبارت تنها در حالتی صفر می‌شود که \(\Large cos(\alpha)\) یا \(\Large cos(\beta)\) برابر با صفر شود. در این حالت هم تانژانت متناظر با آن زاویه نامتناهی شده و تعریف نشده است.

مثال از تانژانت مجموع و تفاضل دو زاویه

مثال 1: مقدار \(\Large tan(\frac{7\pi}{12})\) را محاسبه کنید.

حل: \(\Large \frac{7\pi}{12}\) را می‌توانیم به صورت \(\Large \frac{\pi}{4}+\frac{\pi}{3}\) بنویسیم. بنابراین داریم:

\(\LARGE tan(\frac{7\pi}{12})=tan(\frac{\pi}{4}+\frac{\pi}{3})\)

حال از رابطه‌ای که برای تانژانت مجموع دو زاویه به دست آوردیم، استفاده می‌کنیم:

\(\LARGE tan(\frac{\pi}{4}+\frac{\pi}{3})\)

\(\LARGE =\frac{tan(\frac{\pi}{4})+tan(\frac{\pi}{3})}{1-tan(\frac{\pi}{4})tan(\frac{\pi}{3})}\)

از آنجاییکه \(\Large tan(\frac{\pi}{4})=1\) و \(\Large tan(\frac{\pi}{3})=\sqrt{3}\) است، عبارت بالا برابر است با:

\(\LARGE \frac{1+\sqrt{3}}{1-\sqrt{3}}\)

بنابراین داریم:

\(\LARGE tan(\frac{7\pi}{12})=\frac{1+\sqrt{3}}{1-\sqrt{3}}\)

معادلات مثلثاتی شامل تانژانت

بالأخره به مبحث اصلی این درسنامه رسیدیم. می‌خواهیم روش حل معادلات مثلثاتی شامل تانژانت را بررسی کنیم. طبیعتاً معادلات مثلثاتی بسیار متنوعی وجود دارند که شامل تانژانت نیز هستند. در سال دوازدهم تنها به حل برخی از این معادلات می‌پردازیم. برای اینکه مطالب نظم مناسبی داشته باشند، معادلات شامل تانژانتی که باید فرا بگیریم را به دو دسته تقسیم می‌کنیم. معادلاتی که خارج از این دو دسته قرار دارند را نیز باید با ساده‌سازی به شکل یکی از این دوع معادله درآوریم.

نوع اول: معادلات به شکل \(\Large tan(x)=tan(\alpha)\)

در بسیاری از حالات، با معادلاتی سروکار داریم که دو طرف معادله به صورت تانژانت یک زاویه است. معادلهٔ \(\Large tan(x)=tan(\alpha)\) را در نظر می‌گیریم. بدیهی است که یکی از جواب‌های این معادله، \(\Large x=\alpha\) است. اما جواب دیگری هم دارد؟ بله. تانژانت، یک تابع متناوب با دورهٔ تناوب \(\Large \pi\) است؛ یعنی مثلاً اگر \(\Large tan(x)=1\) شده باشد، \(\Large tan(x+\pi)\) نیز برابر با \(\Large 1\) می‌شود. \(\Large tan(x-\pi)\) نیز برابر با \(\Large 1\) می‌شود. به بیان دیگر هر مضرب صحیح از \(\Large \pi\) که به \(\Large x\) اضافه کنیم، جواب تغییری نخواهد کرد. (در صورتی که مبحث توابع متناوب را فراموش کرده‌اید، درسنامهٔ دوره تناوب را مطالعه کنید). برای درک بهتر می‌توانید به نمودار تابع تانژانت نیز که در شکل زیر رسم شده نگاه کنید:

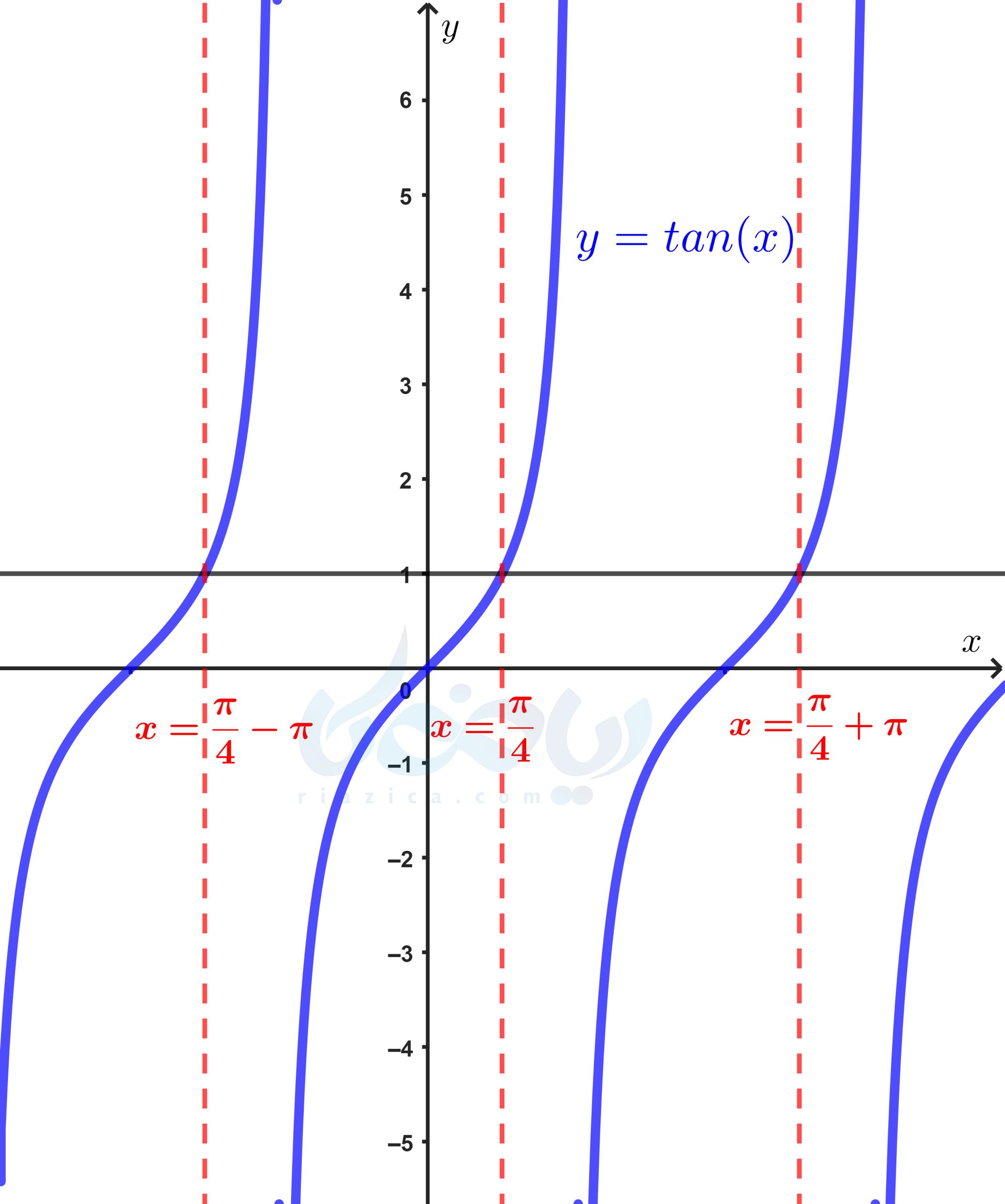
همان طور که در شکل بالا می‌بینید، تانژانت زاویهٔ \(\Large \frac{\pi}{4}\) برابر با \(\Large 1\) است. اگر به مقدار \(\Large \pi\) در جهت مثبت محور \(\Large x\)ها یا در جهت منفی محور \(\Large x\)ها حرکت کنیم نیز، \(\Large tan(x)\)  برابر با \(\Large 1\) خواهد شد. به طو کلی هر مضرب صحیحی از \(\Large \pi\) نیز که به \(\Large x\) اضافه کنیم، همین اتفاق می‌افتد. از دایرهٔ مثلثاتی هم می‌توانستیم کمک بگیریم. به شکل زیر نگاه کنید:

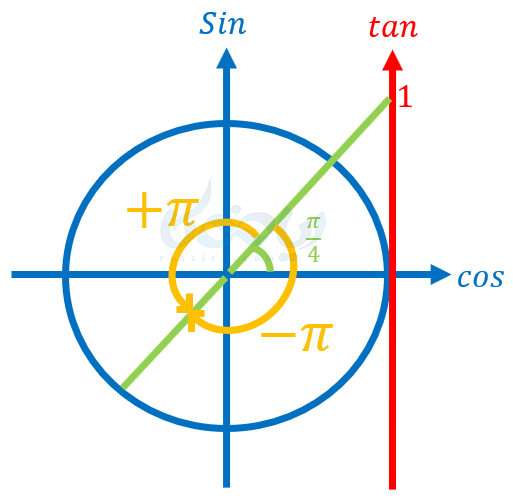
همان طور که در شکل بالا می‌بینید، تانژانت زاویهٔ \(\Large \frac{\pi}{4}\) برابر با \(\Large 1\) است. اگر به مقدار \(\Large \pi\) در جهت مثلثاتی یا خلاف جهت مثلثاتی حرکت کنیم نیز، \(\Large tan(x)\)  برابر با \(\Large 1\) خواهد شد. به طو کلی هر مضرب صحیحی از \(\Large \pi\) نیز که به \(\Large x\) اضافه کنیم، همین اتفاق می‌افتد. پس به طور کلی، پاسخ معادلهٔ \(\Large tan(x)=tan(\alpha)\) برابر با \(\Large x=k\pi+\alpha\) خواهد بود که در آن \(\Large k\) یک عدد صحیح است.

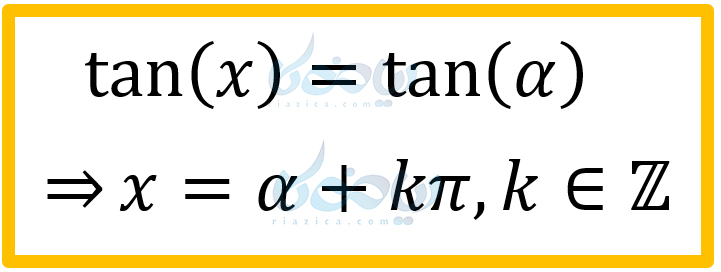
در عبارت بالا، منظور از \(\LARGE k \in \mathbb{Z}\) این است که \(\LARGE k\) عضو مجموعهٔ اعداد صحیح است.

نوع دوم: معادلات به شکل \(\Large tan(x)=a\)

اگر بتوانیم معادلهٔ \(\Large tan(x)=a\) را به صورت معادلات نوع اول که در قسمت قبل دیدیم در بیاوریم، می‌توانیم با استفاده از رابطه‌ای که در قسمت قبل به دست آوردیم، آن‌ها را حل کنیم. اما آیا این کار ممکن است؟ جواب مثبت است. \(\Large a\) هر مقداری که باشد، می‌توان یک زاویه مانند \(\Large \alpha\) پیدا کرد که \(\Large tan(\alpha)=a\) شود. مثلاً فرض کنید معادلهٔ \(\Large tan(x)=\sqrt{3}\) به ما داده شده است. از آنجاییکه \(\Large tan(\frac{\pi}{3})=\sqrt{3}\) است، می توانیم معادلهٔ داده شده را به صورت زیر بازنویسی کنیم:

\(\LARGE tan(x)=tan(\frac{\pi}{3})\)

الآن معادله به شکل معادلات نوع اول درآمده است.. همان طور که در معادلات نوع اول دیدیم، جواب معادلهٔ بالا به صورت زیر است:

\(\LARGE x=\frac{\pi}{3}+k\pi\)

که \(\Large k\) در عبارت بالا یک عدد صحیح است.

مثال از معادلات مثلثاتی شامل تانژانت

مثال 2: معادلهٔ \(\Large tan(3x)=tan(2x)\) را حل کنید.

حل: معادلهٔ داده شده به شکل معادلات نوع اول است. بنابراین داریم:

\(\LARGE 3x=2x+k\pi\)

\(\LARGE \Rightarrow x=k\pi, k \in \mathbb{Z}\)

مثال از معادلات مثلثاتی شامل تانژانت

مثال 3: معادلهٔ \(\Large tan(3x+6)=0\) را حل کنید.

حل: معادلهٔ داده شده از معادلات نوع دوم است. بنابراین باید یک زاویه پیدا کنیم که تانژانت آن برابر با صفر باشد. \(\Large tan(0)=0\) است. پس داریم:

\(\LARGE tan(3x+6)=tan(0)\)

الآن یک معادلهٔ نوع اول داریم. پس:

\(\LARGE 3x+6=0+k\pi\)

\(\LARGE \Rightarrow  3x=k\pi-6\)

\(\LARGE \Rightarrow  x=\frac{k\pi}{3}-2, k \in \mathbb{Z}\)

مثال از معادلات مثلثاتی شامل تانژانت

مثال 4: معادلهٔ \(\Large \sqrt{3}tan(x)+\sqrt{3}tan(2x)=1-tan(x)\) را که در آن \(\Large tan(x)\neq 1\) است، حل کنید.

حل: معادلهٔ داده شده به نظر به هیچ یک از دو نوعی که دیده بودیم شبیه‌ نیست. اما اگر معادله را ساده کنیم، می‌توانیم معادله را به شکل معادلات نوع اول درآوریم. از آنجاییکه در صورت مسئله گفته شده \(\Large tan(x)\neq 1\) است، \(\Large 1-tan(x) \neq 0\) می‌شود و می‌توانیم دو طرف معادله را بر \(\Large 1-tan(x) \) تقسیم کنیم (با تقسیم دو طرف معادله بر یک عبارت غیر صفر، معادله تغییری نمی‌کند):

\(\LARGE \frac{\sqrt{3}tan(x)+\sqrt{3}tan(2x)}{1-tan(x)}=\frac{1-tan(x)}{1-tan(x)}\)

\(\LARGE \Rightarrow \frac{\sqrt{3}(tan(x)+tan(2x))}{1-tan(x)}=1\)

\(\LARGE \Rightarrow \frac{tan(x)+tan(2x)}{1-tan(x)}=\frac{1}{\sqrt{3}}\)

حال اگر دقت کنید، طرف چپ عبارت بالا طبق رابطه‌ای که برای تانژانت مجموع دو زاویه داشتیم، برابر است با \(\Large tan(x+2x)\). بنابراین داریم:

\(\LARGE  tan(x+2x)=\frac{1}{\sqrt{3}}\)

\(\LARGE  \Rightarrow tan(3x)=\frac{1}{\sqrt{3}}\)

حالا یک معادلهٔ نوع دوم در اختیار داریم. می‌دانیم \(\Large tan(\frac{\pi}{6})=\frac{1}{\sqrt{3}}\). بنابراین برای حل معادلهٔ بالا به صورت زیر عمل می‌کنیم:

\(\LARGE  tan(3x)=tan(\frac{\pi}{6})\)

\(\LARGE  \Rightarrow 3x=\frac{\pi}{6}+k\pi\)

\(\LARGE  \Rightarrow x=\frac{\pi}{18}+\frac{k\pi}{3}, k \in \mathbb{Z}\)

زنگ آخر درسنامهٔ معادلات مثلثاتی شامل تانژانت

در درسنامه‌ای که از حسابان 2 خواندیم، معادلات مثلثاتی که شامل تانژانت هستند را بررسی کرده و مثال هایی از درس دوم کتاب حسابان 2 حل کردیم.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با درسنامهٔ معادلات مثلثاتی شامل تانژانت دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.