پاسخنامه تشریحی سوالات ریاضی تیزهوشان نهم ۹۹-۱۴۰۰ ??!

در این صفحه پاسخنامه تشریحی سوالات ریاضی تیزهوشان نهم ۹۹-۱۴۰۰ را دریافت می‌کنید.

سوالات ریاضی تیزهوشان نهم ۹۹-۱۴۰۰

سوال ۹۱: اگر \(\Large |a-b|=a-b \) و \(\Large a-c=b  \) آنگاه کدام یک از گزینه های زیر، همواره درست است؟ \(\Large abc \ne 0)  \))

1. \(\Large \frac{a}{c^2}>0 \)
2. \(\Large \frac{b}{c^2}>0 \)
3. \(\Large \frac{b}{a^2}>0 \)
4. \(\Large \frac{c}{b^2}>0 \)

حل ۹۱: گزینه ۴

سوال ۹۲: اگر حاصل عبارت \(\Large (\frac{1}{4})^{x-1}\times (-5^{y+3})^{-2}\times (-3^{-2})^\frac{3-x-z}{2}  \) به صورت \(\Large 10^k \) باشد \(\Large k \in , k \ne 0)  \)) ؛ حاصل عبارت \(\Large  x^2+xz-xy-yz  \) برابر است با:

1. \(\Large -6 \)
2. \(\Large 6 \)
3. \(\Large -12 \)
4. \(\Large 12 \)

حل ۹۲: گزینه ۴

سوال ۹۳: اگر \(\LARGE  3[\begin{matrix} 2a  \\-3\end{matrix}] +[\begin{matrix} 4  \\2-3a\end{matrix}] -2 x =[\begin{matrix} 3  \\1\end{matrix}] \)  و بردار \(\Large x  \) روی نیمساز ناحیه سوم قرار داشته باشد؛ مقدار \(\Large a  \) برابر است با:

1. ۱
2. ۱-
3. ۲
4. ۲-

حل ۹۳: گزینه ۲

سوال ۹۴: در شکل مقابل، نقطه \(\Large B  \) روی پاره خط \(\Large AC  \) و نقطه \(\Large E  \) روی پاره خط \(\Large FD  \)  قرار دارد. اگر \(\Large F\hat A B + D \hat E B =200^0  \) ، اندازه \(\Large D\hat C B   \) چند درجه است؟

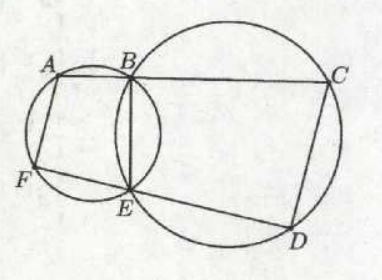
1. \(\Large 40 \)
2. \(\Large 50 \)
3. \(\Large 80 \)
4. \(\Large 100 \)

حل ۹۴: گزینه ۳

سوال ۹۵: مجموعه \(\Large S=\{x|2x^2 \in  , -2 \leq x \leq 2 \} \) را در نظر بگیرید. به صورت تصادفی یکی از اعضای \(\Large S  \) را انتخاب می کنیم؛ پیشامد \(\Large A  \) را به این صورت تعریف می کنیم که عدد انتخاب شده، گنگ باشد. در این صورت چندتا از گزاره های زیر درست خواهد بود؟

\(\Large P(A)=0 , n(S)=5 , n(A)>n(S)-n(A)  \)

1. صفر
2. یک
3. دو
4. سه

حل ۹۵: حذف

سوال ۹۶: دو مثلث \(\Large ABC  \) که \(\Large AB=AC  \)  ، نقاط  \(\Large X , Y  \)  روی ضلع \(\Large AC  \) طوری قرار گرفته که \(\Large X  \) بین \(\Large A  \) و \(\Large Y \) قرار دارد و همچنین \(\Large BY=AX=BX  \) ، اگر زاویه \(\Large YBC  \) برابر  ۱۰ درجه باشد، زاویه \(\Large BAC  \) چند درجه است؟

1. \(\Large \frac{95}{3} \)
2. \(\Large 38 \)
3. \(\Large 40 \)
4. \(\Large 41 \)

حل ۹۶: گزینه ۳

سوال ۹۷: اگر \(\Large A , B  \) دو مجموعه باشند به طوریکه \(\Large (A-B) \subseteq  , (B-A) \subseteq        \)  \(\Large A\cap B \subseteq  \) و \(\Large b \in B , a \in A \) ؛ آنگاه کدام گزینه همواره درست خواهد بود؟

1. \(\Large (\sqrt{3} b- a )\in   \)
2. \(\Large (2b -\sqrt{3} a )\in  \)
3. \(\Large (3b+4a )\in  \)
4. \(\Large (-2b+4a )\in  \)

حل ۹۷: حذف

سوال ۹۸: مریم اعداد ۱ تا ۲۵ را در دو دسته جدا از هم نوشته است. (هر عدد فقط یکبار نوشته شده است) او سپس چندتا از این اعداد را حذف کرد به طوریکه حاصل ضرب عددهای هر دسته با دسته دیگر برابر شود. مریم حداقل چند عدد را حذف کرده است؟

1. \(\Large 4  \)
2. \(\Large 5  \)
3. \(\Large 6 \)
4. \(\Large 7 \)

حل ۹۸: گزینه ۲

سوال ۹۹: یک اسفنج مکعب شکل به ضلع \(\Large a \) را با یک چاقو به این صورت می بریم که هم زمان از چهارنقطه \(\Large A,B,C,D \) میگذرد. \(\Large A , B  \) راس های مکعب و  \(\Large D,C  \) وسط های یال های مکعب هستند. مساحت چهارضلعی \(\Large ABCD  \) کدام است ؟

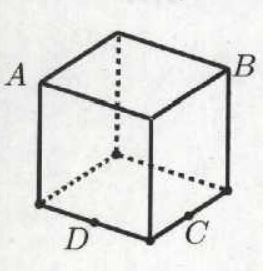
1. \(\Large \frac{9}{2}a^2 \)
2. \(\Large \frac{3\sqrt{2}}{4}a^2 \)
3. \(\Large \frac{9}{8}a^2 \)
4. \(\Large \frac{9}{4}a^2 \)

حل ۹۹: گزینه ۳

سوال ۱۰۰: اگر \(\Large A=\{x|x \in Z , 0 <x<100\} \) و \(\Large B \) زیر مجموعه ای از \(\Large A \) باشد به طوریکه هر دو عضو دلخواه که از \(\Large B \) در نظر بگیریم، یکی شمارنده دیگری باشد، در اینصورت مجموعه \(\Large B \) حداکثر چند عضو دارد؟

1. \(\Large 6 \)
2. \(\Large 7 \)
3. \(\Large 8 \)
4. \(\Large 9 \)

حل ۱۰۰: گزینه ۲

زنگ آخر پاسخنامه تشریحی سوالات ریاضی تیزهوشان نهم ۹۹-۱۴۰۰

دوستان ریاضیکا، حتما ویدیو و پاسخنامه تشریحی سوالات ریاضی تیزهوشان نهم ۹۹-۱۴۰۰ را تهیه کنید. هر سوالی داشتید در قسمت دیگاه می‌توانید از کارشناسان ریاضیکا بپرسید.