آموزش ریاضی پایه هفتم
تبدیلات هندسی ریاضی هفتم 📆🧨 – همه حرکتها!
در درسنامۀ تبدیلات هندسی ریاضی هفتم ابتدا با یک تبدیل هندسی جدید به نام انتقال آشنا خواهیم شد. سپس، دو تبدیل هندسی دیگر، یعنی تقارن و دوران را که در سالهای گذشته با آنها آشنایی شدید مرور میکنیم. برای هر یک از این تبدیلات نیز مثالهای مختلفی حل خواهیم کرد. بازم به ذکر است که هدف این مبحث از کتاب ریاضی هفتم، تنها یک آشنایی اجمالی با تبدیلات هندسی است. بنابراین در آنها از تعریفهای دقیق ریاضی استفاده نشده است. در آینده این تبدیلات را با تعریفهای دقیقتر خواهید آموخت. تا انتهای درسنامۀ تبدیلات هندسی ریاضی هفتم با ما همراه باشید.
انتقال
به زبان خیلی ساده، وقتی میگوییم یک شکل انتقال یافته، یعنی بدون تغییر جهت و اندازه حرکت کرده است. مثلاً در تصویر زیر، شکل \(\Large B\) از انتقال شکل \(\Large A\) به دست آمده است.
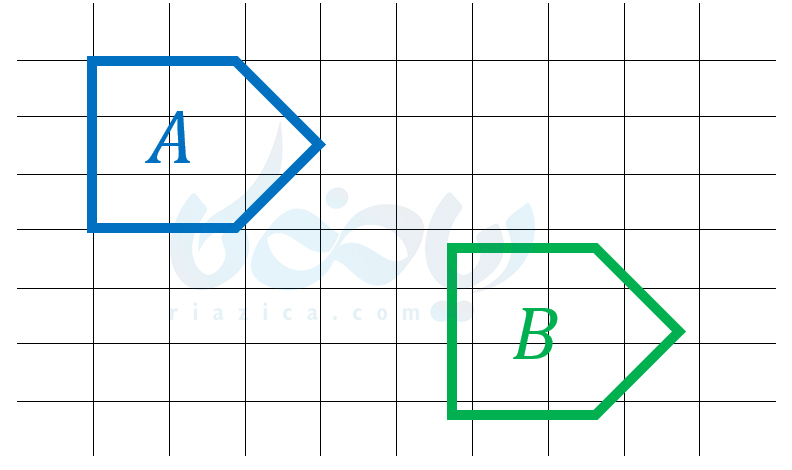
به مثال زیر از درسنامۀ تبدیلات هندسی ریاضی هفتم دقت کنید.
مثال از انتقال
مثال 1: کدام یک از شکلهای زیر، انتقال یافتۀ شکل \(\Large A\) است؟
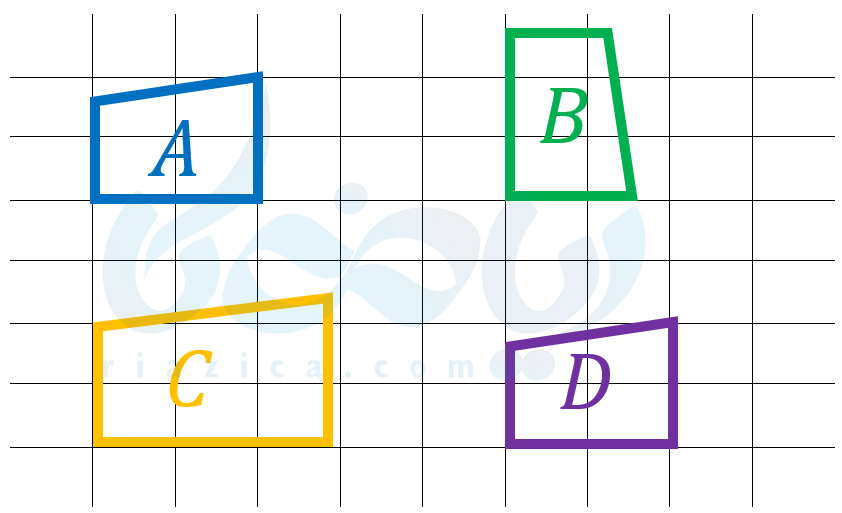
حل: با انتقال یک شکل، ابعاد و جهت آن تغییری نمیکنند. جهت شکل \(\Large A\) و \(\Large B\) یکی نیست. ابعاد شکل \(\Large A\) با شکل \(\Large C\) متفاوت است. بنابراین نه شکل \(\Large B\) و نه شکل \(\Large C\) انتقال یافتۀ شکل \(\Large A\) نیستند. اما شکل \(\Large D\) هم جهت و هم ابعاد شکل \(\Large A\) را حفظ کرده است. بنابراین پاسخ مسئله، شکل \(\Large D\) است. به مثال بعدی از درسنامۀ تبدیلات هندسی ریاضی هفتم دقت کنید.
مثال از انطباق شکل
مثال 2: با چند انتقال میتوانیم شکل \(\Large A\) را بر شکل \(\Large B\) منطبق کنیم؟
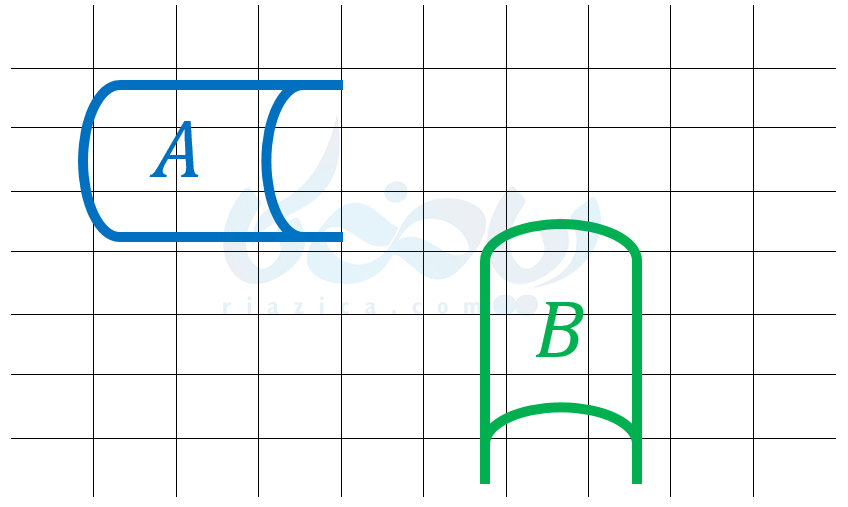
حل: با هیچ تعداد انتقالی نمیتوانیم شکل \(\Large A\) را بر شکل \(\Large B\) منطبق کنیم. زیرا در هر انتقال، جهت شکل حفظ میشود. بنابراین بعد از هر انتقال باید جهت شکل بدون تغییر بماند. اما جهت شکل \(\Large A\) با جهت شکل \(\Large B\) یکسان نیست. بنابراین با هیچ تعداد انتقالی نمیتوانیم شکل \(\Large A\) را بر شکل \(\Large B\) منطبق کنیم. به قسمت بعدی از درسنامۀ تبدیلات هندسی ریاضی هفتم دقت کنید.
تقارن
با تقارن در سالهای گذشته آشنا شدهاید. همانطور که میدانید دو نوع تقارن مرکزی و محوری داریم. تقارن مرکزی یک نوع دوران نیز هست. بنابراین در این قسمت به تقارن محوری پرداخته و در قسمت بعد، از تقارن مرکزی صحبت میکنیم. برای پیدا کردن قرینۀ محوری یک شکل، از هر نقطه از شکل به محور تقارن عمود رسم کرده و آن را به اندازۀ فاصلۀ نقطه از محور تقارن ادامه میدهیم تا به نقطۀ قرینه برسیم. مثلاً در تصویر زیر، شکل \(\Large B\) از قرینۀ محوری شکل \(\Large A\) نسبت به خط \(\Large d\) به دست آمده است:
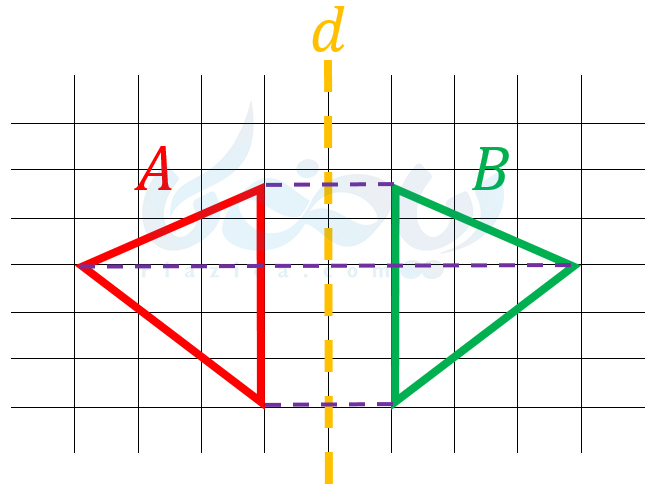
همان طور که میبینید، در قرینۀ محوری، جهت شکل تغییر کرده اما ابعاد آن حفظ شده است. به مثال بعدی از درسنامۀ تبدیلات هندسی ریاضی هفتم دقت کنید.
مثال از تقارن در تبدیلات هندسی ریاضی هفتم
مثال 3: در تصویر زیر، شکل \(\Large B\) از قرینۀ محوری شکل \(\Large A\) به دست آمده است. محور تقارن را مشخص کنید.
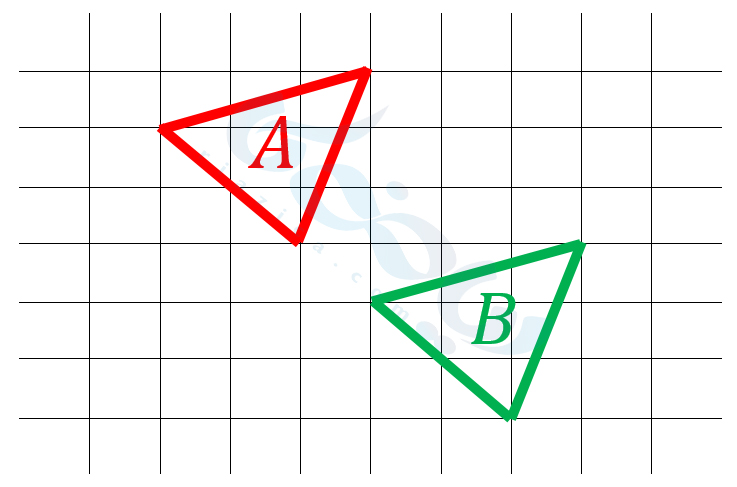
حل: مانند شکل زیر، دو نقطۀ \(\Large M\) و \(\Large N\) را به هم وصل کرده و عمود منصف پارهخط \(\Large MN\) را رسم میکنیم تا خط \(\Large d\) حاصل شود.
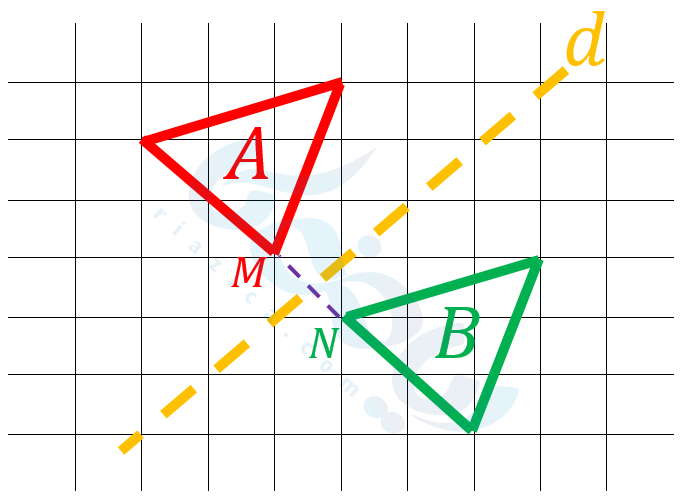
همان طور که میبینید، خط \(\Large d\)، محور تقارن دو شکل \(\Large A\) و \(\Large B\) است (برای اثبات دقیق تر، باید عمود منصف خطوط واصل نقاط دیگر را نیز رسم میکردیم. زیرا لزوماً نمیتوان گفت قرینۀ نقطۀ \(\Large M\)، نقطۀ \(\Large N\) است. اما اگر حالات دیگر را نیز بررسی کنید، خواهید دید که خط \(\Large d\) پاسخ مسئله است). به قسمت بعدی از درسنامۀ تبدیلات هندسی ریاضی هفتم دقت کنید.
دوران
به بیان خیلی ساده و غیر دقیق، زمانی که نقاط یک شکل را حول یک نقطه می چرخانیم، آن شکل را حول آن نقطه (که به آن مرکز دوران می گوییم) دوران دادهایم. زاویۀ چرخش و جهت آن اهمیت دارد. به طور مثال در تصویر زیر، شکل \(\Large A\) را \(\Large 90\) درجه حول نقطۀ \(\Large O\) خلاف جهت عقربههای ساعت دوران دادهایم تا شکل \(\Large B\) حاصل شود:
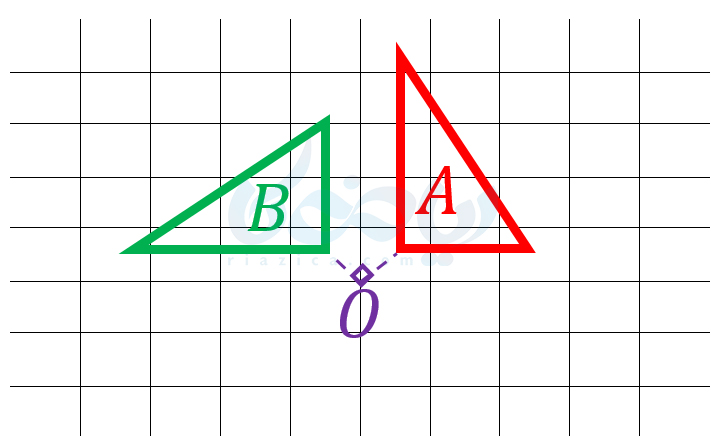
اگر همین دوران را در جهت عقربههای ساعت انجام میدادیم، شکل زیر حاصل میشد:
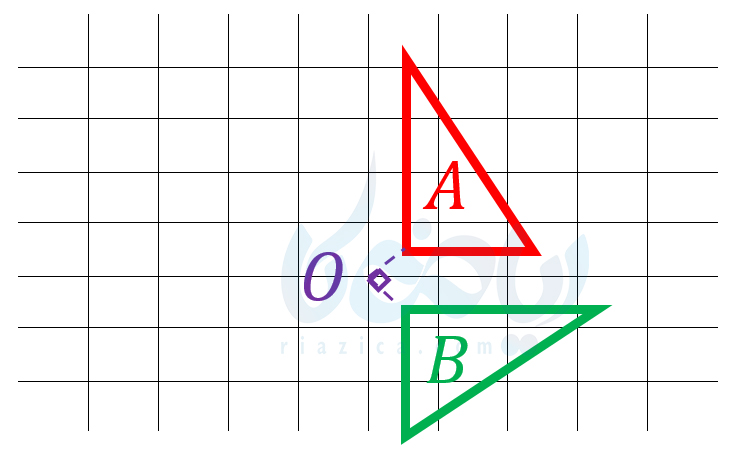
به قسمت بعدی از درسنامۀ تبدیلات هندسی ریاضی هفتم دقت کنید.
دوران 180 درجه یا تقارن مرکزی
همان طور که در قسمت قبل گفتیم، تقارن مرکزی حالت خاصی از دوران است. در تقارن مرکزی، هر نقطه از شکل را به مرکز تقارن وصل کرده و به اندازۀ فاصلۀ نقطه از مرکز تقارن ادامه میدهیم تا به نقطۀ قرینه برسیم. در دوران \(\Large 180\) درجه نیز دقیقاً همین اتفاق میافتد. تفاوتی هم نمیکند که جهت دوران \(\Large 180\) درجه در جهت عقربههای ساعت است یا خلاف آن. مثلاً در تصویر زیر، شکل \(\Large B\) از دوران \(\Large 180\) درجۀ شکل \(\Large A\) نسبت به نقطۀ \(\Large O\) به دست آمده است:
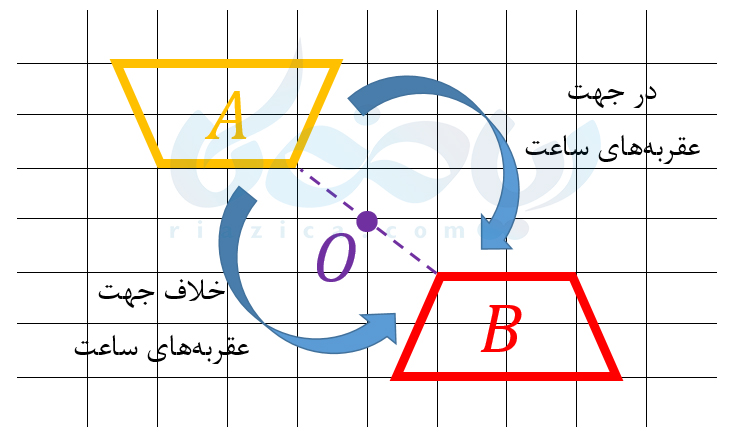
همانطور که میبینید تفاوتی نمیکند که شکل \(\Large A\) را در جهت عقربه های ساعت یا خلاف آن حول نقطۀ \(\Large O\) دوران \(\Large 180\) درجه دهیم. در هر صورت شکل \(\Large B\) حاصل می شود. به مثال بعدی از درسنامۀ تبدیلات هندسی ریاضی هفتم دقت کنید.
مثال از دوران در تبدیلات هندسی ریاضی هفتم
مثال 5: در تصویر زیر، شکل \(\Large A\) را \(\Large 180\) درجه حول نقطۀ \(\Large O\) دوران داده و سپس قرینۀ آن را نسبت به خط \(\Large d\) به دست آورید.
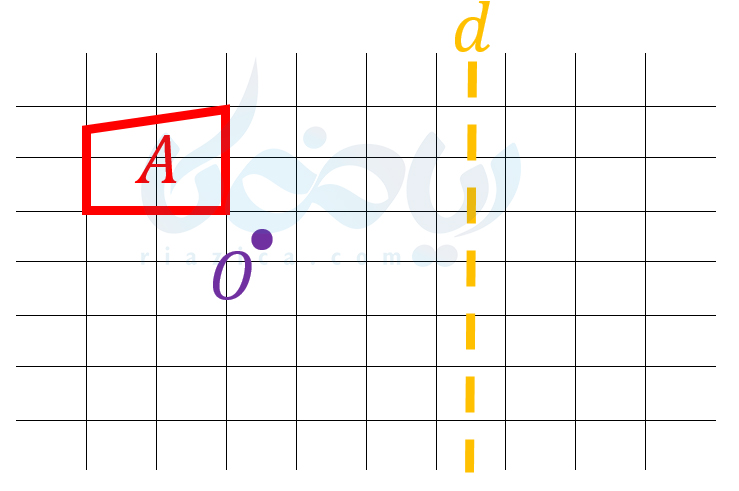
حل: همانطور که گفتیم، در دوران \(\Large 180\) درجه نیازی به تعیین جهت دوران نیست. همچنین، همان طور که در قسمت قبل گفتیم، دوران 180 درجه حول یک نقطه، همان قرینۀ مرکزی نسبت به آن نقطه است. بنابراین ابتدا قرینۀ مرکزی شکل \(\Large A\) را نسبت به نقطۀ \(\Large O\) به دست میآوریم تا شکل \(\Large B\) حاصل شود:
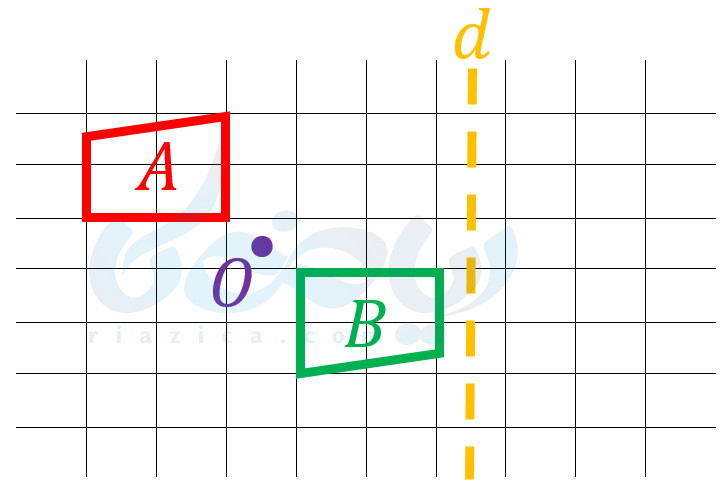
حال قرینۀ محوری شکل \(\Large B\) را نسبت به خط \(\Large d\) به دست میآوریم:
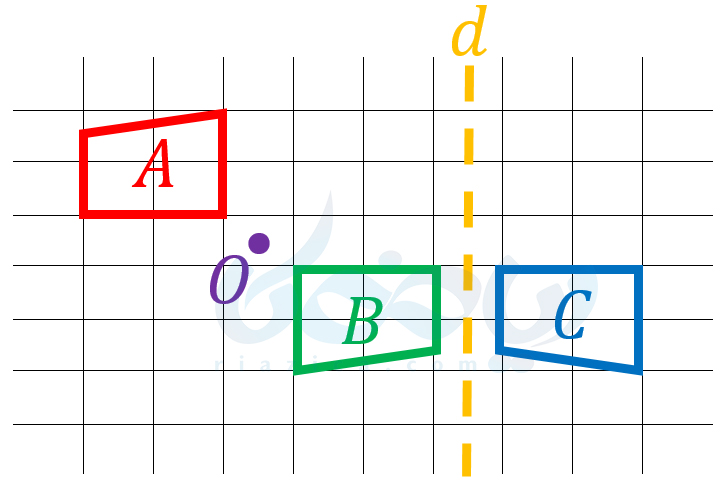
شکل \(\Large C\) جواب مسئله است.
برای خوندن مطالب بیشتر در مورد انتفال به پست بردار انتقال ریاضی هفتم مراجعه کنید و برای خوندن ادامه مطلب به پست شکلهای هم نهشت مراجعه کنید.
زنگ آخر کلاس تبدیلات هندسی ریاضی هفتم
در این درسنامه از ریاضی هفتم با تبدیل هندسی انتقال آشنا شدیم. دیدیم که به زبان ساده، انتقال در واقع همان حرکت شکل بدون تغییر جهت و ابعاد آن است. همچنین، تبدیلات تقارن و دوران را که در سالهای گذشته فرا گرفته بودیم، مرور کرده و مثالهای مختلفی از این تبدیلات هندسی حل کردیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث تبدیلات هندسی ریاضی هفتم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





خیلی عالی بود ممنون
سلام و عرض ادب
ممنون از توجهاتتون
موفق باشید
اشتراکها: یاشار
با سلام وعرض ادب
خدا رو شکر که براتون مفید بوده
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
مرررررررررسیعالیییییییییبیییبودایول
با سلام واحترام
ممنون از نظر توجه شما
مرررررررررسیعالیییییییییبیییبودایول
با سلام وعرض ادب
خوشحالیم که مفید بوده
خوب
چگونه شکل c جواب اومد ؟
با سلام وعرض ادب
اول ۱۸۰ درجه دوران دادیم بعد قرینه محوری رو نسبت به خطدی بدست آوردیم
خیلی خوب بود
ممنون دوست عزیز
عااااالی بود?
با سلام ووقت به خیر
ممنون از نظر لطف سما
سلام میشه نام هندسی رو بگین
با سلام وادب
منظور شما رو متوجه نشدم
خیلی خوب بود. برای ترم دوم این مبحث رو کامل از سایت شما یاد گرفتم.
با سلام وعرض احترام
خدا رو شکر که ما هدف خود که آموزش ریاضی به صورت آسان است رسیده ایم
لطفا در مورد بازتاب هم توضیح بدین
سلام بسیاربسیارعالی بودممنون ازتوضیحات بابیان ساده موفق وسلامت باشید
با سلام وادب
خدا رو شکر که مفید بوده
سلام…ممنون میشم کمکم کنید.اگر یک شکلی دادند و گفتند چه تبدیلی انجام شده، و اگر این تبدیل تقارن محوری و انتقال نبود، چگونه تشخیص بدیم که دروان هست یا تقارن مرکزی؟ من در تشخیص دوران و تقارن مرکزی ضعف دارم.و در امتحان چگونه بدون طلق میتوانیم شکلی رو دوران دهیم؟
خیلی فوق العاده بود
با سلام و ادب
ممنون از نظر لطف شما
عالی
با سلام وادب
خوشحالیم که مفید واقع شده
ممنون، واقعا عالی بود ???
سلام ببخشید چطوری میتونید عکسی یا فیلمی را داخل گوگل بذارید؟
با سلام
سرچ کنید به جواب خودتون میرسید
ممنون واقعا عالی بود ???
با سلام وسپاس
خدا رو شکر
سلام عالی بود لطفا در مورد شکل های هم نهشت هم توضیح بدید
خیلی خیلی ممنون
با سلام ممنون از نظر شما
ممنون از زحمت شما
خوب بود، قابل فهم توضیح داده شده بود. ممنون.
واقعا عالی بود
با سلام دوست عزیز
ممنون از لطف شما
2
عالی بود
با سلام دوست عزیز
سپاس از لطف شما
اوکیه
خدا رو شکر
عاااااالی
سپاس
چقدر خوب توضیح میدید.
عالی بود ممنون
سلام دوست عزیز
ممنون از نظر لطف شما
خیلی ممنونم واقعا به دردم خورد
عالی، ممنون، هیجا این جوری توضیح نمیدن
با سلام وادب
ممنون از نظر شما ما اختصاصی روی کتابهای ریاضی وقت گذاشتیم تا به زبان ساده آنها را بیان کنیم
سلام ایا در دوران 180 جهت شکل تغییر میکند
بله کاملا جهت عوض میشه مثال داخل پیت رو ببینید
خیلی عالي
با سلام و ادب
بله کاملا جهت عوض میشه ۱۸۰ درجه میچرخه مثال داخل پست رو ببینید
خیلی عالی بود، من فردا امتحان هم دارم واقعا به دردم خورد🙏🏻
با سلام خوشحالیم که مفید واقع شده
سلام من یه سوال داشتم ممنون میشم جواب بدید
کوچک و بزرگ کردن شکل جز ٕ. تبدیلات شکل میشن یا نه
مثلا وقتی یه شکلی رو با همون تناسب اندازه کوچک تر یا بزرگ تر میکنیم یعنی ما شکل اول رو به شکل بعدی تبدیل کردیم یا به این کار تبدیل نمیگن ؟
با سلام دوست عزیز
وقتی شکلی بزرگ یا کوچک میشه شکلهای متشابه به وجود میاد ودر هندسه مورد بررسی قرار میگیره
الحمدللّه
بسیار عالی و فراتر از عالی بود
پروردگار رحمان خیر دنیا و آخرتتان دهد
با سلام
ممنون از شما دوست عزیز
سلام خیلی خیلی عالی بود