مقدار عددی یک عبارت جبری هفتم 🔁〽️- جاگذاری عدد با متغیر‌!

 در درسنامۀ مقدار عددی یک عبارت جبری هفتم می‌خواهیم با قرار دادن اعداد به جای متغیر‌ها در عبارت‌های جبری، مقدار عددی آن‌ها را بیابیم. در صورتی که فراموش کرده‌اید که عبارت‌های جبری چه عبارت‌هایی هستند، حتماً قبل از مطالعۀ این درسنامه، درسنامۀ عبارت‌های جبری هفتم را مرور کنید. سعی می‌کنیم با حل مثال‌های متنوع، این مبحث کتاب را فرا بگیریم. با ما تا انتها همراه باشید.

مثال از الگوهای عددی

مثال 1: با توجه به شکل‌های زیر، ابتدا تعداد مربع‌ها در شکل چهارم را به دست آورده و شکل چهارم را رسم کنید. سپس، تعداد مربع‌های شکل \(\Large n\)ام را به دست آورده و با استفاده از آن، تعداد مربع‌های شکل چهل‌ام را محاسبه کنید.

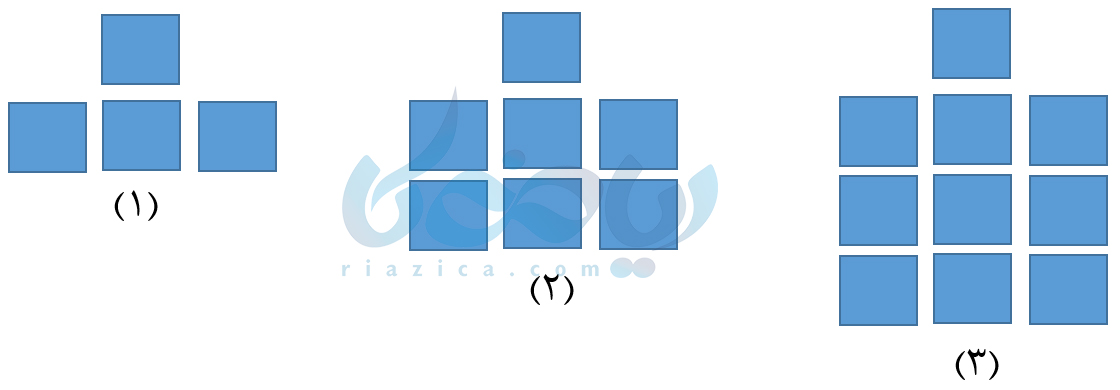
حل: در این مثال از درسنامۀ مقدار عددی یک عبارت جبری هفتم می‌توانیم هر شکل را به صورت زیر دسته بندی کنیم:

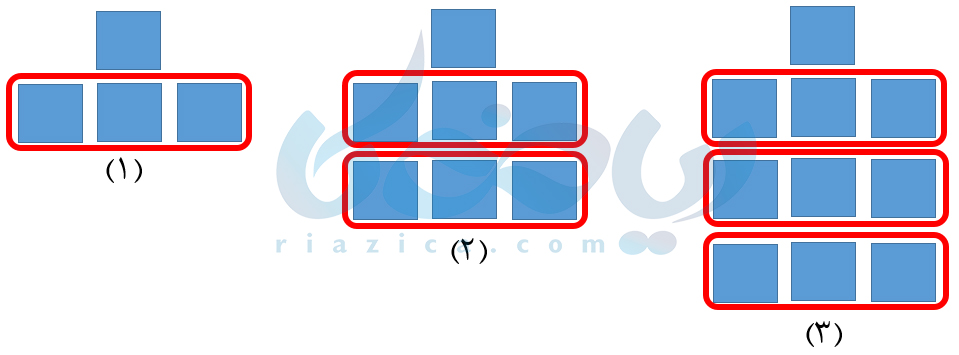
بنابراین در شکل اول، \(\Large 1\times 3+1\) مربع، در شکل دوم، \(\Large 2\times 3+1\) مربع و در شکل سوم، \(\Large 3\times 3+1\) مربع وجود دارد. در نتیجه می‌توان گفت در شکل چهارم نیز، \(\Large 4\times 3+1\) مربع وجود خواهد داشت:

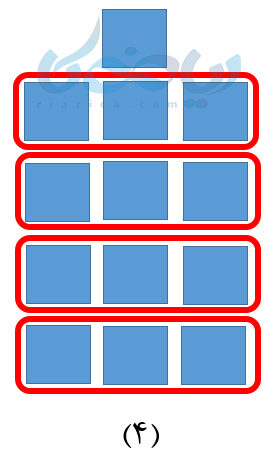
در نتیجه تعداد مربع‌ها در شکل \(\Large n\)ام، که به آن جملۀ \(\Large n\)ام نیز می‌گوییم، برابر با \(\Large 3\times n+1\) خواهد بود. برای به دست آوردن تعداد مربع‌ها در شکل چهل‌ام کافی است عدد \(\Large 40\) را به جای \(\Large n\) قرار دهیم. در نتیجه تعداد مربع‌ها در شکل چهل‌ام، برابر است با \(\Large 40\times 3+1\) یعنی \(\Large 121\). همان‌طور که دیدید، با قرار دادن عدد \(\Large 40\) به جای \(\Large n\) مقدار عددی یک عبارت جبری را به دست آوردیم. به مثال بعدی از درسنامۀ مقدار عددی یک عبارت جبری هفتم توجه کنید.

مثال از محاسبۀ محیط

مثال 2: مربعی به شکل زیر داریم. ابتدا یک عبارت جبری برای محاسبۀ محیط آن بنویسید. سپس مشخص کنید اگر \(\Large a=5\) باشد، محیط مربع چه قدر است.

حل: محیط یک مربع برابر است با چهار برابر ضلعش. بنابراین اگر محیط مربع را با \(\Large P\) نشان دهیم، داریم:

\(\LARGE P=4a\)

این همان عبارت جبری است که مسئله از ما خواسته بود. حال اگر به جای \(\Large a\) عدد \(\Large 5\) را قرار دهیم، محیط مربع برابر است با:

\(\LARGE P=4\times 5=20\)

در این مثال نیز، با قرار داردن یک عدد به جای متغیر، مقدار عبارت جبری را به دست آوردیم. به مثال بعدی از درسنامۀ مقدار عددی یک عبارت جبری هفتم توجه کنید.

مثال از محاسبۀ هزینۀ کتاب

مثال 3: می‌خواهیم از یک فروشگاه، \(\Large m\) خودکار و \(\Large n\) مداد تهیه کنیم. اگر هزینۀ هر خودکار \(\Large 5000\) تومان و هر مداد \(\Large 4000\) تومان باشد، آنگاه:

• یک عبارت جبری برای مجموع هزینه‌ای که باید بپردازیم بنویسید.
• اگر تعداد خودکار خریده شده برابر با \(\Large 3\) و تعداد مداد خریداری شده برابر با \(\Large 6\) باشد، مجموع هزینه را محاسبه کنید.

حل: هزینۀ \(\Large m\) خودکار برابر است با \(\Large m\times 5000\) تومان. هزینۀ \(\Large n\) مداد نیز برابر است با \(\Large n\times 4000\) تومان. بنابراین مجموع هزینه‌ای که باید بپردازیم برابر است با:

\(\LARGE m\times 5000+n\times 4000\)

برای حل قسمت دوم این مثال از درسنامۀ مقدار عددی یک عبارت جبری هفتم کافی است به جای \(\Large m\) عدد \(\Large 3\) و به جای \(\Large n\) عدد \(\Large 6\) قرار دهیم. در این صورت، مجموع هزینه برابر است با:

\(\LARGE 3\times 5000+6\times 4000\)

\(\LARGE =15000+24000\)

\(\LARGE =39000\)

مثال از محاسبۀ مقدار عددی عبارت جبری

مثال 4: مقدار عددی عبارت جبری \(\Large 3(2x-4y)-5x\) را به ازای \(\Large x=2\) و \(\Large y=3\) به دست آورید.

حل: هم می‌توانیم از ابتدا به جای متغیرهای \(\Large x\) و \(\Large y\)، اعداد \(\Large 2\) و \(\Large 3\) را جایگزین کنیم. هم می‌توانیم ابتدا عبارت داده شده را ساده کرده و در انتها اعداد را جاگذاری کنیم. پیشنهاد می‌کنیم ابتدا عبارت را ساده کرده، سپس اعداد را جاگذاری کنید. برای ساده سازی عبارت داده شده داریم:

\(\LARGE 3(2x-4y)-5x\)

\(\LARGE =6x-12y-5x\)

\(\LARGE =x-12y\)

حال عدد \(\Large 2\) را به جای متغیر \(\Large x\) و عدد \(\Large 3\) را به جای متغیر \(\Large y\) جاگذاری می‌کنیم:

\(\LARGE 2-12\times 3\)

\(\LARGE =2-36\)

\(\LARGE =-34\)

برای خوندن ادامه  مطلب به پست  معادله ریاضبی هفتم مراجعه کنید.

زنگ آخر کلاس مقدار عددی یک عبارت جبری هفتم

در این درسنامه سعی کردیم تا با حل مثال‌های مختلف، نحوۀ جاگذاری اعداد به جای متغیر‌ها و محاسبۀ مقدار عددی عبارت‌های حبری را نشان دهیم. همان‌طور که در ابتدای درسنامه نیز توصیه کردیم، برای درک بهتر این درسنامه حتماً درسنامۀ عبارت‌های جبری را مرور کنید.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث مقدار عددی یک عبارت جبری هفتم دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.