آموزش ریاضی پایه هفتم
روابط بین پاره خط ها ریاضی هفتم 📏⚙️ – دنبال رابطشون باش!
در درسنامۀ روابط بین پاره خط ها ریاضی هفتم به مباحث زیر میپردازیم:
- نامگذاری خط و نقطه
- نمایش طول پاه خط ها
- مقایسۀ طول پاره خط ها و روابط بین آنها
مبحث بسیار سادهای است! در عین حال سعی میکنیم با حل مثالهای مختلف، تمام جوانب آن را بررسی کنیم. با ما تا انتهای درسنامه همراه باشید.
نامگذاری خط و نقطه
اولین مبحث از درسنامۀ روابط بین پاره خط ها ریاضی هفتم ، روش نام گذاری خط و نقطه است. قبل آزموزش نام گذاری خط ونقطه باید متذکر شویم خط از دو طرف امتداد دارد ولی نیم خط از یک طرف بسته است وپاره خط از دو طرف بسته است .معمولاً نقاط را با حروف بزرگ انگلیسی نمایش میدهیم. برای نشان دادن خطوط نیز از حروف کوچک انگلیسی استفاده می کنیم. برای نشان دادن امتداد یک خط از فلش استفاده میکنیم. چون خط از دو طرف امتداد دارد دو طرف خط فلش می گذاریم و با یک یا دو حرف کوچک آن را نشان می دهیم و در مورد نیمخط چون یک طرف بسته یا همان نقطه است یک طرف حرف بزرگ ویک طرف حرف کوچک وپاره خط چون دو طرفش بسته است دو سرش را با حرف بزرگ نام گذاری میکنیم در شکل زیر میتوانید نکاتی را که گفتیم، مشاهده کنید:
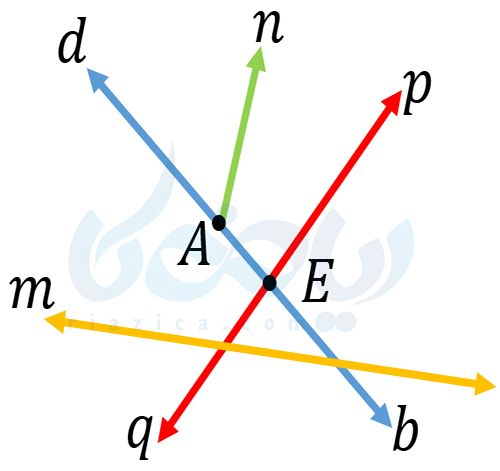
به مثال بعدی از درسنامۀ روابط بین پاره خط ها ریاضی هفتم توجه کنید.
مثال از نامگذاری خط و نقطه
مثال 1: در شکل زیر، نام خط ها، نیم خط ها و پاره خط ها را بنویسید.
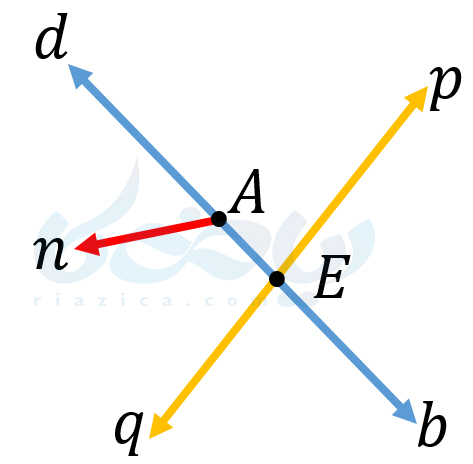
حل: برای اینکه نام هیچ خط، پاره خط و یا نیم خطی از قلم نیفتد، باید نام گذاری را منظم انجام دهیم. مثلاً از بالای شکل شروع کرده و هر حرفی که میبینیم، خط ها، پاره خط ها و نیم خط های متناظر با آن را مینویسیم (به این روش منظم، به اصطلاح کتاب، راهبرد الگوسازی میگوییم. در درسنامۀ راهبردهای حل مسئله، این راهبرد را بررسی کردیم). در هر مرحله که پایین تر میرویم، خط ها، پاره خط ها و نیم خط های بالایی را در نظر نمیگیریم.
در اولین گام از حل این مثال از درسنامۀ روابط بین پاره خط ها ریاضی هفتم ، حرف \(\Large d\) را در نظر میگیریم. برای حرف \(\Large d\)، نیم خط های \(\Large Ad\) و \(\Large Ed\) و خط \(\Large bd\) را داریم (خطوط را می توانیم با یک حرف نیز نمایش دهیم). برای حرف \(\Large p\)، نیم خط \(\Large Ep\) و خط \(\Large pq\) را داریم. برای حرف \(\Large A\) نیم خط های \(\Large An\) و \(\Large Ab\) وپاره خط \(\Large AE\) وجود دارد. برای حرف \(\Large n\)، نیم خط جدیدی نداریم. برای حرف \(\Large E\)، دو نیم خط \(\Large Eb\) و \(\Large Eq\) را داریم. برای حرفهای \(\Large b\) و \(\Large q\) نیز، خط، نیم خط یا پاره خط جدیدی نداریم. حال میتوانیم تمام خط ها، نیم خط ها و پاره خط ها را در جدول زیر نشان دهیم:

نمایش طول پاره خط
در قسمت دوم درسنامۀ روابط بین پاره خط ها ریاضی هفتم ، روش نمایش طول پاره خط ها را بررسی میکنیم. طول هر پاره خط را با قرار دادن یک پاره خط کوچک بالای آن نمایش میدهیم. مثلاً طول پاره خط \(\Large AB\) را با \(\Large \overline{AB}\) نمایش میدهیم.
مثال 1: در شکل زیر، \(\Large \overline{AC}-\overline{BC}\) برابر با طول کدام پاره خط است؟
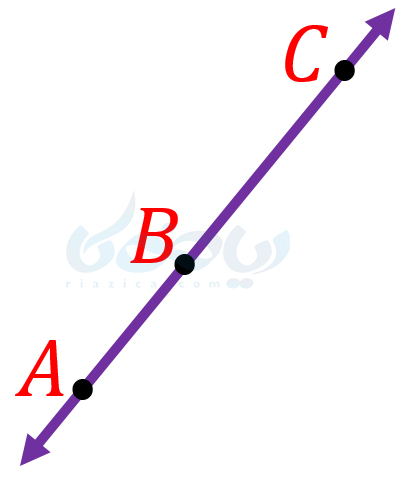
حل: اگر طول پاره خط \(\Large BC\) را از طول پاره خط \(\Large AC\) کم کنیم، طول پاره خط \(\Large AB\) حاصل میشود. یعنی داریم:
\(\LARGE \overline{AC}-\overline{BC}=\overline{AB}\)
مقایسۀ طول پاره خط ها
طول پاره خط ها را میتوان با یکدیگر مقایسه کرد. یعنی میتوان بررسی کرد که طول کدام یک از دیگری بزرگتر، کوچکتر و یا با دیگری برابر است. در هر یک از قسمتهای بعدی از درسنامۀ روابط بین پاره خط ها ریاضی هفتم به مقایسۀ طول پاره خط ها می پردازیم.
نامساوی مثلثی
شکل زیر را در نظر بگیرید:
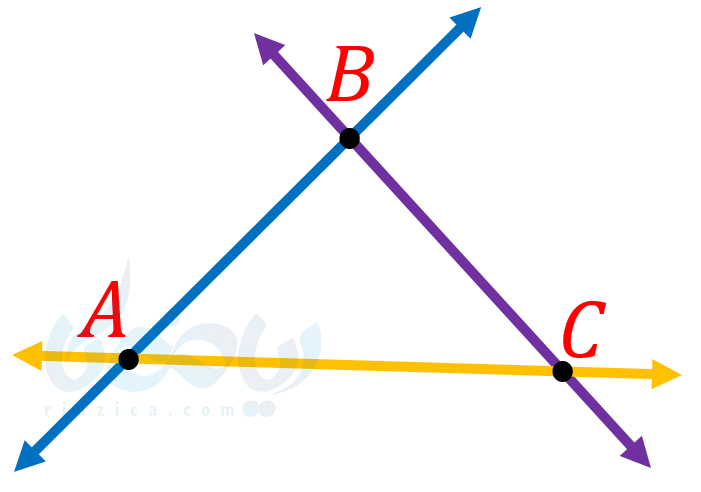
نقاط \(\Large A\) و \(\Large B\) و \(\Large C\) تشکیل مثلث \(\Large ABC\) میدهند. مثلث \(\Large ABC\) را با نماد \(\Large \Delta ABC\) یا \(\Large A\overset{\Delta}{B}C \) نمایش میدهیم. در هر مثلثی، مجموع طول دو ضلع، بزرگتر از طول ضلع سوم است. به این نامساوی، نامساوی مثلثی میگوییم. به طور مثال در مثلث \(\Large ABC\) در شکل بالا، این نامساوی را با روابط زیر نشان میدهیم:
\(\LARGE \overline{AB}+\overline{BC}>\overline{CA}\)
\(\LARGE \overline{BC}+\overline{CA}>\overline{AB}\)
\(\LARGE \overline{CA}+\overline{AB}>\overline{BC}\)
در درسنامۀ روابط بین پاره خط ها ریاضی هفتم به اثبات این نامساوی نمیپردازیم. اما باید خاطر نشان کرد که این نامساوی کاربردهای زیادی در بخشهای مختلف ریاضی دارد.
مثال از نامساوی مثلثی
مثال 2: در شکل زیر \(\Large \overline{AB}=2\) و \(\Large \overline{BC}=3\) است. اگر \(\Large \overline{CA}\) برابر با عددی طبیعی باشد، مقدار آن حداکثر چند است؟
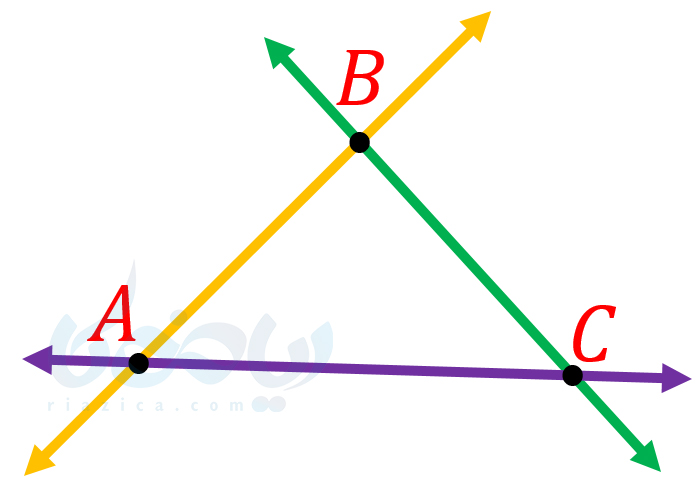
حل: طبق نامساوی مثلث داریم:
\(\LARGE \overline{AB}+\overline{BC}>\overline{CA}\)
\(\LARGE \Rightarrow 2+3>\overline{CA}\)
\(\LARGE \Rightarrow 5>\overline{CA}\)
بنابراین \(\Large \overline{CA}\) از \(\Large 5\) کمتر است. از آنجاییکه طبق فرض مسئله، \(\Large \overline{CA}\) عددی طبیعی است، بنابراین \(\Large \overline{CA}\) حداکثر \(\Large 4\) است. به قسمت بعدی از درسنامۀ روابط بین پاره خط ها ریاضی هفتم توجه کنید.
برابری دو پاره خط
برای نشان دادن برابری دو پاره خط در یک شکل، معمولاً روی هر کدام از آنها یک یا چند پاره خط کوچک قرار میدهیم. مثلاً به شکل زیر نگاه کنید:
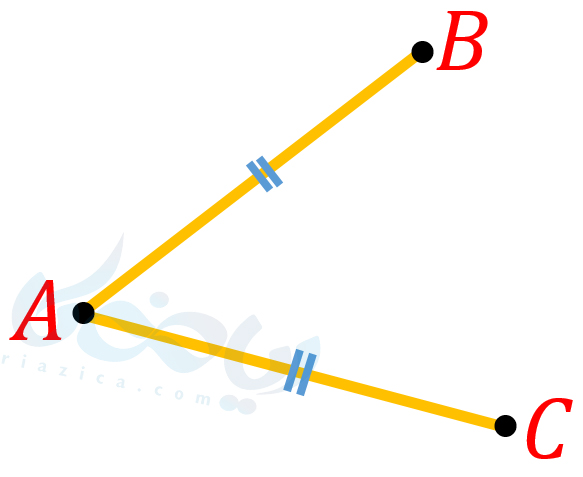
در شکل بالا، \(\Large \overline{AB}=\overline{AC}\). در ادامۀ این درسنامه مثالهایی از برابری پاره خط ها حل خواهیم کرد.
مثال از برابری پاره خط ها در روابط بین پاره خط ها ریاضی هفتم
مثال 3: در شکل زیر، \(\Large ABCD\) مربع و \(\Large ABE\) مثلث متساوی الاضلاع است. ثابت کنید \(\Large \overline{AE}=\overline{CD}\).
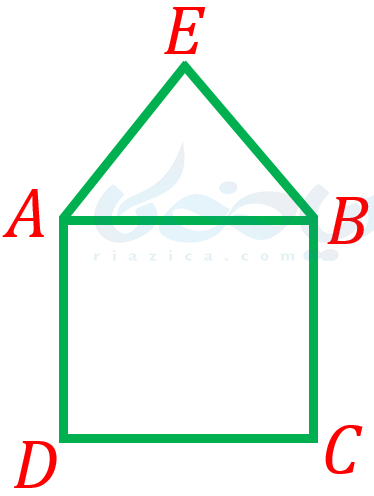
حل: از آنجاییکه \(\Large ABE\) مثلث متساوی الاضلاع است، طول تمام اضلاع آن با هم برابر است. بنابراین داریم:
\(\LARGE \overline{AE}=\overline{AB}\)
از طرفی چون \(\Large ABCD\) مربع است، طول تمام اضلاع آن نیز با هم برابر است. بنابراین داریم:
\(\LARGE \overline{CD}=\overline{AB}\)
از آنجاییکه \(\Large \overline{AE}\) با \(\Large \overline{AB}\) برابر است، \(\Large \overline{CD}\) هم با \(\Large \overline{AB}\) برابر است، نتیجه میگیریم \(\Large \overline{AE}\) با \(\Large \overline{CD}\) برابر است. آنچه که گفتیم را میتوان به صورت خلاصه به شکل زیر نوشت:
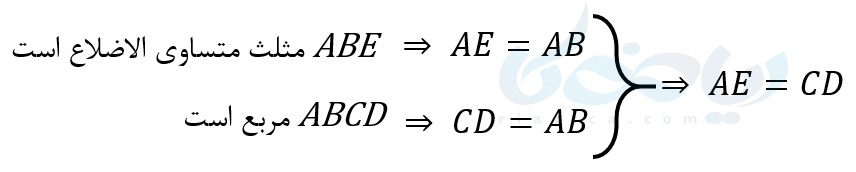
به مثال بعدی از این درسنامه توجه کنید.
مثال از تفاضل طول پاره خط ها در روابط بین پاره خط ها ریاضی هفتم
مثال 4: در شکل زیر، \(\Large \overline{AB}=\overline{DE}\) و \(\Large \overline{BD}=2\overline{DE}\). مقدار \(\Large \overline{AD}+\overline{BE}\) چند برابر \(\Large \overline{DE}\) است؟
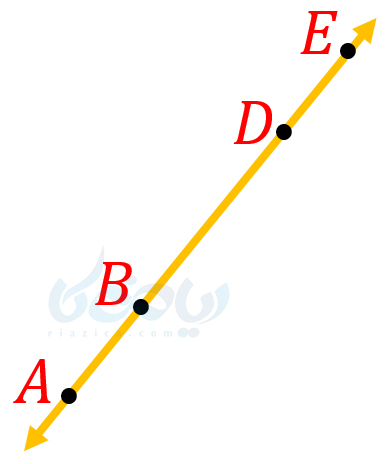
حل: همان طور که از شکل پیداست، برای \(\Large \overline{AD}\) داریم:
\(\LARGE \overline{AD}=\overline{AB}+\overline{BD}\)
\(\LARGE \Rightarrow \overline{AD}=\overline{DE}+2\overline{DE}\)
\(\LARGE \Rightarrow \overline{AD}=3\overline{DE}\)
از طرفی برای \(\Large \overline{BE}\) داریم:
\(\LARGE \overline{BE}=\overline{BD}+\overline{DE}\)
\(\LARGE \Rightarrow \overline{BE}=2\overline{DE}+\overline{DE}\)
\(\LARGE \Rightarrow \overline{BE}=3\overline{DE}\)
بنابراین میتوان نتیجه گرفت:
\(\LARGE \overline{AD}+\overline{BE}\)
\(\LARGE =3\overline{DE}+3\overline{DE}\)
\(\LARGE =6\overline{DE}\)
برای خوندن ادامه مطلب به پست روابط بین زاویه ها مراجعه کنید
زنگ آخر کلاس روابط بین پاره خط ها ریاضی هفتم
در درسنامهای که از ریاضی هفتم خواندیم، با نحوۀ نمایش خط و نقطه و همچنین طول پاره خط آشنا شدیم. طول پاره خط ها را با یکدیگر بررسی کرده و مثالهای مختلفی از آن حل کردیم. همان طور که دیدیم، مقایسۀ طول پاره خط ها در قضیۀ نامساوی مثلثی که یکی از قضایای مهم ریاضی است، وهمچنین در مسائل مختلف، به کار میرود.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با این مبحث دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





سلام و وقت بخیر.ممنونم از توضیحات تون.ولی خیلی خوب میشه اگر آموزش ها به صورت رایگان باشه.من همیشه اعتقاد عجیبی به بیت بی نظیر تو نیکی میکن و در دجله انداز
که ایزد در بیابانت دهد باز.
با سلام وادب
دوست عزیز اینهمه آموزش رایگان داریم باید خرج سایت در بیاد یا نه بعدهم تا کسی برا آموزشی که میبینه پول نده ارزشش رو درک نمیکنه شما یه آدامس هم مجانی نمیتونی بخری
دوست عزیز تمام درسنامه های روی سایت رایگان می باشد که وقت وهزینه زیادی صرف نوشتن اونها شده ودائم در حال بروزرسانی مطالب هستیم
سلام عالیه ممنون دستتون درد نکنه
با سلام و ادب
خواهش میکنم خرسندیم استفاده کردید
خیلی در عین سادگی سخته این درس
سلام دوست عزیز با تکرار وتمرین هر راه سختی آسون میشه
سلام میشه مثال های دیگه هم بزنید و حل کنید ؟
سایت خیلی خوبی دارید ممنون ?
با سلام وادب
ممنون از نظر شما حتما در آینده نزدیک
عالی
سلام خیلی خوب بود ممنون👌🏻❤
روش حل عبارت جبری از دو روش 1خلاصه و2تبدیل توضیح بدین ممنون
سلام دوست عزیز اینجا توضیحش سخته میتونید در کلاسهای آنلاین به صورت خصوصی شرکت کنید وجواب سوالاتتون رو بگیرید
خیلی خوب نیست و من جواب سوالات را نوشتم و به چهار تا از معلم ریاضی مختلف پرسیدم و همه ای جواب ها غلط است
چه سوالاتی ؟
عالییی ممنون بابت توضیحاتتون💙
سلام میشه روابط بین پاره خط ها و توضیح بدی یعنی چی؟
واقعا سایت خیلی خوب با توضیحات خوبی دارید
واقعا عالی بود
سلام ممنون از نظر شما
عالی بود