آموزش ریاضی پایه هفتم
الگوهای عددی ریاضی هفتم 🔰5️⃣- با متغیرها مثل اعداد رفتار کن!
در درسنامۀ الگوهای عددی ریاضی هفتم ابتدا مرور کوتاهی میکنیم بر مبحث الگوهای عددی که از سالهای پیش با آن آشنایی دارید. سپس به سوالات زیر پاسخ میدهیم:
- جبر چیست؟
- متغیر در جبر چه معنایی دارد؟
- قوانین ریاضی به زبان جبر چگونه نوشته می شوند؟
سعی میکنیم از مثالهای متنوع برای درک بهتر درس الگوهای عددی ریاضی هفتم کمک بگیریم تا این مبحث را به خوبی فرا بگیرید.
الگوی عددی شکل nام
در هر الگوی عددی تعدادی شکل یا عدد وجود دارد که ما باید با توجه به رابطۀ بین آنها، شکلها یا عددهای بعدی را تعیین کنیم. گاهی نیز باید یک رابطۀ کلی برای شکل یا عدد nام تعیین کنیم. به مثال زیر از مبحث الگوهای عددی ریاضی هفتم دقت کنید.
مثال از الگوی دایرهها
مثال 1: با توجه به شکلهای زیر والگوی موجود در آنها، شکلهای چهارم و پنجم را رسم و جدول زیر را کامل کنید.
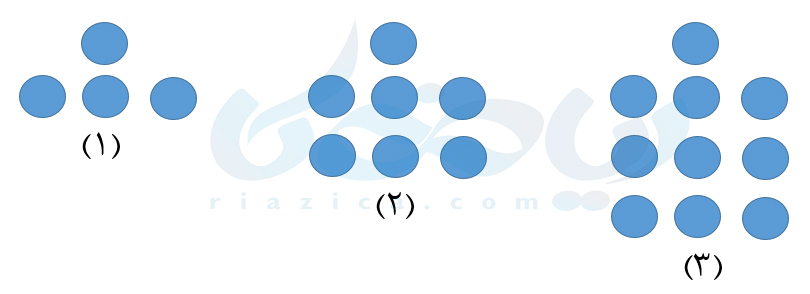

حل: اگر دقت کنید، در هر شکل تعدادی دستۀ سه تایی وجود دارد:
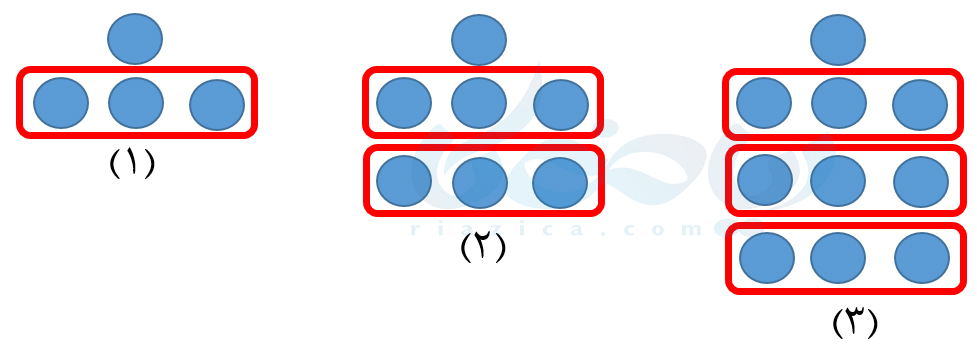
بنابراین در شکل اول، \( \Large 1\times 3+1\) دایره، در شکل دوم، \( \Large 2\times 3+1\) دایره و در شکل سوم \( \Large 3\times 3+1 \) دایره وجود دارد. بنابراین در شکل چهارم، \( \Large 4\times 3+1\) دایره و در شکل پنجم، \( \Large 5\times 3+1\) دایره وجود خواهد داشت. بنابراین شکل چهارم و پنجم به صورت زیر خواهد بود:
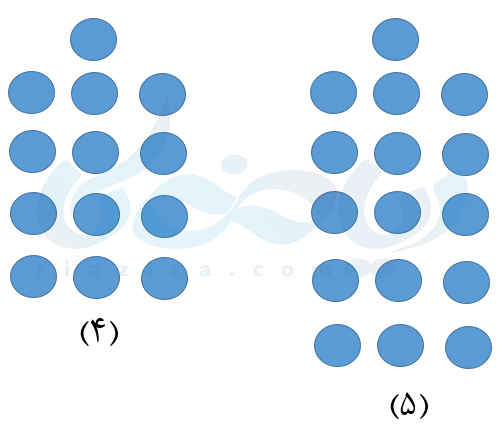
همچنین، با توجه به الگویی که یافتیم، جدول داده شده در مسئله، به صورت زیر کامل میشود:

دقت کنید در جدول بالا به جای \( \Large n\) هر عددی میتوانیم قرار دهیم. به طور مثال اگر \( \Large n\) را \( \Large 20\) بگذاریم، تعداد دایرههای شکل بیستم برابر با \( \Large 20\times 3+1\) یعنی \( \Large 61\) میشود. به مثال بعدی از مبحث الگوهای عددی ریاضی هفتم دقت کنید.
مثال از تعداد مربعها
مثال 2: با توجه به شکلهای زیر والگوی موجود در آنها، شکلهای چهارم و پنجم را رسم و جدول زیر را کامل کنید.
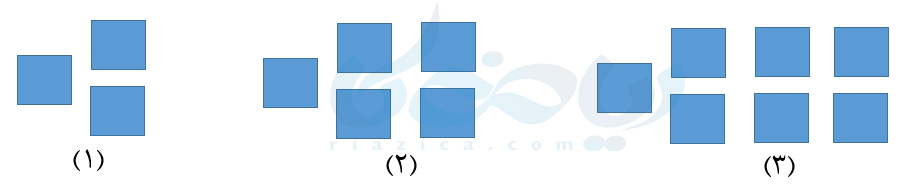
حل: اگر دقت کنید، در هر شکل تعدادی دستۀ دو تایی وجود دارد:
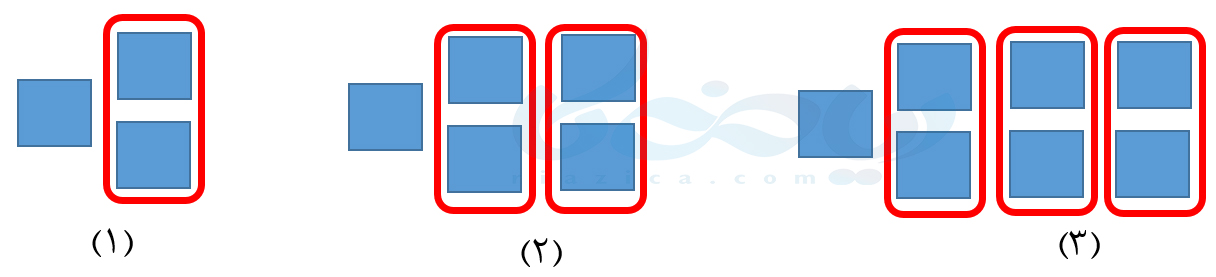
بنابراین در شکل اول، \( \Large 1\times 2+1\) دایره، در شکل دوم، \( \Large 2\times 2+1\) دایره و در شکل سوم \( \Large 3\times 2+1 \) دایره وجود دارد. بنابراین در شکل چهارم، \( \Large 4\times 2+1\) دایره و در شکل پنجم، \( \Large 5\times 2+1\) دایره وجود خواهد داشت. بنابراین شکل چهارم و پنجم به صورت زیر خواهد بود:
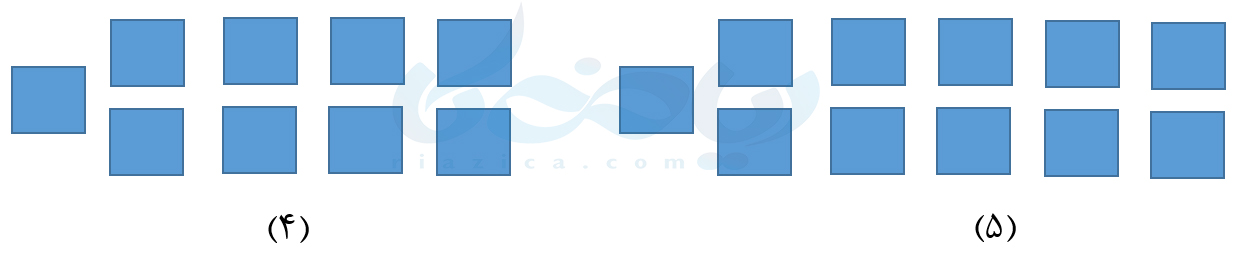
همچنین، با توجه به الگویی که یافتیم، جدول داده شده در مسئله، به صورت زیر کامل میشود:

به مثال بعدی از مبحث الگوهای عددی ریاضی هفتم دقت کنید.
مثال از الگوی اعداد
مثال 3: جملۀ \( \Large n\)ام الگوی عددی زیر را بیابید.
\( \LARGE \frac{2}{3}, \frac{4}{5}, \frac{6}{7}, \dots\)
حل: کسر اول برابر است با \( \Large \frac{2 \times 1}{2 \times 1+1}\)، کسر دوم برابر است با \( \Large \frac{2 \times 2}{2 \times 2+1}\) و کسر سوم برابر است با \( \Large \frac{2 \times 3}{2 \times 3+1}\). در نتیجه میتوان گفت کسر \( \Large n\)ام برابر است با \( \Large \frac{2 \times n}{2 \times n+1}\). جملۀ \( \Large n\)ام در هر الگو برای ما بسیار با ارزش است؛ زیرا به وسیلۀ آن میتوانیم هر جمله از دنباله را که بخواهیم به دست آوریم. مثلاً در همین الگو اگر جملۀ سیام را از ما میخواستند، با توجه به جملۀ \( \Large n\)ام میتوانستیم بگوییم جملۀ سیام برابر است با \( \Large \frac{2 \times 30}{2 \times 30+1}\) که همان \( \Large \frac{60}{61}\) است. حال با حل این مثالها، در قسمت بعدی از درسنامۀ الگوهای عددی ریاضی هفتم ، با جبر و مفهوم متغیر آشنا خواهیم شد.
جبر چیست؟ متغیر در جبر چه معنایی دارد؟
واژۀ “جبر” یا “Algebra” برگرفته از عنوان کتاب “المختصر فی حساب الجبر و المقابله” نوشتۀ خوارزمی، دانشمند ایرانی است. میتوان گفت جبر قبل از این کتاب ارزشمند خوارزمی وجود نداشت و به وسیلۀ او پدید آمد. اما جبر چیست؟ پاسخ به این سوال با توجه به معلوماتی که تا به اینجا کسب کردهایم دشوار است، اما میتوان گفت در جبر با اشیای مجهول و روابط بینشان سر و کار داریم. به این اشیای مجهول، متغیر میگوییم. برای اینکه بهتر متوجه شوید، مثال 2 را در نظر بگیرید. همانطور که در مثال 2 محاسبه کردیم، جملۀ \( \Large n\)ام برابر با \( \Large \frac{2 \times n}{2 \times n+1}\) است. اما \( \Large n\) چیست؟ \( \Large n\) هر عددی میتواند باشد. در واقع \( \Large n\) یک عدد نامعلوم است. همانطور که گفتیم، \( \Large n\) را متغیر مینامیم. در این مثال به جای \( \Large n\) هر عددی طبیعی میتوانیم قرار دهیم. برای اینکه با متغیر و عبارتهای جبری بیشتر آشنا شوید، به مثالهای بعدی از درسنامۀ الگوهای عددی ریاضی هفتم دقت کنید.
مثال از پیدا کردن محیط و مساحت با استفاده از متغیر
مثال 4: مربعی به شکل زیر داده شده است که هر ضلع آن برابر با \( \Large a\) است. محیط و مساحت آن را به دست آورید.

حل: محیط یک مربع برابر است با چهار برابر ضلع آن. بنابراین محیط این مربع برابر است با:
\( \LARGE P=4\times a\)
مساحت یک مربع برابر است با اندازۀ یک ضلع ضرب در خودش. بنابراین مساحت این مربع برابر است با:
\( \LARGE S=a\times a\)
دیدید چه ساده بود! با متغیرها مانند اعداد برخورد میکنیم. به مثال بعدی از درسنامۀ الگوهای عددی ریاضی هفتم توجه کنید.
مثال از جمع متغیرها با اعداد در الگوهای عددی ریاضی هفتم
مثال 5: ابتدا توضیح دهید که در نمودار زیر چه اتفاقی میافتد. سپس آن را کامل کنید.
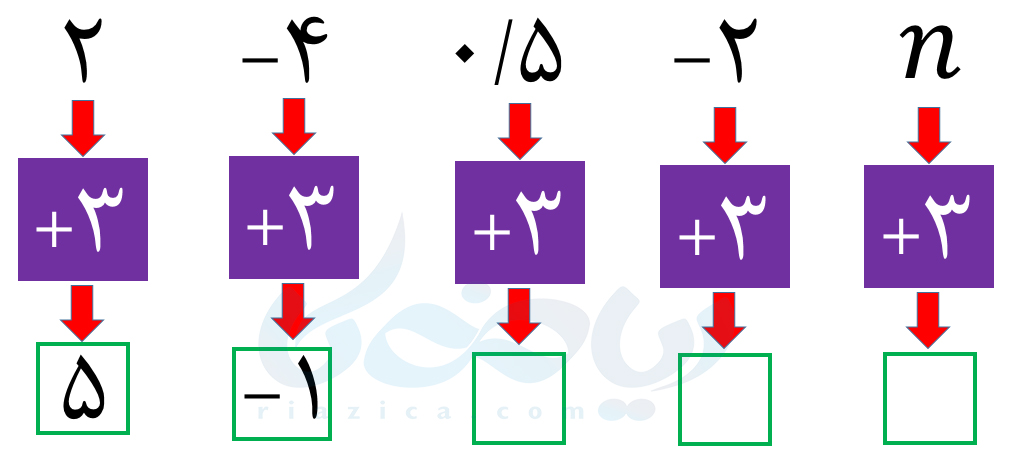
حل: همانطور که میبینید، هر عددی که وارد مربع میشود، با عدد 3 جمع شده و از مربع خارج میشود. بنابراین برای بقیۀ اعداد و همچنین متغیر n نیز باید همین کار را انجام دهیم. در این صورت نمودار به صورت زیر کامل میشود:
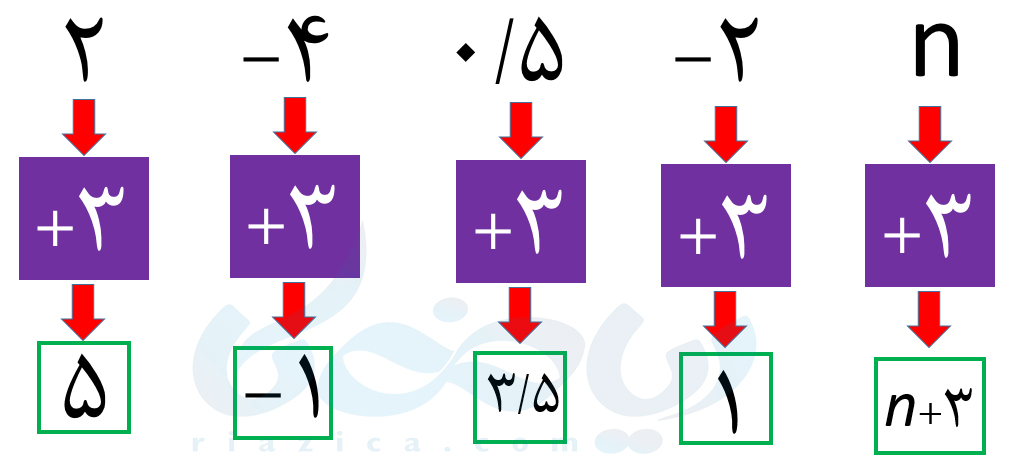
به مثال بعدی از درسنامۀ الگوهای عددی ریاضی هفتم توجه کنید.
مثال از حل مسئله از متغیرها در الگوهای عددی ریاضی هفتم
مثال 6: در یک آشفروشی، قیمت هر ظرف، 2000 تومان و قیمت هر کیلو آش، 15000 تومان است. اگر \( \Large n\) کیلو آش با ظرف بخریم، باید چه قدر پول بپردازیم؟
حل: قیمت \( \Large n\) کیلو آش برابر است با \(\Large n \times 15000\)، قیمت ظرف هم که\( \Large 2000\) تومان است. بنابراین قیمت کل برابر است با مجموع این دو، یعنی \( \Large n \times 15000+2000\).
قوانین ریاضی به زبان جبر
در مجموعههای اعداد، برای اعمال مختلف، خواص مختلفی وجود دارد. مثلاً در مجموعۀ اعداد صحیح، عمل ضرب خاصیت جابجایی دارد. یا مثلاً در مجموعۀ اعداد صحیح، برای عمل جمع عضو وارون (قرینه) داریم. به طور کلی مجموعههای مختلف با توجه به عملی که روی آنها تعریف میشود، دارای خواص مختلفی هستند که میتوانیم هر یک از این خواص را به صورت جبری نشان دهیم. مثلاً برای نشان دادن خاصیت جابجایی جمع در اعداد صحیح میتوانیم بنویسیم، به ازای هر \( \Large a\) و \( \Large b\) دلخواه که عضو مجموعۀ اعداد صحیح باسند، خاصیت زیر برقرار است:
\(\LARGE a\times b=b\times a\)
از عبارتهای جبری میتوان برای نشان دادن این خواص استفاده کرد.
در ادامه پست عبارتهای جبری هفتم رو مطالعه کنید.
زنگ آخر کلاس الگوهای عددی ریاضی هفتم
به پایان درسنامۀ الگوهای عددی ریاضی هفتم رسیدیم. این درسنامه مقدمهای بود برای آشنایی با عبارتهای جبری که در درسنامههای بعدی با آن آشنا خواهیم شد. همانطور که دیدید میتوان با متغیرها مانند اعداد رفتار کرد و عبارتهای جبری را تشکیل داد. حل و مرور مثالهای این درسنامه، کمک زیادی به درک مبحث و تسلط شما میکند.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث الگوهای عددی ریاضی هفتم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





خیلی خوب بود واقعاً توضیحات مفید و جامع بود?
سلام ممنون ازتون. خواهش میکنم.
عااااااالی بود
ممنون دوست عزیز
خوب بود ولی کاش
جملات متاشبه و معادله رو داشت مینوشتم جزوه رو کامل میکردم?❣️
سلام و عرض ادب
ممنون از توجهتون
برای جملات متشابه:
https://riazica.com/algebraic-expressions/
و برای معادله:
https://riazica.com/equation/
به این لینک ها بروید.
موفق باشید.
عالی
سلام
ممنون از اینکه سایت ما رو انتخاب کردید.
موفق باشید.
از کجا بفهمیم که باید به صورت جبری حل کنیم ؟؟؟
ضمن عرض سلام
اکثر سوالات ریاضی را میشود از راه حل جبری و با تشکیل معادله حل کرد. و میتوان گفت که به تعداد افرادی که یک مسئله را حل میکنند، مسئله میتواند راه حل داشته باشد.
اشتراکها: علی
سلام و عرض ادب
ممنون از انرژی و پیام پرمهرتون.
موفق باشید.
پیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
اشتراکها: زینب
با سلام وعرض ادب
خدا رو شکر که براتون مفید بوده
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام
میشه به این سوال پاسخ بدین
جمله n ام ، ۳-2n مقدار عددی جمله سیزدهم را محاسبه کنید . ممنون??
با سلام ووقت به خیر
خیلی ساده کافیه به جای ان سیزده بذارید
سلام وقت بخیر
ممنون میشم در یافتن الگوی این اعداد کمکم کنید
1،7،14،…
با عرض سلام میشه عدد های جبری را بهم کمک کنین؟
با سلام
چه کمکی
سلام خسته نباشید ببخشید مثلا اگه عدد بالای صد بود ما که نمیتونیم واسش شکل بکشیم باید چیکار کنیم؟
با سلام
منظورتون رو با یه نمونه سوال بیان کنید
سلام ممنونم خیلی فهمیدم
با سلام وادب
خدا رو شکر
سلام ممنون خیلی مفید و کاربردی بود
با سلام
خواهش میکنم دوست عزیز
سلام عالی بود انشا … کاربران بهره کافی رو ببرند
با سلام
ممنون وما هم امیدواریم دانش آموزان بهره لازم روببرند
سلام. ممنون میشم در الگوی
سلام من یک سوالی دادن گفتن که الگوی اعداد زیر را به صورت عبارت جبری بنویسید یعنی چی ؟
یعنی جمله عمومی یا همون معادله اش رو بنویس
دوست عزیز میتونید با خوندن این پست به جوابتون برسیدhttps://riazica.com/pattern-and-sequence/
باسلام میشه الگوی این اعداد رو پیدا کنید؟
5/2 ,15/2 5 , 10 , …
خیلی خوب بود استفاده کردم ممنون از زحمات شما
خییییییییییییییییییییییییییلی خوب وروان توضیح دادید
خئییییییییلی عالی واقعا پسندیدم
خدا قوت عالی
عالی هستید یک یک