مشتق توابع مثلثاتی 🔮📐 – تمام آنچه می‌خواهید!!

در درسنامهٔ مشتق توابع مثلثاتی به بررسی مشتق توابع سینوس، کسینوس و تانژانت می‌پردازیم. با یادگیری مشتق این توایع می‌توانیم مشتق بسیاری از توابع دیگر که شامل این توابع نیز هستند را به دست آوریم. سعی می‌کنیم با حل مثال‌های مختلف به درک بهتر شما از این مبحث کمک کنیم. با ما تا انتها همراه باشید.

مشتق سینوس

در قسمت اول از این درسنامه، مشتق تابع \(\Large f(x)=sin(x)\) را بررسی می‌کنیم. پیشنهاد می‌کنیم در صورتی که نیاز به مرور توابع مثلثاتی دارید، درسنامه‌ٔ نسبت‌های مثلثاتی را مرور کنید. برای مرور مبحث مشتق نیز می‌توانید درسنامهٔ مشتق دوازدهم را مطالعه کنید.

برای به دست آوردن مشتق تابع \(\Large f(x)=sin(x)\) از تعریف مشتق استفاده می‌کنیم. همان طور که به خاطر دارید، مشتق تابع \(\Large f(x)\) را به صورت زیر تعریف می‌کردیم:

\(\LARGE f'(x)=\lim\limits_{h \to 0}\frac{f(x+h)-f(x)}{h}\)

پس اگر تابع \(\Large f(x)=sin(x)\) را در رابطهٔ بالا قرار دهیم، داریم:

\(\LARGE f'(x)=\lim\limits_{h \to 0}\frac{sin(x+h)-sin(x)}{h}\)

\(\Large sin(x+h)\) را می‌توانیم با استفاده از رابطه‌ای که برای سینوس مجموع دو زاویه داشتیم، به صورت زیر بنویسیم:

\(\LARGE sin(x)cos(h)+cos(x)sin(h)\)

پس عبارت بالا را به جای \(\Large sin(x+h)\) در \(\Large f'(x)\) قرار می‌دهیم:

\(\Large f'(x)=\lim\limits_{h \to 0}\frac{sin(x)cos(h)+cos(x)sin(h)-sin(x)}{h}\)

اگر از جملهٔ اول و آخر صورت کسر بالا، \(\Large sin(x)\) را فاکتور بگیریم، به عبارت زیر می‌رسیم:

\(\Large f'(x)=\lim\limits_{h \to 0}\frac{sin(x)(cos(h)-1)+cos(x)sin(h)}{h}\)

کسر بالا را می‌توانیم به صورت مجموع دو کسر بنویسیم:

\(f'(x)=\lim\limits_{h \to 0}\frac{sin(x)(cos(h)-1)}{h}+\lim\limits_{h \to 0}\frac{cos(x)sin(h)}{h}\)

\(\Large sin(x)\) و \(\Large cos(x)\) در عبارت بالا نسبت به \(\Large h\) تغییر نمی‌کنند. کافی است \(\Large \lim\limits_{h \to 0}\frac{cos(h)-1}{h}\) و \(\Large \lim\limits_{h \to 0}\frac{sin(h)}{h}\) را محاسبه کرده و به ترتیب در \(\Large sin(x)\) و \(\Large cos(x)\) ضرب کنیم. می‌توان ثابت کرد \(\Large \lim\limits_{h \to 0}\frac{cos(h)-1}{h}=0\) و \(\Large \lim\limits_{h \to 0}\frac{sin(h)}{h}=1\) است. بنابراین داریم:

\(f'(x)=sin(x).\lim\limits_{h \to 0}\frac{(cos(h)-1)}{h}+cos(x).\lim\limits_{h \to 0}\frac{sin(h)}{h}\)

\(\LARGE =sin(x) \times 0 + cos(x) \times 1\)

\(\LARGE =cos(x)\)

بنابراین داریم:

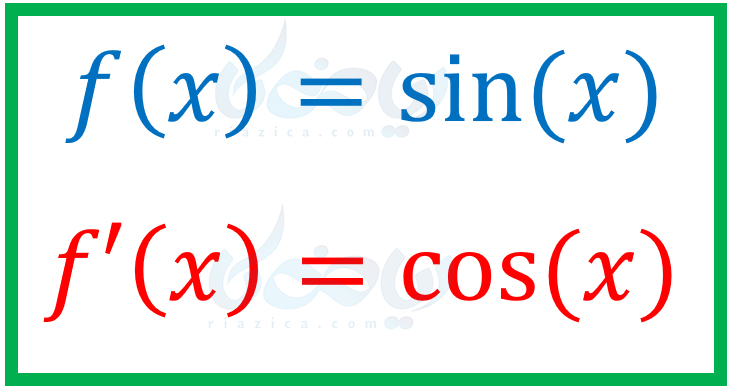
مثال از مشتق توابع مثلثاتی

مثال 1: مشتق تابع \(\Large f(x)=\frac{sin(x)}{sin(x)+1}\) را به دست آورید.

حل: همان طور که به خاطر دارید، اگر \(\Large f=\frac{g}{h}\) باشد، \(\Large f’=\frac{g’h-h’g}{h^2}\) خواهد بود. اگر بخواهیم تابع داده شده در صورت مسئله را به صورت \(\Large f=\frac{g}{h}\) بنویسیم، \(\Large g=sin(x)\) و \(\Large h=sin(x)+1\) خواهد بود. از طرفی داریم:

\(\LARGE g’=cos(x)\)

مشتق \(\Large h(x)=sin(x)+1\) نیز برابر است با حاصل جمع مشتق \(\Large sin(x)\) و \(\Large 1\). مشتق \(\Large 1\) که برابر با صفر است؛ بنابراین:

\(\LARGE h'(x)=cos(x)+0=cos(x)\)

در نتیجه، مشتق \(\Large f\) به صورت زیر است:

\(\LARGE f’=\frac{cos(x).(sin(x)+1)-cos(x).sin(x)}{(sin(x)+1)^2}\)

عبارت بالا را می‌توان ساده کرد؛ دو عبارت \(\LARGE cos(x).sin(x)\) و \(\LARGE -cos(x).sin(x)\) داریم که با یکدیگر ساده شده و \(\LARGE f’\) به صورت زیر در می‌آید:

\(\LARGE f’=\frac{cos(x)}{(sin(x)+1)^2}\)

مشتق کسینوس

برای به دست آوردن مشتق تابع \(\Large f(x)=cos(x)\) نیز می‌توانیم مشابه با تابع \(\Large f(x)=sin(x)\) عمل کنیم؛ یعنی اگر \(\Large f(x)=cos(x)\) باشد، داریم:

\(\LARGE f'(x)=\lim\limits_{h \to 0}\frac{cos(x+h)-cos(x)}{h}\)

\(\Large cos(x+h)\) را می‌توان با استفاده از رابطه‌ای که برای کسینوس مجموع دو زاویه داشتیم، به صورت زیر بنویسیم:

\(\LARGE cos(x)cos(h)-sin(x)sin(h)\)

عبارت بالا را به جای \(\Large cos(x+h)\) در \(\Large f'(x)\) قرار می‌دهیم:

\(\Large f'(x)=\lim\limits_{h \to 0}\frac{cos(x)cos(h)-sin(x)sin(h)-cos(x)}{h}\)

اگر از جملهٔ اول و آخر صورت کسر بالا، \(\Large cos(x)\) را فاکتور بگیریم، به عبارت زیر می‌رسیم:

\(\Large f'(x)=\lim\limits_{h \to 0}\frac{cos(x)(cos(h)-1)-sin(x)sin(h)}{h}\)

کسر بالا را می‌توانیم به صورت تفاضل دو کسر بنویسیم:

\(f'(x)=\lim\limits_{h \to 0}\frac{cos(x)(cos(h)-1)}{h}-\lim\limits_{h \to 0}\frac{sin(x)sin(h)}{h}\)

\(\Large sin(x)\) و \(\Large cos(x)\) در عبارت بالا نسبت به \(\Large h\) تغییر نمی‌کنند. بنابراین کافی است \(\Large \lim\limits_{h \to 0}\frac{cos(h)-1}{h}\) و \(\Large \lim\limits_{h \to 0}\frac{sin(h)}{h}\) را محاسبه کرده و به ترتیب در \(\Large cos(x)\) و \(\Large sin(x)\) ضرب کنیم. همان طور که در قسمت قبل نیز گفتیم، می‌توان ثابت کرد \(\Large \lim\limits_{h \to 0}\frac{cos(h)-1}{h}=0\) و \(\Large \lim\limits_{h \to 0}\frac{sin(h)}{h}=1\) است. بنابراین داریم:

\(f'(x)=sin(x).\lim\limits_{h \to 0}\frac{(cos(h)-1)}{h}+cos(x).\lim\limits_{h \to 0}\frac{sin(h)}{h}\)

\(\LARGE =cos(x) \times 0 – sin(x) \times 1\)

\(\LARGE =-sin(x)\)

بنابراین داریم:

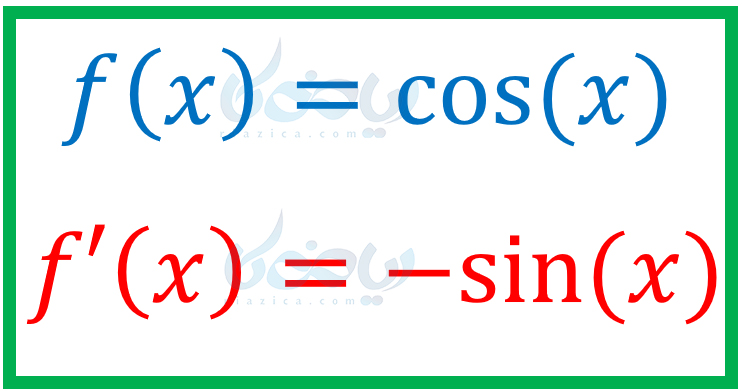
مثال از مشتق توابع مثلثاتی

مثال 2: مشتق تابع \(\Large f(x)=cos(x^2+3x)\) را به دست آورید.

حل: همان طور که به خاطر دارید، اگر \(\Large f(x)=g(h(x))\) باشد، \(\Large f’=g'(h(x)).h'(x)\) است. اگر بخواهیم تابع داده شده در صورت مسئله را به صورت \(\Large f(x)=g(h(x))\) بنویسیم، \(\Large g(x)=cos(x)\) و \(\Large h(x)=x^2+3x\) خواهد بود. از طرفی داریم:

\(\LARGE g'(x)=-sin(x)\)

\(\LARGE \Rightarrow g'(h(x))=-sin(x^2+3x)\)

همچنین داریم:

\(\LARGE h'(x)=2x+3\)

پس، مشتق \(\LARGE f\) به صورت زیر به دست می‌آید:

\(\Large f'(x)=(-sin(x^2+3x)).(2x+3)\)

مشتق تانژانت

برای محاسبهٔ مشتق تابع \(\Large f(x)=tan(x)\) کافی است از تعریف تابع تانژانت و مشتق توابع کسری استفاده کنیم. طبق تعریف تابع تانژانت داریم:

\(\LARGE f(x)=tan(x)=\frac{sin (x)}{cos (x)}\)

از طرفی می‌دانیم، مشتق یک تابع کسری مانند \(\Large f=\frac{g}{h}\) برابر است با:

\(\LARGE f’=\frac{g’h-h’g}{h^2}\)

بنابراین، مشتق تابع \(\LARGE tan(x)=\frac{sin (x)}{cos (x)}\) به صورت زیر است:

\(\LARGE f'(x)=\frac{cos(x).cos(x)-(-sin(x)).sin(x)}{cos^2 (x)}\)

\(\LARGE =\frac{cos^2(x)+sin^2(x)}{cos^2 (x)}\)

از طرفی می‌دانیم صورت کسر بالا برابر با 1 است. بنابراین:

\(\LARGE f'(x)=\frac{1}{cos^2 (x)}\)

پس داریم:

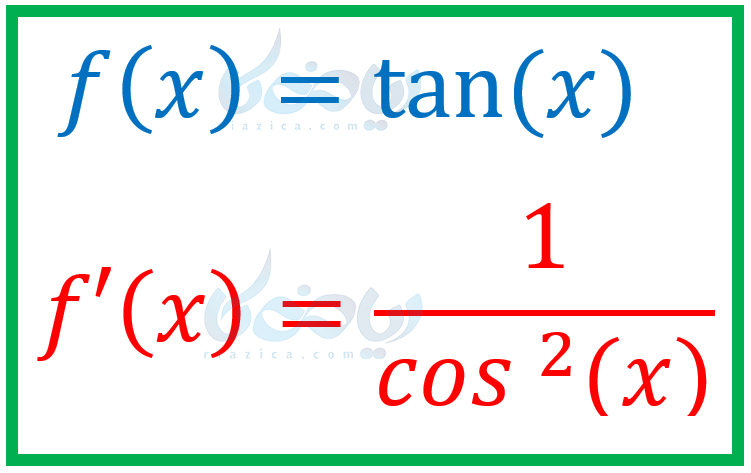
مثال از مشتق توابع مثلثاتی

مثال 3: مشتق تابع \(\Large f(x)=tan^2(x)\) را به دست آورید.

حل: می‌دانیم اگر \(\Large f(x)=g^2(x)\) باشد، \(\Large f'(x)=2g(x).g'(x)\) خواهد بود. در این مثال، \(\Large g(x)\) همان \(\Large tan(x)\) است. پس داریم:

\(\LARGE f'(x)=2tan(x).\frac{1}{cos^2(x)}\)

اگرچه نیاز نیست، ولی می‌توانیم عبارت بالا را ساده‌تر کنیم. کافی است در عبارت بالا به جای \(\Large tan(x)\) عبارت \(\Large \frac{sin(x)}{cos(x)}\) را قرار دهیم:

\(\LARGE f'(x)=2\frac{sin(x)}{cos(x)}.\frac{1}{cos^2(x)}\)

\(\LARGE \Rightarrow f'(x)=2\frac{sin(x)}{cos^3(x)}\)

مثال از مشتق توابع مثلثاتی

مثال 4: مشتق تابع \(\Large f(x)=tan(cos(x))cos(cos(x))\) را به دست آورید.

حل: همیشه قبل از محاسبهٔ مشتق یک تابع، تا جای ممکن آن را ساده کنید. در عبارت بالا اگر به جای \(\Large tan(cos(x))\) بنویسیم \(\Large \frac{sin(cos(x))}{cos(cos(x))}\)، آنگاه \(\Large f(x)\) به صورت زیر در خواهد آمد:

\(\LARGE f(x)=\frac{sin(cos(x))}{cos(cos(x))}cos(cos(x))\)

همان طور که در عبارت بالا می‌بینید، می‌توانیم \(\Large cos(cos(x))\) را ساده کنیم و به عبارت زیر برسیم:

\(\LARGE f(x)=sin(cos(x))\)

حال از رابطه‌ای که برای مشتق ترکیب توابع داشتیم استفاده می‌کنیم؛ همان طور که به خاطر دارید، اگر \(\Large f(x)=g(h(x))\) باشد، آنگاه \(\Large f'(x)=g'(h(x))h'(x)\) است. در اینجا \(\Large g(x)=sin(x)\) و \(\Large h(x)=cos(x)\) است. بنابراین داریم:

\(\LARGE f'(x)=cos(cos(x)).(-sin(x))\)

زنگ آخر درسنامهٔ مشتق توابع مثلثاتی

در درسنامه‌ای که از حسابان 2 خواندیم، مشتق توابع سینوس، کسینوس و تانژانت را بررسی کرده و به حل مثال از آن‌ها پرداختیم.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با درسنامهٔ مشتق توابع مثلثاتی دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.