آموزش ریاضی پایه نهم
جمع و تفریق رادیکال ها ⚡️➕ – مثل جملات متشابه رفتار کن!
در درسنامۀ جمع و تفریق رادیکال ها روش ساده سازی عبارتهای شامل رادیکال را خواهیم آموخت. ابتدا روش جمع و تفریق عبارتهای رادیکالی را بررسی میکنیم. سپس به بررسی روش ساده سازی عبارت های رادیکالی میپردازیم. در انتها نیز، چگونگی گویا کردن مخرج کسرهایی که رادیکالی هستند را با یکدیگر میبینیم. سعی کردیم با حل مثالهای مختلف، در درک بهتر مبحث جمع و تفریق رادیکال ها به شما کمک کنیم. با ما تا انتها همراه باشید.
جمع و تفریق قسمت رادیکالی
همان طور که برای عبارتهای جبری، جملات متشابه تعریف میکردیم، برای رادیکال ها نیز میتوانیم جملات متشابه (یکسان) تعریف کنیم. دو رادیکال متشابهاند اگر عدد زیر دو رادیکال و فرجۀ دو رادیکال با هم برابر باشند. در صورتی که دو رادیکالِ متشابه (یکسان) داشته باشیم، میتوانیم ضرایب آن دو را با هم جمع و یا از یکدیگر تفریق کنیم. مثلاً دو رادیکال \(\Large 2\sqrt{3}\) و \(\Large 4 \sqrt{3}\) متشابه هستند. زیرا در هر دو، عدد زیر رادیکال برابر است با \(\Large 3\). همچنین فرجۀ رادیکال در هر دو برابر با \(\Large 2\) است. بنابراین حاصل جمع ضرایب این دو رادیکال به صورت زیر خواهد شد:
\(\LARGE 2\sqrt{3}+4 \sqrt{3}=6 \sqrt{3}\)
دقت کنید، به هیچ عنوان عدد زیر دو رادیکال متشابه را جمع و تفریق نمیکنیم. جمع و تفریق تنها بر روی ضرایب دو رادیکال متشابه صورت میگیرد. یا مثلاً اگر بخواهیم عبارت \(\Large 2\sqrt{3}\) را از \(\Large 4 \sqrt{3}\) کم کنیم، ضرایب دو رادیکال را به صورت زیر تفریق میکنیم:
\(\LARGE 4 \sqrt{3}- 2 \sqrt{3}=2 \sqrt{3}\)
اما اگر دو عبارت \(\Large 2\sqrt{5}\) و \(\Large 3 \sqrt{2}\) را داشته باشیم، دیگر نمیتوانیم آنها را با یکدیگر جمع و یا از یکدیگر کم کنیم. زیرا قسمت رادیکالی این دو عبارت متفاوت هستند. یا به طور مثال، قسمتهای رادیکالی دو عبارت \(\Large \sqrt[3]{5}\) و \(\Large 2\sqrt{5}\) متفاوت است و نمیتوان این دو عبارت را با یکدیگر جمع و یا از یکدیگر تفریق نمود. به مثال بعدی از درسنامۀ جمع و تفریق رادیکال ها توجه کنید.
مثال از جمع و تفریق رادیکال ها
مثال 1: در جدول زیر سه ستون وجود دارد. مجموع هر ستون را بیابید.
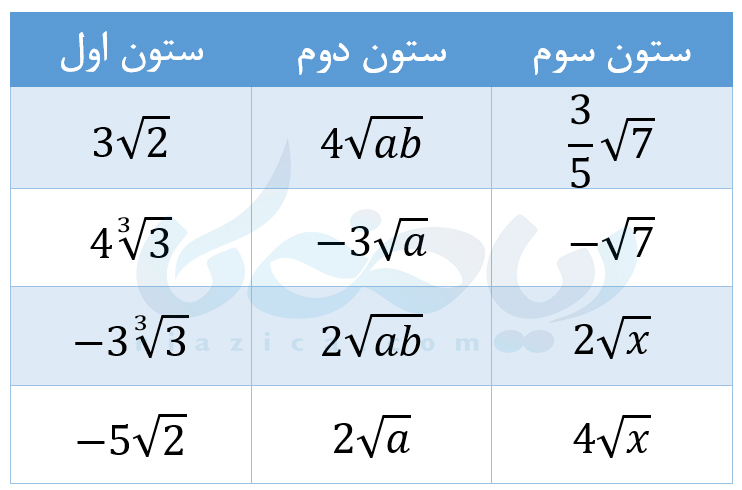
حل: در این مثال از درسنامۀ جمع و تفریق رادیکال ها هر ستون را به تفکیک بررسی میکنیم:
- ستون اول: عبارتهای \(\Large 3 \sqrt{2}\) و \(\Large -5 \sqrt{2}\) دارای قسمتهای رادیکالی یکسان هستند و مجموعشان برابر است با \(\Large -2 \sqrt{2}\). همچنین، عبارتهای \(\Large 4 \sqrt[3]{3}\) و \(\Large -3 \sqrt[3]{3}\) دارای قسمت رادیکالی یکسان هستند و مجموعشان برابر است با \(\Large \sqrt[3]{3}\). بنابراین مجموع عبارات ستون اول برابر است با \(\Large -2 \sqrt{2}+\sqrt[3]{3}\).
- ستون دوم: عبارتهای \(\Large 4 \sqrt{ab}\) و \(\Large 2 \sqrt{ab}\) دارای قسمتهای رادیکالی یکسان هستند و مجموعشان برابر است با \(\Large 6 \sqrt{ab}\). همچنین، عبارتهای \(\Large -3 \sqrt{a}\) و \(\Large 2 \sqrt{a}\) دارای قسمت رادیکالی یکسان هستند و مجموعشان برابر است با \(\Large – \sqrt{a}\). بنابراین مجموع عبارات ستون دوم برابر است با \(\Large 6 \sqrt{ab}- \sqrt{a}\).
- ستون سوم: عبارتهای \(\Large \frac{3}{5} \sqrt{7}\) و \(\Large -\sqrt{7}\) دارای قسمتهای رادیکالی یکسان هستند و مجموعشان برابر است با \(\Large – \frac{2}{5}\sqrt{7}\). همچنین، عبارتهای \(\Large 2 \sqrt{x}\) و \(\Large 4 \sqrt{x}\) دارای قسمت رادیکالی یکسان هستند و مجموعشان برابر است با \(\Large 6 \sqrt{x}\). بنابراین مجموع عبارات ستون سوم برابر است با \(\Large – \frac{2}{5}\sqrt{7}+ 6 \sqrt{x}\).
در جدول زیر، مجموع هر ستون، زیر آن نوشته شده است:
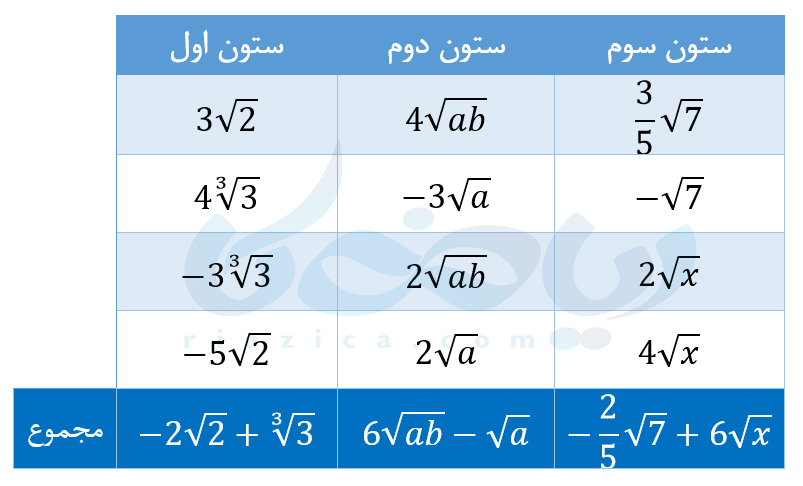
به قسمت بعدی از درسنامۀ جمع و تفریق رادیکال ها توجه کنید.
ساده کردن عبارت های رادیکالی
برای ساده کردن عبارتهای رادیکالی، ایتدا باید اعداد زیر رادیکال را ساده کنیم. منظورمان از ساده کردن چیست؟ مثلاً فرض کنید یک عدد زیر رادیکال داریم و فرجۀ رادیکال برابر با \(\Large 2\) است. در این صورت باید ببینیم که آیا میتوان عدد داده شده را به صورت حاصل ضرب یک مربع کامل در عددی دیگر نوشت یا خیر. اگر میتوانیم این کار را بکنیم، عدد را به صورت حاصل ضرب یک مربع کامل در عددی دیگر مینویسیم تا بتوانیم مربع کامل را از زیر رادیکال خارج کنیم. برای فرجههای دیگر نیز به تناسب همین کار را میکنیم. مثلاً برای فرجۀ سه (ریشۀ سوم)، باید به دنبال مکعب کامل باشیم. به طور کلی میتوانیم عدد را تجزیه کنیم تا مربع کامل یا مکعب کامل (یا موارد دیگر) را پیدا کنیم. البته گاهی هم ممکن است با اعدادی زیر رادیکال سر و کار داشته باشیم که قابل ساده شدن نباشند. مثلاً \(\Large \sqrt{30}\) ساده نمیشود زیرا عدد \(\Large 30\) را نمیتوان به صورت حاصل ضرب یک مربع کامل در عددی دیگر نوشت. برای اینکه بهتر متوجه شوید، به مثالهای بعدی از درسنامۀ جمع و تفریق رادیکال ها توجه کنید.
ساده کردن جمع و تفریق رادیکال ها
مثال 2: عبارت \(\Large \sqrt{12}-\sqrt{48}+\sqrt{27}\) را ساده کنید.
حل: \(\Large \sqrt{12}\) را میتوانیم به صورت \(\Large \sqrt{4 \times 3}\) بنویسیم. همان طور که در بالا توضیح دادیم، دلیل این کار این است که \(\Large 4\) مربع کامل است و میتوان آن را از زیر رادیکال خارج کرد. همان طور که در درسنامۀ ریشه گیری ریاضی نهم گفتیم، ریشۀ دومِ حاصل ضربِ دو عدد مثبت برابر است با حاصل ضرب ریشۀ دومِ هر یک از آنها. بنابراین داریم:
\(\LARGE \sqrt{12}=\sqrt{4 \times 3}\)
\(\LARGE =\sqrt{4} \times \sqrt{3}\)
\(\LARGE =2 \times \sqrt{3}\)
به همین ترتیب، \(\Large \sqrt{48}\) به صورت زیر ساده میشود:
\(\LARGE \sqrt{48}=\sqrt{16 \times 3}\)
\(\LARGE =\sqrt{16} \times \sqrt{3}\)
\(\LARGE =4 \times \sqrt{3}\)
عبارت \(\Large \sqrt{27}\) نیز در این مثال از درسنامۀ جمع و تفریق رادیکال ها به صورت زیر در میآید:
\(\LARGE \sqrt{27}=\sqrt{9 \times 3}\)
\(\LARGE =\sqrt{9} \times \sqrt{3}\)
\(\LARGE =3 \times \sqrt{3}\)
بنابراین، عبارت \(\Large \sqrt{12}-\sqrt{48}+\sqrt{27}\) برابر است با:
\(\LARGE 2 \times \sqrt{3}-4 \times \sqrt{3}+3 \times \sqrt{3}\)
حال از نکتهای که در این درسنامه در مورد جمع و تفریق رادیکال ها گفتیم، استفاده میکنیم. از آنجاییکه قسمت رادیکالی هر سه عبارت یکسان است، میتوانیم آنها را با یکدیگر جمع و یا از یکدیگر کم کنیم. بنابراین پاسخ نهایی مسئله برابر است با \(\Large \sqrt{3}\). به مثال بعدی از درسنامۀ جمع و تفریق رادیکال ها توجه کنید.
ساده کردن عبارات شامل ریشۀ سوم
مثال 3: عبارت \(\Large \sqrt[3]{250}-2\sqrt[3]{128}+\sqrt[3]{54}\) را ساده کنید.
حل: دقیقاً تمام مراحلی را که برای حل مثال 2 طی کردیم، میتوانیم برای حل این مثال نیز طی کنیم. \(\Large \sqrt[3]{250}\) را میتوانیم به صورت \(\Large \sqrt[3]{125 \times 2}\) بنویسیم. از طرفی همان طور که در درسنامۀ ریشه گیری ریاضی نهم گفتیم، ریشۀ سومِ حاصل ضربِ دو عدد برابر است با حاصل ضرب ریشۀ سومِ هر یک از آنها. بنابراین داریم:
\(\LARGE \sqrt[3]{250}=\sqrt[3]{125 \times 2}\)
\(\LARGE =\sqrt[3]{125} \times \sqrt[3]{2}\)
\(\LARGE =5 \times \sqrt[3]{2}\)
به همین ترتیب، \(\Large 2\sqrt[3]{128}\) به صورت زیر ساده میشود:
\(\LARGE 2\sqrt[3]{128}=2\sqrt[3]{64 \times 2}\)
\(\LARGE =2\times \sqrt[3]{64} \times \sqrt[3]{2}\)
\(\LARGE =2 \times 4 \times \sqrt[3]{2}\)
\(\LARGE =8 \sqrt[3]{2}\)
عبارت \(\Large \sqrt[3]{54}\) نیز در این مثال از درسنامۀ جمع و تفریق رادیکال ها به صورت زیر در میآید:
\(\LARGE \sqrt[3]{54}=\sqrt[3]{27 \times 2}\)
\(\LARGE =\sqrt[3]{27} \times \sqrt[3]{2}\)
\(\LARGE =3 \times \sqrt[3]{2}\)
بنابراین، عبارت \(\Large \sqrt[3]{250}-2\sqrt[3]{128}+\sqrt[3]{54}\) برابر است با:
\(\LARGE 5 \times \sqrt[3]{2}-8 \sqrt[3]{2}+3 \times \sqrt[3]{2}\)
حال از نکتهای که در این درسنامه در مورد جمع و تفریق رادیکال ها گفتیم، استفاده میکنیم. از آنجاییکه قسمت رادیکالی هر سه عبارت یکسان است، میتوانیم آنها را با یکدیگر جمع و یا از یکدیگر کم کنیم. بنابراین پاسخ نهایی مسئله برابر است با \(\Large 0\). به مثال بعدی از درسنامۀ جمع و تفریق رادیکال ها توجه کنید.
ساده کردن ضرب دو عبارت رادیکالی
مثال 4: عبارت \(\Large (\sqrt{5}-2\sqrt{2})(\sqrt{2}+3\sqrt{5})\) را ساده کنید.
حل: باید از خاصیت پخشی استفاده کنیم. یعنی هر یک از عبارات داخل پرانتز اول را در تک تک عبارات داخل پرانتز دوم ضرب کنیم. بر این اساس داریم:
\(\LARGE (\sqrt{5}-2\sqrt{2})(\sqrt{2}+3\sqrt{5})\)
\(\LARGE =\sqrt{5} \times \sqrt{2}+\sqrt{5} \times 3\sqrt{5}\)
\(\LARGE -2\sqrt{2} \times \sqrt{2}-2\sqrt{2} \times 3\sqrt{5}\)
حاصل ضرب ریشۀ دوم دو عدد مثبت برابر است با ریشۀ دوم حاصل ضرب آنها. بنابراین عبارت بالا برابر است با:
\(\LARGE \sqrt{10}+3\sqrt{25} -2\sqrt{4}-6\sqrt{10} \)
\(\LARGE =\sqrt{10}+15 -4-6\sqrt{10} \)
\(\LARGE =\sqrt{10}+11-6\sqrt{10} \)
قسمت رادیکالی دو عبارت \(\Large \sqrt{10}\) و \(\Large -6\sqrt{10}\) یکسان است. بنابراین این دو عبارت را با هم جمع میکنیم تا پاسخ نهایی مسئله به صورت زیر درآید:
\(\LARGE =-5\sqrt{10}+11 \)
به قسمت بعدی از درسنامۀ جمع و تفریق رادیکال ها توجه کنید.
گویا کردن مخرج کسرها
گاهی با کسرهایی رو به رو هستیم که دارای مخرج رادیکالی هستند و برای ما مطلوب است تا مخرجشان را گویا کنیم.منظورمان از گویا کردن این است که مخرج را از حالت رادیکالی خارج کیم. به این منظور باید، صورت و مخرج کسر را در رادیکالی متناسب با رادیکال مخرج ضرب کنیم، تا مخرج از حالت رادیکالی خارج شده و به عدد گویا تبدیل شود. دقت کنید، چون صورت و مخرج کسر را در یک عدد یکسان ضرب کردهایم، مانند این است که کل کسر در عدد \(\Large 1\) ضرب شده است. بنابراین مقدار کسر تغییری نمیکند. مثلاً فرض کنید که میخواهیم مخرج کسر \(\Large \frac{1}{\sqrt{2}}\) را گویا کنیم. کافی است صورت و مخرج آن را در \(\Large \sqrt{2}\) ضرب کنیم:
\(\LARGE \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}= \frac{1 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}}\)
\(\LARGE = \frac{\sqrt{2}}{\sqrt{2 \times2}}= \frac{\sqrt{2}}{2}\)
برای درک بهتر این قسمت از درس، میتوانید به درسنامۀ گویا کردن مخرج گنگ نیز مراجعه کنید. به مثالهای بعدی از درسنامۀ جمع و تفریق رادیکال ها توجه کنید.
مثال از گویا کردن مخرج کسر
مثال 5: مخرج کسر \(\Large \frac{2}{\sqrt{\frac{3}{5}}}\) را گویا کنید.
حل: ریشۀ دوم حاصل تقسیم دو عدد (با مخرج غیر صفر) برابر است با حاصل تقسیم ریشۀ دوم دو عدد. بنابراین داریم:
\(\LARGE \frac{2}{\sqrt{\frac{3}{5}}}=\frac{2}{\frac{\sqrt{3}}{\sqrt{5}}}=\frac{2\sqrt{5}}{\sqrt{3}}\)
حال کافی است صورت و مخرج کسر بالا را در \(\Large \sqrt{3}\) ضرب کنیم تا عدد \(\Large 3\) زیر رادیکال، مربع کامل شده و از زیر رادیکال خارج شود:
\(\LARGE \frac{2\sqrt{5}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}=\frac{2\sqrt{5}\times \sqrt{3}}{\sqrt{3}\times \sqrt{3}}\)
\(\LARGE =\frac{2\sqrt{15}}{\sqrt{9}}=\frac{2\sqrt{15}}{3}\)
به مثال بعدی از درسنامۀ جمع و تفریق رادیکال ها توجه کنید.
گویا کردن مخرجِ دارای ریشۀ سوم
مثال 6: مخرج کسر \(\Large \frac{3}{\sqrt[3]{2}}\) را گویا کنید.
حل: باید کاری کنیم که عدد \(\Large 3\) زیر رادیکال مکعب کامل شده تا از زیر رادیکال خارج شود. بنابراین صورت و مخرج کسر داده شده را در \(\Large \sqrt[3]{2^2}\) ضرب میکنیم:
\(\LARGE \frac{3}{\sqrt[3]{2}} \times \frac{\sqrt[3]{2^2}}{\sqrt[3]{2^2}}=\frac{3\times \sqrt[3]{2^2}}{\sqrt[3]{2}\times \sqrt[3]{2^2}}\)
\(\LARGE =\frac{3\sqrt[3]{4}}{\sqrt[3]{2\times 2^2}}=\frac{3\sqrt[3]{4}}{\sqrt[3]{2^3}}=\frac{3\sqrt[3]{4}}{2} \)
به مثال بعدی از درسنامۀ جمع و تفریق رادیکال ها توجه کنید.
گویا کردن مخرجِ دارای متغیر
مثال 7: مخرج کسر \(\Large \frac{2}{\sqrt[3]{x^2}}\) را گویا کنید.
حل: با متغیر و عبارتهای جبری در درسنامۀ عبارت های جبری هفتم آشنا شدهاید. همان طور که میدانید با متغیرها میتوان مانند اعداد رفتار کرد. بنابراین برای گویا کردن مخرج کسر این مثال نیز، درست مانند مثال 6 عمل میکنیم. یعنی باید صورت و مخرج کسر داده شده را در عبارتی ضرب کنیم که به واسطۀ آن، عبارت \(\Large x^2\) در مخرج کسر مکعب کامل شده و از زیر رادیکال خارج شود. منظور از مکعب کامل، توان سه و یا هر توانی است که بر سه بخش پذیر باشد، مثل شش، نه و غیره. بنابراین، صورت و مخرج کسر را در عبارت \(\Large \sqrt[3]{x}\) ضرب میکنیم:
\(\LARGE \frac{2}{\sqrt[3]{x^2}} \times \frac{\sqrt[3]{x}}{\sqrt[3]{x}}=\frac{2 \times \sqrt[3]{x}}{\sqrt[3]{x^2} \times \sqrt[3]{x}} \)
\(\LARGE =\frac{2 \sqrt[3]{x}}{\sqrt[3]{x^2 \times x}}=\frac{2 \sqrt[3]{x}}{\sqrt[3]{x^3}}=\frac{2 \sqrt[3]{x}}{x} \)
ویدیو از جمع وتفریق رادیکال ها
در این ویدیو با مثال های متعدد ساده کردن رادیکال ها وجمع وتفریق رادیکال ها وضرب آنها بیان شده
زنگ آخر کلاس جمع و تفریق رادیکال ها
در این درسنامه از ریاضی نهم دیدیم که در صورتی که قسمت رادیکالی دو عبارت، یکسان باشند، میتوانیم آن دو عبارت را با هم جمع و یا از یکدیگر کم کنیم. با دانستن این موضوع و همچنین استفاده از دانستههایمان در درسنامۀ ریشه گیری ریاضی نهم، عبارات رادیکالی را ساده کردیم. در انتهای درسنامه نیز، روش گویا کردن مخرج رادیکالی کسرها را بررسی کردیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با این مبحث دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





هفتم ?? – اعداد اولشو بشمار!
عالی
با سلام واحترام
ممنون از لطف شما
سلام جمع دو عدد که جذر کامل هستن زیر رادیکال رو چطور باید حل کنیم؟
مثلا ۱۰۰+۸۱
با سلام واحترام
حتما باید اول جمع کنید بعد جذر بگیرید
دمت گرم.یه خسته نباشید جانانه..
واقعا کیف کردم مطالب کامل و جامع.
با سلام و وقت به خیر
ما هم بادیدن این نظرات شارژ میشیم برای ادامه کار
سلام .ممنون از زحماتتون .مفید وکمک کننده
با سلام واحترام
خدا رو شکر وسپاس از شما
استاد عزیز خیلی ممنونم از زحماتتون
اگر سه عدد طبیعی رادیکالی رو بخوای جمع و تفریق کنیم چطوری میشه؟؟
پیشاپیش سپاسگزارم
با سلام وادب
اگه عدد زیر رادیکال وفرجه ها یکی باشه مثل عبارتهای جبری ضرایبشون رو جمع وتفریق میکنیم وگرنه ساده نمیشن
رادیکال و کسر ۲۵ به روی ۶۴ رو چجوری حل میکنن؟
خب اگه فرجه رادیکال ها مثل هم بود مثلا 2بود
هردو رو زیر یک رادیکال میبریم و بعدش حلش میکنیم یا جدا جدا اینجوری که رادیکال 25 با فرجه دو میشه 5 و رادیکال 64با فرجه2برابر 8:)
با سلام و احترام
بسیار سپاسگزارم از مطالب فوق العاده و کاملتون 🌹
ان شاءالله همواره پایدار و سلامت باشید 🙏
با سلام وادب
ممنون از نگاه شما
ممنونم
برای جمع اعدا رادیکالی رادیکال ۱ تا رادیکال ۷۵ به چند جمع نیاز داریم؟
با سلام … آموزنده و مفید بود سلامت و تندرست باشید
سلام ببخشید عبارت چهار منهای دو رادیکال سه که زیر رادیکال باشه رو چطور باید حساب کنیم؟
با سلام دوست عزیز
این عبارتی که شما میگید بیشتر از این ساده نمیشه
سلام
اگه سوال بده که رادیکال منفی هشت با فرجه هشت باشه جواب برابر چند میشه
سلام دوست عزیز اعداد منفی ریشه زوج ندارن پس این رادیکال بی معنی وتعریف نشده هست