آموزش ریاضی پایه نهم
معادله خط ریاضی نهم 📈✏️ – خط شو رسم کن!
در درسنامۀ معادله خط ریاضی نهم قصد داریم تا با معادلۀ خط به صورت کلی آشنا شویم. به این منظور، ابتدا رابطۀ بین ضلع و محیط مربع را به عنوان دو متغیر به دست آورده و آن را در دستگاه مختصات نشان میدهیم. در ادامه، پاسخ معادلات دو متغیره را بررسی میکنیم. در انتها نیز، با معادلۀ خط رآشنا شده و خطوط گذرنده از مبدأ را بررسی میکنیم. سعی میکنیم با حل مثالهای مختلف، به درک بهتر شما از این مبحث کمک کنیم. به اولین قسمت از درسنامۀ معادله خط ریاضی نهم توجه کنید.
رابطه بین دو متغیر
در درسنامۀ الگوهای عددی ریاضی هفتم، با متغیر آشنا شدیم. به زبان ساده، متغیرها اشیای نامعلومی هستند که میتوانند نشان دهندۀ کمیتها و اندازههای مختلف باشند. گاهی بین دو متغیر، یک رابطه وجود دارد. مثلاً اگر طول ضلع یک مربع را با \(\Large x\) و محیط آن را با \(\Large y\) نشان دهیم، آن گاه میتوانیم بنویسیم:
\(\LARGE y=4x\)
اندازۀ ضلع مربع هر عددی باشد، اندازۀ محیط مربع چهار برابر آن است. پس، رابطۀ بالا همیشه برقرار است. میتوانیم به جای \(\Large x\)، اعداد مختلف را قرار داده و مقدار \(\Large y\) را به دست آوریم:
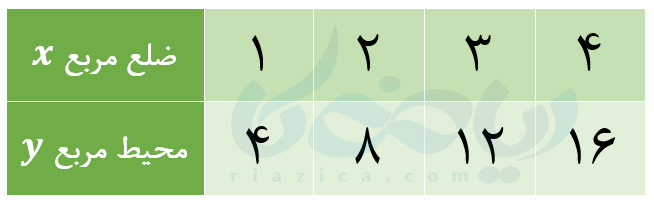
همچنین میتوانیم هر جفت عددی را که در جدول بالا به دست آوریم، به شکل \(\Large \begin{bmatrix} x \\ y \end{bmatrix}\) نمایش دهیم:
\(\LARGE \begin{bmatrix} 1 \\ 4 \end{bmatrix}\), \(\LARGE \begin{bmatrix} 2 \\ 8 \end{bmatrix}\), \(\LARGE \begin{bmatrix} 3 \\ 12 \end{bmatrix}\), \(\LARGE \begin{bmatrix}4 \\ 16 \end{bmatrix}\)
اگر هر یک از جفت عددهای بالا را به صورت یک نقطه در دستگاه مختصات نشان داده و آنها را به هم وصل کنیم، شکل زیر حاصل میشود:
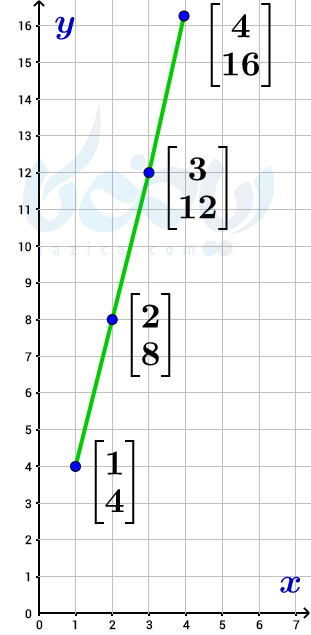
همان طور که در شکل بالا میبینید، نقاطی که به دست آوردیم، روی یک خط قرار دارند. لزوماً همیشه این اتفاق نمیافتد. مثلاً اگر رابطۀ بین مساحت یک مربع با ضلع آن را به دست میآوردیم، شکل حاصل از وصل کردن نقاط، خط نمیشد. در انتهای درسنامه خواهیم دید که در چه صورتی، رابطۀ بین دو متغیر به صورت خط در میآید. به قسمت بعدی از درسنامۀ معادله خط ریاضی نهم توجه کنید.
پاسخ معادلات دو متغیره
در درسنامۀ معادله ریاضی هفتم، با معادلاتی که تنها یک متغیر دارند آشنا شدیم. روش به دست آوردن پاسخ این معادلات را نیز دیدیم. اگر یک معادله با دو متغیر داشته باشیم، چه طور؟ چگونه میتوانیم آن را حل کنیم. فرض کنید معادلۀ \(\Large x+y=5\) را داریم و میخواهیم چهار جواب برای آن پیدا کنیم. برای حل چنین معادلهای، اگر به \(\Large x\) مقداردهی کنیم، معادلۀ دو متغیرۀ ما به معادلۀ یک متغیره تبدیل میشود. مثلاً اگر \(\Large x\) را برابر با \(\Large 1\) قرار دهیم، آنگاه معادلۀ \(\Large x+y=5\) تبدیل به معادلۀ زیر میشود:
\(\LARGE 1+y=5\)
بدیهی است، مقدار \(\Large y\) در معادلۀ بالا برابر با \(\Large 4\) است. به همین ترتیب میتوانیم \(\Large x\) را با سه مقدار دیگر جایگزین کرده و به ازای هر یک از آنها، مقدار \(\Large y\) را به دست آوریم. مثلاً اگر \(\Large x=0\) باشد، \(\Large y=5\) است، اگر \(\Large x=-1\) باشد، \(\Large y=6\) است و اگر \(\Large x=2.5\) باشد، \(\Large y=2.5\) است. چهار جفت جوابی را که برای \(\Large x\) و \(\Large y\) به دست آوردیم، میتوانیم به صورت زیر نمایش دهیم:
\(\LARGE \begin{bmatrix} 1 \\ 4 \end{bmatrix}\), \(\LARGE \begin{bmatrix} 0 \\ 5 \end{bmatrix}\), \(\LARGE \begin{bmatrix} -1 \\ 6 \end{bmatrix}\), \(\LARGE \begin{bmatrix}2.5 \\ 2.5 \end{bmatrix}\)
همچنین میتوانیم مانند قسمت قبل، هر یک از جوابهای بالا را به صورت یک نقطه در دستگاه مختصات نشان داده و آنها را به هم وصل کنیم:

هر یک از نقاطی که روی خط بالا قرار دارند، جواب معادله هستند. در واقع معادلۀ ما بی شمار جواب در مجموعۀ اعداد حقیقی دارد. در قسمت بعدی از درسنامۀ معادله خط ریاضی نهم خواهیم دید که در چه صورتی یک معادله، نشان دهندۀ یک خط در صفحه است.
معادلۀ خط
هر معادلهای به شکل \(\Large y=ax+b\) که در آن \(\Large a\) و \(\Large b\) اعداد حقیقی دلخواه و \(\Large x\) و \(\Large y\) متغیر هستند، معادلۀ یک خط در صفحه است. اگر مانند قسمتهای قبل، تمام نقاطی که در معادلۀ بالا صدق میکنند را در دستگاه مختصات رسم کنیم، شکل حاصل یک خط خواهد شد. اصطلاحاً در چنین حالتی میگوییم \(\Large x\) و \(\Large y\) بایکدیگر رابطۀ خطی دارند. در جدول زیر، سه معادلۀ خط نوشته و در آن \(\Large a\) و \(\Large b\) را مشخص کردهایم:
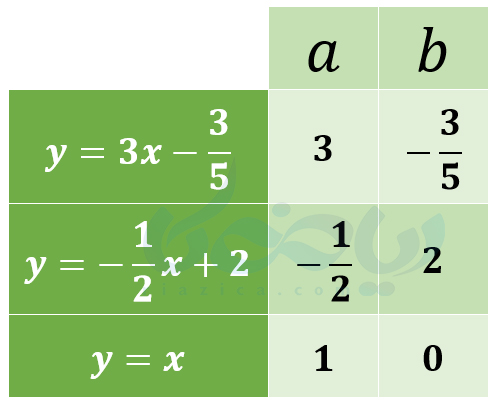
دو نکته را به صورت کوتاه ذکر میکنیم اما بررسی و حل مثال از آنها را به درسنامۀ شیب خط و عرض از مبدا ریاضی نهم موکول میکنیم:
- معادلاتی به شکل \(\Large x=a\) یا \(\Large y=a\) نیز معادلۀ خط هستند.
- صورت کلی معادلات خطی در صفحه، به صورت \(\Large ax+by=c\) است. یعنی در یک معادلۀ خط، لزومی ندارد ضریب \(\Large y\) برابر با \(\Large 1\) باشد.
از آنجاییکه هدف این درسنامه آشنایی ابتدایی با معادلۀ خط است، تنها خطوط به شکل کلی \(\Large y=ax+b\) را بررسی کرده و خطوطی که در دو نکتۀ قبل به آنها اشاره کردیم را در درسنامۀ بعدی بررسی میکنیم. به قسمت بعدی از درسنامۀ معادله خط ریاضی نهم توجه کنید.
رسم خط
برای رسم یک خط در حالت کلی، تنها داشتن دو نقطه از آن کافی است (البته برای علاقهمندان باید گفت که این جمله در هندسۀ اقلیدسی صحیح است. در صورتی که مایلید، در مورد هندسههای نااقلیدسی مطالعه کنید). بنابراین اگر معادلۀ خطی را داشته باشیم و بخواهیم آن را در دستگاه مختصات رسم کنیم، کافی است دو نقطه که در آن معادله صدق میکنند را پیدا کنیم. از وصل کردن آن دو نقطه به هم و امتداد آن، خطی که میخواستیم به دست میآید. برای اینکه بهتر متوجه شوید، به مثالهای بعدی از درسنامۀ معادله خط ریاضی نهم توجه کنید.
مثال از درسنامۀ معادله خط ریاضی نهم
مثال 1 معادله خط ریاضی نهم: خط به معادلۀ \(\Large y=x+2\) را رسم کنید.
حل: همان طور که گفتیم، کافی است دو نقطه پیدا کنیم که در معادلۀ بالا صدق کنند. منظور از دو نقطه، دو جفت \(\Large x\) و \(\Large y\) است. اگر \(\Large x\) را برابر با \(\Large 0\) قرار دهیم، مقدار \(\Large y\) برابر با \(\Large 2\) خواهد بود. در نتیجه، نقطۀ \(\Large \begin{bmatrix} 0\\ 2\end{bmatrix}\) در معادلۀ بالا صدق میکند. به همین ترتیب، اگر \(\Large x\) را برابر با \(\Large 1\) قرار دهیم، مقدار \(\Large y\) برابر با \(\Large 3\) خواهد بود. بنابراین، نقطۀ \(\Large \begin{bmatrix} 1\\ 3\end{bmatrix}\) نیز در معادلۀ بالا صدق میکند. حال کافی است دو نقطهای که به دست آوردیم را در دستگاه مختصات به هم وصل کرده و امتداد دهیم تا نمودار زیر حاصل شود:
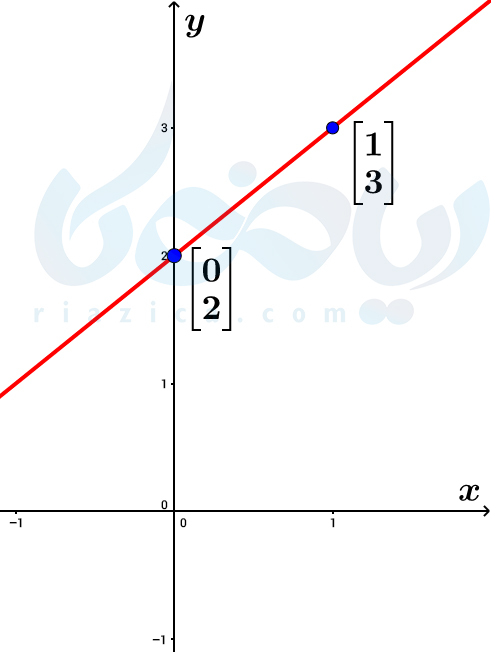
به مثال بعدی از درسنامۀ معادله خط ریاضی نهم توجه کنید.
مثال از رسم خط
مثال 2 معادله خط ریاضی نهم: خط به معادلۀ \(\Large y=-x+1\) را رسم کنید.
حل: مانند مثال قبل، کافی است دو نقطه پیدا کنیم که در معادلۀ بالا صدق کنند. اگر \(\Large x\) را برابر با \(\Large 1\) قرار دهیم، مقدار \(\Large y\) برابر با \(\Large 0\) خواهد شد. در نتیجه، نقطۀ \(\Large \begin{bmatrix} 1 \\ 0 \end{bmatrix}\) در معادلۀ بالا صدق میکند. به همین ترتیب، اگر \(\Large x\) را برابر با \(\Large 2\) قرار دهیم، مقدار \(\Large y\) برابر با \(\Large -1\) خواهد بود. بنابراین، نقطۀ \(\Large \begin{bmatrix} 2 \\ -1 \end{bmatrix}\) نیز در معادلۀ بالا صدق میکند. حال کافی است دو نقطهای که به دست آوردیم را در دستگاه مختصات به هم وصل کنیم تا نمودار زیر حاصل شود:
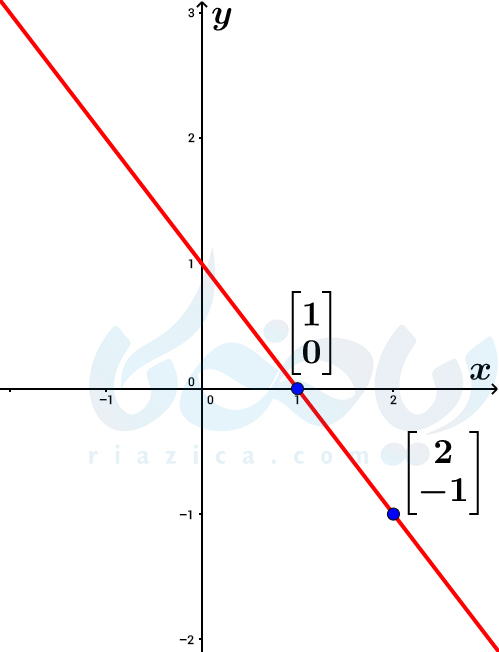
مثال از درسنامۀ معادله خط ریاضی نهم
مثال 3 معادله خط ریاضی نهم: مختصات محل برخورد خط به معادلۀ \(\Large y=\frac{1}{3}x-2 \) را با محورهای مختصات بیابید.
حل: نقطهای از خط که روی محور \(\Large y\) قرار داشته باشد، دارای طول صفر است. به عبارت دیگر، نقاط روی محور \(\Large y\) به شکل \(\Large \begin{bmatrix}0 \\ y \end{bmatrix}\) هستند. از طرفی نقطهای از خط که روی محور \(\Large x\) قرار داشته باشد، دارای عرض صفر است. به عبارت دیگر، نقاط روی محور \(\Large x\) به شکل \(\Large \begin{bmatrix} x \\ 0 \end{bmatrix}\) هستند. بنابراین، برای پیدا کردن خواستۀ مسئله، باید دو گام برداریم:
- برای پیدا کردن محل برخورد خط با محور \(\Large y\)، مقدار \(\Large x\) را در معادلۀ خط برابر با \(\Large 0\) قرار داده و مقدار \(\Large y\) را به دست میآوریم. محل برخورد به صورت \(\Large \begin{bmatrix} 0\\ y \end{bmatrix}\) خواهد شد.
- برای پیدا کردن محل برخورد خط با محور \(\Large x\)، مقدار \(\Large y\) را در معادلۀ خط برابر با \(\Large 0\) قرار داده و مقدار \(\Large x\) را به دست میآوریم. محل برخورد به صورت \(\Large \begin{bmatrix} x\\ 0 \end{bmatrix}\) خواهد شد.
بنابراین در گام اول، مقدار \(\Large x\) را در معادلۀ \(\Large y=\frac{1}{3}x-2 \) برابر با \(\Large 0\) قرار میدهیم. مقدار \(\Large y\) برابر با \(\Large -2\) میشود. پس، محل برخورد خط با محور \(\Large y\)، نقطۀ \(\Large \begin{bmatrix} 0\\ -2 \end{bmatrix}\) است.
در گام دوم، مقدار \(\Large y\) را در معادلۀ \(\Large y=\frac{1}{3}x-2 \) برابر با \(\Large 0\) قرار میدهیم. مقدار \(\Large x\) برابر با \(\Large 6\) میشود. پس، محل برخورد خط با محور \(\Large x\)، نقطۀ \(\Large \begin{bmatrix} 6\\ 0 \end{bmatrix}\) است.
در شکل زیر، خط \(\Large y=\frac{1}{3}x-2 \) را رسم کردیم تا روی نمودار نیز، محل برخورد با محورهای مختصات را مشاهده کنید.
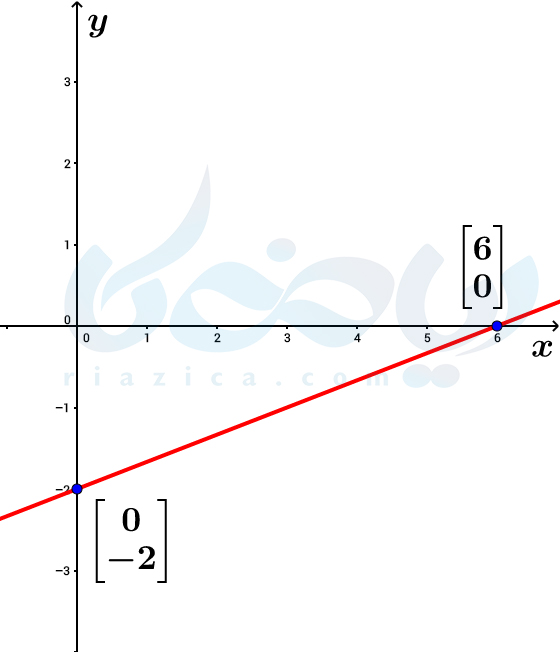
به قسمت بعدی از درسنامۀ معادله خط ریاضی نهم توجه کنید.
معادلۀ خط گذرنده از مبدأ
خطوطی به شکل \(\Large y=ax\) که در آن \(\Large a\) یک عدد حقیقی است، همیشه از مبدأ مختصات (یعنی نقطۀ \(\Large \begin{bmatrix} 0\\ 0 \end{bmatrix}\)) عبور میکنند. اما چرا؟ اگر مقدار \(\Large x\) را برابر با \(\Large 0\) قرار دهیم، مقدار \(\Large a\) هر چه باشد، \(\Large y\) برابر با \(\Large 0\) خواهد شد. بنابراین نقطۀ \(\Large \begin{bmatrix} 0\\ 0 \end{bmatrix}\) در تمام معادلات به شکل \(\Large y=ax\) صدق میکنند. پس تمامی این خطوط از مبدأ عبور میکنند. برای اینکه نمونهای از این خطوط را دیده باشید، به مثال بعدی از درسنامۀ معادله خط ریاضی نهم توجه کنید.
مثال از خط گذرنده از مبدأ
مثال 4 معادله خط ریاضی نهم: خط به معادلۀ \(\Large y=-\frac{2}{5}x\) را در نظر بگیرید. ابتدا مختصات نقطهای از این خط که دارای طول \(\Large 5\) است را پیدا کرده و سپس خط را رسم کنید.
حل: همان طور که گفتیم، خطوطی به شکل \(\Large y=ax\) از مبدأ مختصات عبور میکنند. در اینجا \(\Large a=-\frac{2}{5}\) است. برای پیدا کردن مختصات نقطهای از این خط که دارای طول \(\Large 5\) است، باید مقدار \(\Large x\) را برابر با \(\Large 5\) قرار داده و مقدار \(\Large y\) را به دست آوریم. اگر این کار را انجام دهیم، مقدار \(\Large y\) برابر با \(\Large -2\) خواهد شد. در نتیجه، نقطۀ \(\Large \begin{bmatrix} 5\\ -2 \end{bmatrix}\) دارای طول \(\Large 5\) بوده و روی خط قرار دارد.
از آنجاییکه خط از مبدأ عبور میکند و همچنین نقطۀ \(\Large \begin{bmatrix} 5\\ -2 \end{bmatrix}\) نیز روی خط قرار دارد، برای رسم خط کافی است مبدأ را به نقطۀ \(\Large \begin{bmatrix} 5\\ -2 \end{bmatrix}\) وصل کرده و امتداد دهیم:
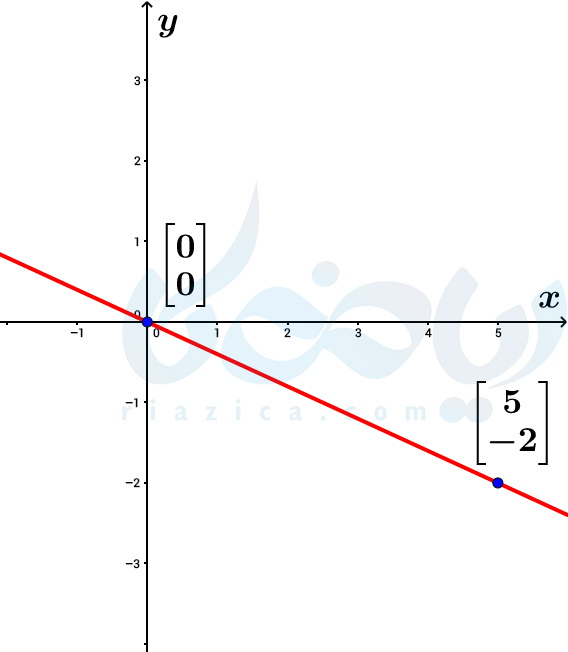
برای یادگیری مطالب بیشتر در این زمینه به درسنامه آموزش معادله خط مراجعه کنید.
زنگ آخر کلاس معادله خط ریاضی نهم
در درسنامهای که از ریاضی نهم خواندیم، ابتدا رابطۀ بین دو متغیر را بررسی کردیم. سپس، برخی از جوابهای یک معادلۀ دو متغیره را به دست آوردیم. همان طور که دیدید، جوابهای آن معادلۀ خاص، روی یک خط واقع میشد. در ادامه، با معادلۀ خط آشنا شدیم. روش رسم یک خط از روی معادلۀ آن را بررسی کردیم و دیدیم در چه صورتی یک خط از مبدأ عبور میکند.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با معادله خط ریاضی نهم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





عالییییییی
با سلام وعرض ادب
ممنون از نظر لطف شما
دمتون گرم واقعا.قشنگ متوجه شدم?❤
با سلام و سپاس فراوان مطالبتان بسیار عالی و مرتب و دقیق و سنجیده نوشته شده اند .
با سلام وادب
ممنون دوست عزیز تیم ما برای نوشتن مطالب وقت ودقت زیادی صرف کرده
عالی?
سلام به شما خیلی ممنون مطالب عالی بود
در امتحان آمده بود که معادله خطی که از دو نقطه (3-*2-)و(3-*1+)میگذرد حساب کنید. من اول با فرمول خواستم شیب رو حساب کنم(تفاضل عرض ها و تفاضل ایکس ها )که شیب 0 شد و نمیدونم چطور معادله خط رو باید می نوشتم اگر امکانش هست راهنمایی کنید
با سلام وادب
خطوطی که شیب آنها صفر است موازی محور ایکسها هستن که به صورت y=b هست که b عرض نقطه مورد نقاط مورد نظر هست که در این مثال -3 هست
عالی
با سلام و ادب
ممنون
ممنون واقعاعالی بوذ
سلام دوست عزیز
ممنون از محبت شما
کامل وجامع