آموزش ریاضی پایه دوازدهم تجربی
تانژانت ⭕️✖️ – آموزش با تصویر
در این درسنامه به مبحث تانژانت میپردازیم. ابتدا تانژانت را روی دایره مثلثاتی خواهیم دید. سپس، در مورد تغییراتش در ربعهای مختلف بحث خواهیم کرد. در ادامه نیز، تابع تانژانت و رسم آن را بررسی میکنیم.
تانژانت در دایره مثلثاتی
دایره مثلثاتی که در شکل زیر رسم شده است را در نظر بیرید. \(\Large tan\) زاویۀ \(\Large \alpha\) برابر است با نسبت ضلع مقابل به مجاور. یعنی \(\Large \frac{AB}{OA}\). از طرفی همان طور که میدانید، شعاع دایره مثلثاتی، واحد است. یعنی \(\Large OA=1\). در نتیجه \(\Large tan\) زاویۀ \(\Large \alpha\) برابر است با \(\Large AB\).
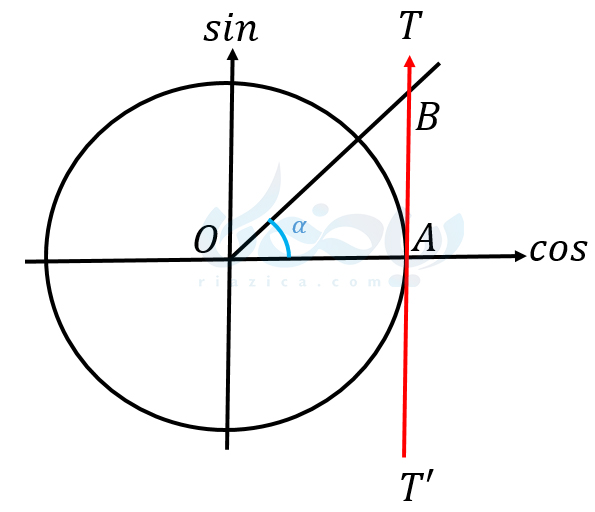
پس اگر بخواهیم مانند سینوس و کسینوس، برای تانژانت نیز یک محور تعریف کنیم، میتوانیم مانند شکل بالا خط موازی با محور سینوس که بر دایره مماس است و در ربع اول و چهارم مختصات قرار دارد، یعنی خط \(\Large TAT’\) را محور تانژانت بنامیم. نقطۀ \(\Large A\) مبدأ محور تانژانت است. جهت این محور نیز مانند جهت محور سینوس است.
پیدا کردن زاویهای با تانژانت دلخواه
اگر عددی مانند \(\Large x\) روی محور تانژانت داشته باشیم و بخواهیم زاویهای مانند \(\Large \alpha\) پیدا کنیم به طوری که \(\Large \tan \alpha=x\)، باید چه کار کنیم؟ شکل زیر را در نظر بگیرید. اگر از نقطۀ \(\Large x\) روی محور تانژانت نیمخطی رسم کنیم که از مبدا مختصات عبور کند، دایره مثلثاتی را در دو نقطۀ \(\Large m\) و \(\Large n\) قطع خواهد کرد. همان طور که میبینید، نقطۀ \(\Large m\) متناظر با زاویۀ \(\Large \alpha\) و نقطۀ \(\Large n\) متناظر با زاویۀ \(\Large \alpha + \pi\) است.
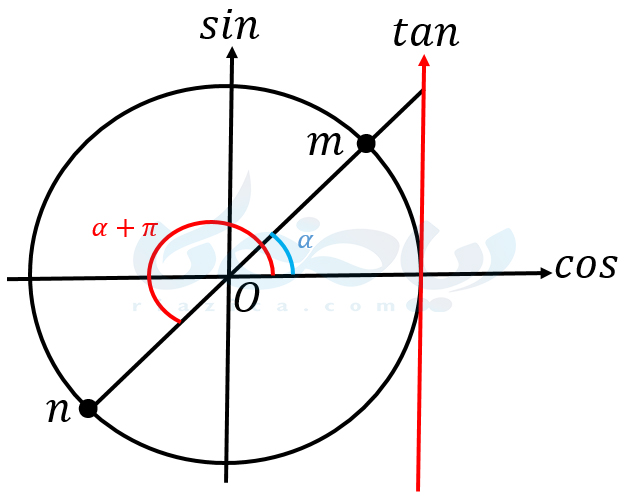
اگر مقدار \(\Large \pi\) رادیان به زاویۀ \(\Large \alpha\) اضافه کنیم، از نقطۀ \(\Large m\) به نقطۀ \(\Large n\) میرسیم و اگر یک \(\Large \pi\) رادیان دیگر ادامه دهیم به نقطۀ \(\Large m\) روی دایره مثلثاتی بر خواهیم گشت. یعنی علاوه بر زاویۀ \(\Large \alpha\) که \(\Large tan\) آن برابر با \(\Large x\) است، اگر تعدادی \(\Large \pi\) رادیان به \(\Large \alpha\) اضافه یا از آن کم کنیم، \(\Large tan\) زاویۀ حاصل نیز برابر با \(\Large x\) خواهد بود. بنابراین میتوانیم بنویسیم:
\(\Large \tan (\alpha \pm k\pi)=x\)
تغییرات تانژانت
در این قسمت قصد داریم تغییرات \(\Large tan\) را در ربعهای مختلف بررسی کنیم.
ربع اول
برای بررسی تغییرات \(\Large tan\) در ربع اول، زاویۀ \(\Large \alpha\) را از \(\Large 0\) تا \(\Large \frac{\pi}{2}\) افزایش داده و تغییرات \(\Large \tan \alpha\) را بررسی میکنیم. همانطور که در شکل زیر مشخص است، تانژانت \(\Large \alpha\) به ازای \(\Large \alpha=0\) برابر با \(\Large 0\) است. در زاویۀ \(\Large \frac{\pi}{2}\)، خط گذرنده از مبدأ، با محور تانژانت موازی است و آن را در هیچ نقطهای قطع نمیکند. اما اگر زاویه را افزایش داده و به آرامی \(\Large \alpha\) را به \(\Large \frac{\pi}{2}\) نزدیک کنیم، میبینیم که مقدار \(\Large tan\) مرتباً افزایش مییابد. در نتیجه با میل \(\Large \alpha\) به \(\Large \frac{\pi}{2}\)، مقدار \(\Large \tan \alpha\) به \(\Large +\infty\) میل میکند. به عنوان جمع بندی میتوان گفت مقدار تانژانت در ربع اول از صفر تا مثبت بینهایت افزایش مییابد.
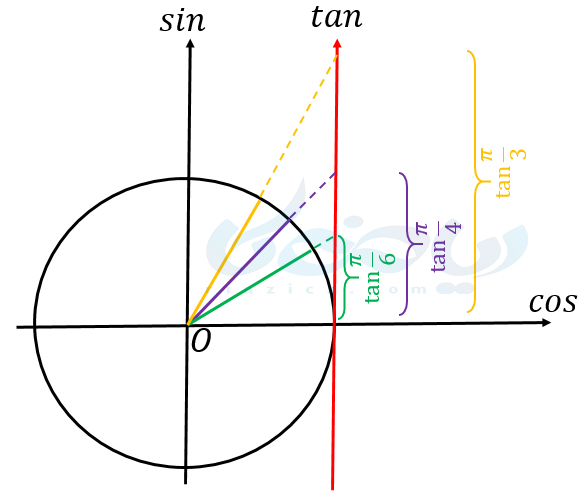
در ادامه \(\Large \tan \alpha\) را برای سه زاویۀ مهم در ربع اول به دست میآوریم:
\(\Large \tan \frac{\pi}{6}=\frac{\sin \frac{\pi}{6}}{\cos \frac{\pi}{6}}=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}=\frac{\sqrt{3}}{3}\)
\(\Large \tan \frac{\pi}{4}=\frac{\sin \frac{\pi}{4}}{\cos \frac{\pi}{4}}=\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}=1\)
\(\Large \tan \frac{\pi}{3}=\frac{\sin \frac{\pi}{3}}{\cos \frac{\pi}{3}}=\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}=\sqrt{3}\)
ربع دوم
در ربع دوم، زاویۀ \(\Large \alpha\) از \(\Large \frac{\pi}{2}\) تا \(\Large \pi\) افزایش پیدا میکند. در \(\Large \alpha=\frac{\pi}{2}\)، خط گذرنده از مبدأ، محور تانژانت را در هیچ نقطهای قطع نمیکند. اما اگر \(\Large \alpha\) را از \(\Large \frac{\pi}{2}\) به تدرج افزایش دهیم، مقدار \(\Large \tan \alpha\) از \(\Large -\infty\) شروع به افزایش میکند. در زاویۀ \(\Large \pi\)، مقدار \(\Large tan\) برابر با صفر است. در نتیجه میتوانیم بگوییم \(\Large \tan \alpha\) در ربع دوم از \(\Large -\infty\) تا \(\Large 0\) افزایش پیدا میکند. در شکل زیر میتوانید تغییرات \(\Large tan\) را در ربع دوم مشاهده کنید.
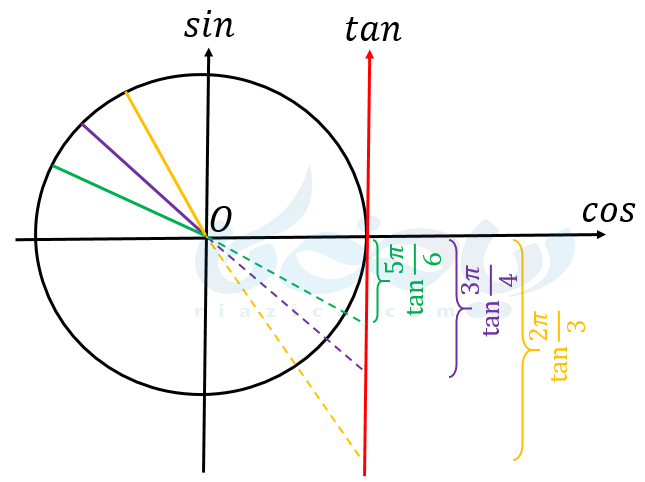
در ادامه، \(\Large \tan \alpha\) را برای سه زاویۀ مهم در ربع دوم به دست میآوریم:
\(\Large \tan \frac{2\pi}{3}=\frac{\sin \frac{2\pi}{3}}{\cos \frac{2\pi}{3}}=\frac{\frac{\sqrt{3}}{2}}{\frac{-1}{2}}=-\sqrt{3}\)
\(\Large \tan \frac{3\pi}{4}=\frac{\sin \frac{3\pi}{4}}{\cos \frac{3\pi}{4}}=\frac{\frac{\sqrt{2}}{2}}{-\frac{\sqrt{2}}{2}}=-1\)
\(\Large \tan \frac{5\pi}{6}=\frac{\sin \frac{5\pi}{6}}{\cos \frac{5\pi}{6}}=\frac{\frac{1}{2}}{-\frac{\sqrt{3}}{2}}=-\frac{\sqrt{3}}{3}\)
ربع سوم
در ربع سوم، زاویۀ \(\Large \alpha\) از \(\Large \pi\) تا \(\Large \frac{3\pi}{2}\) افزایش پیدا میکند. در زاویهء \(\Large \pi\)، مقدار \(\Large tan\) برابر با صفر است. در \(\Large \alpha=\frac{3\pi}{2}\)، خط گذرنده از مبدأ، محور تانژانت را در هیچ نقطهای قطع نمیکند. اما اگر \(\Large \alpha\) را به تدریج به \(\Large \frac{3\pi}{2}\) نزدیک کنیم، مقدار \(\Large \tan \alpha\) به \(\Large +\infty\) میل میکند. در نتیجه میتوانیم بگوییم \(\Large \tan \alpha\) در ربع سوم از \(\Large 0\) تا \(\Large +\infty\) افزایش پیدا میکند. در شکل زیر میتوانید تغییرات تانژانت را در ربع سوم مشاهده کنید.
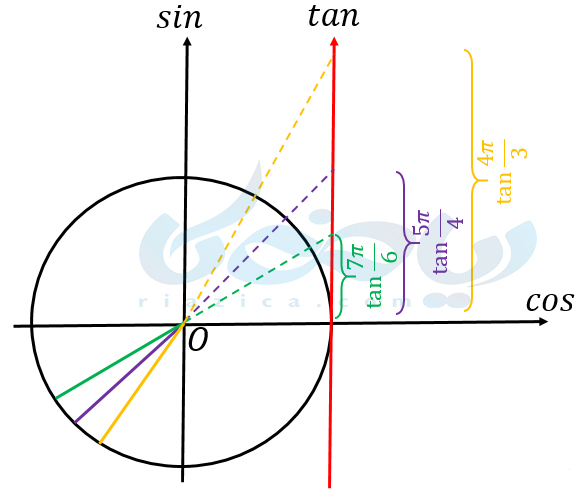
در ادامه \(\Large \tan \alpha\) را برای سه زاویۀ مهم در ربع سوم به دست میآوریم:
\(\Large \tan \frac{7\pi}{6}=\frac{\sin \frac{7\pi}{6}}{\cos \frac{7\pi}{6}}=\frac{\frac{-1}{2}}{\frac{-\sqrt{3}}{2}}=\frac{\sqrt{3}}{3}\)
\(\Large \tan \frac{5\pi}{4}=\frac{\sin \frac{5\pi}{4}}{\cos \frac{5\pi}{4}}=\frac{-\frac{\sqrt{2}}{2}}{-\frac{\sqrt{2}}{2}}=1\)
\(\Large \tan \frac{4\pi}{3}=\frac{\sin \frac{4\pi}{3}}{\cos \frac{4\pi}{3}}=\frac{\frac{-\sqrt{3}}{2}}{\frac{-1}{2}}=\sqrt{3}\)
ربع چهارم
در ربع چهارم، زاویهء \(\Large \alpha\) از \(\Large \frac{3\pi}{2}\) تا \(\Large 2\pi\) افزایش پیدا میکند. در \(\Large \alpha=\frac{3\pi}{2}\)، خط گذرنده از مبدأ، محور تانژانت را در هیچ نقطهای قطع نمیکند. اما اگر \(\Large \alpha\) را از \(\Large \frac{3\pi}{2}\) به تدرج افزایش دهیم، مقدار \(\Large \tan \alpha\) از \(\Large -\infty\) شروع به افزایش میکند. در زاویهء \(\Large 2\pi\)، مقدار \(\Large tan\) برابر با صفر است. در نتیجه میتوانیم بگوییم \(\Large \tan \alpha\) در ربع چهارم از \(\Large -\infty\) تا \(\Large 0\) افزایش پیدا میکند. در شکل زیر میتوانید تغییرات \(\Large tan\) را در ربع چهارم مشاهده کنید.
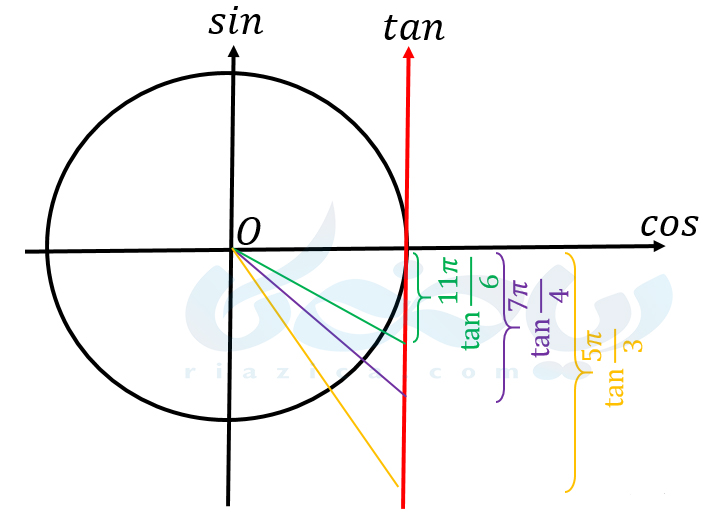
در ادامه، \(\Large \tan \alpha\) را برای سه زاویهء مهم در ربع چهارم به دست میآوریم:
\(\Large \tan \frac{5\pi}{3} = \frac{\sin \frac{5\pi}{3}}{\cos \frac{5\pi}{3}}=\frac{\frac{-\sqrt{3}}{2}}{\frac{1}{2}}=-\sqrt{3}\)
\(\Large \tan \frac{7\pi}{4} = \frac{\sin \frac{7\pi}{4}}{\cos \frac{7\pi}{4}}=\frac{-\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}=-1\)
\(\Large \tan \frac{11\pi}{6}=\frac{\sin \frac{11\pi}{6}}{\cos \frac{11\pi}{6}}=\frac{-\frac{1}{2}}{\frac{\sqrt{3}}{2}}=-\frac{\sqrt{3}}{3}\)
تابع تانژانت
برای اینکه به تانژانت به عنوان یک تابع نگاه کنیم، کافی است دامنه و برد آن را مشخص کنیم. به غیر از زوایای \(\Large k\pi+\frac{\pi}{2}\) که \(\Large k\) یک عدد صحیح است، \(\Large tan\) زوایای دیگر وجود داشته و متناهی است. توجه کنید، از آنجاییکه \(\Large +\infty\) و \(\Large -\infty\)، اعداد حقیقی نیستند، نمیتوانیم بگوییم تانژانت زوایای \(\Large k\pi+\frac{\pi}{2}\) وجود دارند. بنابراین دامنۀ تابع \(\Large f(x)=\tan x\) برابر است با مجموعۀ:
\(\Large D=\{x \in \mathbb{R} | x \neq k\pi+\frac{\pi}{2}, k\in \mathbb{Z}\}\)
زمانی که تغییرات تانژانت را در ربعهای اول تا چهارم بررسی کردیم، دیدم که \(\Large \tan x\) از \(\Large -\infty\) تا \(\Large +\infty\) تغییر میکند. بنابراین برد تابع \(\Large f(x)=\tan x\) برابر است با مجموعۀ اعداد حقیقی.
دوره تناوب تابع تانژانت
در ابتدای درسنامه گفتیم که اگر تعدادی \(\Large \pi\) رادیان به \(\Large \alpha\) اضافه یا از آن کم کنیم، \(\Large tan\) زاویۀ حاصل تغییری نخواهد کرد. یعنی داریم:
\(\Large \tan (x \pm k\pi)=tan(x)\)
بنابراین طبق تعریف دوره تناوب، دوره تناوب تابع تانژانت برابر است با \(\Large \pi\).
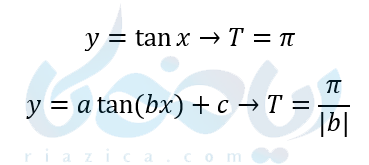
رسم تابع \(\Large tan\)
اگر تابع تانژانت را در بازۀ \(\Large [-\frac{3\pi}{2}, \frac{3\pi}{2}]\) رسم کنیم، شکل زیر به دست میآید.
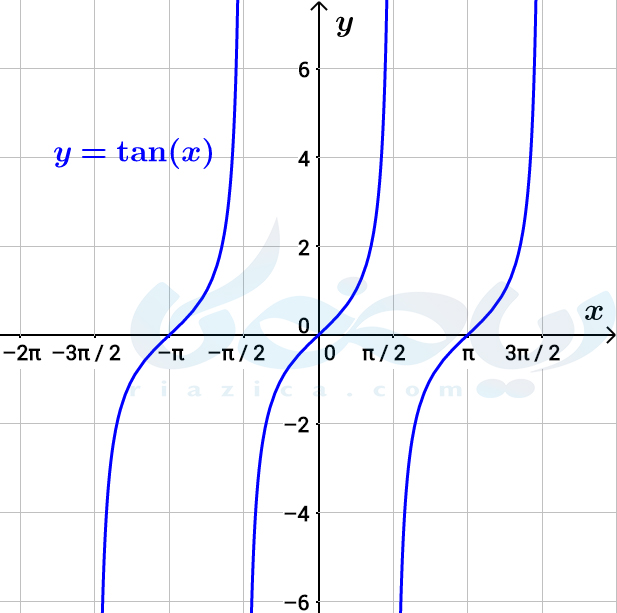
از آنجاییکه تابع متناوب است، نمودار تابع با تناوب \(\Large \pi\) تکرار میشود. همانطور که میبنید، تابع تانژانت در برخی از بازهها مثل بازۀ \(\Large (-\frac{\pi}{2}, \frac{\pi}{2})\)، اکیداً صعودی است، اما در مجموعۀ اعداد حقیقی نه صعودی است، نه نزولی. برای اینکه بهتر متوجه شوید، مقدار تابع تانژانت را در سه نقطه به دست میآوریم:
\(\Large \tan (x=\frac{\pi}{3})=\sqrt{3}\)
\(\Large \tan (x=\pi)=0\)
\(\Large \tan (x=\frac{4\pi}{3})=\sqrt{3}\)
همانطور که میبینید، \(\Large \pi\) بزرگتر از \(\Large \frac{\pi}{3}\) است، اما \(\Large 0\) از \(\Large \sqrt{3}\) کوچکتر است. از طرفی \(\Large \frac{4\pi}{3}\) بزرگتر از \(\Large \pi\) است، \(\Large \sqrt{3}\) نیز از \(\Large 0\) بزرگتراست. بنابراین، در مورد یکنوایی تابع تانژانت میتوان گفت این تابع در دامنۀ خود، نه صعودی است و نه نزولی.
مثال از مقایسۀ تانژانت و سینوس
مثال 1: مقادیر تابع سینوس را با تابع تانژانت در ربعهای مختلف مقایسه کنید.
حل: در ربع دوم، مقادیر تابع سینوس مثبت و مقادیر تابع تانژانت منفی است. بنابراین سینوس یک زاویه از تانژانت آن در ربع دوم بیشتر است. در ربع سوم نیز، مقادیر تابع سینوس منفی و تانژانت مثبت است. بنابراین، \(\Large tan\) یک زاویه از سینوس آن در ربع سوم بیشتر است. در ربع اول، هم سینوس و هم تانژانت مثبت هستند. از آنجاییکه \(\Large tan\) از تقسیم سینوس بر کسینوس به دست میآید و مقدار کسینوس در این ربع، عددی بین صفر و یک است، بنابراین تانژانت یک زاویه در این ربع مقداری بیشتر از سینوس آن دارد. در شکل زیر نیز میتوانید این موضوع را به صورت شهودی برای یک زاویه در ربع اول مشاهده کنید.
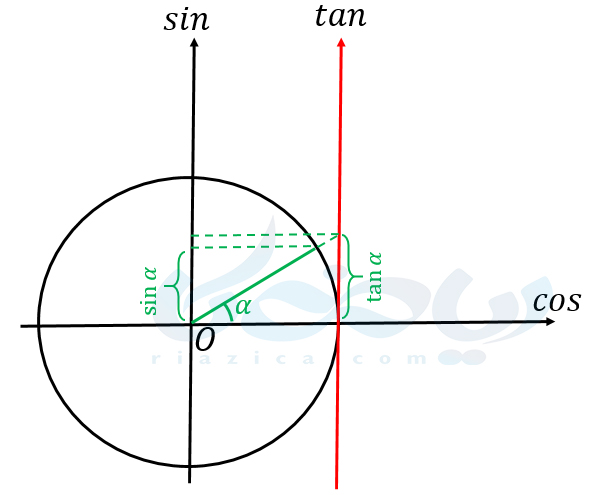
در ربع چهارم، هم سینوس و هم \(\Large tan\) یک زاویه منفی است. اگر مقادیر نسبتهای مثلثاتی را بدون علامتشان در نظر بگیریم، باز هم مانند ربع اول، تانژانت یک زاویه مقداری بیشتر از سینوس آن خواهد داشت. از آنجاییکه هم علامت سینوس و هم تانژانت منفی است، پس \(\Large tan\) یک زاویه از سینوس آن کوچکتر است. در شکل زیر نیز میتوانید این موضوع را به صورت شهودی برای یک زاویه در ربع چهارم مشاهده کنید.
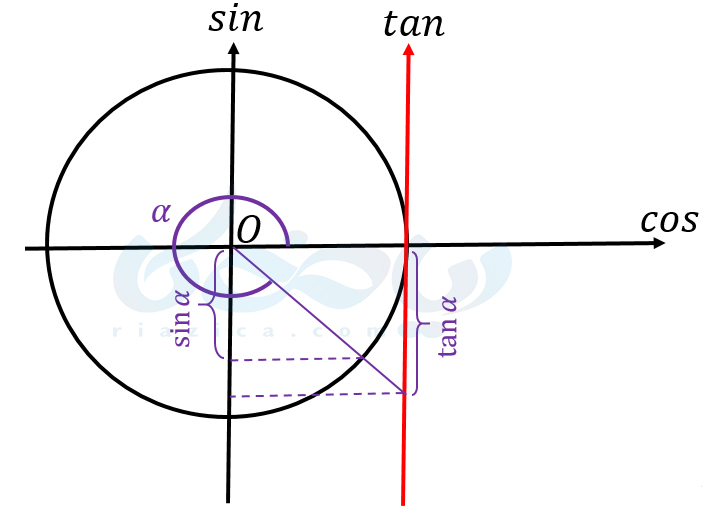
پس به طور کلی داریم:

زنگ آخر کلاس \(\Large tan\)
در این درسنامه که مربوط به ریاضی دوازدهم تجربی بود، نسبت مثلثاتی تانژانت را بررسی کردیم. در مورد تغییرات \(\Large tan\) در ربعهای اول تا چهارم صحبت کردیم. همانطور که دیدید میتوانیم به تانژانت به شکل یک تابع نیز نگاه کنیم. دامنه و برد تابع تانژانت را مشخص کرده و نمودار آن را رسم کردیم. نشان دادیم که تابع تانژانت در دامنۀ خود نه صعودی است و نه نزولی. علاوه بر این، دیدیم که تابع تانژانت ، متناوب بوده و دورۀ تناوب آن برابر با \(\Large \pi\) است.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث تانژانت دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





واقعا؟
با سلام
تعجب شما بابت چیه؟
بسیار عالی ممنونم
سلام ممنون از نگاه شما
ممنون از توصیحات کاملتون
با سلام ممنون از نگاه شما
با سلام بسیار ممنونم من کاملا متوجه شدم
با سلام وادب
خوشحالیم که مفید واقع شده